《视觉SLAM十四讲》-- 相机与图像
04 相机与图像
4.1 相机模型
4.1.1 针孔相机模型
针孔模型描述了一束光线通过针孔后,在针孔背面投影成像的关系(类似小孔成像原理)。
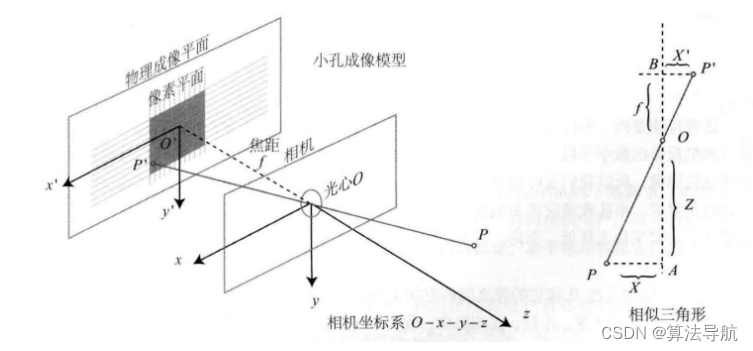
根据相似三角关系
Z f = − X X ′ = − Y Y ′ (3-1) \frac{Z}{f}=-\frac{X}{X^{\prime}}=-\frac{Y}{Y^{\prime}} \tag{3-1} fZ=−X′X=−Y′Y(3-1)
其中,负号表示成的像是倒立的。
但实际相机得到的图像并不是倒像,我们等价地将成像平面对称地放到相机前方,这样就可以把负号去掉,
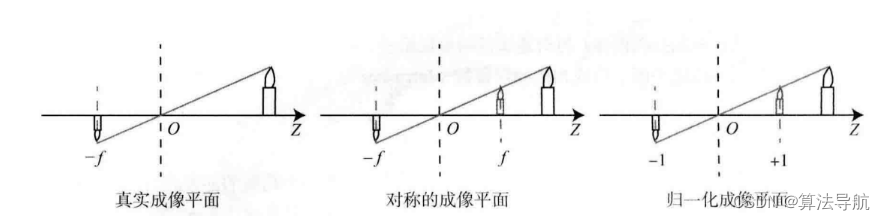
Z f = X X ′ = Y Y ′ (3-2) \frac{Z}{f}=\frac{X}{X^{\prime}}=\frac{Y}{Y^{\prime}} \tag{3-2} fZ=X′X=Y′Y(3-2)
整理得
{ X ′ = f X Z Y ′ = f Y Z (3-3) \left\{\begin{array}{l} {X^{\prime}}=f\frac{X}{Z} \\ \\ {Y^{\prime}}=f\frac{Y}{Z} \end{array}\right. \tag{3-3} ⎩ ⎨ ⎧X′=fZXY′=fZY(3-3)
像素坐标与成像平面之间,相差了一个缩放和一个原点的平移。假设像素坐标在 u u u 轴上缩放了 α \alpha α 倍, 在 v v v 轴上缩放了 β \beta β 倍,同时,原点平移了 [ c x , c y ] T [c_x, c_y]^T [cx,cy]T。那么, P ′ P' P′ 在成像平面坐标系和像素坐标系之间的关系为:
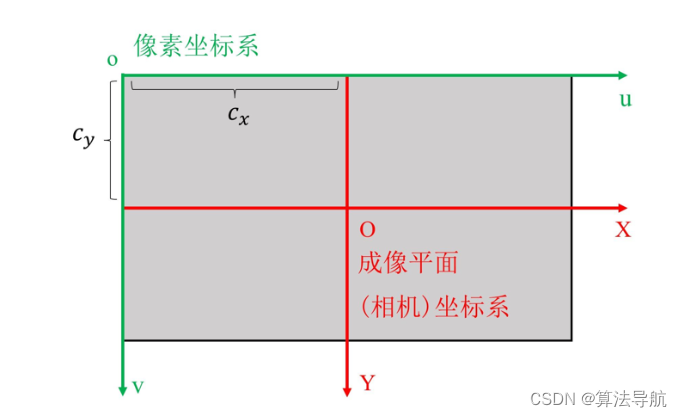
{ u = α X ′ + c x v = β Y ′ + c y (3-4) \left\{\begin{array}{l} u=\alpha X^{\prime}+c_{x} \\ v=\beta Y^{\prime}+c_{y} \end{array}\right. \tag{3-4} {u=αX′+cxv=βY′+cy(3-4)
代入式(3-3),得
{ u = α f X Z + c x v = β f Y Z + c y (3-5) \left\{\begin{array}{l} u=\alpha f \frac{X}{Z}+c_{x} \\ \\ v=\beta f \frac{Y}{Z}+c_{y} \end{array}\right. \tag{3-5} ⎩ ⎨ ⎧u=αfZX+cxv=βfZY+cy(3-5)
记 α f = f x , \alpha f=f_x, αf=fx,, β f = f y \beta f=f_y βf=fy 得
{ u = f x X Z + c x v = f y Y Z + c y (3-6) \left\{\begin{array}{l} u=f_{x} \frac{X}{Z}+c_{x} \\ \\ v=f_{y} \frac{Y}{Z}+c_{y} \end{array}\right. \tag{3-6} ⎩ ⎨ ⎧u=fxZX+cxv=fyZY+cy(3-6)
写成矩阵形式
[ u v 1 ] = 1 Z [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] = def 1 Z K P (3-7) \left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\frac{1}{Z}\left[\begin{array}{ccc} f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} X \\ Y \\ Z \end{array}\right] \stackrel{\text { def }}{=} \frac{1}{Z} \boldsymbol{K} \boldsymbol{P} \tag{3-7} uv1 =Z1 fx000fy0cxcy1 XYZ = def Z1KP(3-7)
将 Z Z Z 移到左边
Z [ u v 1 ] = [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] = def K P (3-8) Z\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\left[\begin{array}{ccc} f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} X \\ Y \\ Z \end{array}\right] \stackrel{\text { def }}{=} \boldsymbol{K} \boldsymbol{P} \tag{3-8} Z uv1 = fx000fy0cxcy1 XYZ = def KP(3-8)
中间的矩阵称为相机内参数,一般在相机出厂后便已确定。
由于相机在运动,点 P P P 的相机坐标应由他的世界坐标( P w P_w Pw)根据相机当前位姿变换得到
Z P u v = Z [ u v 1 ] = K P = K ( R P w + t ) = K T P w (3-9) Z \boldsymbol{P}_{u v}=Z\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\boldsymbol{K} \boldsymbol{P}=\boldsymbol{K}\left(\boldsymbol{R} \boldsymbol{P}_{\mathrm{w}}+\boldsymbol{t}\right)=\boldsymbol{K} \boldsymbol{T} \boldsymbol{P}_{\mathrm{w}} \tag{3-9} ZPuv=Z uv1 =KP=K(RPw+t)=KTPw(3-9)
其中, R \boldsymbol{R} R、 t \boldsymbol{t} t 为外参。
上式描述了从世界坐标系到相机坐标系再到像素坐标系的过程。
将世界坐标转换到相机坐标后,再除掉最后一维的数值,这相当于把最后一维作归一化处理,得到它在归一化平面上的投影:
( R P w + t ) = [ X , Y , Z ] T ⏟ 相机坐标 → [ X / Z , Y / Z , 1 ] T ⏟ 归一化坐标 \left(\boldsymbol{R} \boldsymbol{P}_{\mathrm{w}}+\boldsymbol{t}\right)=\underbrace{[X, Y, Z]^{\mathrm{T}}}_{\text {相机坐标 }} \rightarrow \underbrace{[X / Z, Y / Z, 1]^{\mathrm{T}}}_{\text {归一化坐标 }} (RPw+t)=相机坐标 [X,Y,Z]T→归一化坐标 [X/Z,Y/Z,1]T
可知,点的深度信息在投影过程中丢失了(变成二维),所以单目视觉无法得到像素点深度值。
4.1.2 畸变模型
(1)由透镜形状引起的畸变称为径向畸变,一般有桶形畸变和枕形畸变两类。
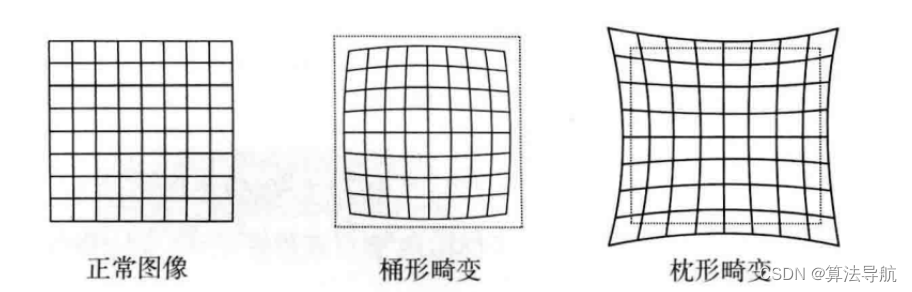
对于径向畸变,离中心距离越远,畸变越严重;穿过图像中心和光轴有交点的直线形状不变。
(2)在相机组装过程中,透镜和成像平面无法完全平行,会产生切向畸变。
(3)下面用数学模型进行描述:假设归一化平面上存在一点 P P P,坐标为 [ x , y ] T [x, y]^T [x,y]T,极坐标为 [ r , θ ] T [r, \theta]^T [r,θ]T,那么,正常归一化平面坐标和畸变后的坐标之间的关系为
{ x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) (3-10) \left\{\begin{array}{l} x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)\\ \\ y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6) \end{array}\right. \tag{3-10} ⎩ ⎨ ⎧xdistorted=x(1+k1r2+k2r4+k3r6)ydistorted=y(1+k1r2+k2r4+k3r6)(3-10)
类似的,切向畸变数学模型为
{ x distorted = x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y distorted = y + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y (3-11) \left\{\begin{array}{l} \begin{aligned} &x_{\text {distorted }}=x+2 p_{1} x y+p_{2}\left(r^{2}+2 x^{2}\right) \\ &y_{\text {distorted }}=y+p_{1}\left(r^{2}+2 y^{2}\right)+2 p_{2} x y \end{aligned} \end{array}\right. \tag{3-11} {xdistorted =x+2p1xy+p2(r2+2x2)ydistorted =y+p1(r2+2y2)+2p2xy(3-11)
(4)去畸变的过程:
-
将三维空间上的点投影到归一化平面,得到坐标 [ x , y ] T [x, y]^T [x,y]T;
-
计算径向畸变和切向畸变
{ x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y (3-12) \left\{\begin{array}{l} x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)+2 p_{1} x y+p_{2}\left(r^{2}+2 x^{2}\right)\\ \\ y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6)+p_{1}\left(r^{2}+2 y^{2}\right)+2 p_{2} x y \end{array}\right. \tag{3-12} ⎩ ⎨ ⎧xdistorted=x(1+k1r2+k2r4+k3r6)+2p1xy+p2(r2+2x2)ydistorted=y(1+k1r2+k2r4+k3r6)+p1(r2+2y2)+2p2xy(3-12)
- 通过内参矩阵将相机坐标投影到像素平面。
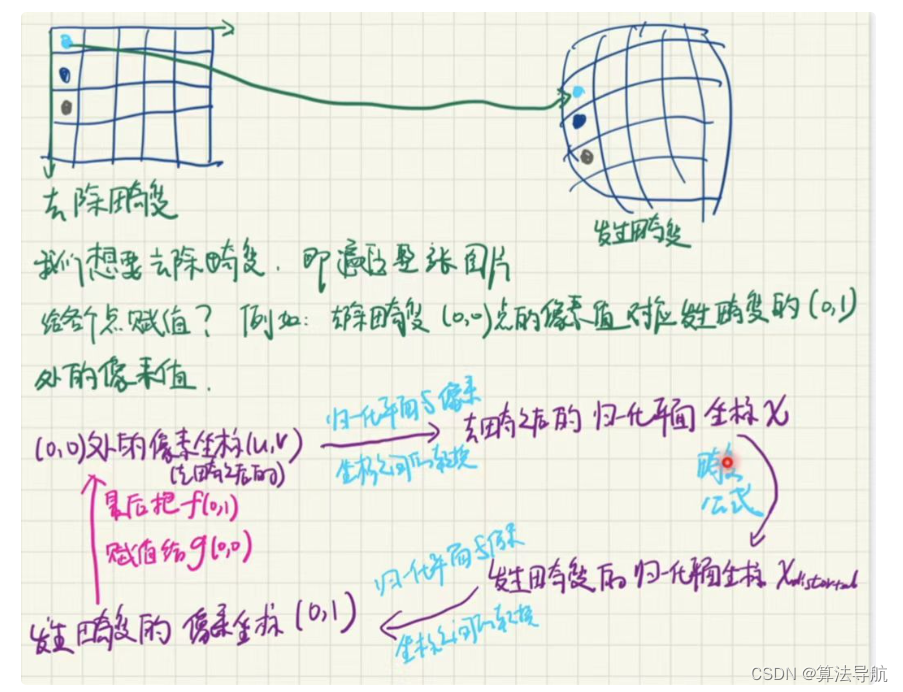
(5)单目相机的成像过程
-
世界坐标系下一点 P w P_w Pw;
-
经旋转平移得到相机坐标 P ~ c = R P w + t \tilde{P}_{\mathrm{c}}=\boldsymbol{RP_w+t} P~c=RPw+t;
-
将坐标的三个分量分别除以 Z Z Z,得到归一化坐标 P c = [ X / Z , Y / Z , 1 ] T P_c=[X/Z, Y/Z, 1]^T Pc=[X/Z,Y/Z,1]T;
-
计算发生畸变后的坐标;
-
经过内参矩阵,得到像素坐标 P u v = K P c \boldsymbol{P}_{uv}=\boldsymbol{KP_c} Puv=KPc。
4.1.3 双目相机模型
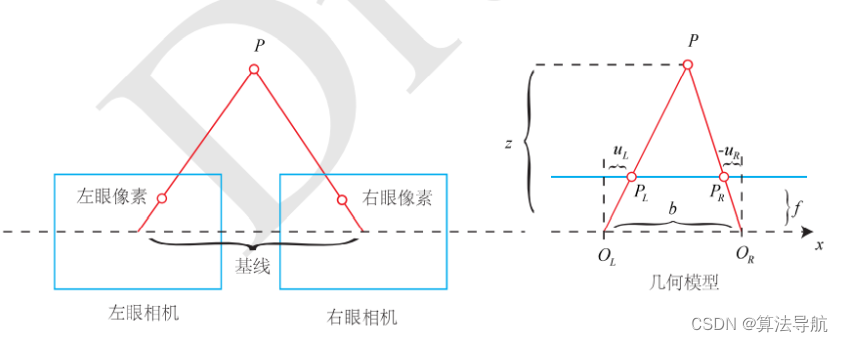
其中, O L O_L OL 和 O R O_R OR为左右相机光圈中心,两者之间的距离称为基线; f f f 为焦距; u R u_R uR 为负数,需加负号。
根据几何关系,有
z − f z = b − ( u L − u R ) b = b − u L + u R b (3-13) \frac {z-f}{z}=\frac {b-(u_L-u_R)} {b}=\frac {b-u_L+u_R} {b} \tag{3-13} zz−f=bb−(uL−uR)=bb−uL+uR(3-13)
定义 d = u L − u R d=u_L-u_R d=uL−uR,称为视差, 整理上式得,
z = f b d (3-14) z=\frac {fb}{d} \tag{3-14} z=dfb(3-14)
可见,视差越大,距离越近。基线 b b b 越大,可测量的距离就越大;反之,小型双目器件只能测量很近的距离。
4.1.4 RGB-D 相机模型
RGB-D 相机可以主动测量每个像素的深度,按原理可分为两类:
-
通过红外结构光原理测量像素距离。
-
通过飞行时间原理测量像素距离。
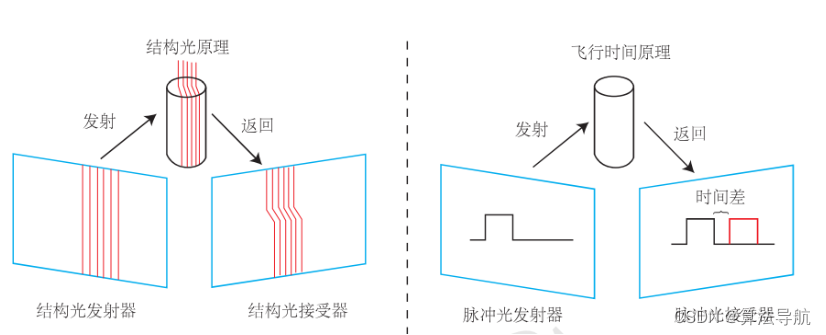
RGB-D 相机容易受到日光或其他传感器的干扰,因此不能在室外使用。
4.2 图像
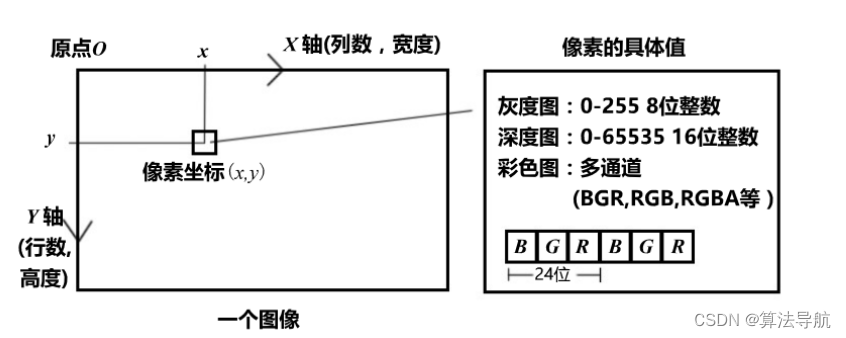
相关文章:

《视觉SLAM十四讲》-- 相机与图像
04 相机与图像 4.1 相机模型 4.1.1 针孔相机模型 针孔模型描述了一束光线通过针孔后,在针孔背面投影成像的关系(类似小孔成像原理)。 根据相似三角关系 Z f − X X ′ − Y Y ′ (3-1) \frac{Z}{f}-\frac{X}{X^{\prime}}-\frac{Y}{Y^{\p…...

欧科云链:成本与规模之辨——合规科技如何赋能香港Web3生态?
作为国际金融中心,香港近两年来在虚拟资产及Web3领域频频发力。秉持着“稳步创新”的基本逻辑,香港在虚拟资产与Web3领域已建立一定优势,但近期各类风险事件的发生则让业界的关注焦点再次转向“安全”与“合规”。 在香港FinTech Week前夕&a…...

【文献分享】NASA JPL团队CoSTAR一大力作:直接激光雷达里程计:利用密集点云快速定位
论文题目:Direct LiDAR Odometry: Fast Localization With Dense Point Clouds 中文题目:直接激光雷达里程计:利用密集点云快速定位 作者:Kenny Chen, Brett T.Lopez, Ali-akbar Agha-mohammadi 论文链接:https://arxiv.org/pd…...
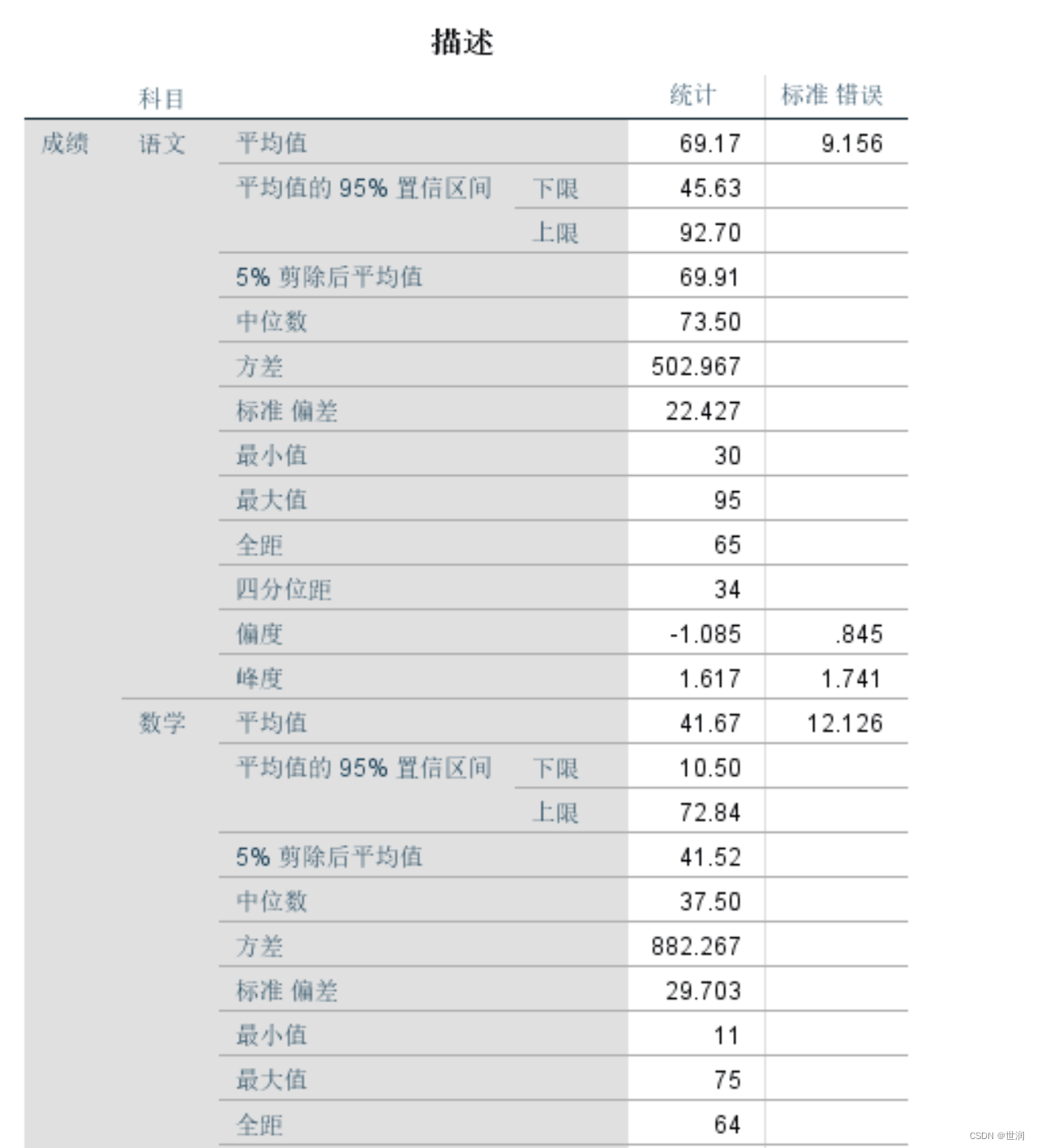
SPASS-探索性分析
探索性分析的意义 探索性分析更加强大,它是一种在对资料的性质、分布特点等完全不清楚的情况下,对变量进行更深入研究的描述性统计方法。在进行统计分析前,通常需要寻求和确定适合所研究的问题的统计方法, SPSS提供的探索性分析是解决此类问题的有效办法 探索性分析提供了很…...

电子印章怎么弄?三步教你电子印章在线生成免费教程!
在这个数字化快速发展的时代,电子印章已经成为日常商务活动中不可或缺的一部分。相对于传统的实体印章,电子印章具有更高的便捷性和安全性,更是无纸化办公中必不可少的一环。那么,电子印章怎么弄呢?跟着下面这三步来操…...

以技术创新引领行业发展,飞凌嵌入式获双项省级荣誉
近日,飞凌嵌入式荣获「2023年河北省专精特新示范企业」以及「第五批省级制造业单项冠军企业」两项殊荣。这两项荣誉的获得,是对飞凌嵌入式在专业技术领域与创新能力的高度认可,荣誉的背后,凝聚着飞凌嵌入式无数次的研发探索与对创…...

在Google Kubernetes集群创建分布式Jenkins(二)
上一篇博客在Google Kubernetes集群创建分布式Jenkins(一)-CSDN博客我介绍了如何在GCP的K8S集群上部署一个分布式的Jenkins,并实现了一个简单的Pipeline的运行。 在实际的开发中,我们通常都会按照以下的CICD流程来设置Pipeline 在我司的实际实践中&…...

GEE:GEE中调用 Math.js 教程
作者:CSDN @ _养乐多_ Math.js 是一个强大的 JavaScript 数学库,它提供了大量用于数学计算的函数和工具。这个库可用于解决各种数学问题,从基本的算术运算到高级数学和线性代数等领域。本文将介绍在 Google Earth Engine(GEE)云平台中调用 Math.js 第三方库做一些事情的方…...
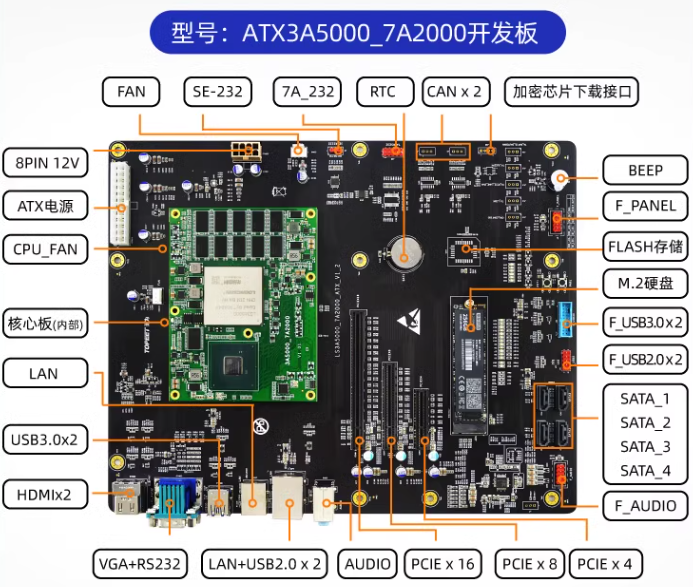
迅为龙芯3A5000主板,支持PCIE 3.0、USB 3.0和 SATA 3.0显示接口2 路、HDMI 和1路 VGA,可直连显示器
性能强 采用全国产龙芯3A5000处理器,基于龙芯自主指令系统 (LoongArch)的LA464微结构,并进一步提升频率,降低功耗,优化性能。 桥片 桥片采用龙芯 7A2000,支持PCIE 3.0、USB 3.0和 SATA 3.0显示接口2 路、HDMI 和1路 …...

Opencv for unity 下载
GitHub - EnoxSoftware/VideoPlayerWithOpenCVForUnityExample: This example shows how to convert VideoPlayer texture to OpenCV Mat using AsyncGPUReadback. OpenCV for Unity | Integration | Unity Asset Store...

独立IP主机怎么样?对网站有什么影响
对于现在企业来说,搭建网站是必不可少的,而大部分企业网站都会选择使用虚拟主机搭建,且使用的也是共享IP的这样会 有许多的弊端,所以部分站长会选择独立IP搭建。那么到底独立IP主机怎么样呢?使用独立IP主机搭建对网站有…...

Gerrit lfs安装及配置
Gerrit版本:3.1.4 lfs下载:Zuul Gerrit CI界面已经没有3.1.4对应版本的lfs.jar了,需要从上面的页面下载。 一、安装配置lfs 将上面下载的lfs.jar放到$GERRIT_SITE/plugins目录。 修改配置文件:$GERRIT_SITE/etc/gerrit.config …...
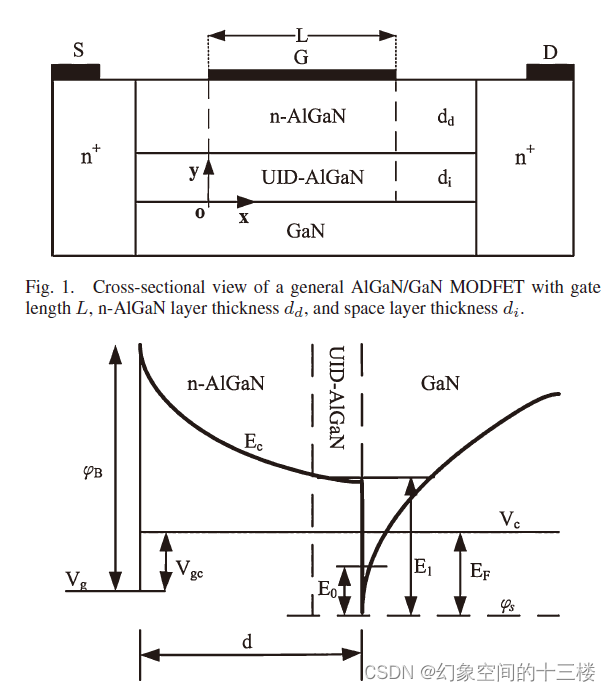
基于表面电势的AlGaN/GaN MODFET紧凑模型
标题:A Surface-Potential-Based Compact Model for AlGaN/GaN MODFETs 来源:IEEE TRANSACTIONS ON ELECTRON DEVICES(11年) 摘要 - 本文首次构建了基于表面势(SP)的AlGaN/GaN调制掺杂场效应晶体管&#…...

c语言中的fread
#include <stdio.h> //函数的定义: //size_t fread(void *ptr,size_t nmemb,FILE *stream); //函数的说明: //fread函数从stream所标示的文件中读取数据,一块是size个字节,共nmemb块,存放到ptr指向的内存里 …...

Unity游戏开发基础组件
Unity2D 相机调整:Projection设置为Orthographic。也就是正交模式,忽视距离。 资源: Sprite:一种游戏资源,在2D游戏中表示角色场景的图片资源 SpriteSheet:切割一张图片为多个Sprite 在Sprite Editor中可以…...

股票四倍杠杆什么意思?
股票四倍杠杆是指投资者通过借款或使用金融衍生品,以增加其投资股票的能力,达到放大投资回报的目的。具体来说,投资者可以通过向券商或银行等金融机构借入资金,或者使用融资融券等金融衍生品,以增加其购买股票的资本&a…...
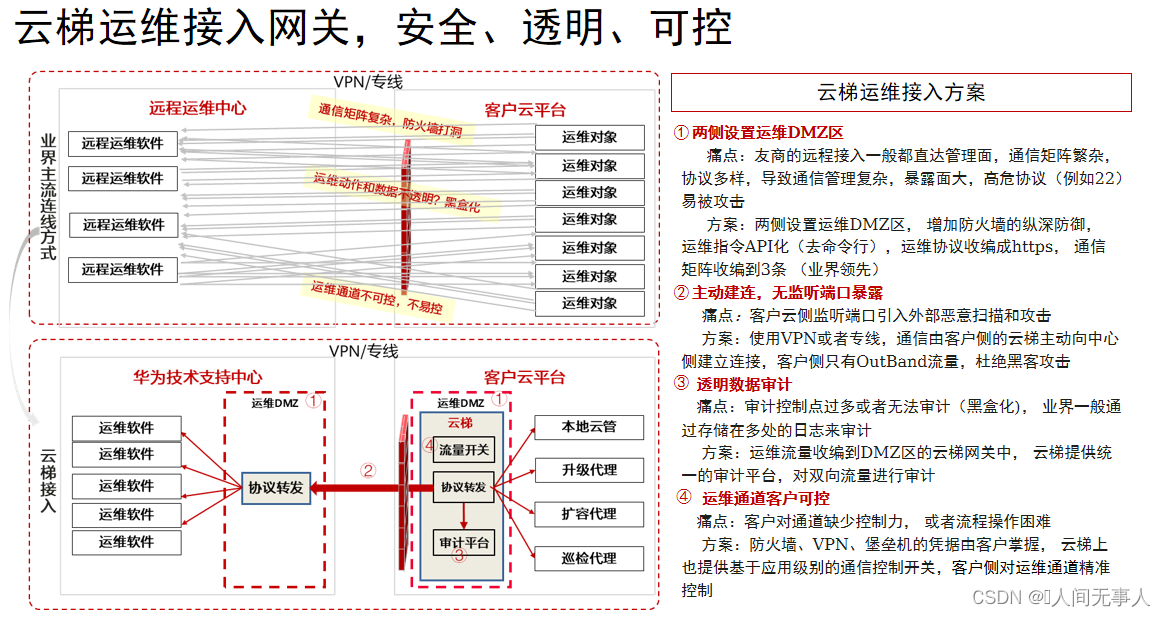
【hcie-cloud】【2】华为云Stack解决方案介绍、缩略语整理 【下】
文章目录 华为文档获取方式、云计算发展背景、坚实基座华为云Stack,政企只能升级首选智能数据湖仓一体,让业务洞见更准,价值兑现更快MRS:一个架构可构建三种数据湖,业务场景更丰富离线数据湖:提供云原生、湖…...

多无人机在线路径规划的新算法
南京航空航天大学自动化学院使用NOKOV度量动作捕捉系统获取多架无人机的精确位置信息,实现多架无人机协同实时路径规划。 研究背景 近年来,无人机越来越多地应用于执行战场侦察、目标识别、跟踪打击等任务。 由多架无人机协同执行任务,通过…...

什么是运营商精准大数据?又有什么作用?
大数据(big data),指无法在一定时间范围内用常规软件工具进行捕捉、管理和处理的数据集合,是需要新处理模式才能具有更强的决策力、洞察发现力和流程优化能力的海量、高增长率和多样化的信息资产。 精准大数据,是一种…...

Adobe Photoshop 2020给证件照换底
1.导入图片 2.用魔法棒点击图片 3.点选择,反选 4.选择,选择并遮住 5.用画笔修饰证件照边缘 6. 7.更换要换的底的颜色 8.新建图层 9.使用快捷键altdelete键填充颜色。 10.移动图层,完成换底。...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
