LeetCode题解:1238. 循环码排列,归纳法,详细注释
原题链接:
https://leetcode.cn/problems/circular-permutation-in-binary-representation/
前置条件:
- 在解题之前,请先一定要阅读89.格雷编码的题解
- 格雷编码可以满足题目的条件“
p[i]和p[i+1]的二进制表示形式只有一位不同”,以及“p[0]和p[2^n -1]的二进制表示形式也只有一位不同” - 我们需要将格雷编码转换成以
start开头的一串编码即可 - 为何要用异或:
- 格雷编码的第一个是
0,可以得知0 ^ start = start - 回顾一下异或操作,可以知道如果对每一位都进行异或操作,每一位之间的逻辑关系的变化是同步的
- 也就是说,
p[i]和p[i+1]的相互关系,以及p[0]和p[2^n -1]的相互关系不会改变
a | b | a XOR b
—|—|---------
0 | 0 | 0
0 | 1 | 1
1 | 0 | 1
1 | 1 | 0
- 格雷编码的第一个是
解法一:两次循环:
- 按照89.格雷编码的方法求出格雷编码
- 将格雷编码的每一位都按位异或
start,即可求得结果
/*** @param {number} n* @param {number} start* @return {number[]}*/
var circularPermutation = function (n, start) {/* * 第一步,先求格雷编码*/let result = [0] // 存储结果,第一个整数为0// 一共计算n位格雷码序列,需要循环n次for (let i = 0; i < n; i++) {// 每次计算时,已有的序列不变// 只需要计算已有序列的逆序列,每个再加前缀1// 需要缓存已有序列的长度,用于计算下一段序列const len = result.length// 由于是逆序计算,因此要从len - 1开始加前缀for (let j = len - 1; j >= 0; j--) {// 加前缀1后,把新值存入结果result.push(result[j] | (1 << i))}}/* * 第二步,将格雷编码的每一项都按位异或start*/for (let i = 0; i < result.length; i++) {result[i] ^= start}return result
}
解法二:
- 可以在解法一的基础上,将第二步的异或操作,放到第一步的第二层循环中,具体方法如下:
- 每次查找
result中的元素时,将其异或start,将其转为格雷编码 - 给格雷编码加上前缀
1 - 存入
result时,将其异或start,转为以start开头的编码
- 每次查找
/*** @param {number} n* @param {number} start* @return {number[]}*/
var circularPermutation = function (n, start) {let result = [start] // // 存储结果,第一个整数为start// 一共计算n位编码,需要循环n次for (let i = 0; i < n; i++) {// 每次计算时,已有的序列不变// 只需要计算已有序列的逆序列,每个再加前缀1// 需要缓存已有序列的长度,用于计算下一段序列const len = result.length// 由于是逆序计算,因此要从len - 1开始加前缀for (let j = len - 1; j >= 0; j--) {// 加前缀1后,把新值存入结果result.push(// 将编码异或start,转为格雷编码((result[j] ^ start) |// 为格雷编码加上前缀1(1 << i)) ^// 将格雷编码异或start,转为以start开头的编码start)}}return result
}
相关文章:

LeetCode题解:1238. 循环码排列,归纳法,详细注释
原题链接: https://leetcode.cn/problems/circular-permutation-in-binary-representation/ 前置条件: 在解题之前,请先一定要阅读89.格雷编码的题解格雷编码可以满足题目的条件“p[i] 和 p[i1] 的二进制表示形式只有一位不同”,…...

全新后门文件Nev-3.exe分析
一、 样本发现: 蜜罐 二、 内容简介: 通过公司的蜜罐告警发现一个Nev-3.exe可执行文件文件,对该样本文件进行分析发现,该可执行程序执行后会从远程服务器http://194.146.84.2:4395/下载一个名为“3”的压缩包,解压后…...

线性回归系数解释
线性回归系数解释线性回归系数1、R2R^2R2(R方,R-Square)2、Adj−R2Adj-R^2Adj−R2(调整后的 R 方)3、标准误差4、FFF 值5、FFF 显著度6、置信区间7、PPP 值线性回归系数 回归模型得到后会有多个系数,这些系…...
 A~D)
22.2.27打卡 Codeforces Round #852 (Div. 2) A~D
A Yet Another Promotion 题面翻译 题目描述 共 ttt 组数据,每组数据中,你需要买 nnn 公斤苹果,第一天单价为 aaa ,但每买 mmm 公斤赠送一公斤;第二天单价为 bbb 。求最小花费。 输入输出格式 第一行一个正整数 …...
如何查看Spring Boot各版本的变化
目录 1.版本 2.基础特性和使用 3.新增特性和Bug修复 1.版本 打开Spring官网,点进Spring Boot项目我们会发现在不同版本后面会跟着不同的标签: 这些标签对应不同的版本,其意思如下: GA正式版本,通常意味着该版本已…...

程序员是否要加入创业公司?
我从1月份入职到2月份离职,历时一个半月。短暂的体验了一段创业生活,更准确的说是一段“待在”创业团队的生活,因为我发现创业本身跟我关系不大。一个半月的就业经历,对任何人来说都不是一个好选择,当然也不是我所期望…...
2023软件测试工程师全新技术栈,吃透这些,起薪就是25k~
相信每个准备软件测试面试的同学,不管你是大学刚毕业,满心憧憬着进入公司实习、非计算机行业转行软件测试、自学测试就业还是培训后就业,都会面临着众多的疑问和不解,那就是该怎么走出着第一步,今天本文一次性告诉你&a…...

【ChatGPT情商大考验】ChatGPT教我谈恋爱
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...

C++类内存结构模型
内存分区 内存全局数据区,代码区,栈区,堆区。 定义一个类 类的成员函数被放在代码区 类的静态成员变量被放在全局数据区(不占用类的存储空间) 非静态成员在类的实例内,实例在栈区或者堆区 虚函数指针&…...
HTML#4超链接标签,列表标签,表格标签和布局标签
一. 超链接标签介绍<a> 定义超链接,用于连接到另一个资源herf: 指定访问资源的URLtarget: 指定打开资源的方式代码<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>超链接标签</title> <…...

本科课程【数字图像处理】实验汇总
文章目录 实验1 - 腐蚀与膨胀实验2 - 图像增强实验3 - 图像的几何变换实验4 - 图像的蒙纱效果实验5 - 空洞填充实验6 - 取阈值的邻域平均算法实验7 - 图像的平移与伸缩变换实验1 - 腐蚀与膨胀 实验目的 分析掌握腐蚀与膨胀的基本原理,编写腐蚀与膨胀的算法,并掌握开闭运算的规…...

nginx安装lua、jwt模块,通过lua验证jwt实现蓝绿发布样例
文章目录前言一、基础组件下载二、组件安装1.luajit安装2.lua-nginx-module安装3.lua-resty-core安装4.lua-resty-lrucache安装5.ngx_devel_kit安装6.nginx加载lua模块7.lua-cjson安装8.lua-resty-string安装9.lua-resty-jwt安装10.lua-resty-hmac安装三、验证jwt中属性实现蓝绿…...

【redis的几种数据结构及在Java里的应用案例】
Redis是一款高性能的key-value存储系统,支持多种数据结构,包括字符串、列表、哈希表、集合和有序集合等。下面是Redis的几种数据结构及在Java中的应用案例: string 字符串(String) 字符串是Redis中最基本的数据类型,用于存储字符…...

【mybatis】 01- mybatis快速入门
数据库创建(注意:最好先创建好数据库设置utf8再进行表创建) create database mybatis; use mybatis;drop table if exists tb_user;create table tb_user(id int primary key auto_increment,username varchar(20),password varchar(20),gender char(1),addr varch…...

【C语言每日一题】杨氏矩阵(源码以及改进源码)
【C语言每日一题】—— 杨氏矩阵😎😎😎 目录 💡前言🌞: 💛杨氏矩阵题目💛 💪 解题思路的分享💪 😊题目源码的分享😊 Ǵ…...

JavaScript 面向对象【快速掌握知识点】
目录 类和对象 属性和方法 继承 多态 封装 类和对象 类是用于定义对象的模板或蓝图;它包含对象的属性和方法,我们可以使用class关键字来定义类。 class Person {constructor(name, age) {this.name name;this.age age;}sayHello() {console.log(H…...
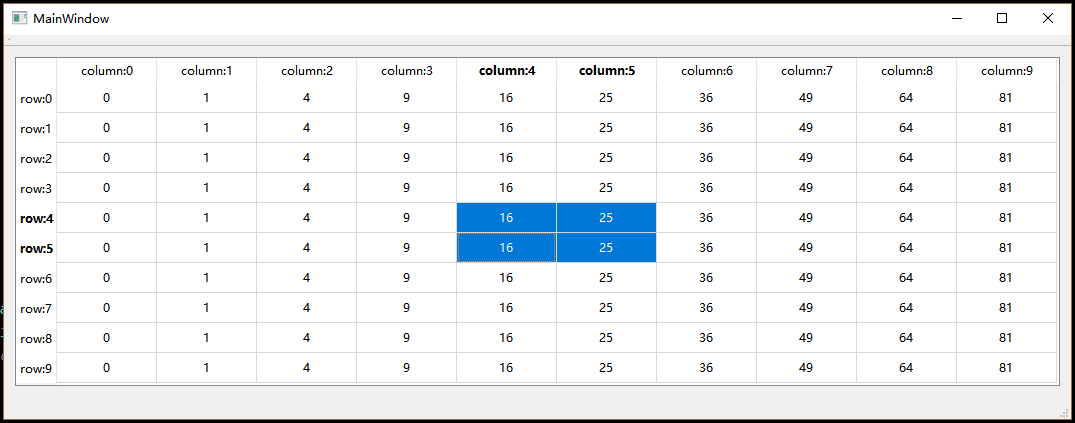
Qt——自定义Model
众所周知,Qt提供了一套Model/View框架供开发者使用,Model用来提供数据, View则用来提供视觉层的显示。实际上这是一套遵循MVC设计模式的GUI框架,因为Qt还提供了默认的Delegate作为Controller来作为控制器。 MVC的好处这里就不多说…...

用 .NET 启动你的 DJI Ryze Tello 无人机
大疆的 DJI Ryze Tello 是入门级的无人机,不仅在 STEM 教育中有非常广泛的应用,也可以作为编程入门的首选。通过 UDP 协议调用 DJI Ryze Tello SDK 可以让 DJI Ryze Tello 无人机执行起飞,降落,转向以及不同的花式动作。本文将会通…...
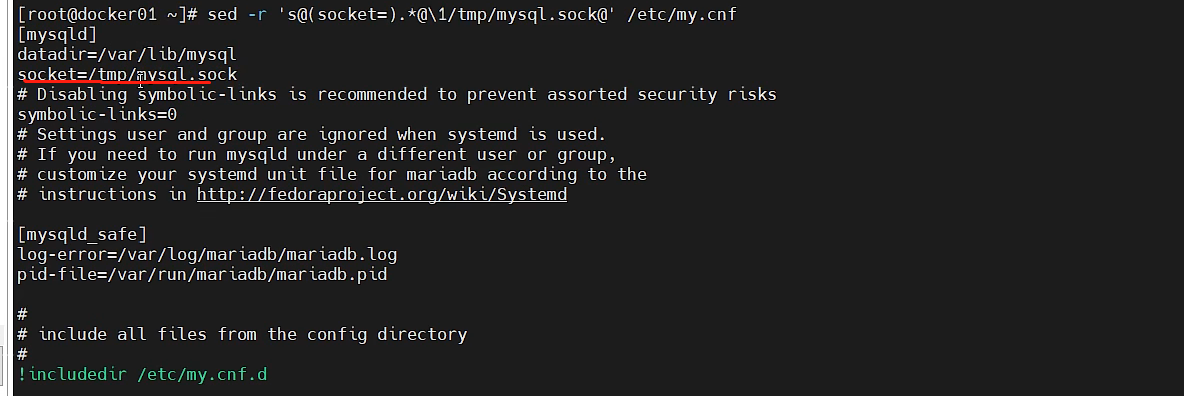
sed 功能详解
介绍sedsed是一种流编辑器,它一次处理一行内容,把当前处理的行存储在临时缓冲区中(buffer),称为"模式空间",接着sed命令处理缓冲区中的内容,处理完成后,把缓冲区的内容送往屏幕&#…...

整数二分思路详解
题目描述 给定一个按照升序排列的长度为n的整数数组,以及 q 个查询。 对于每个查询,返回一个元素k的起始位置和终止位置(位置从0开始计数)。 如果数组中不存在该元素,则返回“-1 -1”。 输入格式 第一行包含整数n和q&a…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
