万物皆数——用matlab求解二阶微分方程
一、背景
毕达哥拉斯的“万物皆数”哲学观点表达了一个理念,即宇宙万物都可以通过数学语言来描述,数是万物的本原。
勾股定理就是毕达哥拉斯提出,因此在西方勾股定理也被叫做毕达哥拉斯定理。
工科类的专业,越到后面越感觉到数学的重要性,无论是控制,计算机还是机器人专业,都需要很好的数学功底。
最近在做DMP相关的内容时,需要求解二阶微分方程,无奈早已把学的还给老师,可惜当时高数白考九十多分。但很感谢当时的高数老师于朝霞教授,讲课讲的真好,所以重新翻看高等数学第六版同济大学编著的微分方程章节时,很快捡起来之前学到的内容。
现在有了matlab,不需要自己手算了,下面记录一下使用matlab求解二阶微分方程的过程。
Matlab版本:2023a
二、Matlab求解二阶常系数微分方程
1、问题描述
二阶常系数微分方程:
y ¨ + 10 y ˙ + 25 y = 250 (1) \begin{aligned} \ddot y+10\dot y+25y=250 \\ \end{aligned}\tag{1} y¨+10y˙+25y=250(1)
二阶微分方程如果没有初始条件,其通解会含有两个任意常数,所以不能完全反应某一客观实物的规律。
这里设置初始条件为:
y ( 0 ) = 15 , y ˙ ( 0 ) = 0 (2) \begin{aligned} y(0)=15, &&\dot y(0)=0 \\ \end{aligned}\tag{2} y(0)=15,y˙(0)=0(2)
2、matlab求解微分方程,并绘制解的曲线
clear; close all; clc;
% 定义符号变量
syms x y(x);% 定义二阶微分方程
eqn = diff(y, x, 2) + 10*diff(y, x) + 25*y == 250;% 设置初始条件
initial_condition1 = y(0) == 0; % 初始值 y(0) = 0
initial_condition2 = subs(diff(y), 0) == 0; % 初始导数值 y'(0) = 0% 求解微分方程
sol = dsolve(eqn, [initial_condition1, initial_condition2]);% 显示解
disp('解:');
disp(sol);% 将解转换为函数句柄
ySol = matlabFunction(sol);% 定义 x 范围
x = linspace(0, 5, 100); % 这里的范围可以根据需要调整% 计算对应的 y 值
y = ySol(x);% 绘制曲线图
figure;
a1 = subplot( 1, 1, 1 );
hold( a1, 'on' );
plot(a1, x, y, 'linewidth', 3, 'color', [0.0000, 0.4470, 0.7410] );
xlabel('x');
ylabel('y');
title('二阶微分方程的解曲线');
scatter( 0, ySol(0), 'filled', 'linewidth', 3, 'markerfacecolor', 'y', 'markeredgecolor', 'k' );
grid on;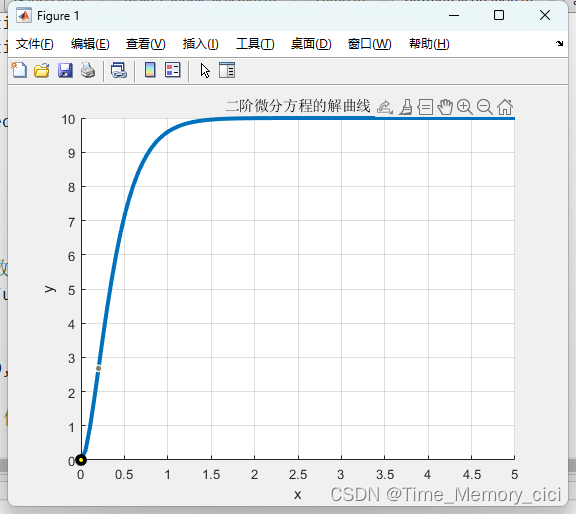
3、matlab求解加速度函数,并绘制解的曲线
经过步骤2,其实我们得到的是位置和速度的关系,即解为:
y = − 10 e − 5 x − 50 x e − 5 x + 10 (2) \begin{aligned} y=-10e^{-5x}-50xe^{-5x}+10 \\ \end{aligned}\tag{2} y=−10e−5x−50xe−5x+10(2)
有时我们还需要观察加速度和时间的关系。
因此对公式(2)求二阶导,得到加速度:
y ¨ = 250 e − 5 x − 1250 x e − 5 x (2) \begin{aligned} \ddot y=250e^{-5x}-1250xe^{-5x} \\ \end{aligned}\tag{2} y¨=250e−5x−1250xe−5x(2)
matlab里求解加速度与时间的关系,及画出曲线图:
clear; close all; clc;
% 定义符号变量
syms x;% 定义函数
y = 10 - 50*x*exp(-5*x) - 10*exp(-5*x);% 计算二阶导数
second_derivative = diff(y, x, 2);
% 显示解
disp('二阶导:');
disp(second_derivative);
% 将二阶导数转换为函数句柄
second_derivative_func = matlabFunction(second_derivative);% 定义 x 范围
x_values = linspace(0, 5, 100); % 这里的范围可以根据需要调整% 计算对应的二阶导数值
y_second_derivative = second_derivative_func(x_values);% 绘制二阶导数曲线图
figure;
plot(x_values, y_second_derivative);
xlabel('x');
ylabel('y的二阶导数');
title('y=5*exp(-5*x) + 25*x*exp(-5*x) + 10 的二阶导数曲线');
grid on;
相关文章:

万物皆数——用matlab求解二阶微分方程
一、背景 毕达哥拉斯的“万物皆数”哲学观点表达了一个理念,即宇宙万物都可以通过数学语言来描述,数是万物的本原。 勾股定理就是毕达哥拉斯提出,因此在西方勾股定理也被叫做毕达哥拉斯定理。 工科类的专业,越到后面越感觉到数学…...
jmeter接口自动化部署jenkins教程
首先,保证本地安装并部署了jenkins,jmeter,xslproc 我搭建的自动化测试框架是jmeterjenkinsxslproc ---注意:原理是,jmeter自生成的报告jtl文件,通过xslproc工具,再结合jmeter自带的模板修改&…...

前端js实现将数组对象组装成自己需要的属性,或者去掉对象中不必要的属性
前言 提示:这里可以添加本文要记录的大概内容: 需求:前端js实现将数组对象组装成自己需要的属性,或者前端js实现去掉对象中不必要的属性 提示:以下是本篇文章正文内容,下面案例可供参考 一、示例数组对象…...
MeterSphere 任意文件读取漏洞(CVE-2023-25814)
MeterSphere 任意文件读取漏洞(CVE-2023-25814) 免责声明漏洞描述漏洞影响漏洞危害网络测绘Fofa: title"MeterSphere" 漏洞复现1. 构造poc2. 发送数据包3. 查看文件 免责声明 仅用于技术交流,目的是向相关安全人员展示漏洞利用方式,以便更好地…...

设计模式-01-单例设计模式
经典的设计模式有23种,但是常用的设计模式一般情况下不会到一半,我们就针对一些常用的设计模式进行一些详细的讲解和分析,方便大家更加容易理解和使用设计模式。 1-为什么要使用单例 单例设计模式(Singleton Design Pattern&…...
霍尔电流传感器如何进行可靠性测试?主要应用在哪些领域?
霍尔电流传感器广泛应用于航空航天、电源监测、飞行器状态监测、变速驱动设备、焊接设备供电电源、新能源汽车蓄电池管理系统等领域,在电流检测领域中有着重要地位和实用价值,在电驱系统中被称为新能源汽车的动力“心脏”。因此,霍尔电流传感…...

pandas按行按列遍历Dataframe的三种方式
遍历数据有以下三种方法: 简单对上面三种方法进行说明: iterrows(): 按行遍历,将DataFrame的每一行迭代为(index, Series)对,可以通过row[name]对元素进行访问。 itertuples(): 按行遍历,将DataFrame的每一行迭代为元…...

Api接口如何防止被刷?
现在越来越多的应用程序和服务都提供了API接口,使得开发人员可以方便地与这些应用程序和服务进行交互。但是,由于API接口是公开的,因此很容易被黑客利用,对系统造成损害。为了确保API接口的安全性,我们需要采取一些措施…...
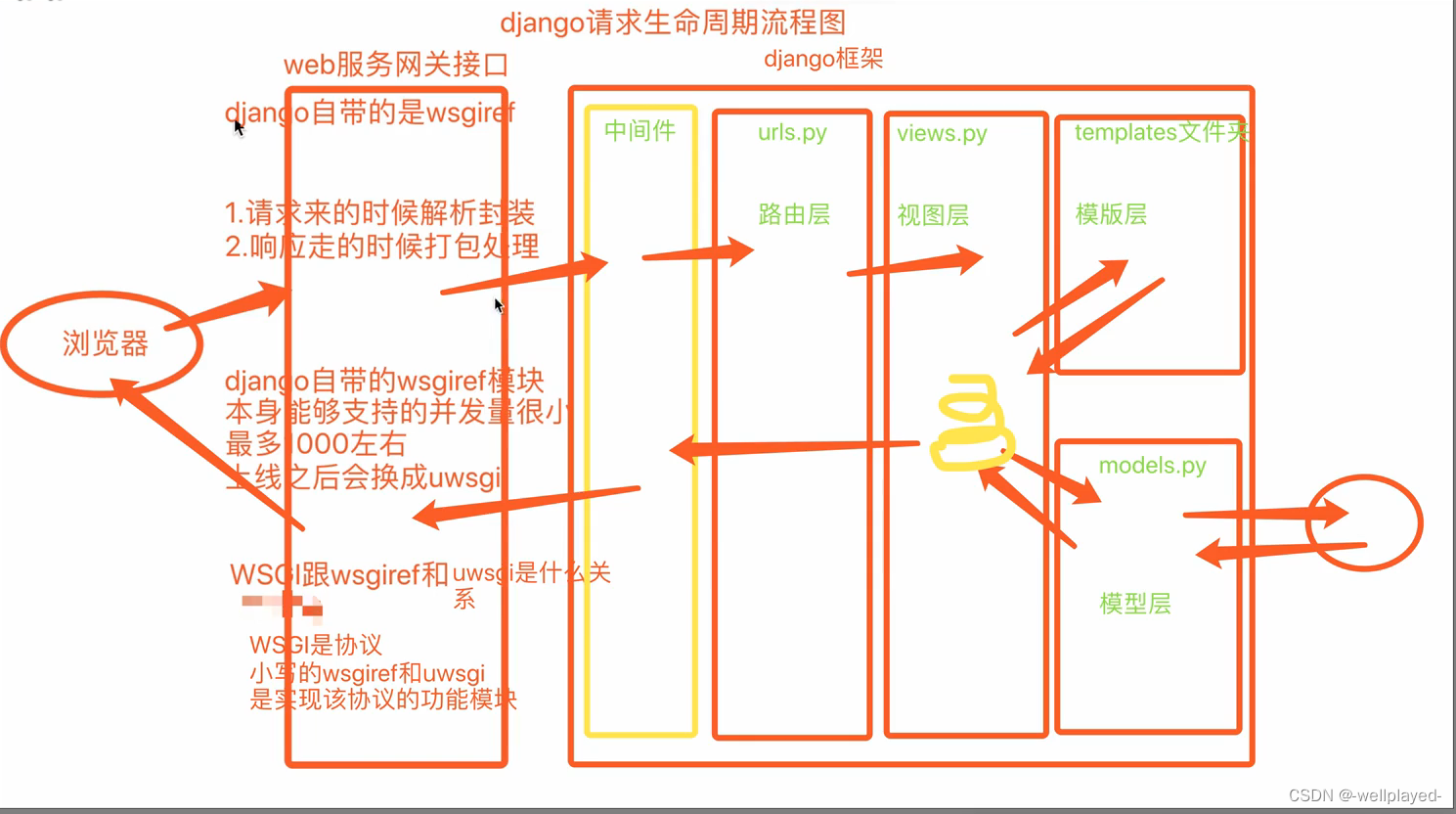
Django——orm模块创建表关系
django orm中如何创建表关系 1. 表关系分析 表与表之间的关系: 一对多 多对多 一对一 没有关系 判断表关系的方法: 换位思考用4张表举例: 图书表 出版社表 作者表 作者详情表图书和出版社是一对多的关系 外键字段建在多的那一方图书和作者是多对多的关系 需要创建第三张表来…...

Django知识点
目录 一、三板斧的使用 二、全局配置文件 三、静态文件的设置 四、request对象的方法 五、pycharm链接数据库 六、Django链接数据库 七、orm介绍 一、三板斧的使用 三个方法: HttpResponse renderredirect def index(request):print(request)return HttpR…...

基于单片机设计的智能风扇(红外线无线控制开关调速定时)
一、项目介绍 在炎热的夏季,风扇成为人们室内生活中必不可少的电器产品。然而,传统的风扇控制方式存在一些不便之处,比如需要手动操作开关、无法远程控制和调速,以及缺乏定时功能等。为了解决这些问题,设计了一款基于…...

k8s报错pause 3.2 解决方案
报错 Failed to create pod sandbox: rpc error: code Unknown desc failed to get sandbox image "k8s.gcr.io/pause:3.2": failed to pull image "k8s.gcr.io/pause:3.2": failed to pull and unpack image "k8s.gcr.io/pause:3.2": failed…...

基于遗传算法的电器分类,基于GA的电器分类
目录 背影 遗传算法的原理及步骤 基本定义 编码方式 适应度函数 运算过程 代码 结果分析 展望 完整代码下载链接:基于遗传算法的电器识别,基于遗传算法的电器分类(代码完整,数据齐全)资源-CSDN文库 https://download.csdn.net/download/abc991835105/88506649 背影 电器…...
某XX自考小程序的AES加密分析
前言 主要是报了自考在这个小程序上面做题,就研究了一下这个接口本文仅供学习交流使用,请勿随意传播。如有侵犯你的权益及时联系我删除。 一、抓包分析打开小程序,打开devtools 工具,这里就不啰嗦,直接上过程。 点击…...

加密算法笔记
MD5: 目前相对容易破解,且容易发生碰撞; 不可逆(但是网络上有很多破解方法) SHA256: 不会碰撞; 可以加盐,也可以不加盐; 不可逆; HmacSHA256在线加密-HmacMD5加密-散列哈希HASH加密工具 相同点 1、都是密码散列函数,加密不可逆。 2、都可…...

Sa-Token拦截全部接口必须登录-然后自定义注解来匿名登录-作为权限框架支持,并且同时使用了注解和路由的拦截器模式,此部分的配置如下:
场景 在博主目前正在开发的项目中,就采用了Sa-Token作为权限框架支持,并且同时使用了注解和路由的拦截器模式,此部分的配置如下: Override public void addInterceptors(InterceptorRegistry registry) { List<String> n…...
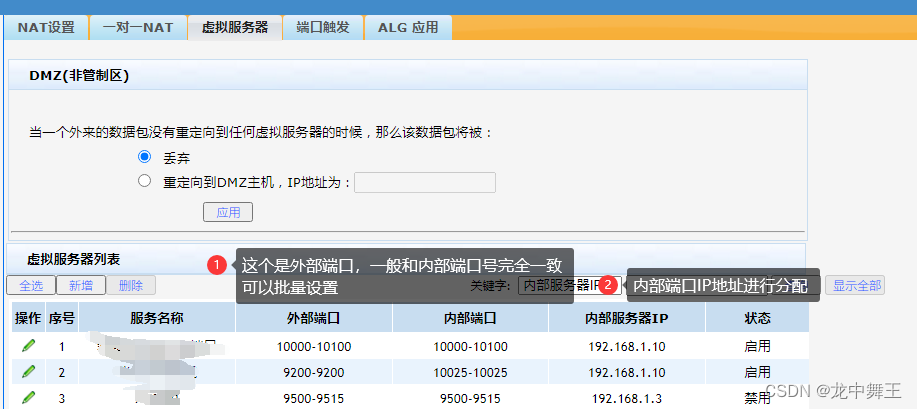
公司企业端口映射
文章目录 前言如何进行内网映射打开路由器管理网址设置端口映射 前言 公司为了提供稳定的网络服务,需要拥有一个稳定的IPV4的网络地址,一般公司有点规模的,会去电信局里面拉一根专门的网线,获取稳定的全球IPV4地址。 一个IPV4地…...

gitlab安装和使用
gitlab安装和使用 1.下载必要的依赖 sudo yum install curl openssh-server openssh-clients postfix cronie #需要执行sudo service postfix start #配置邮箱的sudo chkconfig postfix on #配置邮箱的#这句是用来做防火墙的,避免用户通过ssh方式和http来访问。su…...
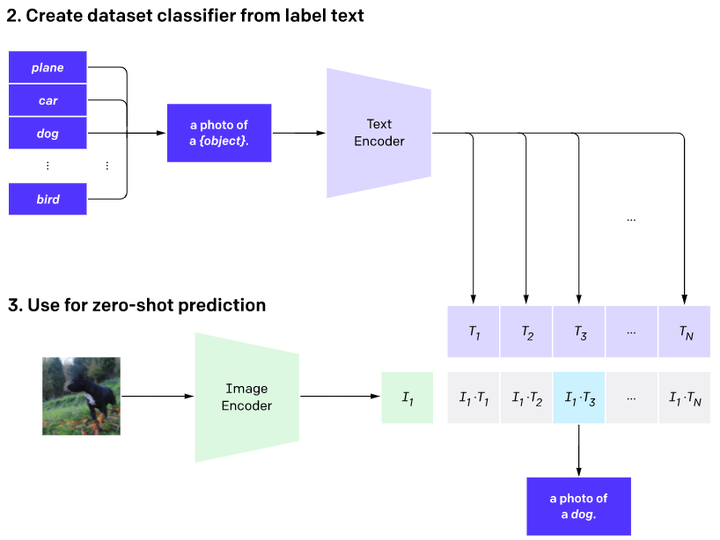
【论文阅读】DALL·E: Zero-Shot Text-to-Image Generation
OpenAI第一代文本生成图片模型 paper:https://arxiv.org/abs/2102.12092 DALLE有120亿参数,基于自回归transformer,在2.5亿 图片-文本对上训练的。实现了高质量可控的text to image,同时也有zero-shot的能力。 DALL-E没有使用扩…...

说一下 toRef、toRefs,以及他们的区别
toRef:创建一个新的Ref变量,转换Reactive对象的某个字段为Ref变量 toRefs:创建一个新的对象,它的每个字段都是Reactive对象各个字段的Ref变量 说一下toRef 先定义一个reactive对象 interface Member {id: numbername: string } c…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
