冒泡排序算法原理和代码实现,就是这么简单!
冒泡排序,是比较简单的一种排序算法。
它的命名源于它的算法原理:重复的从前往后(或者从后往前),依次比较记录中相邻的两个元素,如果他们顺序错误就把它们交换过来,直到没有再需要交换的元素,就说明该记录已完成排序。
它看起来就像是把最大的元素(或最小的元素)经由交换慢慢的‘浮’到数列的顶端,故名冒泡排序。
我们通过将一个无序数列按升序排序来演示算法原理。

如果你想学习自动化测试,我这边给你推荐一套视频,这个视频可以说是B站播放全网第一的自动化测试教程,同时在线人数到达1000人,并且还有笔记可以领取及各路大神技术交流:798478386
【已更新】B站讲的最详细的Python接口自动化测试实战教程全集(实战最新版)_哔哩哔哩_bilibili【已更新】B站讲的最详细的Python接口自动化测试实战教程全集(实战最新版)共计200条视频,包括:1、接口自动化之为什么要做接口自动化、2、接口自动化之request全局观、3、接口自动化之接口实战等,UP主更多精彩视频,请关注UP账号。![]() https://www.bilibili.com/video/BV17p4y1B77x/?spm_id_from=333.337&vd_source=488d25e59e6c5b111f7a1a1a16ecbe9a
https://www.bilibili.com/video/BV17p4y1B77x/?spm_id_from=333.337&vd_source=488d25e59e6c5b111f7a1a1a16ecbe9a
算法流程:
1. 比较相邻元素,如果第一个比第二个大,就交换它们两个。
2. 对每一组相邻元素做同样的工作,从开始到最后一对,这时最后的元素应该会是最大的数。
3. 针对所有元素重复步骤 1,2,除了最后一个元素,这时倒数第二个元素应该会是第二大的数。
4. 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
图解步骤:
有一个数列 [4, 2, 6, 5, 3, 9],通过冒泡排序的步骤如下:
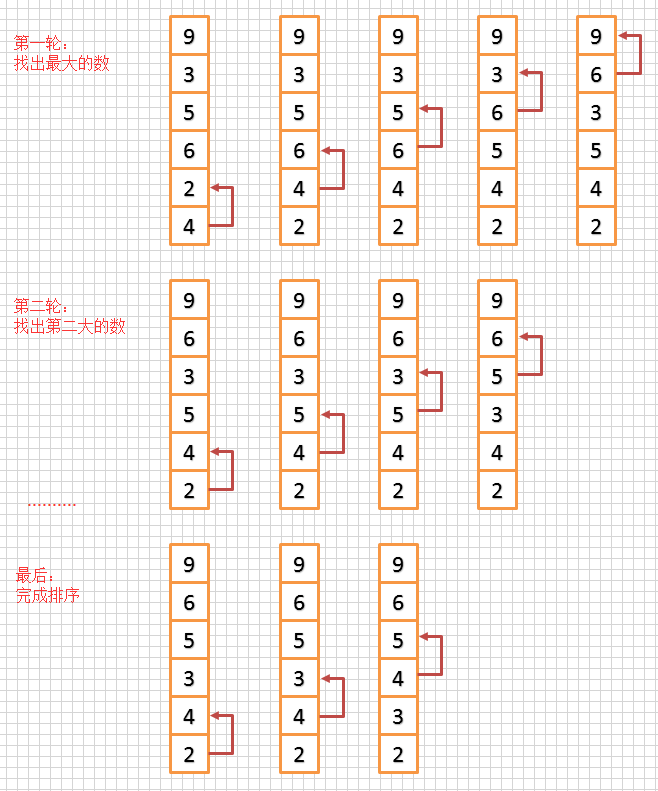
代码实现
总结:
1、一个长度为 n 的数列,我们最多需要进行 n-1 轮比较
2、第 m 轮,需要 n-m-1 次比较
根据上述思想,使用 python 代码来实现:
l = [1, 7, 5, 6, 2, 8, 3, 9, 4]
n = len(l)
for m in range(n-1): # 外层循环决定需要排序的轮次for i in range(n-m-1): # 内层循环决定要比较的次数if l[i] > l[i+1]:l[i], l[i+1] = l[i+1], l[i]print(l)输出结果:
[1, 5, 6, 2, 7, 3, 8, 4, 9]
[1, 5, 2, 6, 3, 7, 4, 8, 9]
[1, 2, 5, 3, 6, 4, 7, 8, 9]
[1, 2, 3, 5, 4, 6, 7, 8, 9]
[1, 2, 3, 4, 5, 6, 7, 8, 9] # 到这里其实已经排序结束了
[1, 2, 3, 4, 5, 6, 7, 8, 9]
[1, 2, 3, 4, 5, 6, 7, 8, 9]
[1, 2, 3, 4, 5, 6, 7, 8, 9]可以看到:循环进行了 5 次就得到了正确的结果,但是程序还是进行了剩下的循环。对上面的程序进行优化,得到下面的改进版。
l = [1, 7, 5, 6, 2, 8, 3, 9, 4]
n = len(l)
for m in range(n-1):flag = True # 设置一个标志位for i in range(n-m-1):if l[i] > l[i+1]:l[i], l[i+1] = l[i+1], l[i]flag = False # 如果本能循环还需要交换就改变flag的值if flag: # 如果flag没有改变就说明排序成功了breakprint(l)运行结果:
[1, 5, 6, 2, 7, 3, 8, 4, 9]
[1, 5, 2, 6, 3, 7, 4, 8, 9]
[1, 2, 5, 3, 6, 4, 7, 8, 9]
[1, 2, 3, 5, 4, 6, 7, 8, 9]
[1, 2, 3, 4, 5, 6, 7, 8, 9]分析总结
1. 时间复杂度
-
若列表的初始状态是正序的,一趟扫描即可完成排序。所需的比较次数 C 和移动次数 M 均为最小值:
C=n-1,M=0,所以冒泡排序的最好时间复杂度为 O(n) -
若列表的初始状态是反序的,需要进行 n-1 趟排序。每趟排序要进行 n-i 次比较,且每次比较都必须移动记录 2 次来达到交换记录的位置。在这种情况下比较和移动次数均达到最大值
C = n(n-1)/2=O(n2),M=2n(n-1)/2=O(n2)
冒泡排序的最坏时间复杂度为 O(n2)
综上,冒泡排序的平均时间复杂度为 O(n2)
2. 空间复杂度
冒泡排序算法过程中内存空间稳定,所以空间复杂度为 O(1)
3. 稳定性分析
冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。
所以,如果两个元素相等,是不会再交换的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
4. 应用分析
因为冒泡排序的时间复杂度为 O(n2),一般应用于小规模数据的排序。且冒泡排序逻辑比较简单,易于理解,一般会用于教学。
相关文章:

冒泡排序算法原理和代码实现,就是这么简单!
冒泡排序,是比较简单的一种排序算法。 它的命名源于它的算法原理:重复的从前往后(或者从后往前),依次比较记录中相邻的两个元素,如果他们顺序错误就把它们交换过来,直到没有再需要交换的元素&am…...

[工业自动化-6]:西门子S7-15xxx编程 - PLC系统硬件组成与架构
目录 一、PLC系统组成 1.1 PLC 单机系统组成 1.2 PLC 分布式系统 二、PLC各个组件 2.1 PLC上位机 2.2 PLC主站:PLC CPU控制中心 (1)主要功能 (2)主站组成 2.3 PLC分布式从站: IO模块的拉远 (1&am…...

pinpoint监控tomcat应用,页面显示No data collected
pinpoint安装部署教程大家都可以搜到。这里就不说了。单说一下 页面没有数据的情况。 部署环境,pinpoint安装部署在A服务器上。现在是在C、D、E、F……linux机器上安装pinpoint-agnet 1. 将文件 pinpoint-agent-1.8.5.tar.gz 上传到 服务器C、D、E、F…… 2. 解压…...

【左程云算法全讲4】前缀树、非比较排序
系列综述: 💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于左程云算法课程进行的,每个知识点的修正和深入主要参考…...

微头条项目实战:新增RequestHeader注解
1、RequestHeader package com.csdn.mymvc.annotation; import java.lang.annotation.*; Target(ElementType.PARAMETER) Retention(RetentionPolicy.RUNTIME) Inherited public interface RequestHeader { }2、DispatcherServlet package com.csdn.mymvc.core; import com.csd…...
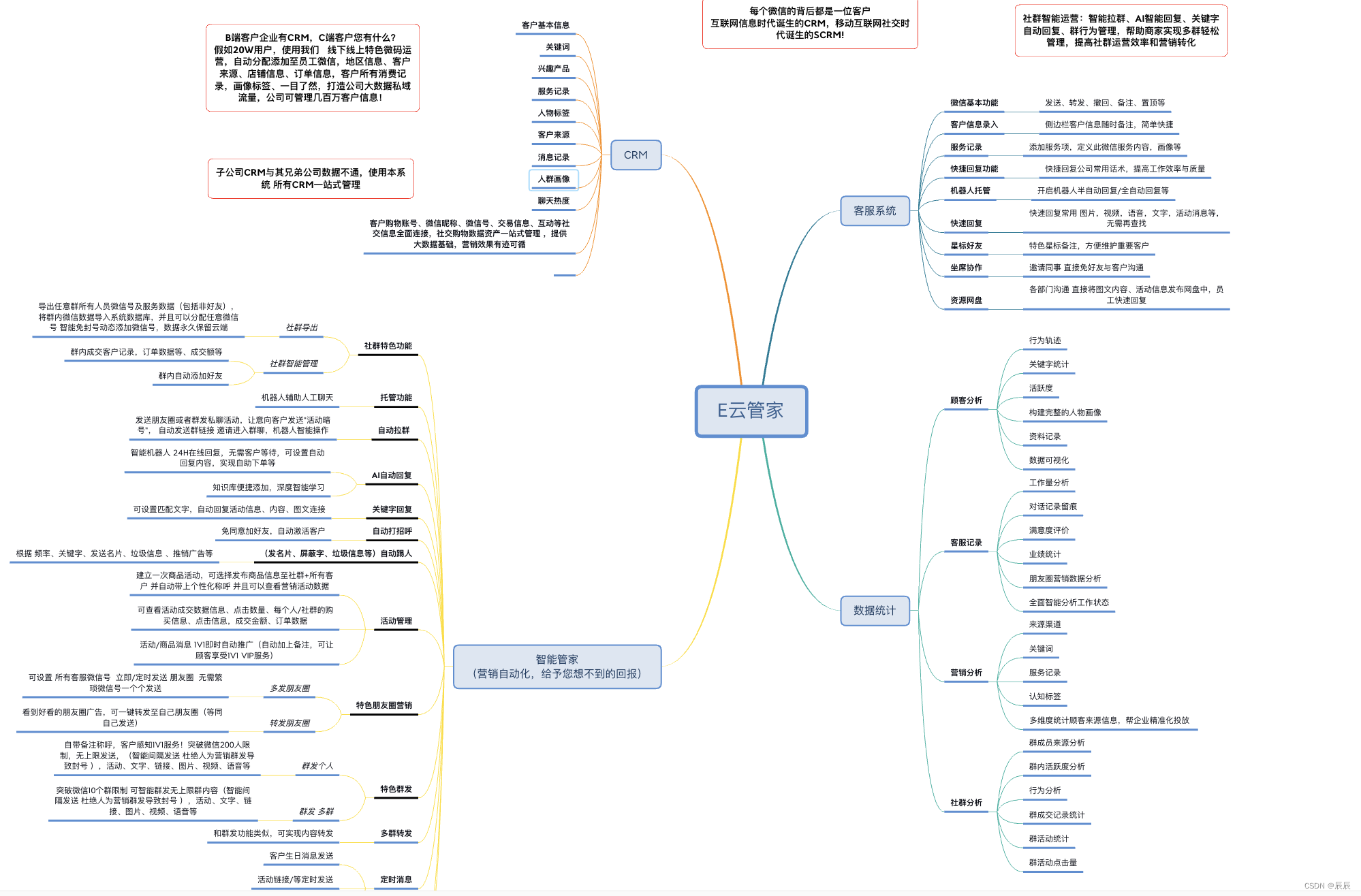
E云管家个微协议框架--新版本的利器
在互联网时代,高效、可靠的互联网协议对于实现稳定、安全的数据传输至关重要。E云管家作为一项创新性的IPAD协议构建工具,基于IPAD8.0.37协议为开发者提供了强大而灵活的功能,使他们能够轻松构建高效的通信协议。本文将介绍E云管家的主要特点…...

百度上线“文心一言”付费版本,AI聊天机器人市场竞争加剧
原创 | 文 BFT机器人 百度不愧是我国AI技术领域的先行者,每年致力于人工智能领域取得技术产品的突破和创新。据爆料称,百度的文心一言有突破了新境界,开创了文心大模型4.0会员版本。从线上的to C产品到试水商业化,百度都是争先走…...
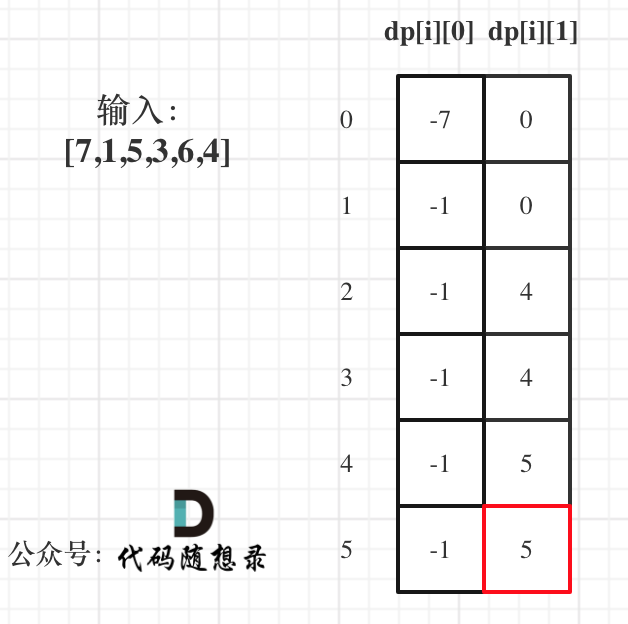
代码随想录算法训练营第四十七天丨 动态规划part10
121. 买卖股票的最佳时机 思路 动态规划 动规五部曲分析如下: 确定dp数组(dp table)以及下标的含义 dp[i][0] 表示第i天持有股票所得最多现金 ,这里可能有疑惑,本题中只能买卖一次,持有股票之后哪还有…...

微前端:quankun
零: 前言 微前端可以将大应用拆分功能独立的微应用,可独立开发部署, 每个微应用可以采用自己的技术栈,这样更好维护和拓展。微前端也会存在跨域 权限控制 数据共享 性能(页面加载时间) 安全 多团队协作(一个团队负责一个页面或模…...
CSDN每日一题学习训练——Java版(克隆图、最接近的三数之和、求公式的值)
版本说明 当前版本号[20231109]。 版本修改说明20231109初版 目录 文章目录 版本说明目录克隆图题目解题思路代码思路参考代码 最接近的三数之和题目解题思路代码思路参考代码 求公式的值题目解题思路代码思路参考代码 克隆图 题目 给你无向 连通(https://baike.baidu.com…...

XOR Construction
思路: 通过题目可以得出结论 b1^b2a1 b2^b3a2 ....... bn-1^bnan-1 所以就可以得出 (b1^b2)^(b2^b3)a1^a2 b1^b3a1^a2 有因为当确定一个数的时候就可以通过异或得到其他所有的数,且题目所求的是一个n-1的全排列 那么求出a的前缀异或和arr之后…...
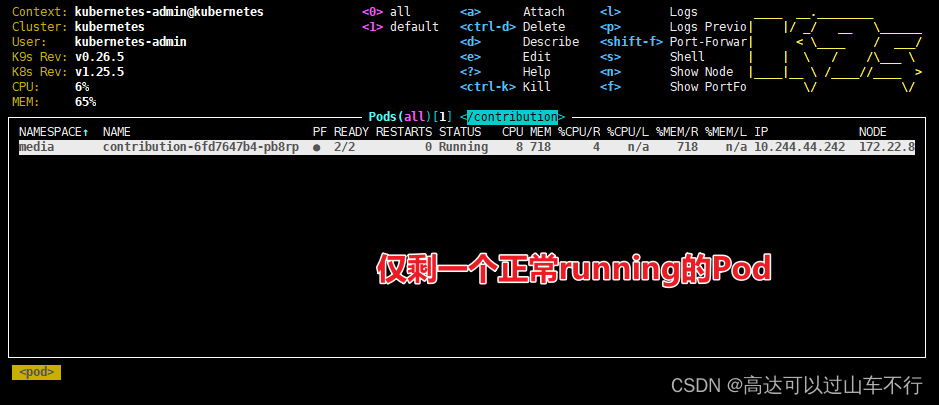
K8S容器持续Terminating无法正常关闭(sider-car容器异常,微服务容器正常)
问题 K8S上出现大量持续terminating的Pod,无法通过常规命令删除。需要编写脚本批量强制删除持续temminating的Pod:contribution-xxxxxxx。 解决 获取terminating状态的pod名称的命令: # 获取media命名空间下,名称带contributi…...

Spring 循环依赖
文章目录 内容总结循环依赖 内容总结 循环依赖 循环依赖只存在于 Spring 中, 是因为 Spring 创建 Bean 的流程中, 依赖注入阶段, 会先从单例池中找, 没有再从定义池中找, 针对定义池中找到的候选项会通过 getBean 创建其单例并缓存到单例池, 此机制导致了存在循环依赖的问题.…...

MySQL 8.0.13升级到8.0.35记录 .NET
1、修改表结构的字符集 utf8 修改成 utf8mb4 utf8_general_ci 修改成 utf8mb4_0900_ai_ci 注:所有地方都要替换。 否则会报错误提示:Character set utf8mb3 is not supported 下面是.NET环境升级遇到的问题 2、MySQL Connector Net 8.0.13 在程…...

flink udtaf 常年不能用
[FLINK-32807] when i use emitUpdateWithRetract of udtagg,bug error - ASF JIRA flink1.18发布的时候 他都显示未解决 但是文档上一直有udtaf...

路由汇总的四要点
1.是基于链路级的还是进程级的? RIP和eigrp都是基于接口的链路级汇总,而OSPF是基于进程的 2.汇总路由什么时候消失? 最后一条明细路由消失的时候,汇总路由消失。 3.汇总之后,汇总路由被通告,本地是否会产生一条指向NULL接口的…...
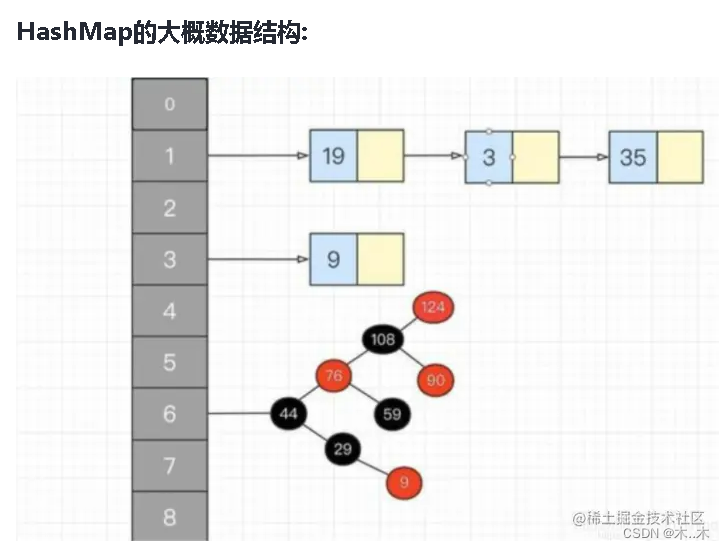
HashMap存值、取值及哈希碰撞原理分析
HashMap中的put()和get()的实现原理: map.put(k,v)实现原理 首先将k,v封装到Node对象当中(节点)。 然后它的底层会调用K的hashCode()方法得出hash值。 通过哈希表函数/哈希算法,将hash值转换成数组的下标,下标位置上…...

【SVN】
SVN 1 svn使用1.1 主干合并到分支1.2 分支合并到主干1.3 分支建立1.4 创建分支1.5 切换分支1.6 合并分支1.7 删除分支 2 概念理解 1 svn使用 1.1 主干合并到分支 首先,在本地trunk中先update一下,有冲突的解决冲突,保证trunk和repository已…...

编程语言,脚本语言
脚本语言上手快,快速实现一个小应用如python;编程语言重型,需复杂的设计和较长时间的开发,如java、c...
探索双十一:从技术角度剖析电商狂欢节
每年的11月11日,全球最大的在线购物狂欢节“双十一”在中国掀起了一场规模空前的消费风暴。以阿里巴巴为代表的电商平台和众多品牌商家,不仅为消费者提供了数以亿计的优惠商品,同时也将这一活动打造成了一个科技与商业完美结合的标志事件。本…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...
