简述SVM
概述
SVM,即支持向量机(Support Vector Machine),是一种常见的监督学习算法,用于分类和回归问题。它是一种基于统计学习理论和结构风险最小化原则的机器学习方法。
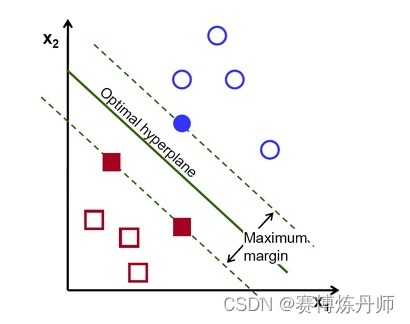
SVM的主要思想是在特征空间中找到一个最优的超平面,将不同类别的样本点分隔开来。这个超平面可以被视为一个决策边界,用于对新的样本进行分类。SVM的目标是找到具有最大间隔(下图中margin的一半)的超平面,以实现更好的泛化性能。
超平面公式怎么推导
假设x0为超平面上的一点,w为超平面的法向量,对于超平面上任意的一点x都存在
w·(x-x0) = w·x - w·x0 = 0
令-w·x0 = b,则变为
w·x + b = 0
函数距离和几何距离
在超平面w·x + b = 0确定的情况下,|w·x + b|可以相对地表示点x距离超平面的远近,对于二分类问题,如果w·x + b > 0,则x的类别被判定为1,否则判定为-1。如果y(w·x + b) > 0,则x的分类正确,并且y(w·x + b)的值越大,分类结果的确信度越大。
所以样本点(xi,yi)与超平面(w,b)之间的函数距离定义为d = yi(w·xi + b)
但是该定义存在问题,即w和b同时缩放k倍后,超平面没有变化(比如w·x + b = 0和2w·x + 2b = 0是同一个超平面),但是函数距离却变化了,于是我们需要求几何距离。
几何距离可以通过面与面的距离公式来算,因为离超平面最近的样本点其实可以看作是处在一个和超平面平行的面上,所以我们要求的其实是面w·x + b = 1和面w·x + b = 0的距离,由距离公式可得d = 1/||w||。
于是我们得到
拉格朗日乘子法
再进行下一步之前,我们先来了解一下拉格朗日乘子法。
拉格朗日乘子法是一种在最优化的问题中寻找多元函数在其变量受到一个或多个条件的约束时的求局部极值的方法。这种方法可以将一个有n个变量和k个约束条件的最优化问题转换为一个解有n + k个变量的方程组的解的问题。
举个例子:求双曲线xy = 3上离原点最近的点。
首先根据问题得出min f(x,y) = x^2 + y^2 s.t. xy = 3
如下图
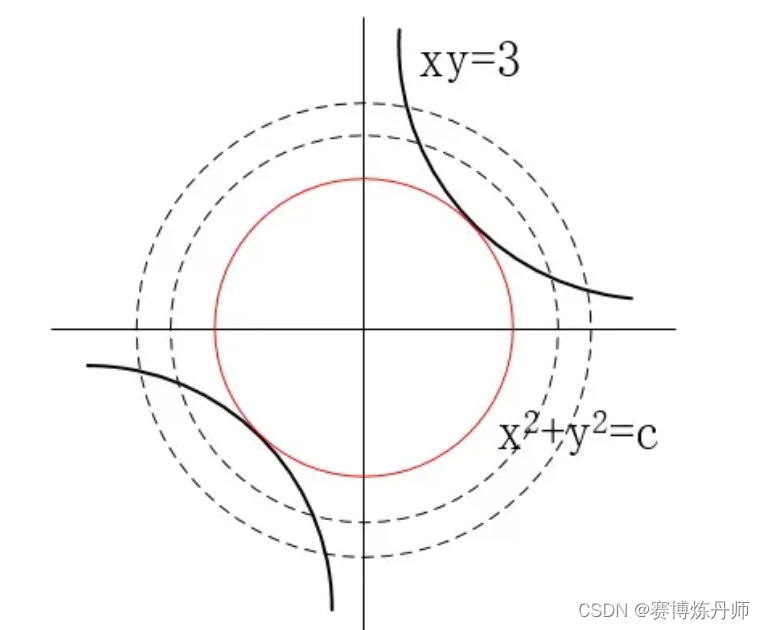
可以看出,xy = 3和f(x,y) = x^2 + y^2的曲线簇的切点,就是我们要求的距离原点最近的点。
又有如果两个曲线相切,那么它们的切线相同,即法向量是相互平行的,于是由▽f//▽g可得▽f = λ*▽g。
这时,就将原有的约束优化问题转化为了一种对偶的无约束优化问题
| 原问题: | 对偶问题: |
| min f(x,y) = x2 + y2 s.t. xy = 3 | 由▽f = λ*▽g得: fx = λ*gx (1) xy = 3 |
| 约束优化问题 | 无约束方程组问题 |
接着对上面的(1)式分别对x和y求偏导,得到2x = λ*y, 2y = λ*x, xy = 3
通过求解方程得λ = ±2,当λ = 2时,x = sqrt(3),y = sqrt(3)或者x = sqrt(3),y = sqrt(3);当λ = -2时无解。
从等式约束到非等式约束
现在回到之前的问题,我们发现,在上面的例子中,约束条件是一个等式,而在我们的问题中约束条件s.t. yi(w·xi + b) - 1 >= 0,i=1,2,...,n是一个不等式,那么非等式约束又该怎么处理呢?
下图展示了拉格朗日乘子法的几何含义:红色曲线表示等式约束g(x) = 0,红色曲线围成的曲面内表示非等式约束g(x) <= 0
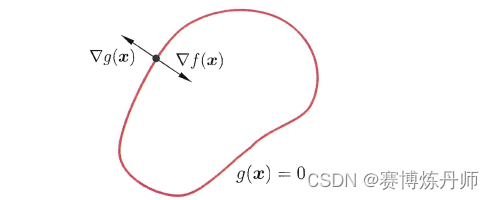
非等式约束g(x) <= 0的情形中,最优点x要么出现在边界g(x) = 0上,要么出现在区域g(x) < 0中,
对于g(x) < 0的情况,因为▽f(x)方向向里,因此约束条件g(x) <= 0不起作用,我们只需要通过条件▽f(x) = 0求得可能的极值即可
对于g(x) = 0的情况,类似于之前提到的等式约束,但是▽f(x)的方向和▽g(x)的方向必须相反,即存在常数λ > 0使得▽f(x) + λ*▽g(x) = 0
当最优值落在g(x) < 0区域时,约束条件g(x) <= 0不起作用,因此我们令约束条件的乘子λ = 0,当最优值落在g(x) = 0边界上时,λg(x)自然等于0。综合这两种情况,可以推出λg(x) = 0。
因此,拉格朗日乘子法可以写成如下的等价形式,括号中的条件也叫做KKT条件。
L(x,λ) = f(x) + λ*g(x)
从原函数到对偶问题
接着考虑之前得到的目标函数
由于求的最大值相当于求
的最小值,所以上述目标函数等价于
因为现在的目标函数是二次的,约束条件是线性的,所以它是一个凸二次规划问题(之所以等价于而不是等价于
就是为了将它转化为一个凸二次规划问题)
此外,由于这个问题的特殊结构,还可以通过拉格朗日对偶性变换到对偶变量的优化问题,即通过求解与原问题等价的对偶问题得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。
那什么是拉格朗日对偶性呢?简单来讲,通过给每一个约束条件加上一个拉格朗日乘子α,定义拉格朗日函数如下
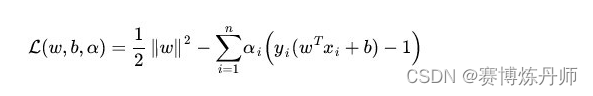
然后令

容易验证,当某个约束条件不满足时,例如,那么显然有
(只要令
即可)。而当所有约束条件都满足时,则最优值为
,亦即最初要最小化的量。
因此,在要求约束条件得到满足的情况下最小化,实际上等价于直接最小化
(当然,这里也有约束条件,就是
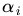
会等于无穷大,自然不会是我们所要求的最小值。
具体写出来,目标函数变成了:
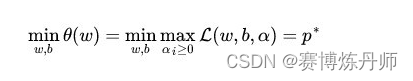
这里用表示这个问题的最优值,且和最初的问题是等价的。如果直接求解,那么一上来便得面对w和b两个参数,而
又是不等式约束,这个求解过程不好做。不妨把最小和最大的位置交换一下,变成:
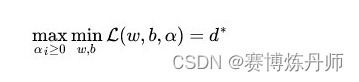
交换以后的新问题是原始问题的对偶问题,这个新问题的最优值用来表示。而且有
≤
,在满足某些条件的情况下(这个条件指的是强对偶,Slater条件是强对偶的充分条件),这两者相等,即
=
,这个时候就可以通过求解对偶问题来间接地求解原始问题。
换言之,之所以从minmax的原始问题,转化为maxmin的对偶问题
,一者因为
是
的近似解,二者,转化为对偶问题后,更容易求解。
所谓Slater 条件,即指:凸优化问题,如果存在一个点x,使得所有等式约束都成立,并且所有不等式约束都严格成立(即取严格不等号,而非等号),则满足Slater 条件。对于此处,Slater条件成立,所以≤
可以取等号,即
=
,所以我们对对偶问题的求解等价于对原问题的求解。
下面可以先求L 对w、b的极小,再求L 对的极大。
对偶问题的求解
先让拉格朗日函数分别对w和b求偏导

将以上结果代入
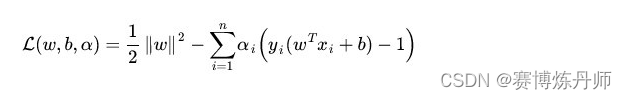
得
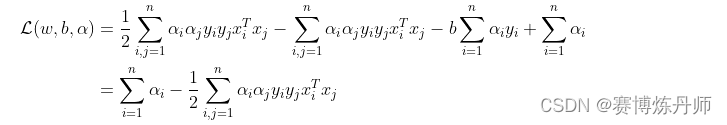
求对的极大,即是关于对偶问题的最优化问题。经过上面第一个步骤的求w和b,得到的拉格朗日函数式子已经没有了变量w,b,只有
。从上面的式子得到:
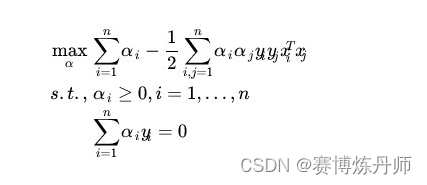
这样,求出了,根据
,即可求出w,然后通过
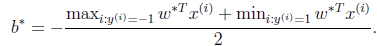 ,即可求出b,最终得出分离超平面和分类决策函数。
,即可求出b,最终得出分离超平面和分类决策函数。
在求得L(w, b, a) 关于 w 和 b 最小化,以及对的极大之后,最后一步则可以利用SMO算法求解对偶问题中的拉格朗日乘子
。
相关文章:
简述SVM
概述 SVM,即支持向量机(Support Vector Machine),是一种常见的监督学习算法,用于分类和回归问题。它是一种基于统计学习理论和结构风险最小化原则的机器学习方法。 SVM的主要思想是在特征空间中找到一个最优的超平面…...

【DevOps】Rundeck以及Jenkins
Rundeck是一个DevOps常用的工具,是PagerDuty公司开发的产品,能够很好的和PagerDuty进行集成。 但是平常我们听得或用得更多的是Jenkins,一个非常流行的CI工具,具有很好的可扩展性。 可是为什么那家公司会用Rundeck而不是Jenkins呢…...

数字滤波器分析---零极点分析
数字滤波器分析---零极点分析 zplane 函数绘制线性系统的极点和零点。 例如,在 -1/2 处为零且在 0.9e−j2π0.3 和 0.9ej2π0.3 处有一对复极点的简单滤波器为 zer -0.5; pol 0.9*exp(j*2*pi*[-0.3 0.3]); 要查看该滤波器的零极点图,您可以使用 z…...

HarmonyOS应用开发-网络请求与web组件
前言 当今世界,移动应用已经成为人们日常生活中不可或缺的一部分。无论是社交媒体、新闻、购物还是娱乐,安卓应用的广泛使用已经改变了我们与数字世界互动的方式。然而,这些应用的实际功能远不止界面和用户体验。它们背后的精密技术和网络请…...

频次最高的38道selenium面试题及答案
1、selenium的原理是什么? selenium的原理涉及到3个部分,分别是: 浏览器driver:一般我们都会下载driverclient:也就是我们写的代码 client其实并不知道浏览器是怎么工作的,但是driver知道,在…...
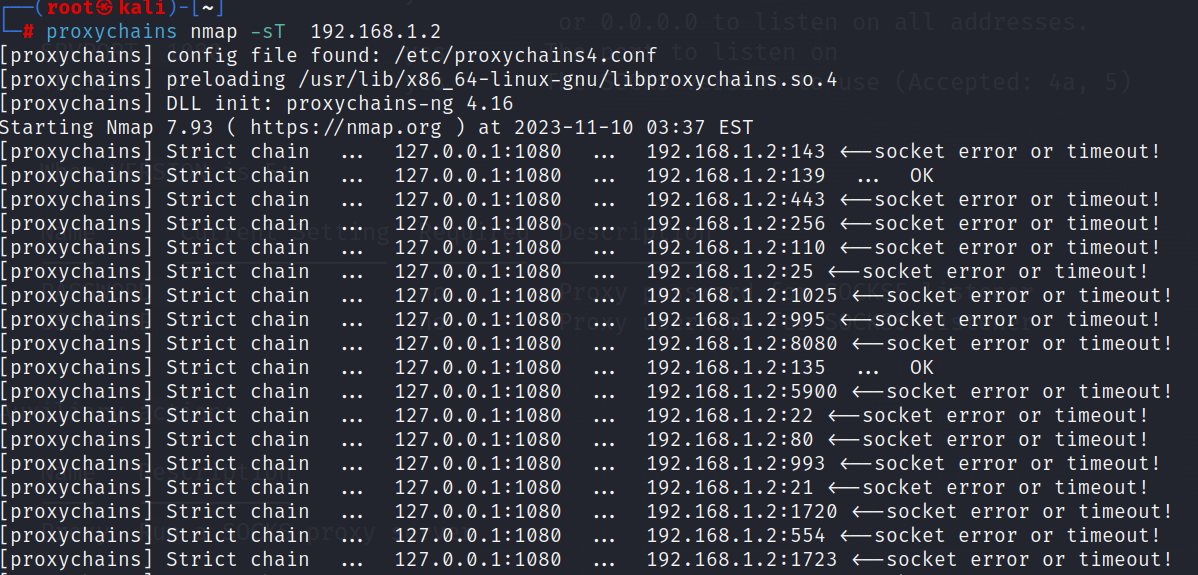
利用MSF设置代理
1、介绍: 通过MSF拿到一个机器的权限后,通过MSF搭建socks代理,然后通内网。 拿到目标权限,有很多方法,比如:①ms17-010 ②补丁漏洞 ③MSF生成后门 在此直接使用MSF生成后门 MSF中有三个代理模块&#x…...
模型剪枝算法——L1正则化BN层的γ因子
ICCV在2017年刊登了一篇经典论文《 Learning Efficient Convolutional Networks through Network Slimming》。在神经网络的卷积操作之后会得到多个特征图,通过策略突出重要的特征达到对网络瘦身的目的。在该论文中使用的剪枝策略就是稀疏化BN层中的缩放因子 。 Bat…...
)
11.9 知识总结(三板斧、全局配置文件、静态文件的配置、request对象等)
一、 三板斧的使用 三个方法: HttpResponse render redirect def index(request): print(request) # return HttpResponse("request") # 它返回的是字符串 # return render(request, index.html) # 加载HTML页面的 # return redirect(ht…...
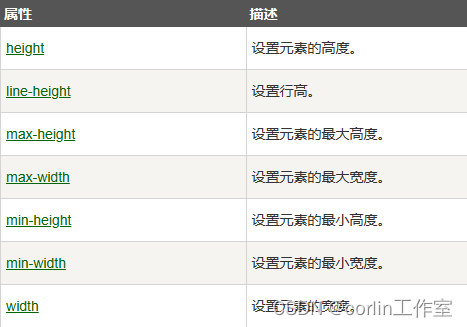
CSS 外边距、填充、分组嵌套、尺寸
一、CSS 外边距: CSS margin(外边距)属性定义元素周期的空间。margin清除周围的(外边框)元素区域。margin没有背景颜色,是完全透明的。margin可以单独改变元素的上、下、左、右边距,也可以一次改…...

Exploration by random network distillation论文笔记
Exploration by Random Network Distillation (2018) 随机网络蒸馏探索 0、问题 这篇文章提出的随机网络蒸馏方法与Curiosity-driven Exploration by Self-supervised Prediction中提出的好奇心机制的区别? 猜想:本文是基于随机网络蒸馏提出的intrin…...

Ubuntu22.04配置Go环境
Ubuntu上配置Go环境biCentOS简单多了,有两种方案,一种直接使用apt进行安装,一种自己从官网下载安装包进行安装。 1、使用apt直接安装 更新apt安装包,常规操作 apt update 然后看看apt自带的Go版本是多少 apt list golang 是1…...
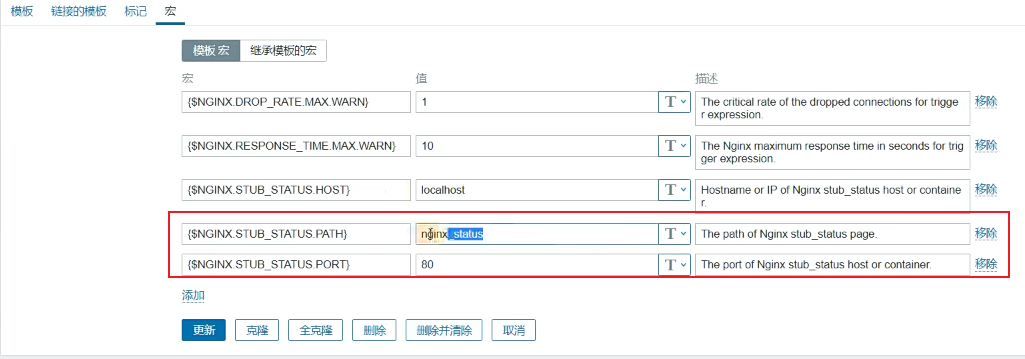
Zabbix深入解析与实战
1.Zabbix 1.1.监控概述 监控是指对行为、活动或其他变动中信息的一种持续性关注,通常是为了对人达成影响、管理、指导或保护的目的 监控 监视主机架构状态控制,事后追责目标:早发现早处理(故障、性能、架构) 网站扩容(用数据说话) 为什么要…...

怎么用电脑开发安卓app?能外包吗?
随着智能手机的普及,安卓应用程序的开发需求也越来越高,许多人都想开发自己的安卓应用程序,但苦于缺乏相关知识和技能,本文将介绍如何使用电脑开发安卓应用程序,以及是否可以将开发工作外包给专业的开发团队。 一、了…...
1-前端基本知识-HTML
1-前端基本知识-HTML 文章目录 1-前端基本知识-HTML总体概述什么是HTML?超文本标记语言 HTML基础结构文档声明根标签头部元素主体元素注释 HTML概念词汇:标签、属性、文本、元素HTML基本语法规则HTML常见标签标题标签段落标签换行标签列表标签超链接标签…...

磁盘的分区、格式化、检验与挂载 ---- fdisk,mkfs,mount
磁盘的分区、格式化、检验与挂载 磁盘管理是非常重要的,当我们想要再系统里面新增一块磁盘使用时,应执行如下几步: 对磁盘进行划分,以建立可用的硬盘分区 (fdisk / gdisk)对硬盘分区进行格式化࿰…...

Solr搜索参数详解
Solr 页面搜索 1.1 基本查询 参数意义q查询的关键字,此参数最为重要,例如,qid:1,默认为q:,fl指定返回哪些字段,用逗号或空格分隔,注意:字段区分大小写,例如,…...
Flink(三)【运行时架构】
前言 今天学习 Flink 的一些原理性的东西,比较偏概念,但是十分重要。有人觉得上来框框敲代码才能学到东西,那是狗屁不通的道理(虽然我以前也这么认为)。个人认为,学习 JavaEE那些框架,你上来就敲…...

conda添加清华镜像源
一、conda下载 https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/ 显示所有channel conda config --show channels 二、添加清华镜像源 conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ conda config --add channels https://…...
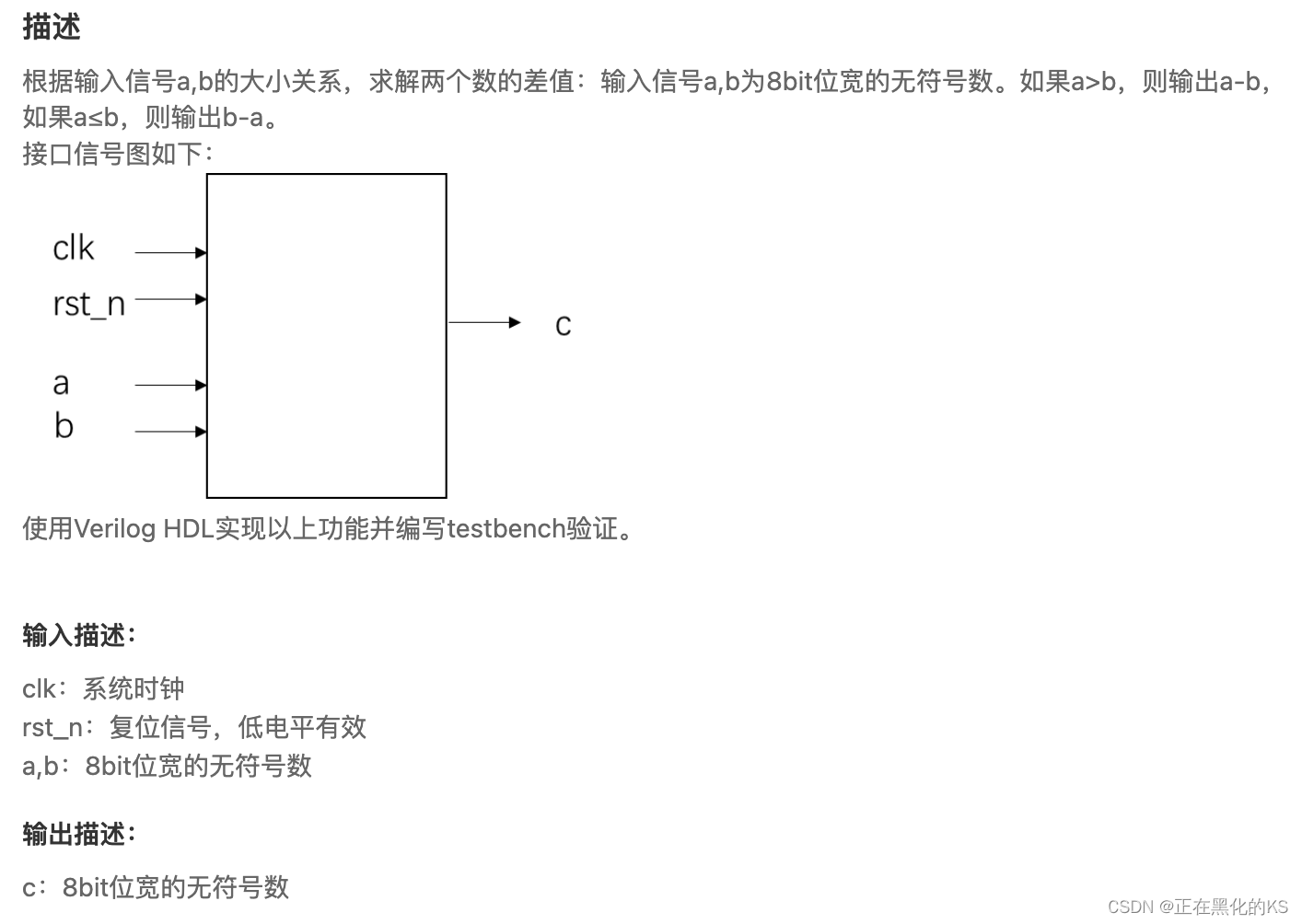
「Verilog学习笔记」求两个数的差值
专栏前言 本专栏的内容主要是记录本人学习Verilog过程中的一些知识点,刷题网站用的是牛客网 timescale 1ns/1ns module data_minus(input clk,input rst_n,input [7:0]a,input [7:0]b,output reg [8:0]c );always (posedge clk or negedge rst_n) begin if (~rst_…...
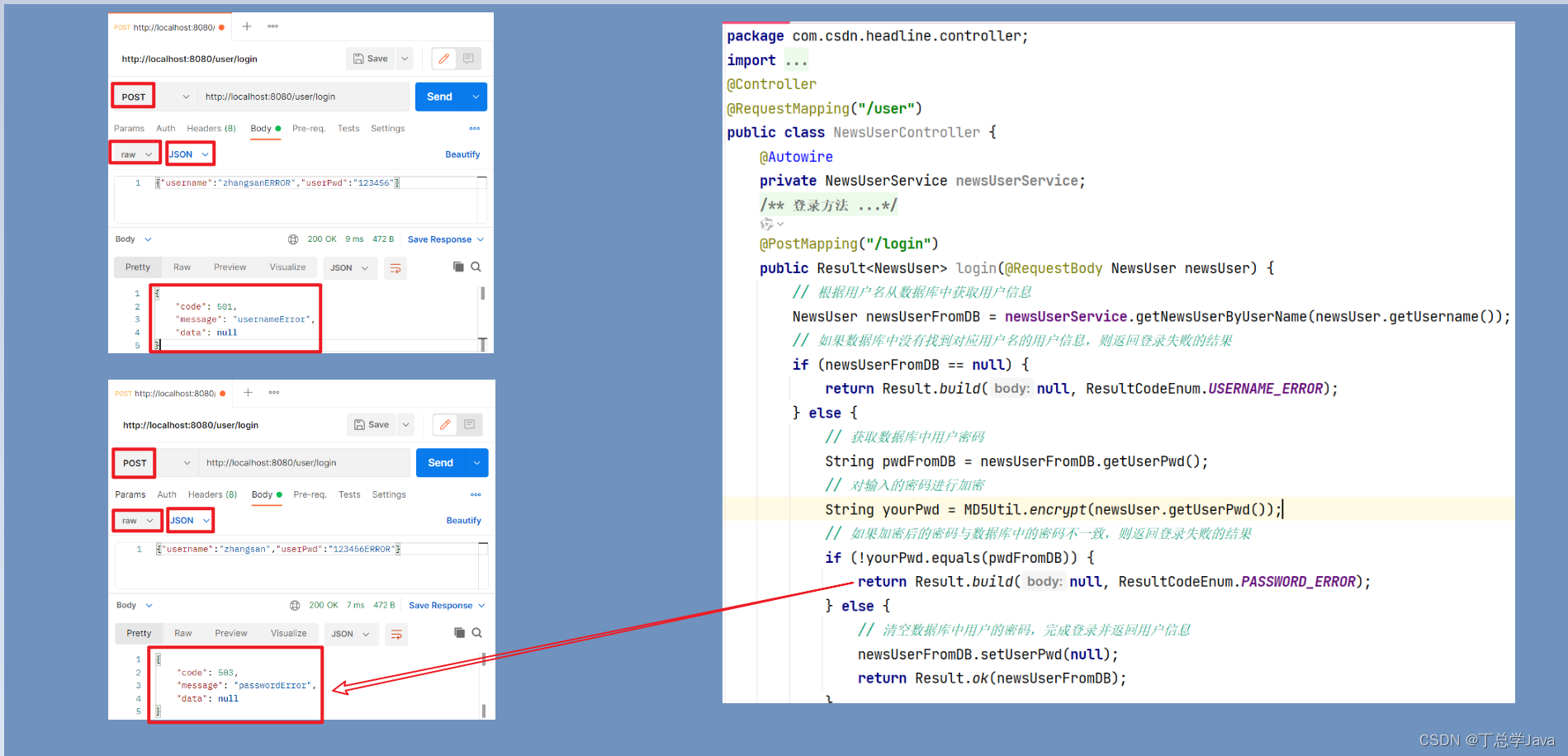
微头条项目实战:通过postman测试登录验证请求
1、CrosFilter package com.csdn.headline.filters; import jakarta.servlet.*; import jakarta.servlet.http.HttpServletResponse; import java.io.IOException; public class CrosFilter implements Filter {/*** 过滤器方法,用于处理HTTP请求* param servletReq…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
