模型剪枝算法——L1正则化BN层的γ因子



L2正则化用来平滑特征,防止过拟合。目标函数携带L2正则项表示:
L2正则化函数及求导函数的图像:

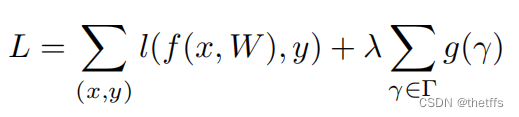
相关文章:
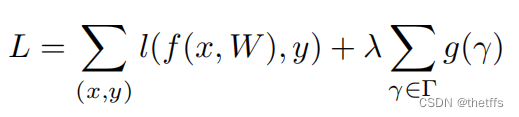
模型剪枝算法——L1正则化BN层的γ因子
ICCV在2017年刊登了一篇经典论文《 Learning Efficient Convolutional Networks through Network Slimming》。在神经网络的卷积操作之后会得到多个特征图,通过策略突出重要的特征达到对网络瘦身的目的。在该论文中使用的剪枝策略就是稀疏化BN层中的缩放因子 。 Bat…...
)
11.9 知识总结(三板斧、全局配置文件、静态文件的配置、request对象等)
一、 三板斧的使用 三个方法: HttpResponse render redirect def index(request): print(request) # return HttpResponse("request") # 它返回的是字符串 # return render(request, index.html) # 加载HTML页面的 # return redirect(ht…...
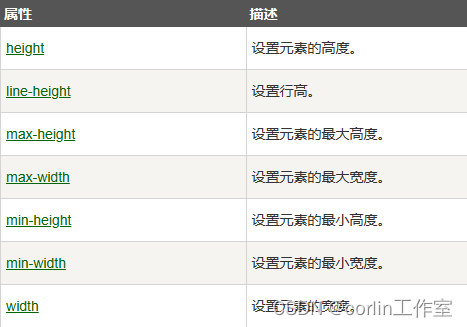
CSS 外边距、填充、分组嵌套、尺寸
一、CSS 外边距: CSS margin(外边距)属性定义元素周期的空间。margin清除周围的(外边框)元素区域。margin没有背景颜色,是完全透明的。margin可以单独改变元素的上、下、左、右边距,也可以一次改…...

Exploration by random network distillation论文笔记
Exploration by Random Network Distillation (2018) 随机网络蒸馏探索 0、问题 这篇文章提出的随机网络蒸馏方法与Curiosity-driven Exploration by Self-supervised Prediction中提出的好奇心机制的区别? 猜想:本文是基于随机网络蒸馏提出的intrin…...

Ubuntu22.04配置Go环境
Ubuntu上配置Go环境biCentOS简单多了,有两种方案,一种直接使用apt进行安装,一种自己从官网下载安装包进行安装。 1、使用apt直接安装 更新apt安装包,常规操作 apt update 然后看看apt自带的Go版本是多少 apt list golang 是1…...
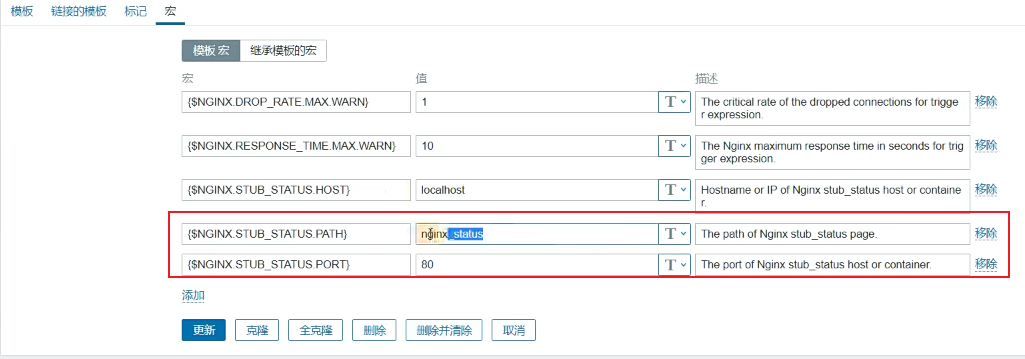
Zabbix深入解析与实战
1.Zabbix 1.1.监控概述 监控是指对行为、活动或其他变动中信息的一种持续性关注,通常是为了对人达成影响、管理、指导或保护的目的 监控 监视主机架构状态控制,事后追责目标:早发现早处理(故障、性能、架构) 网站扩容(用数据说话) 为什么要…...

怎么用电脑开发安卓app?能外包吗?
随着智能手机的普及,安卓应用程序的开发需求也越来越高,许多人都想开发自己的安卓应用程序,但苦于缺乏相关知识和技能,本文将介绍如何使用电脑开发安卓应用程序,以及是否可以将开发工作外包给专业的开发团队。 一、了…...
1-前端基本知识-HTML
1-前端基本知识-HTML 文章目录 1-前端基本知识-HTML总体概述什么是HTML?超文本标记语言 HTML基础结构文档声明根标签头部元素主体元素注释 HTML概念词汇:标签、属性、文本、元素HTML基本语法规则HTML常见标签标题标签段落标签换行标签列表标签超链接标签…...

磁盘的分区、格式化、检验与挂载 ---- fdisk,mkfs,mount
磁盘的分区、格式化、检验与挂载 磁盘管理是非常重要的,当我们想要再系统里面新增一块磁盘使用时,应执行如下几步: 对磁盘进行划分,以建立可用的硬盘分区 (fdisk / gdisk)对硬盘分区进行格式化࿰…...

Solr搜索参数详解
Solr 页面搜索 1.1 基本查询 参数意义q查询的关键字,此参数最为重要,例如,qid:1,默认为q:,fl指定返回哪些字段,用逗号或空格分隔,注意:字段区分大小写,例如,…...
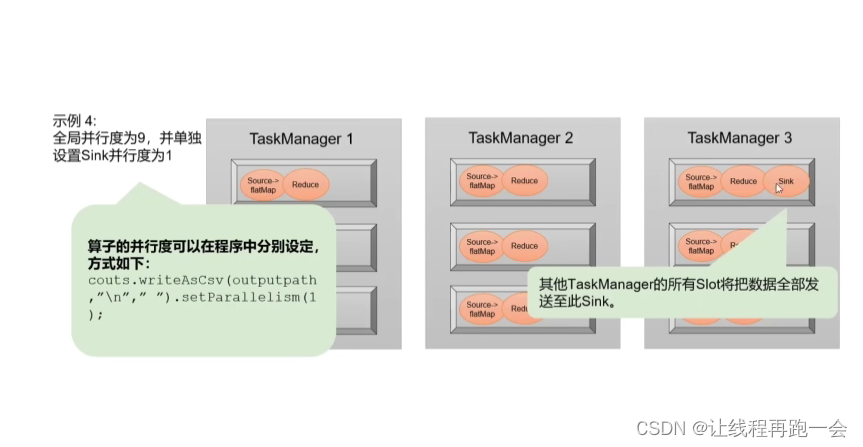
Flink(三)【运行时架构】
前言 今天学习 Flink 的一些原理性的东西,比较偏概念,但是十分重要。有人觉得上来框框敲代码才能学到东西,那是狗屁不通的道理(虽然我以前也这么认为)。个人认为,学习 JavaEE那些框架,你上来就敲…...

conda添加清华镜像源
一、conda下载 https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/ 显示所有channel conda config --show channels 二、添加清华镜像源 conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ conda config --add channels https://…...
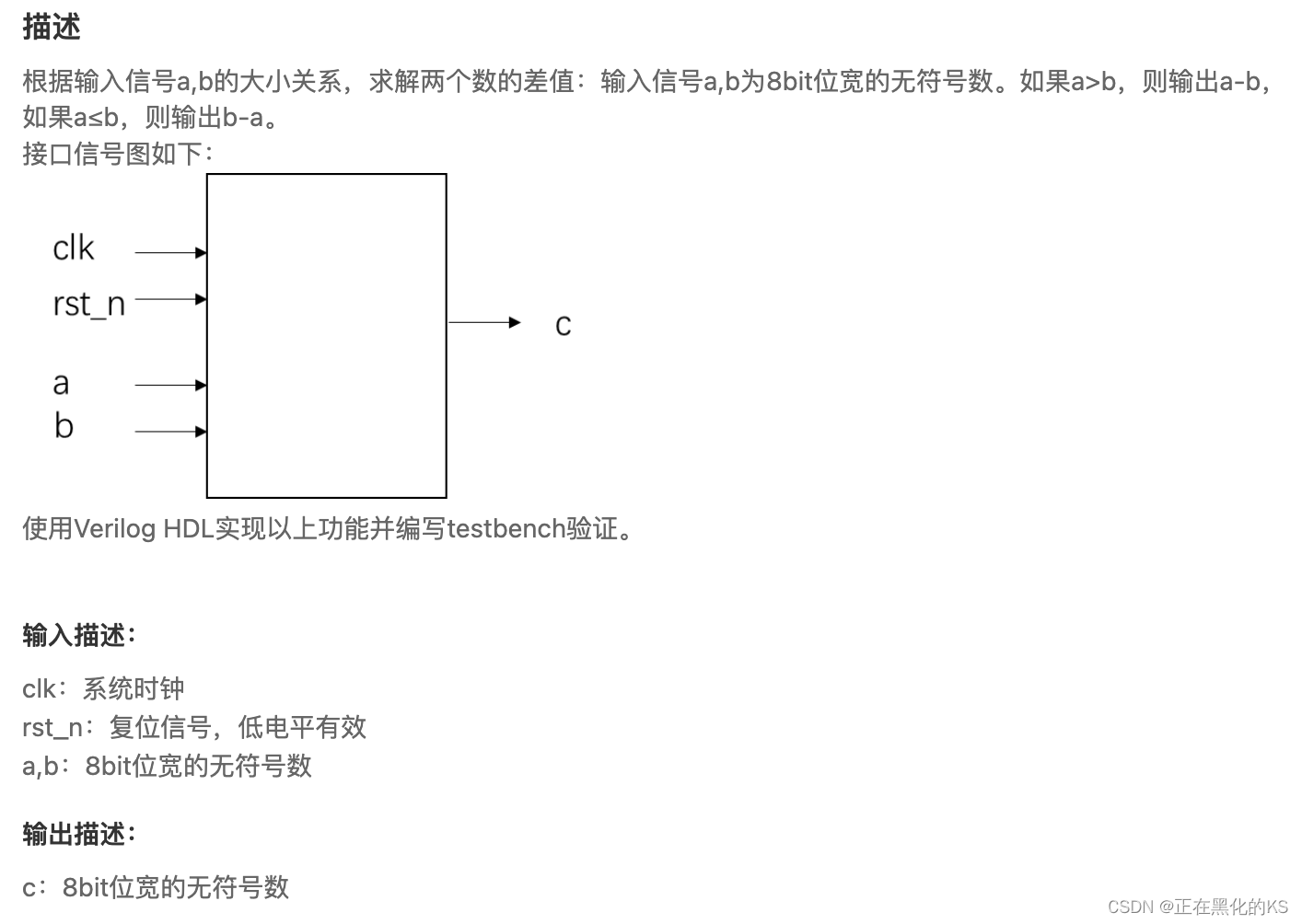
「Verilog学习笔记」求两个数的差值
专栏前言 本专栏的内容主要是记录本人学习Verilog过程中的一些知识点,刷题网站用的是牛客网 timescale 1ns/1ns module data_minus(input clk,input rst_n,input [7:0]a,input [7:0]b,output reg [8:0]c );always (posedge clk or negedge rst_n) begin if (~rst_…...
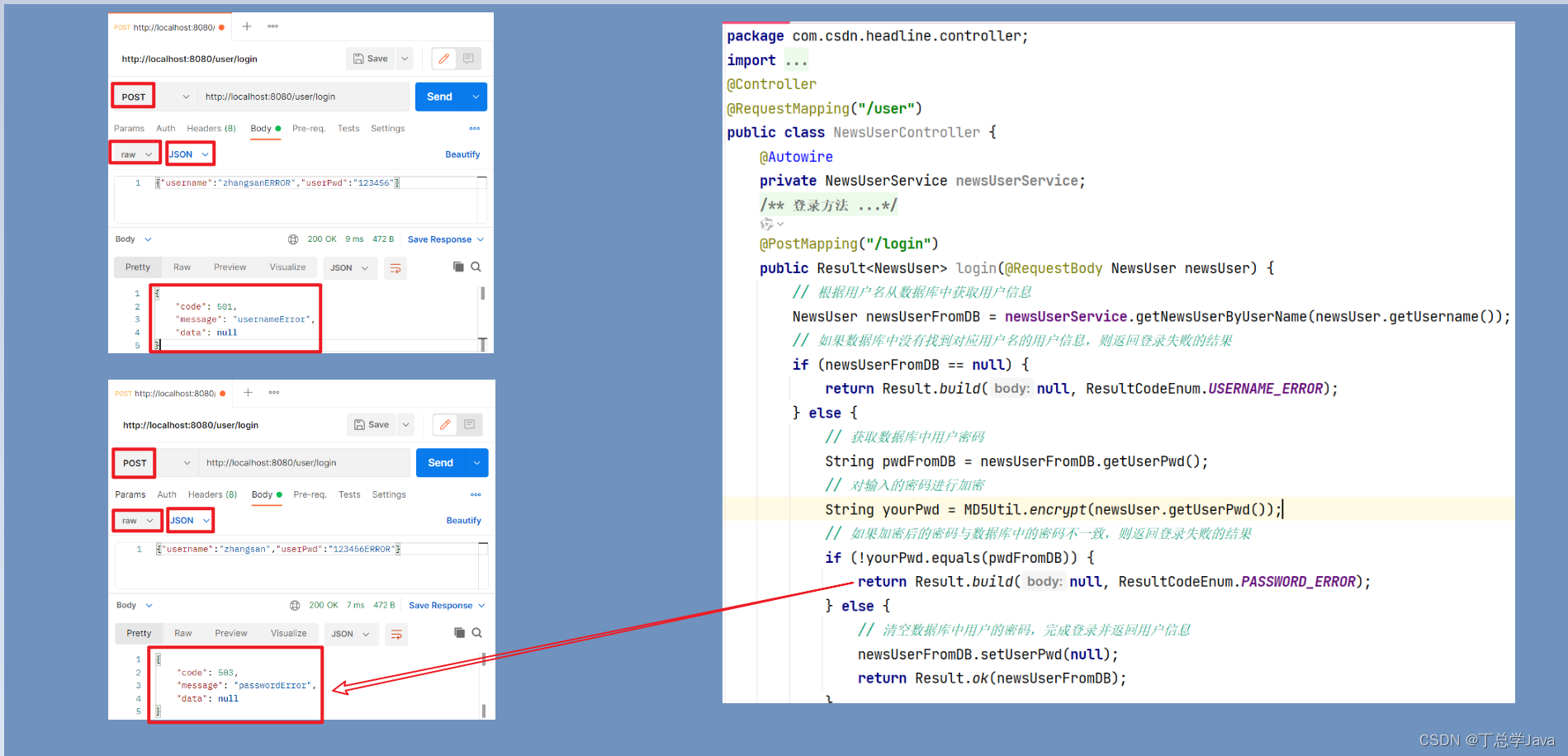
微头条项目实战:通过postman测试登录验证请求
1、CrosFilter package com.csdn.headline.filters; import jakarta.servlet.*; import jakarta.servlet.http.HttpServletResponse; import java.io.IOException; public class CrosFilter implements Filter {/*** 过滤器方法,用于处理HTTP请求* param servletReq…...

ARCGIS SERVER WMS、WFS服务添加过滤条件
我们知道geoserver中的wms,wfs过滤参数为cql_filter。比如过滤字段“mc”为"恒宇花园"的数据: cql_filtermc‘恒宇花园 但是arcgis server有所不同。具体可以看下它的标准:使用 WMS 请求中的 layerDefs 参数过滤要素—文档 | ArcGIS Enterpris…...

2013年108计网
第33题 在 OSI 参考模型中, 下列功能需由应用层的相邻层实现的是()A. 对话管理B. 数据格式转换C. 路由选择D. 可靠数据传输 很显然,题目所问的应用层的相邻层是表示层。该层实现与数据表示相关的功能。选项a中的对话管理属于会话层。选项c中的路由选择属于网络层。…...

【数据结构】单链表OJ题(一)
🔥博客主页: 小羊失眠啦. 🎥系列专栏:《C语言》 《数据结构》 《Linux》《Cpolar》 ❤️感谢大家点赞👍收藏⭐评论✍️ 文章目录 前言一、移除链表元素二、寻找链表中间结点三、输出链表倒数第k个结点四、反转单链表五…...

2023年云计算发展趋势浅析
云计算的概念 云计算是一种通过互联网提供计算资源和服务的模式。它允许用户通过网络访问和使用共享的计算资源,而无需拥有或管理这些资源的物理设备。云计算的核心理念是将计算能力、存储资源和应用程序提供给用户,以便随时随地根据需要…...
[极客大挑战 2019]Http1
打开题目 没有发现什么,我们查看源代码 在这里我们发现了提示 访问一下页面得到 提示说不能来自于https://Sycsecret.buuoj.cn,我们尝试访问一下这个url 发现访问不了 我们bp抓包一下 伪造个referer头 referer:https://Sycsecret.buuoj.cn 发包过去…...
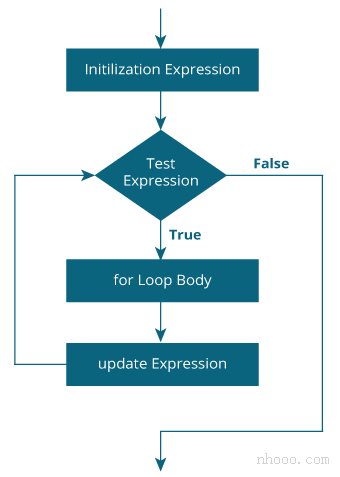
C 语言 for循环
C 语言 for循环 在本教程中,您将借助示例学习在C语言编程中创建for循环。 在编程中,循环用于重复代码块,直到满足指定条件为止。 C语言编程具有三种循环类型: for 循环while 循环do… while 循环 我们将在本教程中学习for循环…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...
