特殊矩阵的压缩存储(对称矩阵,三角矩阵,三对角矩阵,稀疏矩阵)
目录
- 1.数组的存储结构
- 1.—维数组
- 2.二维数组
- 1.行优先存储
- 2.列优先存储
- 2.特殊矩阵
- 1.对称矩阵
- 1.行优先存储
- 2.三角矩阵
- 1.上三角矩阵
- 2.下三角矩阵
- 3.三对角矩阵(带状矩阵)
- 4.稀疏矩阵
1.数组的存储结构
1.—维数组
各数组元素大小相同,且物理上连续存放。
数组元素a[i]的存放地址= 起始地址 L O C + i ∗ s i z e o f ( E l e m T y p e ) ( 0 < i < 10 ) 起始地址LOC+i * sizeof(ElemType)(0<i<10) 起始地址LOC+i∗sizeof(ElemType)(0<i<10)
2.二维数组
1.行优先存储
M行N列的二维数组b[M][N]中,若按
行优先存储,
则b[i][j]的存储地址= L O C + ( i ∗ N + j ) ∗ s i z e o f ( E l e m T y p e ) LOC + (i*N+ j) * sizeof(ElemType) LOC+(i∗N+j)∗sizeof(ElemType)
2.列优先存储
M行N列的二维数组b[M][N]中,若按
列优先存储,
则b[i][i]的存储地址= L O C + ( j ∗ M + i ) ∗ s i z e o f ( E l e m T y p e ) LOC+ ( j*M+i ) * sizeof(ElemType) LOC+(j∗M+i)∗sizeof(ElemType)
2.特殊矩阵
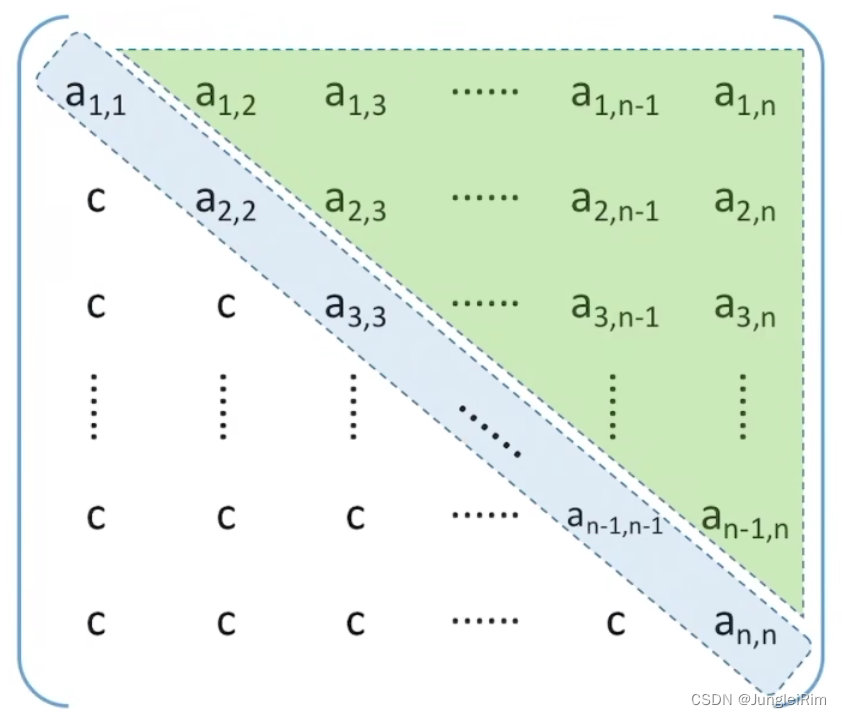
1.对称矩阵
若n阶
方阵中任意一个元素aij,都有 a i j = a j i aij=aji aij=aji则该矩阵为对称矩阵。
压缩存储策略:只存储主对角线+下三角区(或主对角线+上三角区)
1.行优先存储
1.下三角区
策略:只存储主对角线+下三角区。
①存储的数组长度: ( 1 + n ) ∗ n / 2 (1+n)*n/2 (1+n)∗n/2
②矩阵下标 a i j aij aij与一维数组下标k的映射关系: k = i ( i − 1 ) 2 + j − 1 , i > = j k=\frac{i(i-1)}{2}+j-1,i>=j k=2i(i−1)+j−1,i>=j
2.上三角区
根据对称矩阵的性质: a i j = a j i aij = aji aij=aji:
k = j ( j − 1 ) 2 + i − 1 , i < j k=\frac{j(j-1)}{2}+i-1,i<j k=2j(j−1)+i−1,i<j
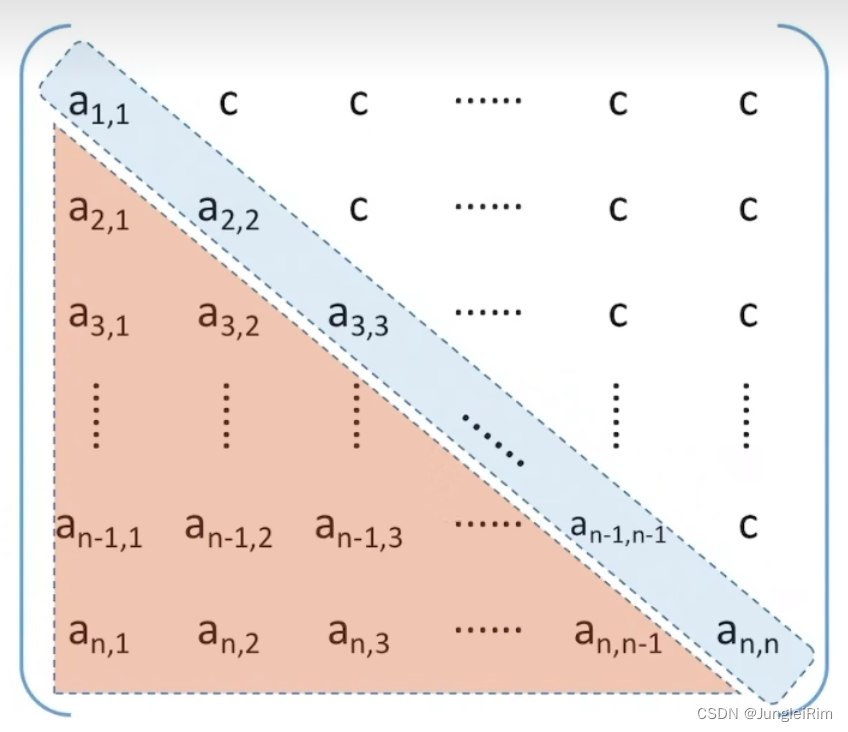
2.三角矩阵
压缩存储策略:按
行优先原则将橙色区元素存入一维数组中。并在最后一个位置存储常量c。
1.上三角矩阵
除了主对角线和上三角区,其余的元素都相同。
按照行优先的原则,映射关系: k = ( i − 1 ) ( 2 n − i + 2 ) 2 + j − i , i < = j ( 上三角区和主对角线元素 ) k=\frac{(i-1)(2n-i+2)}{2}+j-i,i<=j(上三角区和主对角线元素) k=2(i−1)(2n−i+2)+j−i,i<=j(上三角区和主对角线元素)
k = n ( n + 1 ) 2 , i > j ( 下三角区元素 ) k = \frac{n(n+1)}{2},i>j(下三角区元素) k=2n(n+1),i>j(下三角区元素)
2.下三角矩阵
除了主对角线和下三角区,其余的元素都相同。
按照行优先的原则,映射关系: k = i ( i − 1 ) 2 + j − 1 , i > = j ( 下三角区和主对角线元素 ) k=\frac{i(i-1)}{2}+j-1,i>=j(下三角区和主对角线元素) k=2i(i−1)+j−1,i>=j(下三角区和主对角线元素)
k = n ( n + 1 ) 2 , i < j ( 上三角区元素 ) k = \frac{n(n+1)}{2},i<j(上三角区元素) k=2n(n+1),i<j(上三角区元素)
3.三对角矩阵(带状矩阵)
三对角矩阵,又称
带状矩阵: 当 ∣ i − j ∣ > 1 时,有 a i j = 0 ( 1 < = i , j ≤ n ) 当|i -j|>1时,有aij=0 (1<=i, j ≤n) 当∣i−j∣>1时,有aij=0(1<=i,j≤n)
压缩存储策略:按行优先((或列优先)原则,只存储带状部分。
①已知aij求数组下标k:
前i-1行共 3 ( i − 1 ) − 1 3(i-1)-1 3(i−1)−1个元素
aij是i行第 j − i + 2 j-i+2 j−i+2个元素
aij是第 2 i + j − 2 2i+j-2 2i+j−2个元素
k = 2 i + j − 3 k=2i+j-3 k=2i+j−3(数组下标从0开始)
②若已知数组下标k,如何得到i,j?
即第k+1个元素:
i = 「 ( k + 2 ) / 3 ] i =「(k+2)/3] i=「(k+2)/3](向上取整)
由 k = 2 i + j − 3 k=2i+j-3 k=2i+j−3得,
j = k − 2 i + 3 j=k-2i+3 j=k−2i+3

4.稀疏矩阵
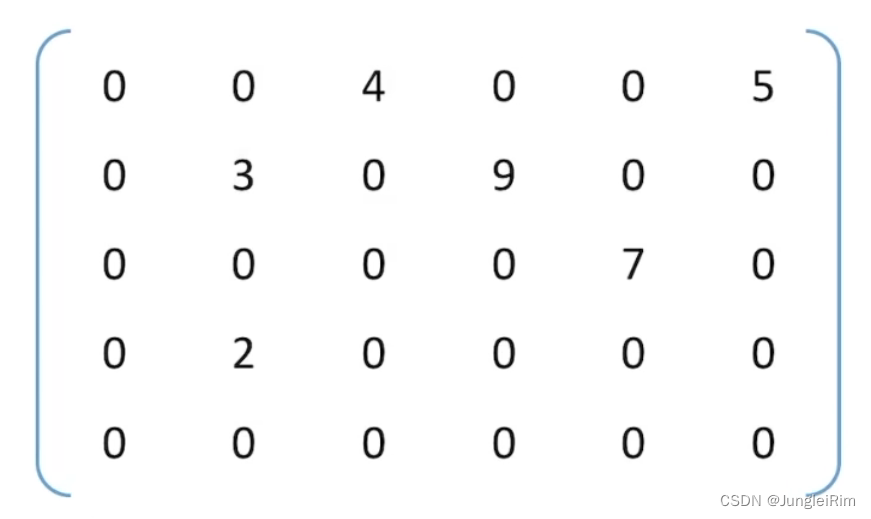
稀疏矩阵:非零元素远远少于矩阵元素的个数。
压缩存储策略:
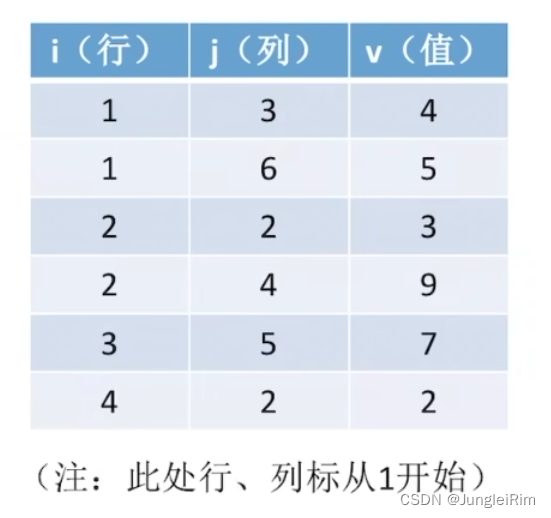
①顺序存储:三元组<行,列,值>,会失去随机存储的特性。
例如:
对应的三元组为:
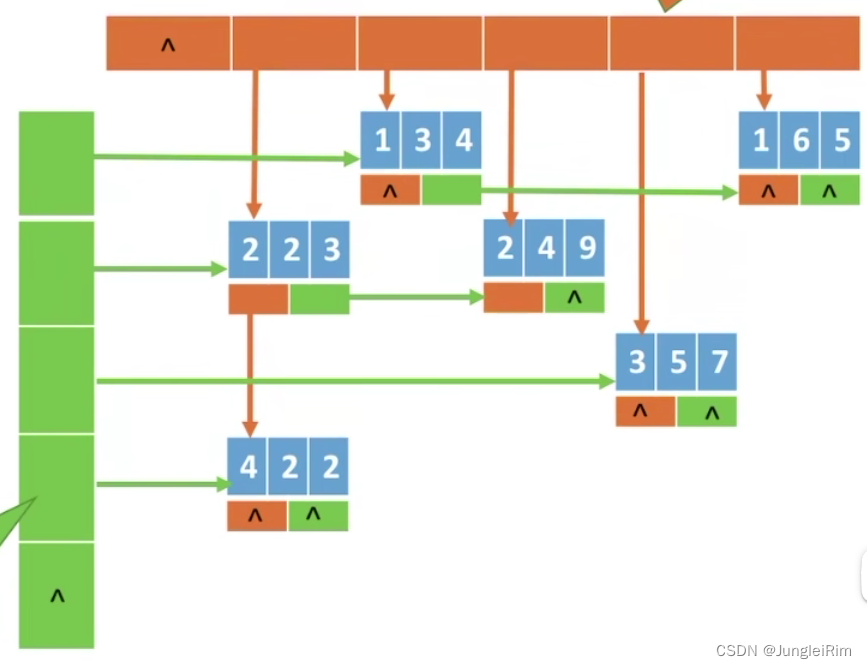
②链式存储:十字链表法
结点说明:
相关文章:
特殊矩阵的压缩存储(对称矩阵,三角矩阵,三对角矩阵,稀疏矩阵)
目录 1.数组的存储结构1.—维数组2.二维数组1.行优先存储2.列优先存储 2.特殊矩阵1.对称矩阵1.行优先存储 2.三角矩阵1.上三角矩阵2.下三角矩阵 3.三对角矩阵(带状矩阵)4.稀疏矩阵 1.数组的存储结构 1.—维数组 各数组元素大小相同,且物理上…...

DDU框架学习之路
目录 MVVM对比 DDU 数据消费者UI 数据的转换者:Domain Layer 数据图生产者/提供者 DataLayer 遵循原理: 单一数据流: Android官方推荐架构:DDU MVVM对比 M:Model 网络层 用于获取远端数据 VM:ViewModel 中间转…...
进阶课6——基于Seq2Seq的开放域生成型聊天机器人的设计和开发流程
情感聊天机器人通常属于开放领域,用户可以与机器人进行各种话题的互动。例如,微软小冰和早期的AnswerBus就是这种类型的聊天机器人。基于检索的开放领域聊天机器人需要大量的语料数据,其开发流程与基于任务型的聊天机器人相似,而基…...

Java面试题04
1.Array 和 ArrayList 有何区别? Array是固定长度的,元素类型可以是基本类型,创建后大小不可改变;ArrayList是可变长 度的,只能存储对象,可以动态添加和删除元素。 区别1: 存储类型不同 …...
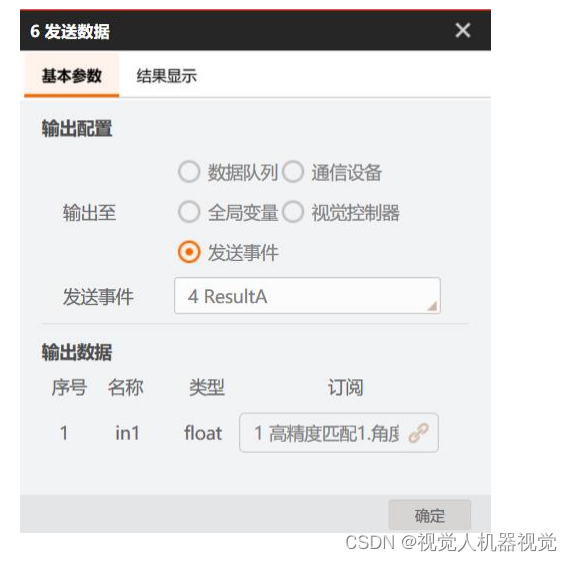
海康Visionmaster-通讯管理:使用 Modbus TCP 通讯 协议与流程交互
使用 Modbus TCP 通讯协议与视觉通讯,当地址为 0000 的保持型寄存器(4x 寄存器)变为 1 时,触发视觉流程执行一次,同时视觉将地址为 0000 的寄存器复位(也即写为 0),视觉流程执行完成后,将结果数…...

assimp中如何判断矩阵是否是单位矩阵
对于一个矩阵元素为浮点型的矩阵,你是否还在使每个元素跟1.0f或0.0f进行比较,如果这样,只能说你的结果不一定正确,那我们看看assimp中是如何做的。 template <typename TReal> AI_FORCE_INLINE bool aiMatrix4x4t<TReal…...

大数据Doris(二十):数据导入(Broker Load)介绍
文章目录 数据导入(Broker Load)介绍 一、适用场景...

Docker快速安装kafka
创建zk docker run -d --name zookeeper-server \-e ALLOW_ANONYMOUS_LOGINyes \bitnami/zookeeper:latest创建kafka docker run -d --name kafka-server \-p 9092:9092 \-e ALLOW_PLAINTEXT_LISTENERyes \-e KAFKA_CFG_ZOOKEEPER_CONNECTzookeeper-server:2181 \-e KAFKA_CF…...
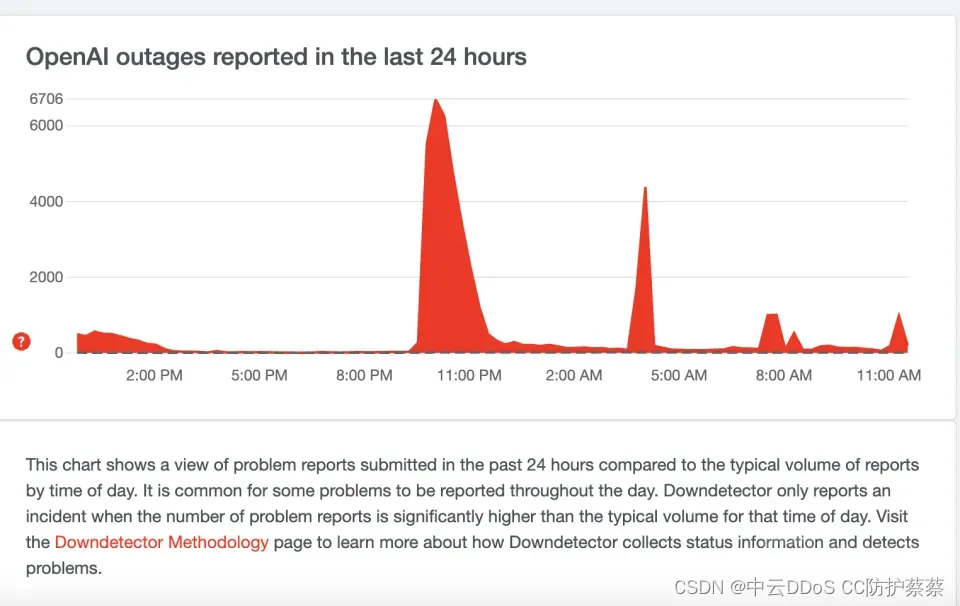
ChatGPT是什么?黑客试图淹没其服务
上线2个月,月活跃用户破亿,媒体人用它编辑文案,学生用它写作业,程序员用它编辑代码, 它是谁呢? 它就是火爆全网(chatgpt),chatgpt是什么呢,chatgpt是美国研发的一款人工…...

【Java 进阶篇】Java Web 开发之 Listener 篇:ServletContextListener 使用详解
欢迎大家来到 Java Web 开发的学习之旅!在前面的博客中,我们已经学习了 Servlet、JSP、Filter 等重要的概念和技术。今天,我们将深入探讨 Java Web 开发中另一个重要的组成部分——Listener(监听器),具体来…...

[C/C++]数据结构 链表OJ题:环形链表(如何判断链表是否有环)
题目描述: 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置&…...

c#流程控制
c#分支语句 namespace ConsoleApp1 {internal class Program{static void Main(string[] args){Console.WriteLine("请输入学生成绩");string sConsole.ReadLine();int aint.Parse(s);//将字符类型强制转换为int类型if (a > 90){ Console.WriteLine("成绩优…...

基于SSM的学生二手书籍交易平台的设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

xcode-工程设置
build settings Deployment Postprocessing 用于指定是否在构建完成后进行一些部署相关的处理。 当你在 Xcode 中构建你的应用程序时,构建设置决定了一些行为,其中一项是是否启用 Deployment Postprocessing。这个选项的主要作用是在构建完成后&#…...
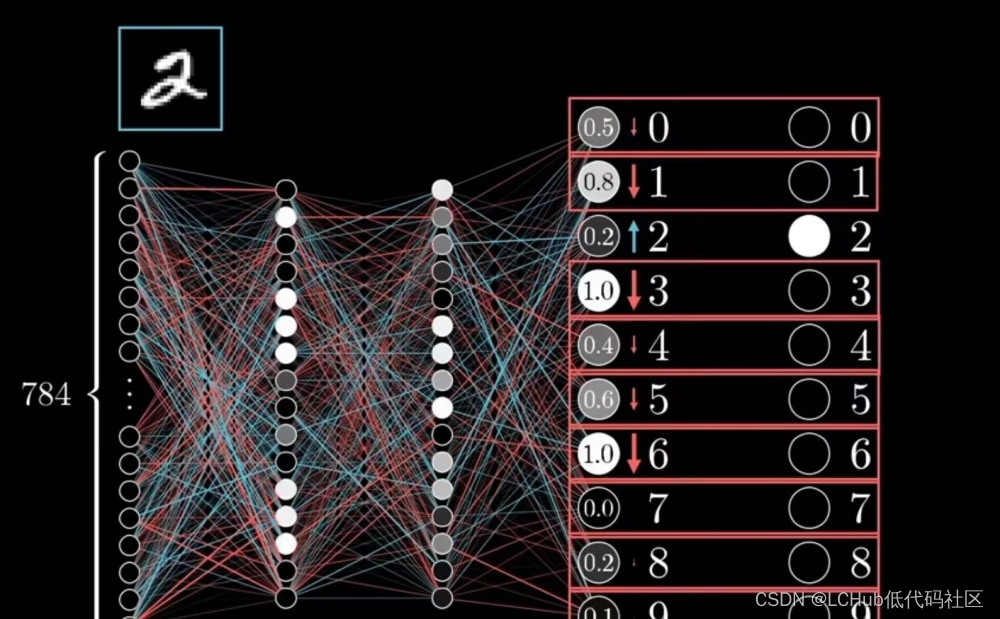
Milvus Cloud——LLM Agent 现阶段出现的问题
LLM Agent 现阶段出现的问题 由于一些 LLM(GPT-4)带来了惊人的自然语言理解和生成能力,并且能处理非常复杂的任务,一度让 LLM Agent 成为满足人们对科幻电影所有憧憬的最终答案。但是在实际使用过程中,大家逐渐发现了通…...

百度智能云千帆大模型平台再升级,SDK版本开源发布!
SDK 前言一、SDK的优势二、千帆SDK:快速落地LLM应用三、如何快速上手千帆SDK1、SDK快速启动快速安装平台鉴权如何获取AK/SK以“Chat 对话”为调用示例 2. SDK进阶指引3. 通过Langchain接入千帆SDK为什么选择Langchain 开源社区 前言 百度智能云千帆大模型平台再次升…...

按键精灵中的数据类型转换
按键精灵中的数据类型有:整型、浮点数、布尔类型、字符串、数组这几种类型,主要的转换方式有以下这几种方式: 1. 转布尔类型 CBool Dim A 5 Dim B CBool(A)TracePrint B // true 2. 转字符串类型 CStr Dim MyInteger 437Dim MyStr…...

Golang Gorm 连接数据库
连接数据库 为了连接数据库,你首先要导入数据库驱动程序。例如: import _ "github.com/go-sql-driver/mysql"import ("gorm.io/driver/mysql""gorm.io/gorm" ) GORM 已经包含了一些驱动程序,为了方便的去记住…...
[C++随笔录] 红黑树
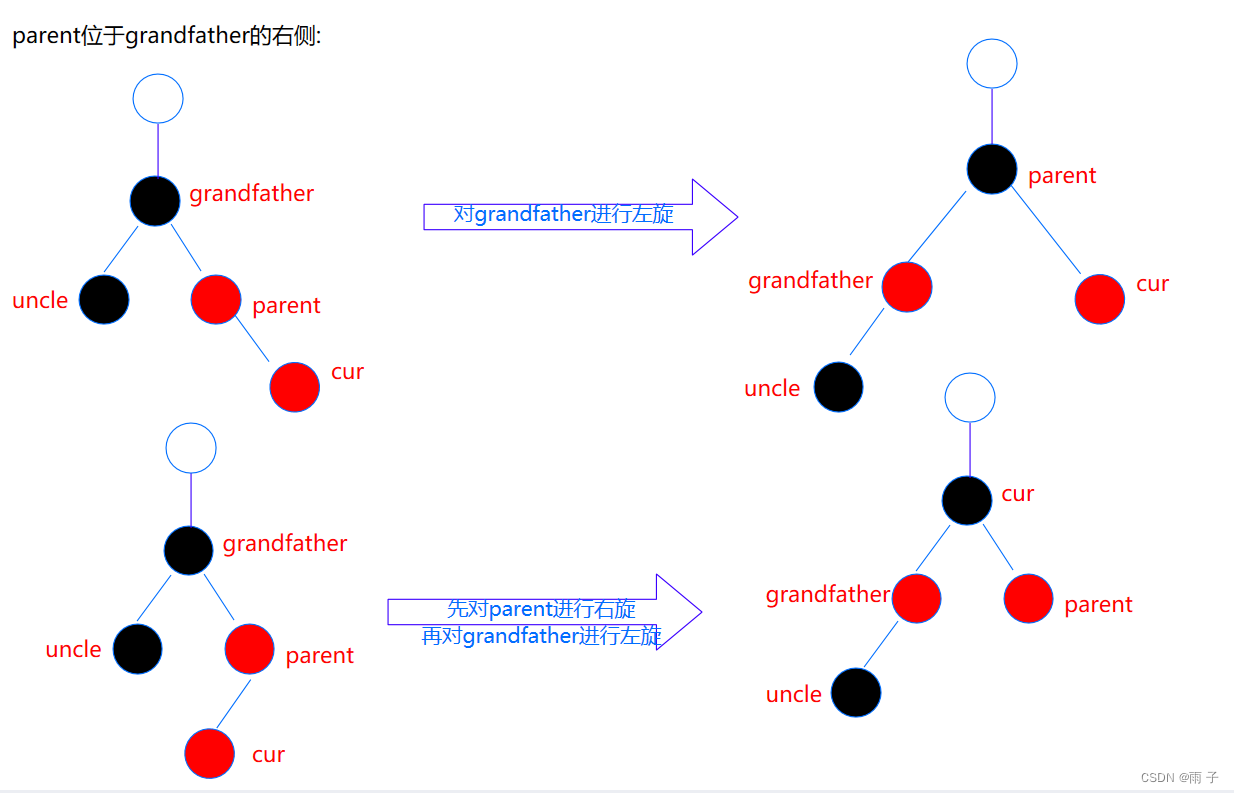
红黑树 红黑树的特点红黑树的模拟实现红黑树的底层结构insert的实现实现思路更新黑红比例的逻辑insert的完整代码 insert的验证 源码 红黑树的特点 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是 Red或 Black。…...

C 和 C++ 可变参数介绍
文章目录 前言概念C 的可变参数参数列表 #va_list 4组宏 C 的可变参数参数列表 #va_list 4组宏初始化列表 initializer_list<> 类模板可变参数模板 总结参考资料作者的话 前言 C 和 C 可变参数介绍。 概念 可变(长)/不定(长ÿ…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...