[C++随笔录] 红黑树
红黑树
- 红黑树的特点
- 红黑树的模拟实现
- 红黑树的底层结构
- insert的实现
- 实现思路
- 更新黑红比例的逻辑
- insert的完整代码
- insert的验证
- 源码
红黑树的特点
-
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是
Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的. -
红黑树的特点:
- 节点颜色不是红色就是黑色
- 根节点是黑色的
- 每一条路径的黑色节点数目是相同的, (注意:
这里的路径是从根节点到NIL(黑色)节点) - 每一条路径不允许出现连续的红色节点
-
路径是从根节点 到 NIL节点的

🗨️满足上面的条件, 为啥就能保证 红黑树确保没有一条路径会比其他路径长出俩倍呢?
- 根据上述的特点, 我们可以得知:
当每条路径的黑色节点数目一定的情况下, 最短路径是全黑, 最长路径是黑红相间的
如果我们保证最长路径 不超过 最短路径的二倍就可以了

红黑树的模拟实现
红黑树的底层结构
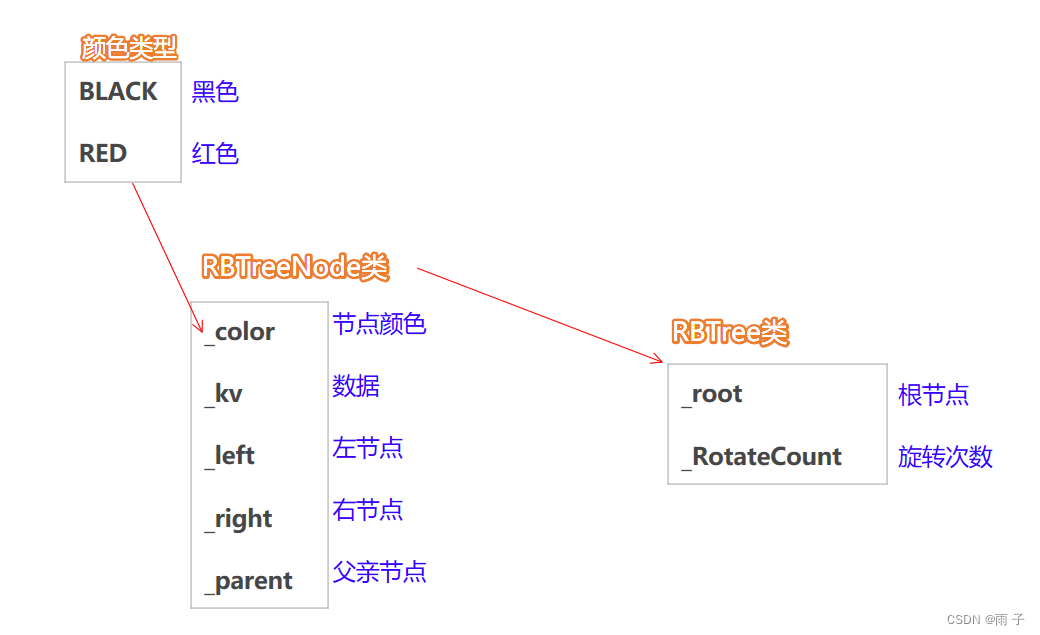
- 颜色类型
// 枚举
enum Color
{RED,BLACK
};
- RBTreeNode类
template<class K, class V>
struct RBTreeNode
{
public:RBTreeNode(const pair<K, V> kv):_kv(kv){}public:pair<K, V> _kv;Color _color = BLACK;RBTreeNode<K, V>* _left = nullptr;RBTreeNode<K, V>* _right = nullptr;RBTreeNode<K, V>* _parent = nullptr;
};
- RBTree类
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;public:RBTree(){}private:// 根节点Node* _root = nullptr;// 记录旋转次数int RotateCount = 0;
}
insert的实现
实现思路
二叉搜索树的插入逻辑 + 更新黑红比例
bool Insert(const pair<K, V> kv)
{if (_root == nullptr){// 根节点是黑色的_root = new Node(kv);_root->_color = BLACK;return true;}Node* parent = _root;Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 新建一个节点, 默认是红色cur = new Node(kv);cur->_color = RED;// 链接cur 和 parentif (cur->_kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 更改黑红比例// ...// ...// 更新完黑红比例后, 就返回truereturn true;
}
🗨️ 不能出现连续的红色节点 ⇒ 我们插入节点给个黑色节点多好, 为啥还要给红色节点冒风险呢?
因为, 我们插入的节点颜色是 红色, 插入的位置就有两种可能:
- 插入到黑色节点的后面 — — 正常的情况, 不需要进行更新
- 插入到红色节点的后面 — — 出现连续的红色节点, 需要
更新这一条支路 (当前节点到祖宗节点这一条路径)中的黑红比例
更新黑红比例的逻辑
由于 插入前, 是符合红黑树的性质,
插入的节点是红色 ⇒ 插入后才会出现连续的红色节点
⇒ 设插入的新节点为 cur(红色) ,
则父亲节点 paren 为 红色, 祖父节点 grandfather 为 黑色 ⇒ 这才符合 插入前符合红黑树的特点, 插入后才会出现连续的红色节点的情况
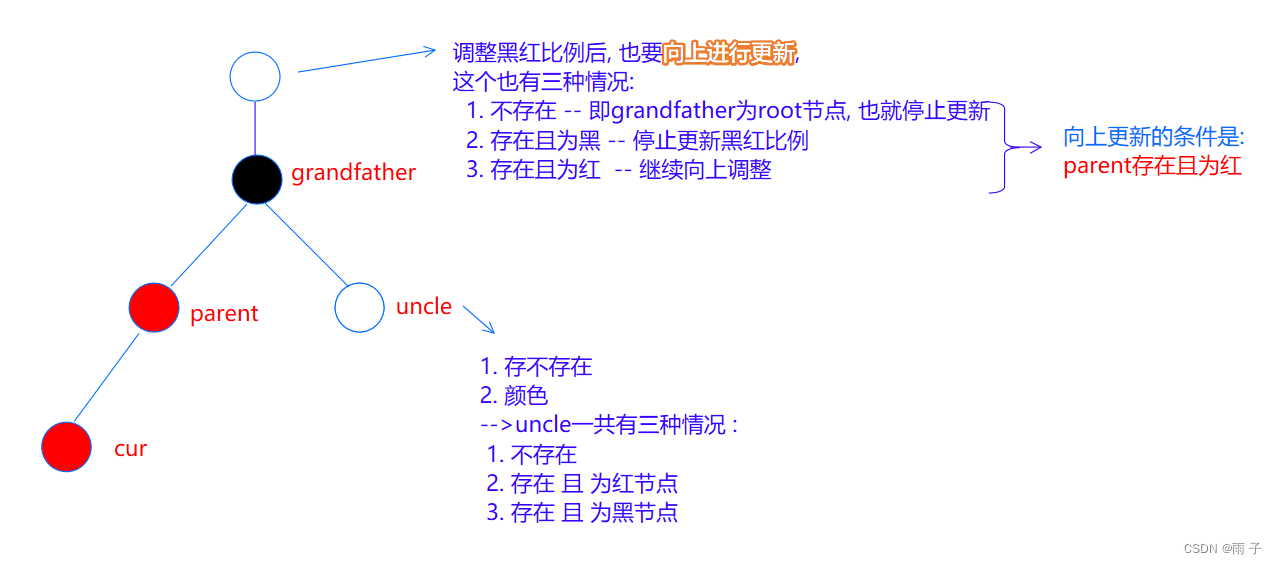
其实, 更新 当前节点到 祖宗节点这一条路径的 黑红比例 的本质是 看uncle的情况
首先, 要确定 uncle 位于grandfather的哪一侧 && uncle不一定存在, 但parent一定存在
⇒ 要确定parent 位于 grandfather的那一侧:
- parent 位于 grandfather的左侧
- parent 位于 grandfather的右侧
其次, 才是 uncle 的存在情况 以及 颜色情况
-
uncle存在且为红

-
uncle不存在
如果 uncle不存在 ⇒cur为新增节点
- 如果cur不是新增节点, 那么 parent后面的节点必定是黑色的, 那么就违反了
每一条路径的黑色节点的个数是相同

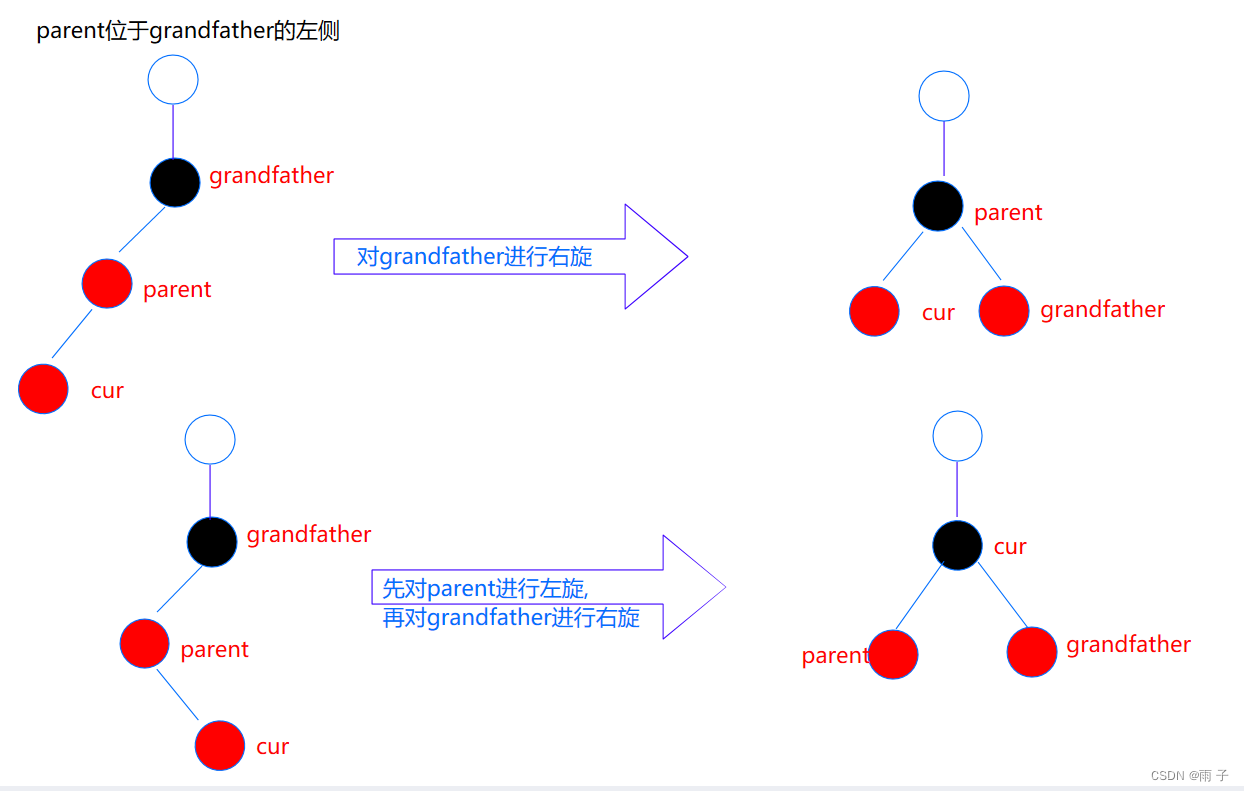

- uncle存在且为黑

如果uncle存在, 那么必定是黑色⇒ 那么 cur 也应该是黑色.
现在看到的cur 是红色的, 是由下面的更新上来的
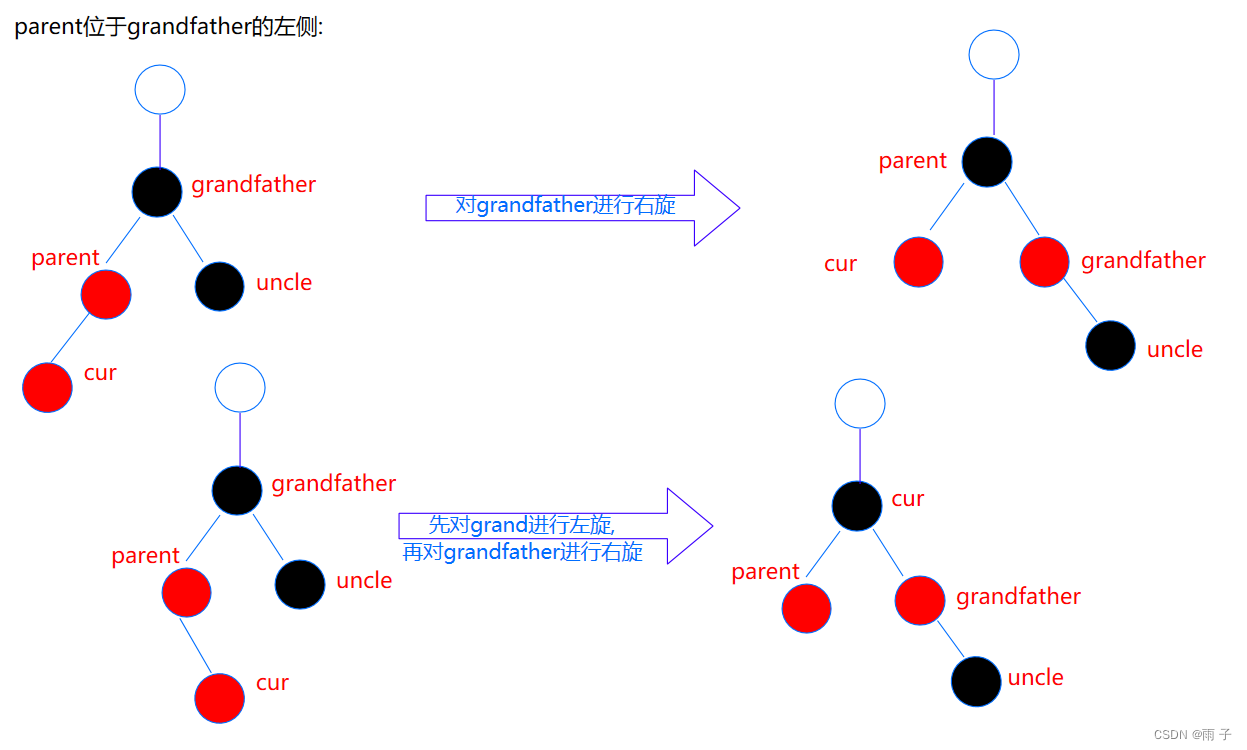
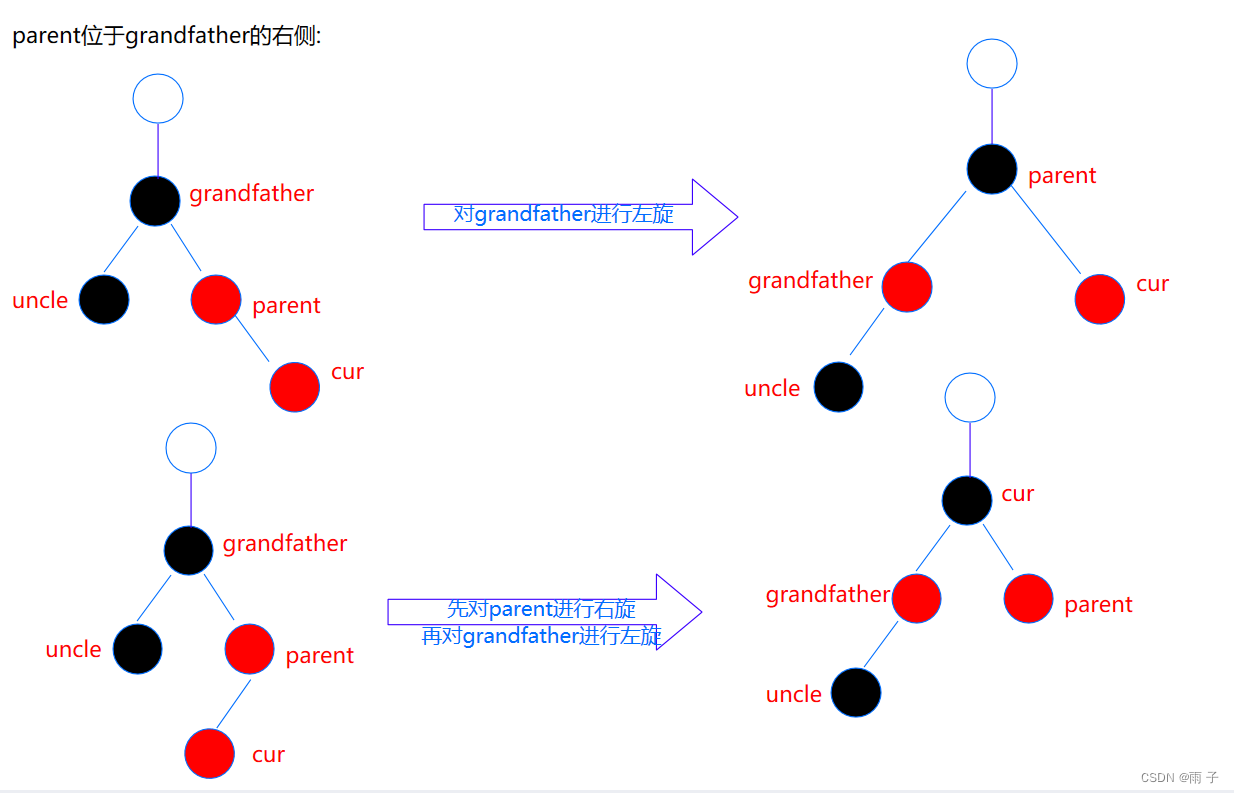
通过上面的图示, 我们得出 : 插入时, uncle主要分为两种情况
- uncle存在且为红 — —
由于更新后的头结点为红 ⇒ 我们需要继续向上更新下去 - uncle不存在 或 uncle存在且为黑 — —
由于更新后的头结点为黑 ⇒ 我们不需要继续向上更新下去
insert的完整代码
bool Insert(const pair<K, V> kv)
{if (_root == nullptr){// 根节点是黑色的_root = new Node(kv);_root->_color = BLACK;return true;}Node* parent = _root;Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 新建一个节点, 默认是红色cur = new Node(kv);cur->_color = RED;// 链接cur 和 parentif (cur->_kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 更改黑红比例// 父亲节点存在且为红, 才有机会继续向上更新下去while (parent && parent->_color == RED){Node* grandfather = parent->_parent;// parent 为 grandfather的左侧if (grandfather->_left == parent){Node* uncle = grandfather->_right;// u存在且为红if (uncle && uncle->_color == RED){// 颜色变化grandfather->_color = RED;parent->_color = uncle->_color = BLACK;// 继续向上调整cur = grandfather;parent = cur->_parent;}else // u不存在 或 u存在且为黑色{if (cur == parent->_left){RotateR(grandfather);grandfather->_color = RED;parent->_color = BLACK;}else{RotateL(parent);RotateR(grandfather);cur->_color = BLACK;grandfather->_color = RED;}// 更新后的头节点为黑色, 不需要继续向上更新break;}}// parent 为 grandfather的右侧else if (grandfather->_right == parent){Node* uncle = grandfather->_left;// u存在且为红if (uncle && uncle->_color == RED){// 颜色变化grandfather->_color = RED;uncle->_color = parent->_color = BLACK;// 继续向上调整cur = grandfather;parent = cur->_parent;}// u不存在 或 u存在且为黑色else{if (parent->_right == cur){RotateL(grandfather);parent->_color = BLACK;grandfather->_color = RED;}else{RotateR(parent);RotateL(grandfather);cur->_color = BLACK;grandfather->_color = RED;}// 更新后的头节点为黑色, 不需要继续向上更新break;}}else{assert("黑红比例失控!");}}// 有可能更新过程中会把 root更新为红色 // && root节点的颜色必须为黑色// -->暴力统一处理根节点的颜色_root->_color = BLACK;return true;
}
insert的验证
- 每一条路径的
黑节点个数相同⇒先找一个 基准值(root的左子树中 黑节点的个数)
如果后面的路径中 有的黑节点的个数 跟 基准值不同, 那就返回false. - 不能有连续的红节点 ⇒
当前节点为红节点, 那么父亲节点不能为红节点 root节点的颜色要为黑色
验证代码
// 外面调用接口
bool IsBalance()
{return IsBalance(_root);
}bool IsBalance(Node* root)
{if (root == nullptr)return true;// root节点为红, 就直接返回falseif (root->_color != BLACK){return false;}// 基准值 -- root左子树中的黑节点个数int benchmark = 0;Node* cur = _root;while (cur){if (cur->_color == BLACK)++benchmark;cur = cur->_left;}// 检查每条路径中黑节点个数 && 不能出现连续的红节点return CheckColour(root, 0, benchmark);
}bool CheckColour(Node* root, int blacknum, int benchmark)
{// 到叶子节点, 比较路径中黑节点的个数 和 基准值if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_color == BLACK){++blacknum;}// 不能存在连续的红节点if (root->_color == RED && root->_parent && root->_parent->_color == RED){cout << root->_kv.first << "出现连续红色节点" << endl;return false;}return CheckColour(root->_left, blacknum, benchmark)&& CheckColour(root->_right, blacknum, benchmark);
}
Height
// 外面调用接口
int Height()
{return Height(_root);
}int Height(Node* root)
{if (root == nullptr)return 0;int left = Height(root->_left);int right = Height(root->_right);return left > right ? left + 1 : right + 1;
}
GetRotateCount
int GetRoateCount()
{return RotateCount;
}
测试程序
void rbt_test()
{const int N = 10000000;vector<int> v;v.reserve(N);srand((unsigned int)time(NULL));for (size_t i = 0; i < N; i++){int ret = rand();v.push_back(ret);// v.push_back(i);}muyu::RBTree<int, int> rbt;for (auto e : v){rbt.Insert(make_pair(e, e));// cout << "Insert:" << e << "->" << avl.Isbalance() << endl;}cout << "红黑树是否达标-> " << rbt.IsBalance() << endl;cout << "红黑树的高度-> " << rbt.Height() << endl;cout << "红黑树旋转的次数-> " << rbt.GetRoateCount() << endl;
}int main()
{rbt_test();return 0;
}
运行结果:
红黑树是否达标-> 1
红黑树的高度-> 19
红黑树旋转的次数-> 19119
源码
#pragma once#include<iostream>using namespace std;namespace muyu
{// 枚举enum Color{RED,BLACK};template<class K, class V>struct RBTreeNode{public:RBTreeNode(const pair<K, V> kv):_kv(kv){}public:pair<K, V> _kv;Color _color = BLACK;RBTreeNode<K, V>* _left = nullptr;RBTreeNode<K, V>* _right = nullptr;RBTreeNode<K, V>* _parent = nullptr;};template<class K, class V>class RBTree{typedef RBTreeNode<K, V> Node;public:RBTree(){}void RotateL(Node* parent){++RotateCount;Node* cur = parent->_right;Node* grandfather = parent->_parent;Node* curleft = cur->_left;// 旋转核心parent->_right = curleft;cur->_left = parent;// 更新父亲// 1. parent && curleftif (curleft){curleft->_parent = parent;}parent->_parent = cur;// 2.更新curif (grandfather == nullptr){cur->_parent = nullptr;_root = cur;}else{if (grandfather->_left == parent){grandfather->_left = cur;}else{grandfather->_right = cur;}cur->_parent = grandfather;}}void RotateR(Node* parent){++RotateCount;Node* cur = parent->_left;Node* grandfather = parent->_parent;Node* curright = cur->_right;// 旋转核心parent->_left = curright;cur->_right = parent;// 更新链接关系// 1. parent && currightif (curright){curright->_parent = parent;}parent->_parent = cur;// 2.更新curif (grandfather == nullptr){cur->_parent = nullptr;_root = cur;}else{if (grandfather->_left == parent){grandfather->_left = cur;}else{grandfather->_right = cur;}cur->_parent = grandfather;}}bool Insert(const pair<K, V> kv){if (_root == nullptr){// 根节点是黑色的_root = new Node(kv);_root->_color = BLACK;return true;}Node* parent = _root;Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 新建一个节点, 默认是红色cur = new Node(kv);cur->_color = RED;// 链接cur 和 parentif (cur->_kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 更改黑红比例while (parent && parent->_color == RED){Node* grandfather = parent->_parent;if (grandfather->_left == parent){Node* uncle = grandfather->_right;// u存在且为红if (uncle && uncle->_color == RED){// 颜色变化grandfather->_color = RED;parent->_color = uncle->_color = BLACK;// 继续向上调整cur = grandfather;parent = cur->_parent;}else // u不存在 或 u存在且为黑色{if (cur == parent->_left){RotateR(grandfather);grandfather->_color = RED;parent->_color = BLACK;}else{RotateL(parent);RotateR(grandfather);cur->_color = BLACK;grandfather->_color = RED;}break;}}else if (grandfather->_right == parent){Node* uncle = grandfather->_left;// u存在且为红if (uncle && uncle->_color == RED){// 颜色变化grandfather->_color = RED;uncle->_color = parent->_color = BLACK;// 继续向上调整cur = grandfather;parent = cur->_parent;}// u不存在 或 u存在且为黑色else{if (parent->_right == cur){RotateL(grandfather);parent->_color = BLACK;grandfather->_color = RED;}else{RotateR(parent);RotateL(grandfather);cur->_color = BLACK;grandfather->_color = RED;}break;}}else{assert("黑红比例失控!");}}// 暴力统一处理根节点的颜色_root->_color = BLACK;return true;}int Height(){return Height(_root);}int Height(Node* root){if (root == nullptr)return 0;int left = Height(root->_left);int right = Height(root->_right);return left > right ? left + 1 : right + 1;}bool CheckColour(Node* root, int blacknum, int benchmark){if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_color == BLACK){++blacknum;}if (root->_color == RED && root->_parent && root->_parent->_color == RED){cout << root->_kv.first << "出现连续红色节点" << endl;return false;}return CheckColour(root->_left, blacknum, benchmark)&& CheckColour(root->_right, blacknum, benchmark);}bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr)return true;if (root->_color != BLACK){return false;}// 基准值int benchmark = 0;Node* cur = _root;while (cur){if (cur->_color == BLACK)++benchmark;cur = cur->_left;}return CheckColour(root, 0, benchmark);}int GetRoateCount(){return RotateCount;}private:Node* _root = nullptr;int RotateCount = 0;};
}
十年磨一剑,霜刃未曾试。
今日把示君,谁有不平事。
— — 贾岛《剑客》
相关文章:

[C++随笔录] 红黑树
红黑树 红黑树的特点红黑树的模拟实现红黑树的底层结构insert的实现实现思路更新黑红比例的逻辑insert的完整代码 insert的验证 源码 红黑树的特点 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是 Red或 Black。…...

C 和 C++ 可变参数介绍
文章目录 前言概念C 的可变参数参数列表 #va_list 4组宏 C 的可变参数参数列表 #va_list 4组宏初始化列表 initializer_list<> 类模板可变参数模板 总结参考资料作者的话 前言 C 和 C 可变参数介绍。 概念 可变(长)/不定(长ÿ…...
【Git】gui图形化界面的使用、ssh协议以及idea集成Git
目录 gui图形化界面的使用 介绍 特点 gui图形的使用 ssh协议 介绍 步骤及概念 ssh协议的使用 配置公钥 idea集成Git idea配置git IDEA安装gitee IDEA中登入Git 编辑 项目分享 克隆分享的项目 编辑 编辑 idea上传远程 gui图形化界面的使用 介绍 GUI(…...
C语言之文件操作(详解版)
不知不觉我们已经学到C语言的文件操作部分了,这部分内容其实很有意思,因为它可以直接把我们代码中的数据写入硬盘,而不是我们关掉这个程序,代码就没有了,让我们开始学习吧! 目录 1.为什么使用文件 2.什么…...

解决mac 下 docker-compose 不是命令
docker-compose docker: ‘compose’ is not a docker command #6569 解决方法: mkdir -p /usr/local/lib/docker ln -s /Applications/Docker.app/Contents/Resources/cli-plugins /usr/local/lib/docker/cli-plugins参考: https://github.com/docker/…...

test_sizeof
test_sizeof //结论: // sizeof(arrU8)得到的大小是u8类型数组的 **定义大小**,在 初始化的时候用 // strlen(arrU8)得到的大小是u8类型数组的 **实际大小**,在 复制的时候用 //sizeof((char*)arrU8),把一个u8 * 转成 char *&…...

100+ Windows运行命令大全,装B高手必备
操作电脑关闭、重启、注销、休眠的命令细则: 用法: shutdown [/i | /l | /s | /sg | /r | /g | /a | /p | /h | /e | /o] [/hybrid] [/soft] [/fw] [/f] [/m \\computer][/t xxx][/d [p|u:]xx:yy [/c "comment"]] 没有参数 显示帮助。这与键入 /? 是一样的。…...
iOS 设置图标和upload包时显示错误
右键-show in finder-AppIcon.appiconset-然后替换图片 然后遇到个问题 就是图片不能有alpha [Xcode]应用图标:ERROR ITMS-90717: “Invalid App Store Icon. The App Store Icon in the asset catalog in x… 具体操作:只需确保【AppIcon】图片集中不…...

软件工程的舞台上,《人月神话》的美学纷飞
前言: Hello大家好,我是Dream。 今天给大家分享一本书:《人月神话》——软件工程的经典之作。 《人月神话》是一本具有深远影响力的软件工程著作,无论是软件开发者、管理者还是学习软件工程的人士,都能从中获得宝贵的启…...
笔记——程序设计)
C现代方法(第19章)笔记——程序设计
文章目录 第19章 程序设计19.1 模块19.1.1 内聚性与耦合性19.1.2 模块的类型 19.2 信息隐藏19.2.1 栈模块 19.3 抽象数据类型19.3.1 封装19.3.2 不完整类型 19.4 栈抽象数据类型19.4.1 为栈抽象数据类型定义接口19.4.2 用定长数组实现栈抽象数据类型19.4.3 改变栈抽象数据类型中…...
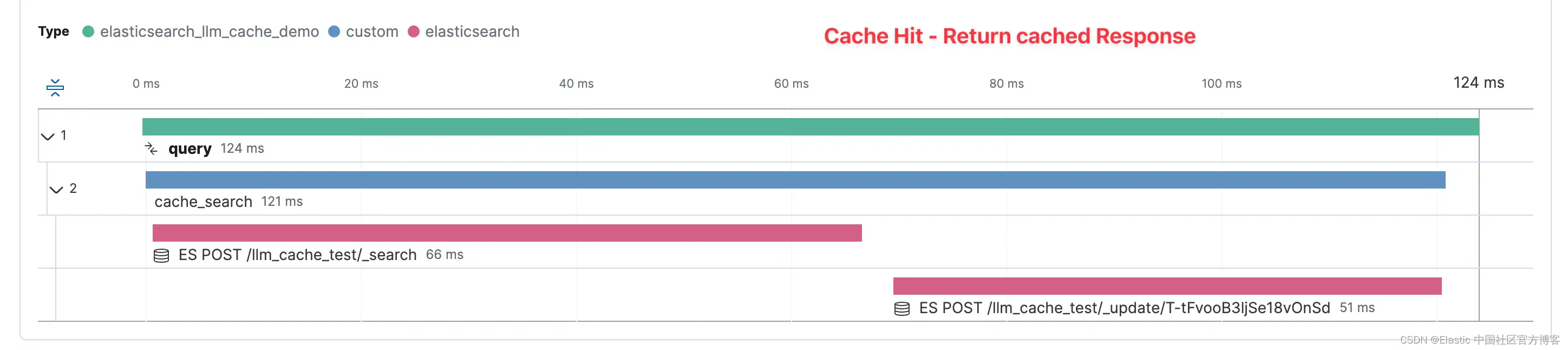
Elasticsearch 作为 GenAI 缓存层
作者:JEFF VESTAL,BAHA AZARMI 探索如何将 Elasticsearch 集成为缓存层,通过降低 token 成本和响应时间来优化生成式 AI 性能,这已通过实际测试和实际实施进行了证明。 随着生成式人工智能 (GenAI) 不断革新从客户服务到数据分析…...
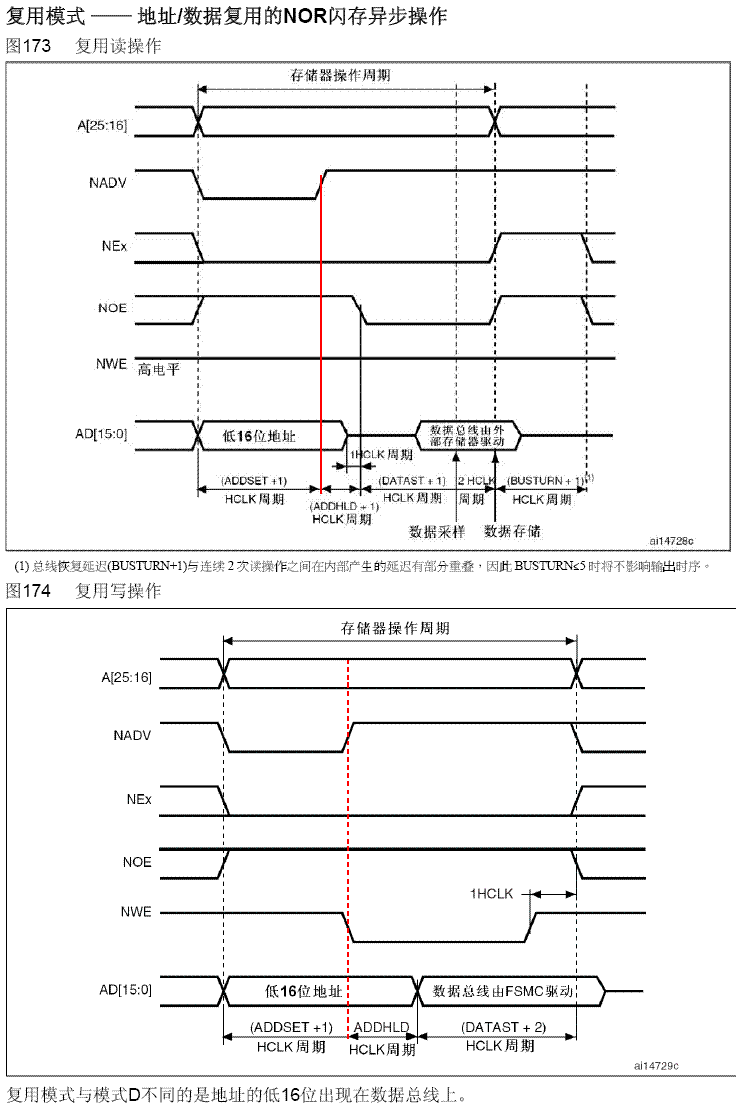
FPGA与STM32_FSMC总线通信实验
FPGA与STM32_FSMC总线通信实验 内部存储器IP核的参数设置创建IP核FPGA代码STM32标准库的程序 STM32F407 上自带 FSMC 控制器,通过 FSMC 总线的地址复用模式实现STM32 与 FPGA 之间的通信,FPGA 内部建立 RAM 块,FPGA 桥接 STM32 和 RAM 块&…...

maven配置自定义下载路径,以及阿里云下载镜像
1.配置文件 <?xml version"1.0" encoding"UTF-8"?> <settings xmlns"http://maven.apache.org/SETTINGS/1.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance" xsi:schemaLocation"http://maven.apache.org…...

01.单一职责原则
单一职责原则 概述 简单来说就是一个类只描述一件事, 比如我们熟知的 userDao.java 只负责 用户域功能。如果userDao既操作user表又操作order表,这显然不合理。正确的做法是让orderDao.java去操作order表。 对类来说的,一个类应该只负责一项…...

RT-Thread上部署TinyMaix推理框架,使MCU赋予AI能力
概要 当谈到微控制器(MCU)和人工智能(AI)的结合,我们进入了一个激动人心的领域。传统上,AI应用程序需要大型计算机或云服务器的处理能力,但随着技术的发展,现在可以将AI嵌入到微控制器中。这为嵌入式系统、物联网设备、机器人和各种其他应用开启了新的可能性。 MCU A…...
)
设计模式 -- 策略模式(Strategy Pattern)
策略模式:一种行为型模式,这些设计模式特别关注对象之间的通信。在策略模式中,我们创建表示各种策略的对象和一个行为随着策略对象改变而改变的 context 对象。策略对象改变 context 对象的执行算法。 介绍 意图:定义一系列的算…...
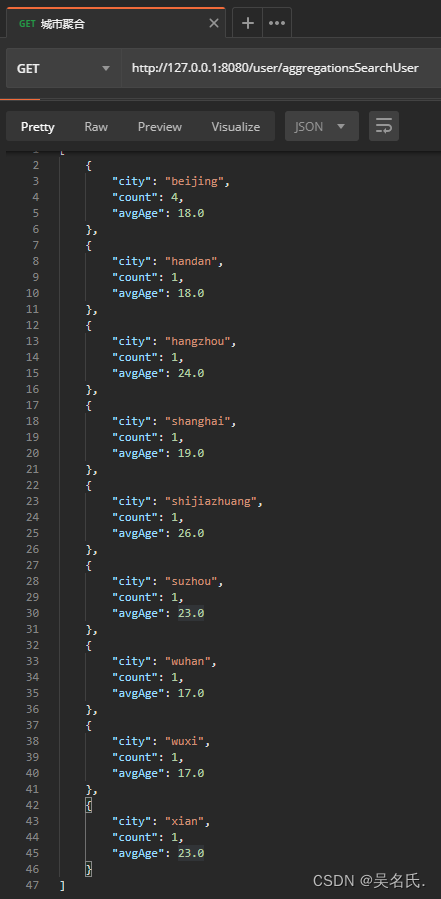
Spring Boot 集成 ElasticSearch
1 加入依赖 首先创建一个项目,在项目中加入 ES 相关依赖,具体依赖如下所示: <dependency><groupId>org.elasticsearch</groupId><artifactId>elasticsearch</artifactId><version>7.1.0</version&g…...

百度智能云正式上线Python SDK版本并全面开源!
文章目录 1. SDK的优势2. 千帆SDK:快速落地LLM应用3. 如何快速上手千帆SDK3.1 SDK快速启动3.2 SDK进阶指引3.3 通过Langchain接入千帆SDK 4. 开源社区 百度智能云千帆大模型平台再次升级!在原有API基础上,百度智能云正式上线Python SDK&#…...
LeetCode(3)删除有序数组中的重复项【数组/字符串】【简单】
目录 1.题目2.答案3.提交结果截图 链接: 26. 删除有序数组中的重复项 1.题目 给你一个 非严格递增排列 的数组 nums ,请你** 原地** 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保…...

前端视角中的微信登录
目录 引入 流程介绍 具体实现 引入 本文主要讲解网站应用中微信登录的具体流程是怎么样的,以及作为前端开发人员在这整个流程中的主要任务是什么。 如果想要实现微信登录的功能,需要开发人员到微信开放平台注册相应的账号,进行注册应用&am…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

