MapReduce编程——矩阵乘法(Python版本)
数据格式
- 对于矩阵元素 A i j A_{ij} Aij,将其处理为 < i , j , M a t r i x N a m e , v a l u e > <i,j,MatrixName,value> <i,j,MatrixName,value>的四元组格式,例如矩阵[[2, 1, 3, 4], [10, -8, 7, 2], [9, 1, 6, -2]]可被转化为如下形式
1 1 A 2 1 2 A 1 1 3 A 3 1 4 A 4 2 1 A 10 2 2 A -8 2 3 A 7 2 4 A 2 3 1 A 9 3 2 A 1 3 3 A 6 3 4 A -2
程序说明
- 假设有矩阵 A m × q A_{m \times q} Am×q与 B q × n B_{q \times n} Bq×n相乘,且矩阵 A A A与 B B B都被转化为了以上格式存储在一个txt文件中
Map函数
- Map函数接收一个四元组 < i , j , M a t r i x N a m e , v a l u e > <i,j,MatrixName,value> <i,j,MatrixName,value>作为输入,对于 A i j A_{ij} Aij返回键值对 < < i , k > , < A , j , v a l u e > > ( k = 1 , 2 , 3 , . . . , n ) <<i,k>,<A,j,value>>(k=1,2,3,...,n) <<i,k>,<A,j,value>>(k=1,2,3,...,n);对于 B i j B_{ij} Bij返回键值对 < < k , j > , < B , i , v a l u e > > ( k = 1 , 2 , 3 , . . . , m ) <<k,j>,<B,i,value>>(k=1,2,3,...,m) <<k,j>,<B,i,value>>(k=1,2,3,...,m)
Reduce函数
- Reduce函数接收shuffle后得到的键值对 < < i , k > , < < 来自 A 的第 i 行 > , < 来自 B 的第 k 列 > > > <<i,k>,<<来自A的第i行>,<来自B的第k列>>> <<i,k>,<<来自A的第i行>,<来自B的第k列>>>,此时只需使得A与B中对应的元素相乘再相加即可得到结果 C i j C_{ij} Cij
代码
# 文件命名为matmul.py,矩阵数据写在matrix.txt文件中
from mrjob.job import MRJob
import numpy as np# M为矩阵A的行数,N为矩阵B的列数
M, N = 3, 3class MatrixMultiplication(MRJob):def mapper(self, _, line):# 根据数据的格式,解析输入并区分矩阵A和矩阵B的元素# 假设输入格式为 (i, j, matrix_name, value)i, j, matrix_name, value = line.split()if matrix_name == 'A':for k in range(1, N+1):yield (int(i), k), (matrix_name, int(j), int(value))else:for k in range(1, M+1):yield (k, int(j)), (matrix_name, int(i), int(value))def reducer(self, key, values):A_set, B_set = [], []for v in values:if v[0] == 'A':A_set.append(v)else:B_set.append(v)res = 0for v1 in A_set:for v2 in B_set:if v2[1] == v1[1]:res += v1[2]*v2[2]breakyield key, resif __name__ == '__main__':MatrixMultiplication.run()print("np:", np.matmul(np.array([[2, 1, 3, 4], [10, -8, 7, 2], [9, 1, 6, -2]]), np.array([[3, 2, -8], [1, 5, 2], [4, -7, 3], [4, 1, -7]])))运行命令
python matmul.py -r inline matrix.txt
相关文章:
)
MapReduce编程——矩阵乘法(Python版本)
数据格式 对于矩阵元素 A i j A_{ij} Aij,将其处理为 < i , j , M a t r i x N a m e , v a l u e > <i,j,MatrixName,value> <i,j,MatrixName,value>的四元组格式,例如矩阵[[2, 1, 3, 4], [10, -8, 7, 2], [9, 1, 6, -2]]可被转化…...
nature日报:为什么印度德里现在的空气污染如此严重?
为什么印度德里现在的空气污染如此严重? 后季风季节为印度大城市的空气污染积累创造了理想的条件。 本文整理扩展自2023年11月10日nature杂志的NEWS EXPLAINER——Why is Delhi’s air pollution so bad right now? (nature.com) Highlights 季风期间࿰…...
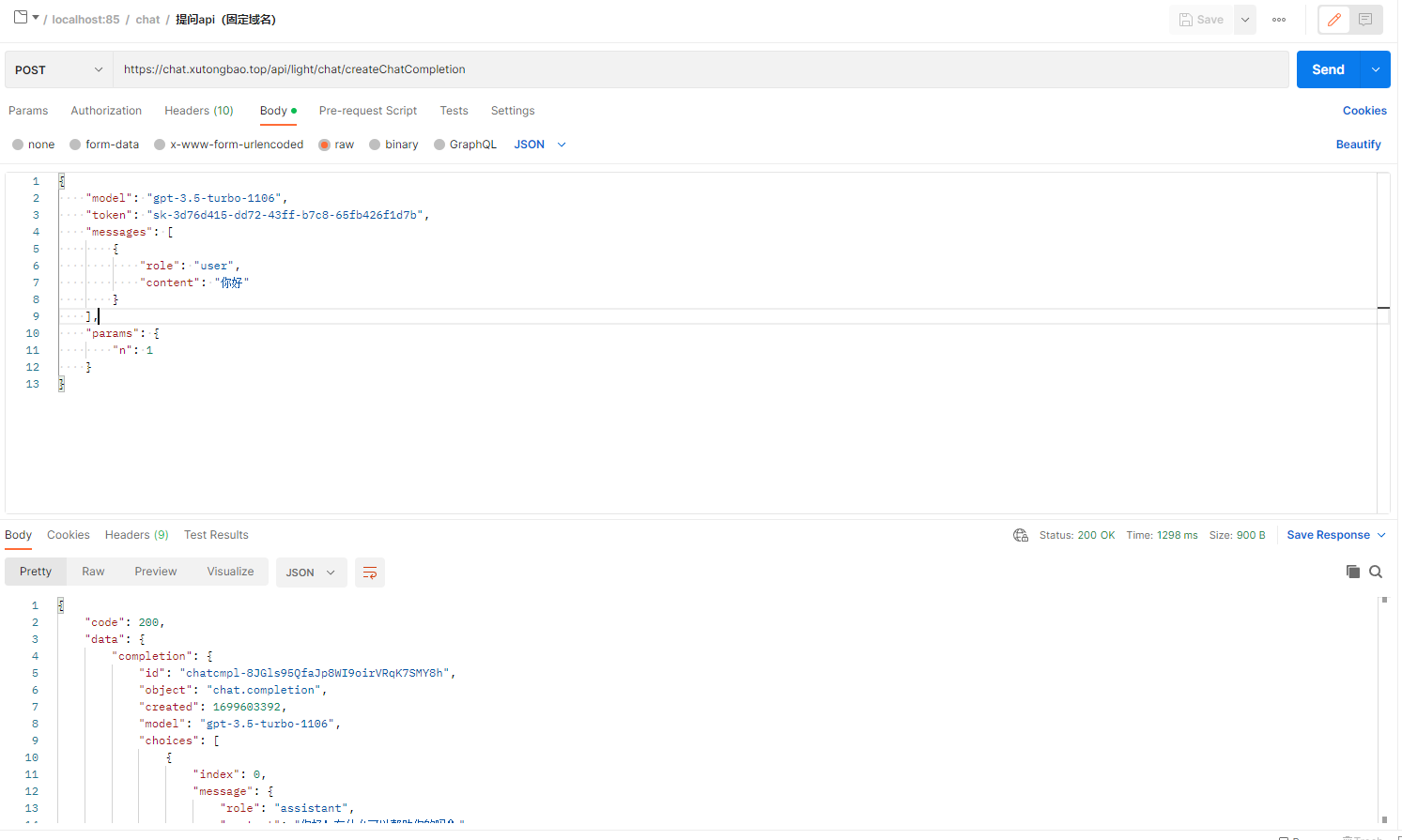
ChatGPT、GPT-4 Turbo接口调用
接口地址 https://chat.xutongbao.top/api/light/chat/createChatCompletion 请求方式 post 请求参数 model可选值: “gpt-3.5-turbo-1106”、 “gpt-3.5-turbo-16k” 、 “gpt-4”、“gpt-4-1106-preview”。 默认值为: “gpt-3.5-turbo-1106” to…...

IDEA中常用的调试快捷键
启动调试 对于Maven项目:Shift F9 对于普通项目:Shift F10 进入调试模式 Shift F9 逐行执行 逐行跳过:F8 逐行步入:F7 逐行步出:Shift F8 继续执行 F9 停止调试 Ctrl F2 设置断点 在代码行号左侧双击&#x…...

需要设计易清洗的口琴
我发现口琴很容易被异物影响。然后就需要清洗。正好手头有一个合适的螺丝刀,还比较方便。 反之一想,应该设计一种口琴,可以方便的拆开,用水清洗。晾干后就能组装。设计上当然会面临一些问题,比如音簧容易变音等。这个可…...
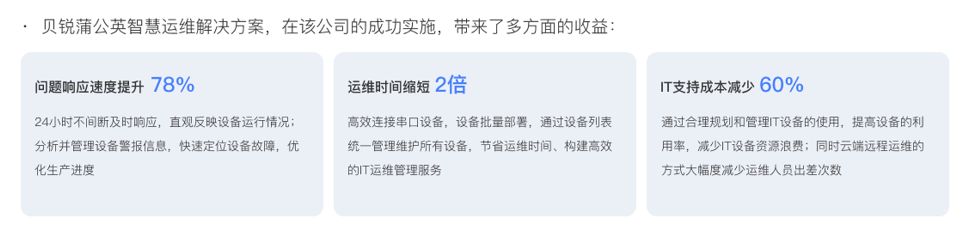
贝锐蒲公英智慧运维方案:实现远程网络监控、管理、维护工业设备
为了提升运维效率,能够及时发现和响应设备的故障、异常和潜在问题。 越来越多的企业都在搭建“集中式”的远程智慧运维体系,以提高运维效率和降低成本。 但是,受限于网络,将不同地域的资源和信息进行整合,实现统一管理…...

Intel oneAPI笔记(4)--jupyter官方文档(Unified Shared Memory)学习笔记
前言 本文是对jupyterlab中oneAPI_Essentials/03_Unified_Shared_Memory文档的学习记录,主要包含对统一共享内存的讲解 USM概述 USM (Unified Shared Memory)是SYCL中基于指针的内存管理。对于使用malloc或new来分配数据的C和C程序员来说应该很熟悉。当将现有的C…...

dRep-基因组质控、去冗余及物种界定
文章目录 Install依赖关系 常用命令常见问题pplacer线程超过30报错当比较基因组很多(>4096)有了Bdv.csv文件后无需输入基因组list 超多基因组为什么需要界定种?dRep重要概念次级ANI的选择Minimum alignment coverage3. 选择有代表性的基因…...

截图贴图软件推荐 - 附下载链接 | Snipaste | Steuna
截图贴图软件推荐 - 附下载链接 | Snipaste | Steuna 前言下载链接Snipaste(推荐)Steuna 前言 Win系统下截图软件多种多样,但贴图软件少之又少,本文介绍2个带有贴图功能的截图软件,分别是Snipaste和Steuna。可将截图固…...
python调用chrome实现网页自动操作
一. 内容简介 python调用chrome实现网页自动操作。 二. 软件环境 2.1vsCode 2.2Anaconda version: conda 22.9.0 2.3代码 链接: 三.主要流程 3.1 下载驱动和插件 调用谷歌浏览器,需要下载浏览器驱动(https://registry.npmmirror.co…...
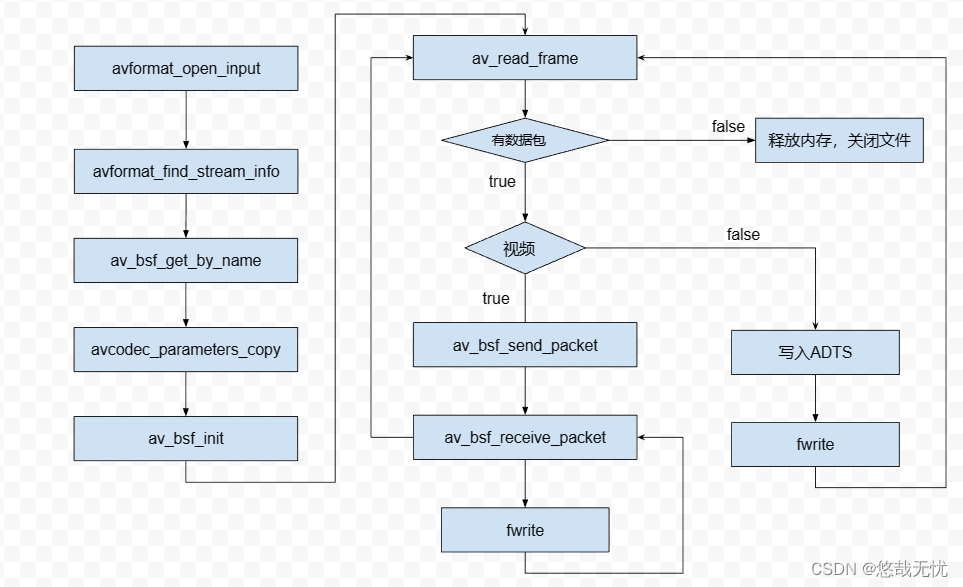
FFMPEG库实现mp4/flv文件(H264+AAC)的封装与分离
ffmepeg 4.4(亲测可用) 一、使用FFMPEG库封装264视频和acc音频数据到 mp4/flv 文件中 封装流程 1.使用avformat_open_input分别打开视频和音频文件,初始化其AVFormatContext,使用avformat_find_stream_info获取编码器基本信息 2.使…...
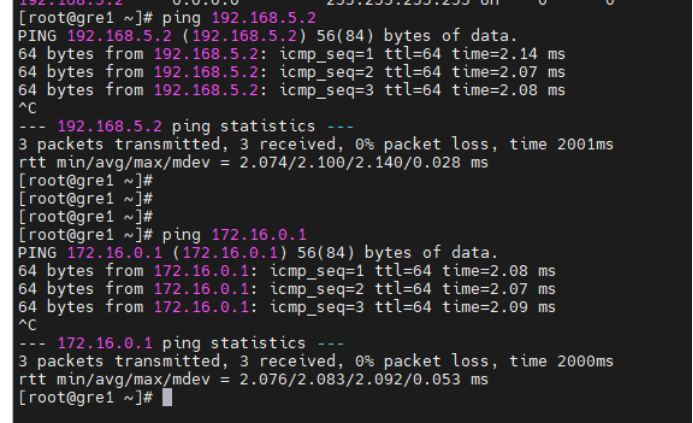
《红蓝攻防对抗实战》九.内网穿透之利用GRE协议进行隧道穿透
前文推荐: 《红蓝攻防对抗实战》一. 隧道穿透技术详解 《红蓝攻防对抗实战》二.内网探测协议出网之TCP/UDP协议探测出网 《红蓝攻防对抗实战》三.内网探测协议出网之HTTP/HTTPS协议探测出网 《红蓝攻防对抗实战》四.内网探测协议出网之ICMP协议探测出网 《红蓝…...

大数据毕业设计选题推荐-智慧消防大数据平台-Hadoop-Spark-Hive
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

LeetCode 面试题 16.20. T9键盘
文章目录 一、题目二、C# 题解 一、题目 在老式手机上,用户通过数字键盘输入,手机将提供与这些数字相匹配的单词列表。每个数字映射到0至4个字母。给定一个数字序列,实现一个算法来返回匹配单词的列表。你会得到一张含有有效单词的列表。映射…...

systemctl enable docker.service报错“Failed to execute operation: Bad message“
将docker加入到开机自启,报错: 解决: 重新粘贴复制: [Unit] DescriptionDocker Application Container Engine Documentationhttps://docs.docker.com Afternetwork-online.target firewalld.service Wantsnetwork-online.target…...
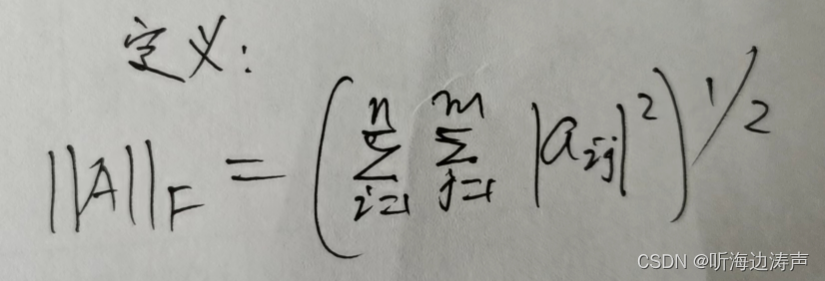
向量的范数、矩阵的范数
向量的范数 p-范数 常用的0-范数、1-范数、2-范数、无穷-范数其实都是p-范数的特殊情形。 0-范数 当p0时,表示0-范数。它比较特殊,本质是一种计数,表示向量中非0元素的个数。 1-范数(也称L1范数) 当p1时ÿ…...
C# OpenCvSharp 玉米粒计数
效果 项目 代码 using OpenCvSharp; using System; using System.Drawing; using System.Text; using System.Windows.Forms;namespace OpenCvSharp_Demo {public partial class frmMain : Form{public frmMain(){InitializeComponent();}string fileFilter "*.*|*.bmp;…...
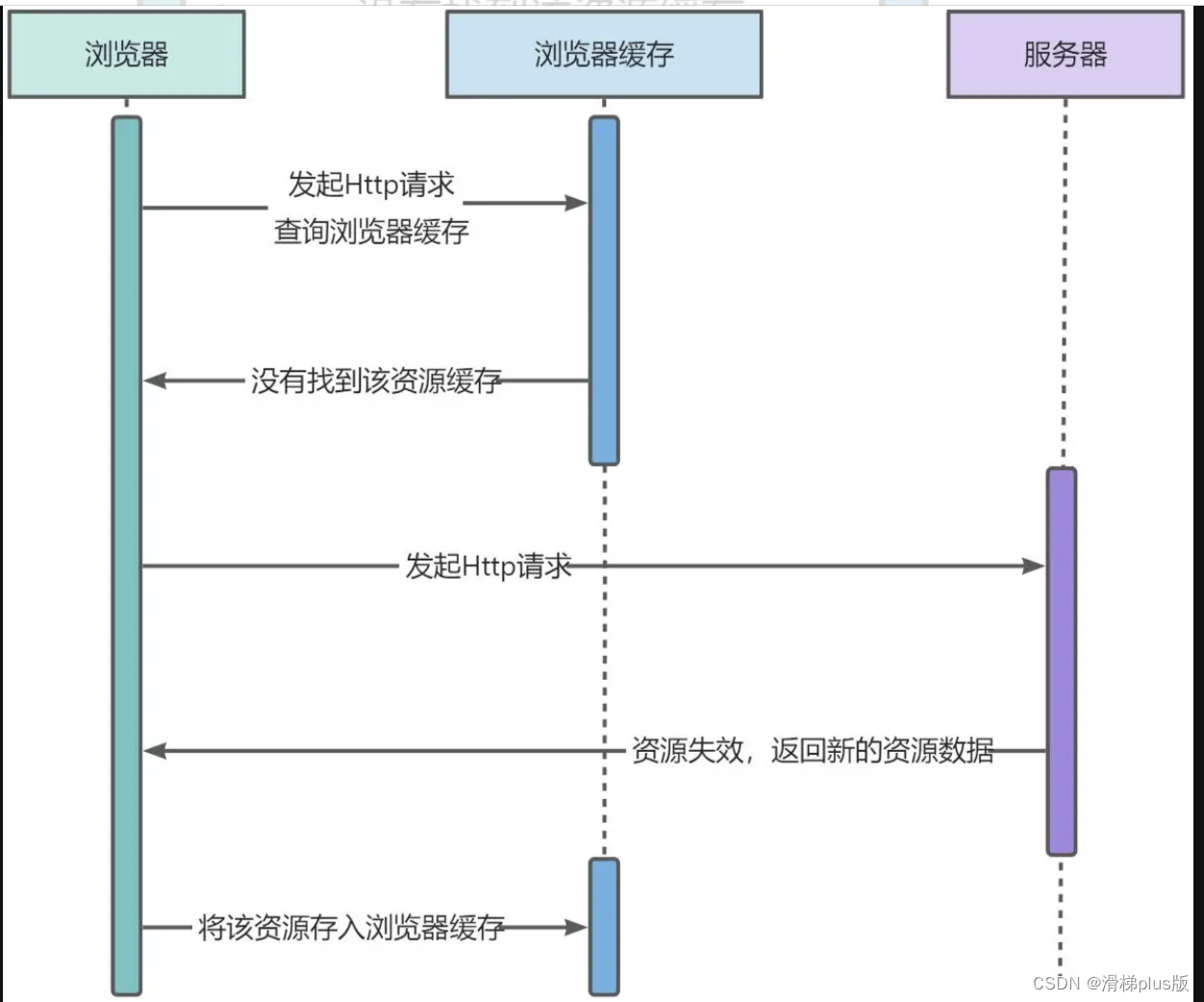
前端缓存机制——强缓存、弱缓存、启发式缓存
强缓存和弱缓存的主要区别是主要区别在于缓存头携带的信息不同。 强缓存: 浏览器发起请求,查询浏览器的本地缓存,如果找到资源,则直接在浏览器中使用该资源。若是未找到,或者资源已过期,则浏览器缓存返回未…...

对称密钥加密与非对称密钥加密:原理与应用
在信息安全领域,对称密钥加密和非对称密钥加密是两种重要的加密方法,它们各有特点,适用于不同的场景。本文将详细介绍这两种加密方法的原理,并通过实例说明其应用,同时阐述在报文传输过程中,何时使用对称密…...

商品小类管理实现B
<?xml version="1.0" encoding="UTF-8" ?> <!DOCTYPE mapperPUBLIC "-//mybatis.org//DTD Mapper 3.0//EN""http://mybatis.org/dtd/mybatis-3-mapper.dtd"> <mapper namespace="com.java1234.mapper.SmallType…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
