代码随想录算法训练营day44 | 动态规划之完全背包 518. 零钱兑换 II 377. 组合总和 Ⅳ
day44
- 完全背包基础知识
- 问题描述
- 举个栗子
- 518. 零钱兑换 II
- 1.确定dp数组以及下标的含义
- 2.确定递推公式
- 3.dp数组如何初始化
- 4.确定遍历顺序
- 5.举例推导dp数组
- 377. 组合总和 Ⅳ
- 1.确定dp数组以及下标的含义
- 2.确定递推公式
- 3.dp数组如何初始化
- 4.确定遍历顺序
- 5.举例来推导dp数组
完全背包基础知识
问题描述
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
举个栗子
背包最大重量为4。
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
完全背包的物品是可以添加多次的,所以要从小到大去遍历
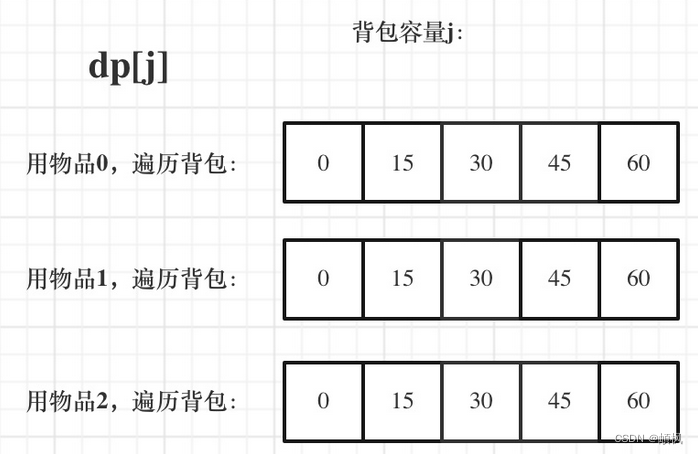
// 先遍历物品,在遍历背包
void test_CompletePack() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagWeight = 4;vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}
int main() {test_CompletePack();
}518. 零钱兑换 II
题目链接
解题思路: 纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物品组合个数!是一个组合问题。组合不强调元素之间的顺序,排列强调元素之间的顺序。
动规五步曲:
1.确定dp数组以及下标的含义
dp[j]:凑成总金额j的货币组合数为dp[j]
2.确定递推公式
dp[j] 就是所有的dp[j - coins[i]](考虑coins[i]的情况)相加。
所以递推公式:dp[j] += dp[j - coins[i]];
这个递推公式01背包题目的时候在这篇494. 目标和
(opens new window)中出现过,求装满背包有几种方法,公式都是:dp[j] += dp[j - nums[i]];
3.dp数组如何初始化
首先dp[0]一定要为1,dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话,后面所有推导出来的值都是0了。
dp[0]=1还说明了一种情况:如果正好选了coins[i]后,也就是j-coins[i] == 0的情况表示这个硬币刚好能选,此时dp[0]为1表示只选coins[i]存在这样的一种选法。
4.确定遍历顺序
本题中我们是外层for循环遍历物品(钱币),内层for遍历背包(金钱总额),还是外层for遍历背包(金钱总额),内层for循环遍历物品(钱币)呢?在上面的讲解中完全背包的两个for循环的先后顺序都是可以的。
但本题就不行了!
因为纯完全背包求得装满背包的最大价值是多少,和凑成总和的元素有没有顺序没关系,即:有顺序也行,没有顺序也行!
而本题要求凑成总和的组合数,元素之间明确要求没有顺序。
所以纯完全背包是能凑成总和就行,不用管怎么凑的。
本题是求凑出来的方案个数,且每个方案个数是为组合数。
那么本题,两个for循环的先后顺序可就有说法了。
我们先来看 外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)的情况。
代码如下:
for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量dp[j] += dp[j - coins[i]];}
}假设:coins[0] = 1,coins[1] = 5。
那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。
所以这种遍历顺序中dp[j]里计算的是组合数!
如果把两个for交换顺序,代码如下:
for (int j = 0; j <= amount; j++) { // 遍历背包容量for (int i = 0; i < coins.size(); i++) { // 遍历物品if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];}
}背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。
此时dp[j]里算出来的就是排列数!
5.举例推导dp数组
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:
 最后红色框
最后红色框dp[amount]为最终结果。
C++代码如下:
class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount + 1, 0);dp[0] = 1;for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包dp[j] += dp[j - coins[i]];}}return dp[amount];}
};377. 组合总和 Ⅳ
题目链接
解题思路:本题题目描述说是求组合,但又说是可以元素相同顺序不同的组合算两个组合,其实就是求排列。
动规五部曲分析如下:
1.确定dp数组以及下标的含义
dp[i]: 凑成目标正整数为i的排列个数为dp[i]
2.确定递推公式
dp[i](考虑nums[j])可以由 dp[i - nums[j]](不考虑nums[j]) 推导出来。
因为只要得到nums[j],排列个数dp[i - nums[j]],就是dp[i]的一部分。
求装满背包有几种方法,递推公式一般都是dp[i] += dp[i - nums[j]];
本题也一样。
3.dp数组如何初始化
因为递推公式dp[i] += dp[i - nums[j]]的缘故,dp[0]要初始化为1,这样递归其他dp[i]的时候才会有数值基础。
至于dp[0] = 1 有没有意义呢?
其实没有意义,所以我也不去强行解释它的意义了,因为题目中也说了:给定目标值是正整数! 所以dp[0] = 1是没有意义的,仅仅是为了推导递推公式。
至于非0下标的dp[i]应该初始为多少呢?
初始化为0,这样才不会影响dp[i]累加所有的dp[i - nums[j]]。
4.确定遍历顺序
个数可以不限使用,说明这是一个完全背包。
得到的集合是排列,说明需要考虑元素之间的顺序。
本题要求的是排列,那么这个for循环嵌套的顺序可以有说法了。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
如果把遍历nums(物品)放在外循环,遍历target的作为内循环的话,
举个栗子:
计算dp[4]的时候,结果集只有 {1,3} 这样的集合,不会有{3,1}这样的集合,因为nums遍历放在外层,3只能出现在1后面!
所以本题遍历顺序最终遍历顺序:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前到后遍历。
5.举例来推导dp数组
我们再来用示例中的例子推导一下:
输入:nums =[1,2,3] , target = 4
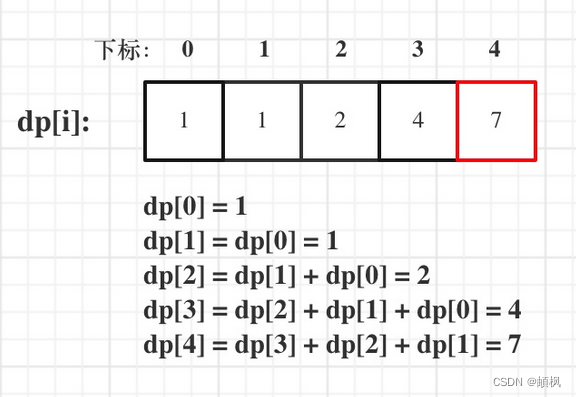
C++代码如下:
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target + 1, 0);dp[0] = 1;for (int i = 0; i <= target; i++) { // 遍历背包for (int j = 0; j < nums.size(); j++) { // 遍历物品if (i - nums[j] >= 0 && dp[i] < INT_MAX - dp[i - nums[j]]) {dp[i] += dp[i - nums[j]];}}}return dp[target];}
};相关文章:

代码随想录算法训练营day44 | 动态规划之完全背包 518. 零钱兑换 II 377. 组合总和 Ⅳ
day44完全背包基础知识问题描述举个栗子518. 零钱兑换 II1.确定dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组377. 组合总和 Ⅳ1.确定dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例来推导dp数组完全背包基…...
IntelliJ IDEA 实用插件推荐(包含使用教程)
IntelliJ IDEA 实用插件推荐 背景:电脑重装了,重新下载了最新版的IntelliJ IDEA,感觉默认模式有点枯燥,于是决定从网上下载一些实用美观的插件优化自己以后吃饭的工具,现在推荐的都是目前还能用的(亲身实践…...

WideDeep模型
google提出的Wide&deep模型,将线性模型与DNN很好的结合起来,在提高模型泛化能力的同时,兼顾模型的记忆性。wide&deep这种将线性模型与DNN的并行连接模式,后来称为推荐领域的经典模式,奠定了后面深度学习模型的…...
nacos集群模式+keepalived搭建高可用服务
实际工作中如果nacos这样的核心服务停掉了或者整个服务器宕机了,那整个系统也就gg了,所以像这样的核心服务我们必须要搞个3个或者3个以上的nacos集群部署,实现高可用; 部署高可用版本之前,首先你要会部署单机版的naco…...

吉利「银河」负重突围
吉利控股集团最新公布的数据显示,2022年,吉利控股集团汽车总销量超230万辆,同比增长4.3%。其中,新能源汽车销量超64万辆,同比增长100.3%。 在中国本土市场,2022年吉利集团旗下品牌乘用车总交付量为135.84万…...

QT之图形视图框架概述——Graphics View Framework
QT之图形视图框架概述——Graphics View Framework1. 概述2. 核心类3. 事件传递4. Graphics View 坐标系统5. 参考1. 概述 Graphics View Framework是子Qt 4.2引入的,用来取代之前版本中的QCanvas。Graphics View Framework提拱了用于大量2D图形项的管理和交互的能…...
:数仓报表场景(上) 从分析函数效率一定快吗聊一聊结果集分页和隔行抽样实现方式)
【SQL开发实战技巧】系列(二十二):数仓报表场景(上) 从分析函数效率一定快吗聊一聊结果集分页和隔行抽样实现方式
系列文章目录 【SQL开发实战技巧】系列(一):关于SQL不得不说的那些事 【SQL开发实战技巧】系列(二):简单单表查询 【SQL开发实战技巧】系列(三):SQL排序的那些事 【SQL开发实战技巧…...

小米无线AR眼镜探索版细节汇总
在MWC 2023期间,小米正式发布了一款无线AR眼镜,虽然还没看过实机,但XDA提前上手体验,我们从中进行总结。首先我要说的是,小米这款眼镜和高通无线AR眼镜参考设计高度重叠,产品卖点几乎一致,只是增…...

Web3中文|Litra:简洁而优美的NFT流动性协议,能给NFT市场带来什么?
2021年,NFT元年2021年,无疑是 NFT 的“元年”。这一年推特创始人的首条推特被拍出250万美元,加密艺术家Beeple的数字作品“First 5000 Days”在佳士得以6900万美元价格成交,无聊猿最高上涨了1800倍。2021年11月,在Goog…...

SSL证书对虚拟主机的用处有哪些?
虚拟主机是指在同一台服务器上,通过不同的域名或IP地址为多个网站提供服务的一种网络主机。而SSL证书则是一种数字证书,它用于加密网站与用户之间的通信,确保数据传输的安全性和完整性。在虚拟主机上,SSL证书有以下几个用处&#…...
SpringCloud之MQ笔记分享
MQ异步通信 初始MQ 同步通信 优点:时效性较强,可以以及得到结果 Feign就属于同步方式–问题: 耦合问题性能下降(中间的等待时间)资源浪费级联失败 异步通信 优点 耦合度低性能提升,吞吐量高故障隔离…...
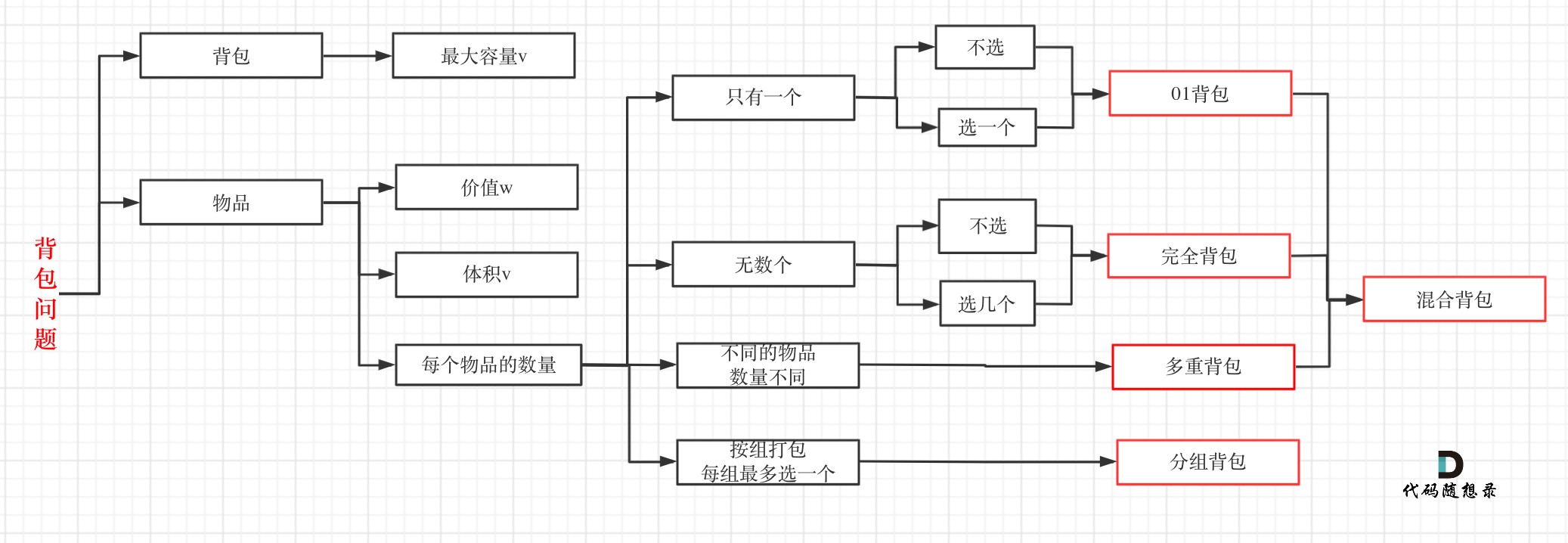
动态规划背包问题
背包问题的分类 拿到背包问题,最重要的是会归类到哪一种背包问题中,常见的考题里主要是01背包和完全背包,leetcode上连多重背包的题目都没有。实际完全背包问题就是01背包的一种。 对一和零这道题,很多人容易把m看成一个背包,n看成另一个背包,从而当做多重背包。然而这…...

OpenCV4.x图像处理实例-张嘴和闭嘴检测
张嘴和闭嘴检测 在活体验证中,张嘴和闭嘴检测也是一个重要的环节。本文将介绍如何通过检测人脸上唇和下唇的关键点,并计算上唇和下唇的关键点的距离来检测当前人脸状态是否处于张嘴或闭嘴。 张嘴和闭嘴检测主要步骤如下: 第一步,安装依赖库 示例中使用到OpenCV和MediaP…...

软考高级系统分析师系列论文之十二:论实时控制系统与企业信息系统集成在工业控制的常规应用
软考高级系统分析师系列论文之十二:论实时控制系统与企业信息系统集成在工业控制的常规应用 一、摘要二、正文三、总结一、摘要 本文通过“工控组态软件”项目的开发,着重讨论实时系统与信息系统的集成。近年来,国内外的组态软件取得了很大的发展,已广泛应用于企业生产。组…...
货物摆放问题)
蓝桥杯入门即劝退(二十三)货物摆放问题
欢迎关注点赞评论,共同学习,共同进步! ------持续更新蓝桥杯入门系列算法实例-------- 如果你也喜欢Java和算法,欢迎订阅专栏共同学习交流! 你的点赞、关注、评论、是我创作的动力! -------希望我的文章…...
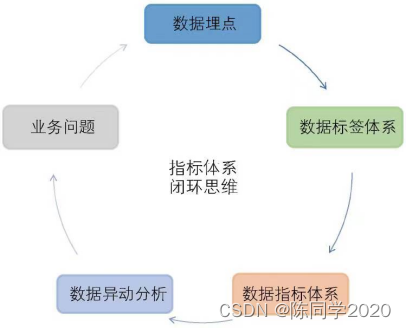
经验之谈——指标异常了怎么办?
本文参考了数据万花筒的文章,结合我自己工作经验。希望给大家一些帮助。 指标异常排查,是数据分析师的工作重点之一,是各行各业数据分析师都绕不开的话题。 本文试图回答: 1、指标波动的影响因素有哪些? 2、如何快速…...

影视领域解说电影怎样做才会更加出彩?
还有没有想要做影视解说的新手朋友~给大家分享一下影视解说快速上手的软件工具! 一、解说文案 文案是影视解说中最重要的步骤,如果你无法保证文案足够优秀,那么请务必让所有语句通顺,整体通篇下来让人知道你是在讲一个完整的故事…...

【Spring6】| Spring对IoC的实现(核心重点)
目录 一:Spring对IoC的实现 1. IoC 控制反转 2. 依赖注入 2.1 set注入 2.2 构造注入 3. set注入专题 3.1 注入外部Bean 3.2 注入内部Bean 3.3 注入简单类型 3.4 级联属性赋值(了解) 3.5 注入数组 3.6 注入List集合和Set集合 3.7…...
部门来了个测试工程师,听说是00后,实在是太卷了.....
都说00后躺平了,但是有一说一,该卷的还是卷。 这不,前段时间我们部门来了个00后,工作没两年,跳槽到我们公司起薪18K,都快接近我了。后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了。…...

冲冲冲,力扣javascript刷题——数组总结
力扣javascript刷题——数组总结冲冲冲,力扣刷题——数组总结1.二分查找力扣704题:二分查找35.搜索插入位置34.在排序数组中查找元素的第一个和最后一个位置69.x 的平方根367. 有效的完全平方数2.双指针法27. 移除元素26. 删除有序数组中的重复项283.移动零844. 比较…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
