畅通工程之局部最小花费问题 (C++)
目录
题目:
思路:
代码:
结果
题目:

思路:
详细思路都在代码注释里 。
代码:
#include<iostream>//无向图邻接矩阵
#include<map>
#include<algorithm>
#define mvnum 1005
using namespace std;
typedef int Vertextype;//顶点数据类型
map<Vertextype, int> mp;
typedef struct
{int data;int build;
}Arctype;//边权值类型
typedef struct
{Vertextype vexs[mvnum];//顶点表Arctype arcs[mvnum][mvnum];//邻接矩阵int vexnum, arcnum;//当前图的点数和边数
}AMGraph;
typedef struct
{Vertextype head;//始点Vertextype tail;//终点int w;//权值int build;
}edge;//边
int v[mvnum];//辅助数组,记录连通分支
edge e[50000];
bool Creategraph(AMGraph& G)
{cin >> G.vexnum;//输入总顶点数G.arcnum = G.vexnum * (G.vexnum - 1) / 2;//总边数for (int i = 1; i <= G.vexnum; i++)//初始化邻接矩阵for (int j = 1; j <= G.vexnum; j++)G.arcs[i][j].data = 0;for (int k = 0; k < G.arcnum; k++)//构造邻接矩阵{Vertextype v1, v2;int w, d;int t = 0;cin >> v1 >> v2 >> w >> d;//输入一条边的顶点及边的权值int i = v1;int j = v2;//确定v1和v2在G中的位置if (d == 1)//已经建造G.arcs[i][j].data = 0;//即不用再花钱elseG.arcs[i][j].data = w;//边<v1,v2>的权值置为wG.arcs[i][j].build = d;//是否建造G.arcs[j][i] = G.arcs[i][j];//无向图是对称图e[k].head = i, e[k].tail = j, e[k].w = G.arcs[i][j].data, e[k].build = d;}return 1;
}
/*void Print(AMGraph G)
{cout << "邻接矩阵:" << endl;for (int i = 1; i <= G.vexnum; i++){for (int j = 1; j <= G.vexnum; j++)cout << G.arcs[i][j].data << " ";cout << endl;}
}*/
bool cmp(edge a, edge b)
{if (a.w == b.w)return a.build > b.build;return a.w < b.w;
}
int Klsk(AMGraph& G)
{int sum = 0;//cout << "边:" << endl;sort(e, e + G.arcnum, cmp);for (int i = 1; i <= G.vexnum; i++)v[i] = i;//自成连通分量for (int i = 0; i < G.arcnum; i++){int v1 = e[i].head;//取其位置int v2 = e[i].tail;//取其位置int vs1 = v[v1];//取其连通分量int vs2 = v[v2];//取其连通分量if (vs1 != vs2)//不为同一连通分量且建造通路{sum += e[i].w;//cout << e[i].head << " " << e[i].tail << " " << e[i].w << endl;for (int j = 1; j <= G.vexnum; j++)if (v[j] == vs2)//更新连通分量v[j] = vs1;}}return sum;
}
int main()
{AMGraph G;Creategraph(G);//Print(G);int ans = Klsk(G);cout << ans << endl;
}
结果:

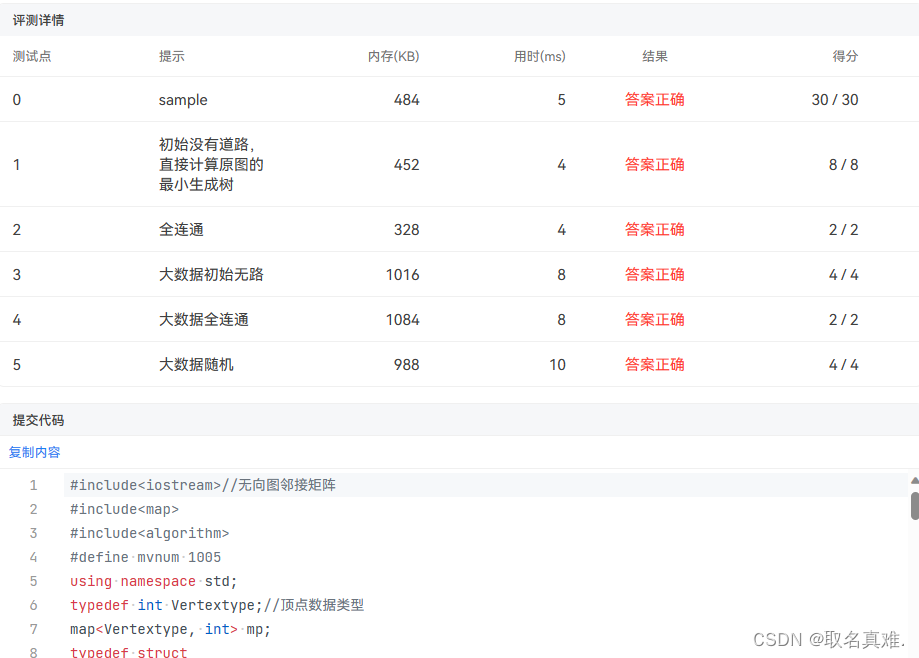
相关文章:

畅通工程之局部最小花费问题 (C++)
目录 题目: 思路: 代码: 结果 题目: 思路: 详细思路都在代码注释里 。 代码: #include<iostream>//无向图邻接矩阵 #include<map> #include<algorithm> #define mvnum 1005 using …...

Sql 异常 + Error
目录 1、Sql 异常 1、SQL Error 1、 Out of sort memory,consider increasing server sort buffer size 2、MySQL排序规则不同关联报错 3、MySQL ....LIMIT 15 4、MySQL:Data truncation: Invalid JSON text 5、MySQL:Duplicate entry ‘xx‘ for key ‘xxxx…...

基于UNI-APP实现适配器并保证适配器和实现的调用一致
概述 前端功能的实现是基于不同的环境采用不同的实现方式的。一种是企业微信小程序,需要基于企业微信框架实现。一种是移动APP,需要基于uni-app的中底层实现。为了调用方便,需要将两种实现统一在一种适配器中,调用者只需要指定环…...
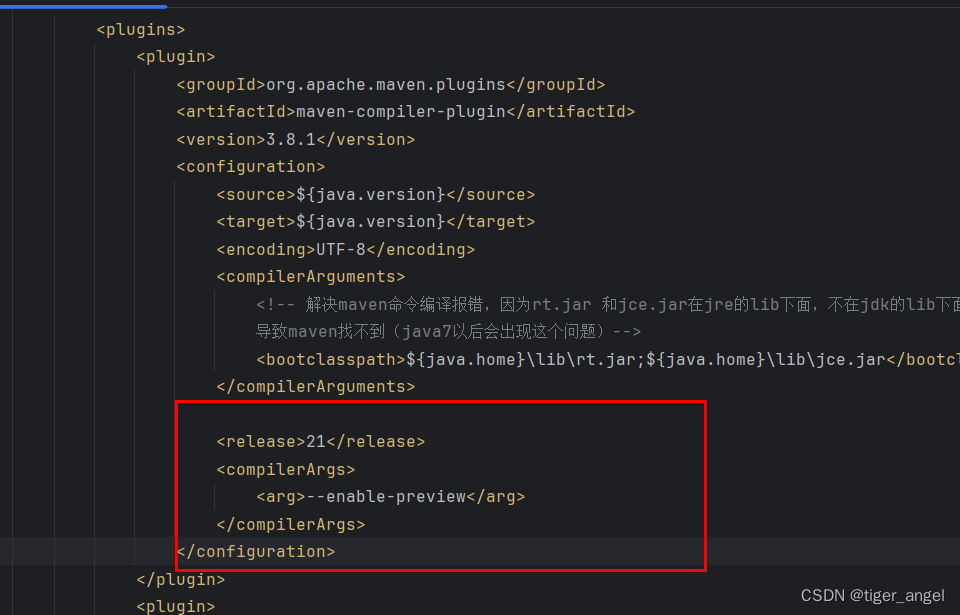
使用jdk21预览版 --enable-preview
异常 [ERROR] Failed to execute goal org.apache.maven.plugins:maven-compiler-plugin:3.10.1:compile (default-compile) on project sb3: Compilation failure [ERROR] --enable-preview 一起使用时无效 [ERROR] (仅发行版 21 支持预览语言功能) 解决…...

js中的跳转都有哪些格式
location.href "URL" :用于在当前窗口中加载其他页面。 例如:location.href "https://www.google.com" location.replace("URL"):用于在当前窗口中加载其他页面,但不保留原页面的历史记录&#…...

无重复字符的最长子串
题目 添加链接描述 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。示例 1:输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。 示例 2:输入: s "bbbbb" 输出…...
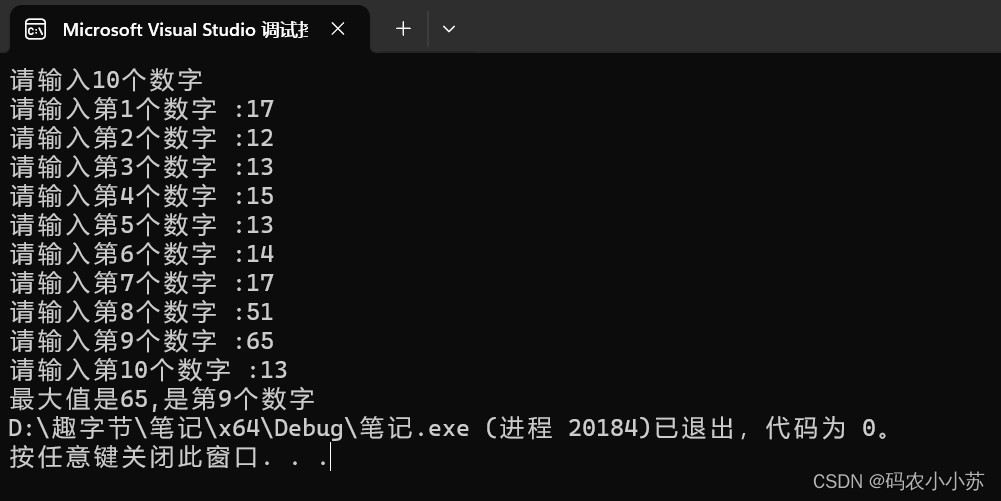
C语言--输入10个数字,要求输出其中值最大的元素和该数字是第几个数
今天小编带大家了解一下什么是“打擂台”算法。 一.思路分析 可以定义一个数组arr,长度为10,用来存放10个数字,设计一个函数Max,用来求两个数中的较大值, 定义一个临时变量tmparr[0],保存临时最大的值,下标…...

如何做好功能测试,提升测试质量和效率?
要做好功能测试并提升测试质量和效率,可以考虑以下几个方面: 1. 明确测试目标和需求 在开始功能测试之前,首先要明确测试的目标和需求,包括测试的范围、重点、预期结果等。这有助于为测试工作提供清晰的方向和指导。 2. 制定详细…...
高德地图添加信息弹窗,信息弹窗是单独的组件
//弹窗组件 <template><el-card class"box-card" ref"boxCard" v-if"showCard"><div slot"header" class"clearfix"><div class"title">{{ model.pointName }}</div><div class…...

Apache Arrow优点
优点 采用连续的内存布局,在单机计算的时候,对操作系统友好,增加了缓存命中率以及读取数据的效率采用列式存储,在单机计算的时候,可以利用SMID向量化处理,并且增加了查询效率(一般查询的时候只…...
【Linux权限:系统中的数字锁与安全之门】
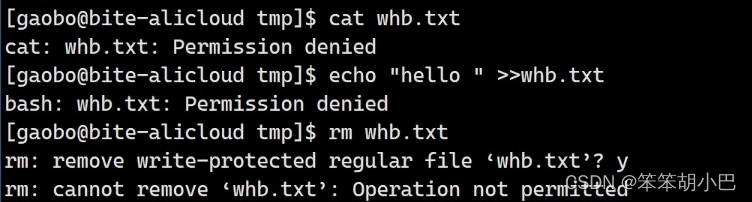
1.Linux下的用户 Linux下有两种用户:超级用户(root)、普通用户。 超级用户:可以再linux系统下做任何事情,不受限制普通用户:在linux下做有限的事情。超级用户的命令提示符是“#”,普通用户的命令…...
笔记本电脑的麦克风没有声音
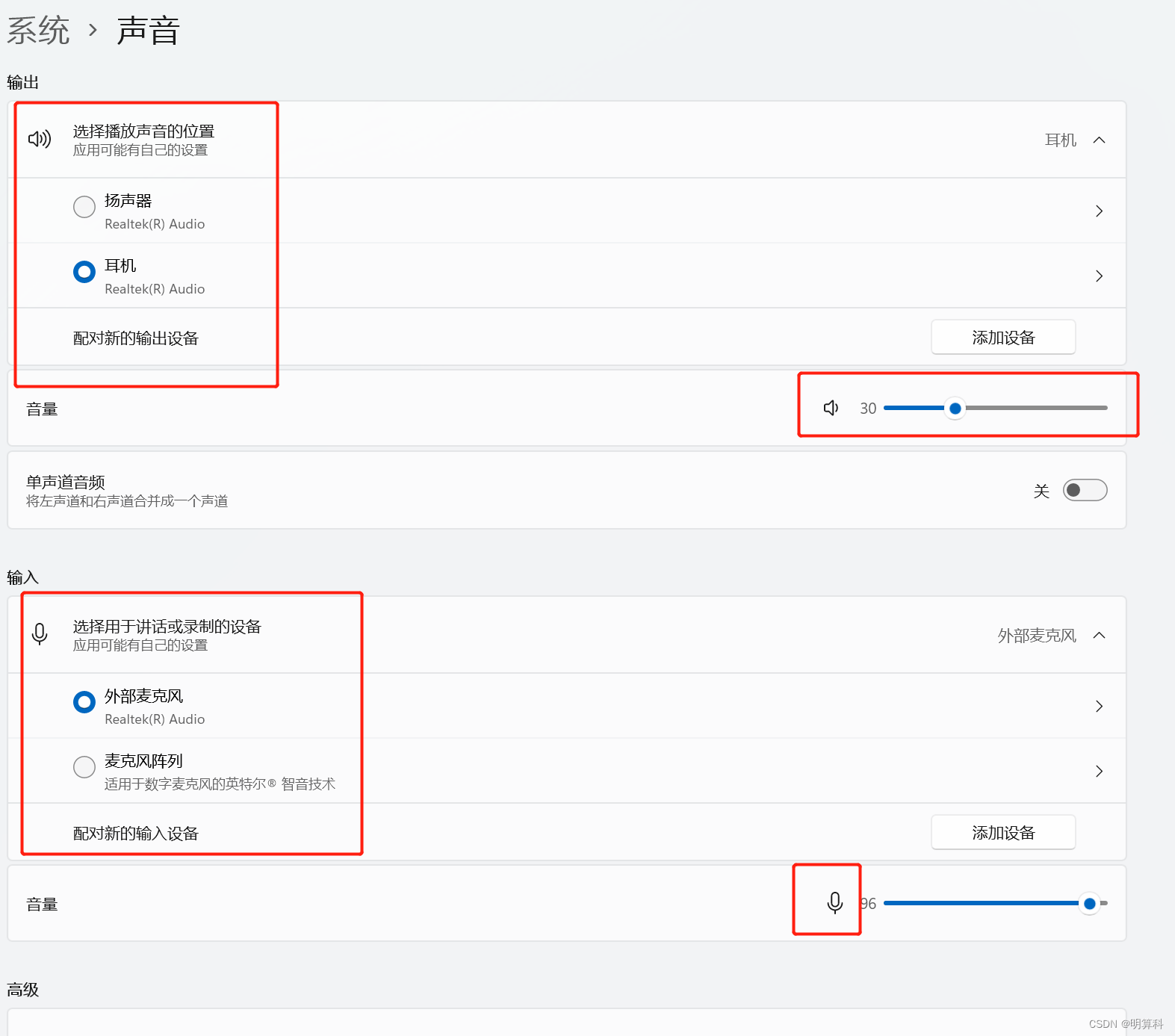
笔记本电脑的麦克风没有声音是一个常见的问题,可能是由于以下几个原因导致的: 第一,麦克风没有启用或者被禁用了。在Windows系统中,右键单击任务栏上的音量图标,选择“录音设备”,在弹出窗口中找到麦克风&a…...

20道简单的投资数学逻辑
20道简单的投资数学逻辑 (非常好,强烈推荐,其中第3、第11的案例太经典了,是我反复给金融研究生讲授分析的案例) 1、关于收益率 假如你有100万,收益100%后资产达到200万,如果接下来亏损50%&am…...
【Spring】事务实现原理
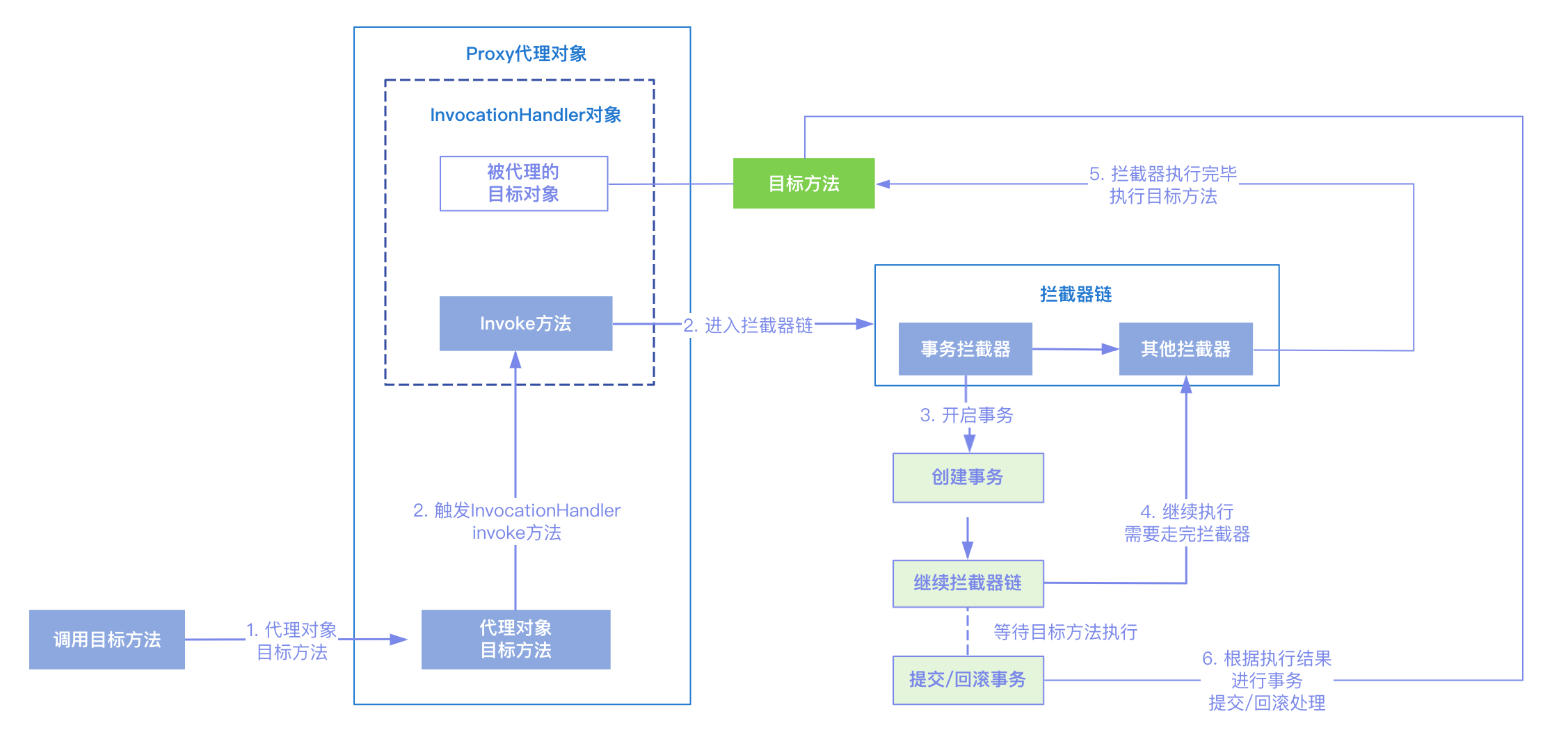
在使用事务的时候需要添加EnableTransactionManagement注解来开启事务,Spring事务底层是通过AOP来实现的,所以启用事务后,同样会向容器中注入一个代理对象创建器,AOP使用的是AnnotationAwareAspectJAutoProxyCreator,事…...
人工智能基础_机器学习024_梯度下降进阶_L1正则可视化图形---人工智能工作笔记0064
然后我们就来用代码实现一下L1正则的可视化,我们来看看 首先导入 import numpy as np 数学计算 import matplotlib.pyplot as plt 画图用的 然后我们把L1正则的公式写出来 可以看到L1的正则 其实就是w1和w2的绝对值相加对吧 然后这里我们写一个公式: f(x,y) = |x|+|y| …...

媒体聚焦丨四维图新旗下杰发科技王璐:设计决定芯片质量
编者按:新四化、软件定义汽车使汽车芯片成为了最新的半导体增长极,催生了汽车芯片的数量呈倍速增长,汽车芯片功能越来越复杂,迭代速度也越来越快。汽车芯片厂商从最初的设计开始,就要按照车规级芯片的要求对芯片进行全…...
)
动态规划基础篇(LeetCode每日一题计划)
爬楼梯 求所有爬楼梯的方案 方法一:f(x)f(x-1)f(x-2) class Solution {public int climbStairs(int n) {int p0,q0,r1;for(int i0;i<n;i){pq;qr;rpq;}return r;} } 方法二:动态规划 class Solution { public:int climbStairs(int n) {int dp[46]…...

智慧商业:探索分布式云技术为企业创造商业价值,减少成本,提升生产力的秘诀!
我们可以试想一下,如果没有云计算,商业将会是什么样子? 对于这个问题的答案,许多人会认为它可能依旧是一个以实体为主行业。 云计算和多云战略的出现为在线购物带来了革命性的变化。 然而,如今多云所固有的复杂性仍然…...

Anaconda安装gdal
安装gdal 安装gdal,真是一波三折哇。pip、conda、c编译了等等,网上各种大佬的解决方法都试了试。咱就是说,都不行,很扯淡。甚至 使用conda install gdal 都显示安装成功了,但是 from osgeo import gdal; i…...

vite基础学习笔记:14.路由跳转(二)携带query参数
说明:自学做的笔记和记录,如有错误请指正 1. 路由跳转(携带query参数) (1)第一层路由(点击卡片路由跳转至新页面-携带query参数) 知识点: query传参对应的是path和qu…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
