软文推广中如何搭建媒体矩阵
媒体矩阵简单理解就是在不同的媒体平台上,根据运营目标和需求,建立起全面系统的媒体布局,进行多平台同步运营。接下来媒介盒子就来和大家聊聊,企业在软文推广过程中为什么需要搭建媒体矩阵,又该如何搭建媒体矩阵。

一、 媒体矩阵账号优势
1. 内容多元化
每个平台的特性都不同,企业在进行软文推广时可以根据平台特性选择合适的媒体进行推广,比如短视频平台和图文平台,能够使企业以不同形式传递产品信息,多渠道触达目标用户。
2. 扩大粉丝数量
在同一平台内搭建媒体矩阵,运营不同风格的账号,可以有针对性地沉淀不同类型的粉丝群体,从而使品牌覆盖到更多人群。比如说有的用户喜欢干货知识,有的用户喜欢幽默笑话,企业就可以根据 不同用户的浏览偏好建立相应的账号,扩大粉丝数量。
3. 提升转化率
建立矩阵后,我们可以通过精细化的运营,使不同平台的产品和调性形成互补,比方说当有产品购买意向的客户在视频平台看到产品信息后,又在图文平台看到关于该产品的详细说明,就有较大概率购买产品。
二、 媒体矩阵类型
搭建媒体矩阵前,需要先确定矩阵类型,媒体矩阵共分为横向矩阵和纵向矩阵两种类型。
1. 横向矩阵
横向矩阵指企业在全媒体平台的布局,包括自有APP、网站、各类自媒体平台等,也可以称为外矩阵。
2. 纵向矩阵
纵向矩阵主要指企业在某个平台内的生态布局,是其各个产品线的纵深布局,也可以称之为内矩阵。
三、 选择合适的平台
确定媒体矩阵类型后,就需要选择合适的平台推广,不同平台有不同的类型特点,在这里盒子给大家分享常见的媒体类型。
1. 自媒体
自媒体平台具有交互性强、用户活跃度高、创作自由等属性,适合推广社交属性较强的产品或服务,企业可以在上面建立官方账号与用户积极互动,还可以与平台内博主进行合作推广,扩大用户范围。
2. 垂直媒体
垂直媒体具有专业性强的特点,适用于垂直领域的企业或个人,如汽车、金融、健康等,企业在垂直媒体发布的文案可以是干货知识、产品信息等,能够带给用户价值感,树立品牌专业形象。
3. 新闻媒体
新闻媒体具有权威性高、覆盖面广的优势,企业可以建立账号发布相关的新闻资讯,如行业趋势分析、新品发布活动、公益活动等等,这类信息能够建立企业正面形象,增强用户信赖感,同时当负面舆论来临时,企业也可以通过新闻报道进行危机公关。
四、 总结
在当今的数字营销领域,搭建媒体矩阵进行软文推广已经成为企业营销的必要手段,需要注意的是,不同的平台有不同的用户群体和偏好,因此在发布内容时,企业也需要根据不同平台的特性进行适当调整,这样不仅能扩大品牌覆盖范围,还能提高搜索引擎排名。

想要了解更多干货,欢迎关注我们~
相关文章:

软文推广中如何搭建媒体矩阵
媒体矩阵简单理解就是在不同的媒体平台上,根据运营目标和需求,建立起全面系统的媒体布局,进行多平台同步运营。接下来媒介盒子就来和大家聊聊,企业在软文推广过程中为什么需要搭建媒体矩阵,又该如何搭建媒体矩阵。 一、…...

Unity地面交互效果——5、角色足迹的制作
大家好,我是阿赵。 之前几篇文章,已经介绍了地面交互的轨迹做法。包括了法线、曲面细分还有顶点偏移。Shader方面的内容已经说完了,不过之前都是用一个球来模拟轨迹,这次来介绍一下,怎样和角色动作结合,…...

Centos8安装出错问题
科普介绍: CentOS 8 是一个基于 Linux 的操作系统,是 Red Hat Enterprise Linux (RHEL)的免费和开源版本。它提供了稳定、安全和可靠的基础设施,适用于服务器和桌面环境。CentOS 8 是 CentOS 系列中最新的版本&#x…...

计算机网络技术
深入浅出计算机网络 微课视频_哔哩哔哩_bilibili 第一章概述 1.1 信息时代的计算机网络 1. 计算机网络各类应用 2. 计算机网络带来的负面问题 3. 我国互联网发展情况 1.2 因特网概述 1. 网络、互连网(互联网)与因特网的区别与关系 如图所示࿰…...
)
当电脑桌面黑屏,而你只有一个鼠标该怎么办(重启方法的平替)
作为一个打工人 电脑是不是黑屏简直是routine了 我们都知道重启能解决一切问题 但是!! 如果你只有一个鼠标 电脑因为种种原因没法重启 该怎么办呢? 别慌 下面的方法非常灵验 1.按住ctrlShiftEsc 调出任务管理器;此项为必须…...
Leetcode2833. 距离原点最远的点
Every day a Leetcode 题目来源:2833. 距离原点最远的点 解法1:贪心 要使得到达的距离原点最远的点,就看 left 和 right 谁大,将 left 和 right 作为矢量相加,再往同方向加上 underline。 答案即为 abs(left - rig…...
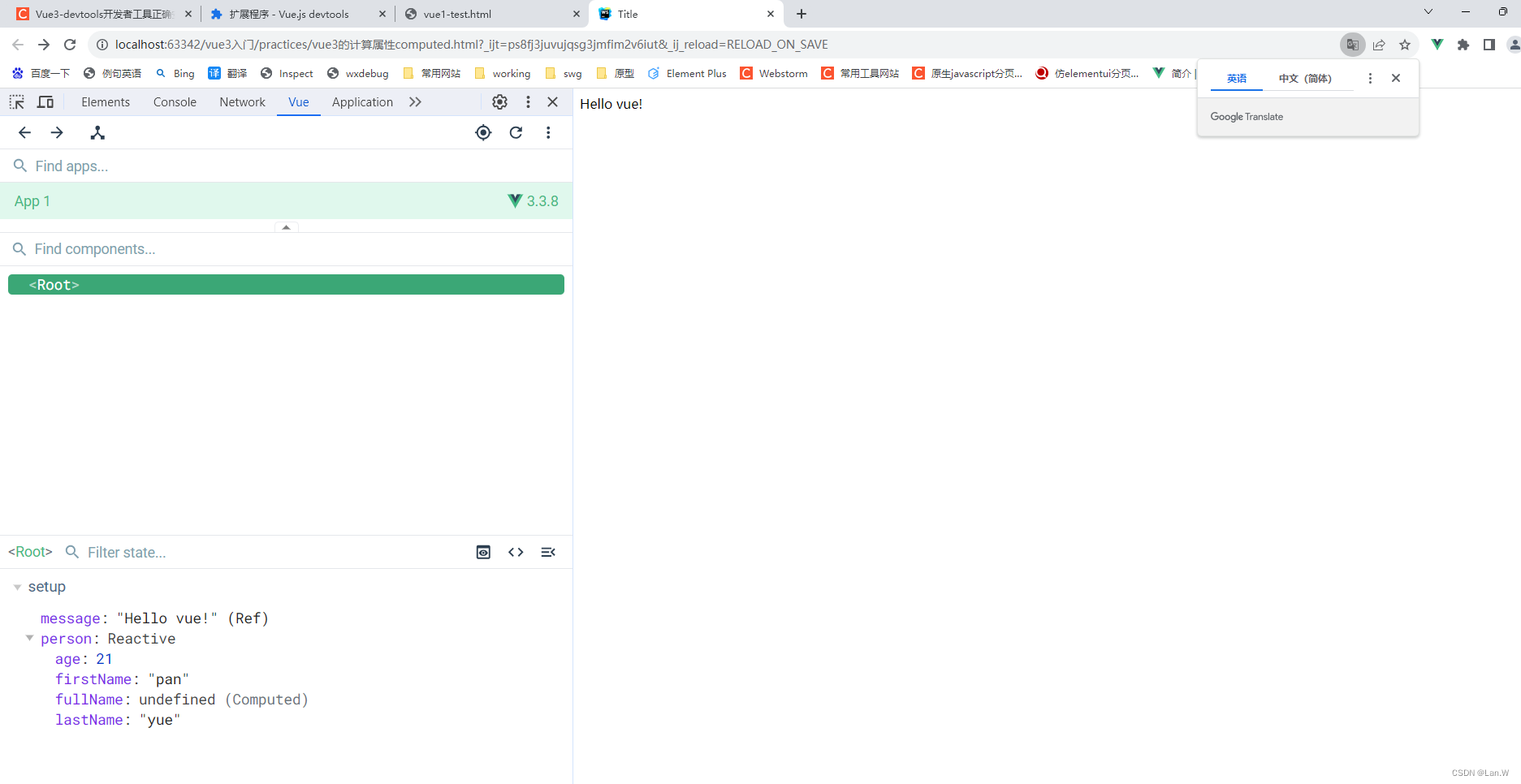
chrome 的vue3的开发者devtool不起作用
问题: 刚刚vue2升级到vue3,旧的devtool识别不了vue3数据。 原因: devtool版本过低。升级到最新。 解决: 去github下载vuetool项目代码: GitHub - vuejs/devtools: ⚙️ Browser devtools extension for debugging…...

Redis数据结构七之listpack和quicklist
本文首发于公众号:Hunter后端 原文链接:Redis数据结构七之listpack和quicklist 本篇笔记介绍 listpack 和 quicklist 两种结构 按照顺序,本来应该先介绍 quicklist 的结构,quicklist 在 7.0 之前的版本是由双向链表和压缩列表构成…...

单词规律问题
给定一种规律 pattern 和一个字符串 s ,判断 s 是否遵循相同的规律。 这里的 遵循 指完全匹配,例如, pattern 里的每个字母和字符串 s 中的每个非空单词之间存在着双向连接的对应规律。 示例1: 输入: pattern “abba”, s “dog cat cat d…...

蓝桥杯每日一题2023.11.8
题目描述 题目分析 对于输入的abc我们可以以a为年也可以以c为年,将abc,cab,cba这三种情况进行判断合法性即可,注意需要排序去重,所以考虑使用set 此处为纯模拟的写法,但使用循环代码会更加简洁。 方法一: #include&…...

高级PHP应用程序漏洞审核技术【一】
高级PHP应用程序漏洞审核技术【一】 目录 高级PHP应用程序漏洞审核技术【一】 本文章向大家介绍高级PHP应用程序漏洞审核技术【一】,主要内容包括其使用实例、应用技巧、基本知识点总结和需要注意事项,具有一定的参考价值,需要的朋友可以参…...
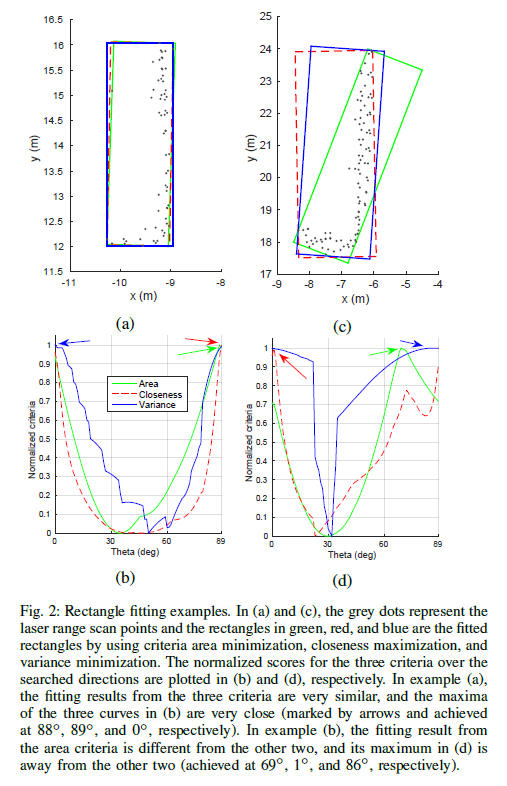
适用于4D毫米波雷达的目标矩形框聚类
目录 一、前言 二、点云聚类分割 三、基于方位搜索L型拟合 四、评价准则之面积最小化 五、评价准则之贴合最大化 六、评价准则之方差最小化 一、前言 对于多线束雷达可以获取目标物体更全面的面貌,在道路中前向或角雷达可能无法获取目标车矩形框但可以扫到两边…...
[模版总结] - 树的基本算法1 - 遍历
树结构定义 一种非线性存储结构,具有存储“一对多”关系的数据元素集合 种类 General Tree TrieB/B 树二叉树 满/完满/完全二叉树 完美BT : 除了叶子结点外所有节点都有两个字节点,每一层都完满填充完全BT: 除最后一层以外其他每一层都完美…...
macOS Sonoma 14.2beta2(23C5041e)发布(附黑白苹果镜像地址)
系统介绍 黑果魏叔11 月 10 日消息,今日向 Mac 电脑用户推送了 macOS 14.2 开发者预览版 Beta 2 更新(内部版本号:23C5041e),本次更新距离上次发布隔了 14 天。 macOS Sonoma 14.2 添加了 Music 收藏夹播放列表&…...
Docker进阶——再次认识docker的概念 Docker的结构 Docker镜像结构 镜像的构建方式
前言 在微服务大量应用的互联网时代,经常能看到docker的身影。作为docker的爱好者(在服务器安装MySQL,Redis。。。我用的都是docker),我也会持续深入学习和认识docker。 本篇博客再次介绍docker的基本概念࿰…...

postgis函数学习
1.特定功能的SQL 转为完整的json,前端调用用json_build_object、jsonb_agg等函数,处理mass_test表 select json_build_object(type,FetureCollection,features,jsonb_agg(st_asgeojson(mt.*)::json)) from mass_test mt获取图形边界范围的坐标 select…...
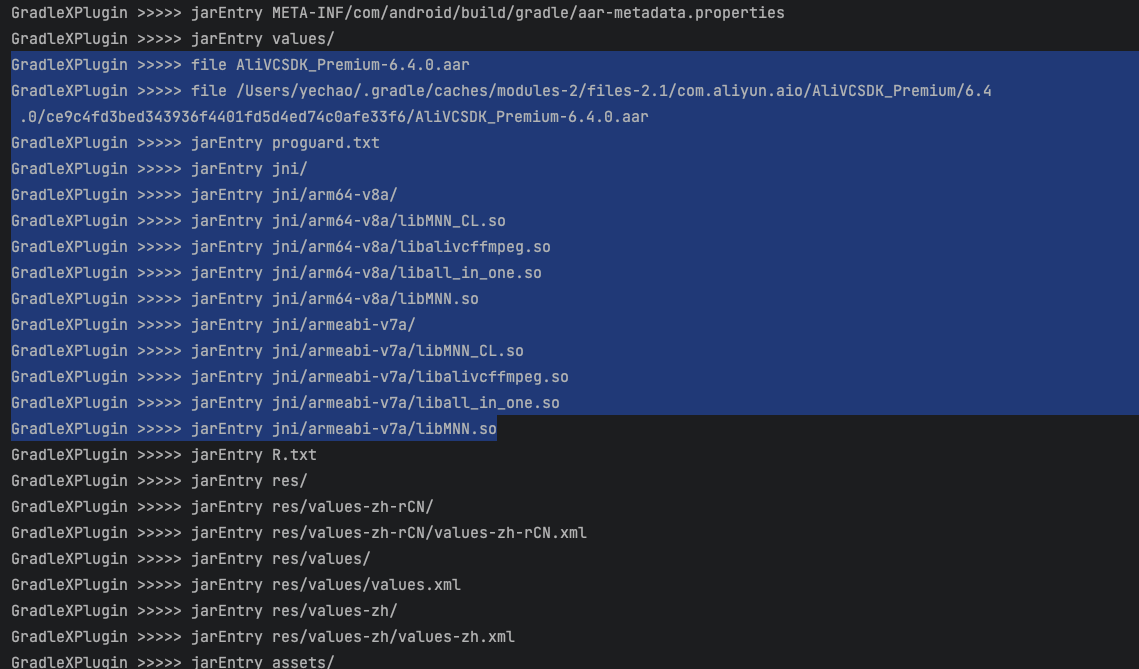
【Gradle-12】分析so文件和依赖的关系
1、前言 在包大小的占比中,so文件的占比往往是最高的,动辄几兆的大小多一个都会把包大小的指标打爆。 而在各厂商要求对手机CPU ARM架构进行分包适配的情况下,你更需要知道哪些依赖是没有适配v7a/v8a的,这将影响你的APP在应用市场…...
vue项目pdf文件的预览
1.下载 您可以在以下网址下载pdfjsLib:https://github.com/mozilla/pdf.js pdfjsLib是一个开源项目,您可以在GitHub上找到其源代码和相关资源。 2.放置文件位置 3.进入 在index.html引入 <script src"<% BASE_URL %>static/pdfjs-dist/b…...

企业计算机中了mkp勒索病毒怎么办,服务器中了勒索病毒如何处理
计算机技术的不断发展给企业的生产生活提供了极大便利,但也为企业带来了网络安全威胁。近期,云天数据恢复中心陆续接到很多企业的求助,企业的计算机服务器遭到了mkp勒索病毒攻击,导致企业的所有工作无法正常开展,给企业…...
Android拖放startDragAndDrop拖拽Glide加载堆叠圆角图,Kotlin(5)
Android拖放startDragAndDrop拖拽Glide加载堆叠圆角图,Kotlin(5) import android.content.ClipData import android.graphics.Canvas import android.graphics.Point import android.os.Bundle import android.util.Log import android.view.…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
