适用于4D毫米波雷达的目标矩形框聚类
目录
一、前言
二、点云聚类分割
三、基于方位搜索L型拟合
四、评价准则之面积最小化
五、评价准则之贴合最大化
六、评价准则之方差最小化
一、前言
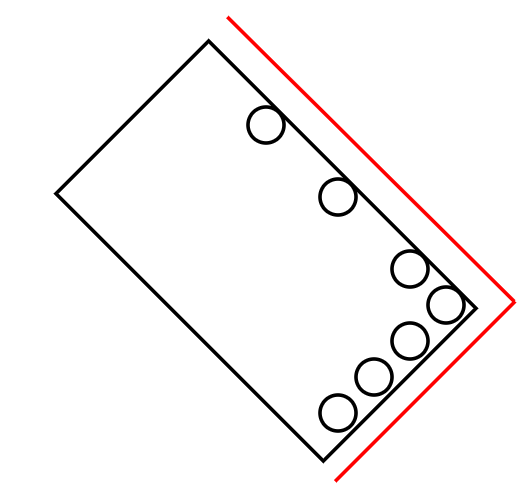
对于多线束雷达可以获取目标物体更全面的面貌,在道路中前向或角雷达可能无法获取目标车矩形框但可以扫到两边或者一边,在做目标方向估计时这些信息至关重要。看到一篇文章不错的思路,拿来记录借鉴下。
整体算法:
Step1: 将距离点按照预先设定的距离阈值进行聚类划分簇
Step2:基于方位搜索+特定准则进行L型拟合,得出4边参数
2.1 矩形面积最小化
2.2 点到边靠近最大化
2.3 点到边方差最小化
二、点云聚类分割
对于所有点,在距离r一点内找到它的相邻点,将相邻点设置为未检测,对未检测点继续找到距离r内的任何一个点,把邻近点放在这个簇中直到集群不再增长。

def _adoptive_range_segmentation(self, ox, oy):# Setup initial clustersegment_list = []for i, _ in enumerate(ox):c = set()r = self.R0 + self.Rd * np.linalg.norm([ox[i], oy[i]])for j, _ in enumerate(ox):d = np.hypot(ox[i] - ox[j], oy[i] - oy[j])if d <= r:c.add(j)segment_list.append(c)# Merge clusterwhile True:no_change = Truefor (c1, c2) in list(itertools.permutations(range(len(segment_list)), 2)):if segment_list[c1] & segment_list[c2]:segment_list[c1] = (segment_list[c1] | segment_list.pop(c2))no_change = Falsebreakif no_change:breakreturn segment_list
三、基于方位搜索L型拟合
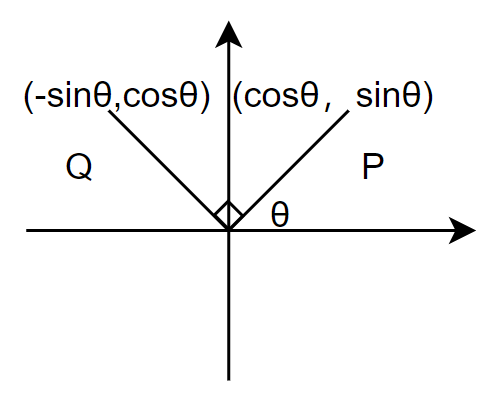
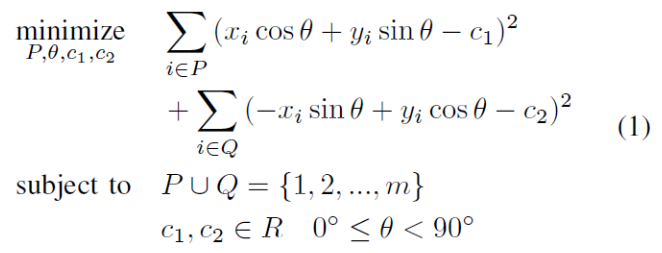
step2:基于方位搜索的L 型拟合
遍历矩形的所有可能方向;在每次迭代中,可以找到一个该方向并包含所有扫描点的矩形;进一步可以得到所有点到矩形四条边的距离,并根据这些距离将点分为P和Q,并计算相应的平方误差作为(1)中的目标函数;在迭代所有方向并获得所有相应的平方误差后,寻找实现最小平方误差的最优方向,并根据该方向拟合矩形

def _rectangle_search(self, x, y):xy = np.array([x, y]).Td_theta = np.deg2rad(self.d_theta_deg_for_search)min_cost = (-float('inf'), None)for theta in np.arange(0.0, np.pi / 2.0 - d_theta, d_theta):c = xy @ rot_mat_2d(theta)c1 = c[:, 0]c2 = c[:, 1]# Select criteriacost = 0.0if self.criteria == self.Criteria.AREA:cost = self._calc_area_criterion(c1, c2)elif self.criteria == self.Criteria.CLOSENESS:cost = self._calc_closeness_criterion(c1, c2)elif self.criteria == self.Criteria.VARIANCE:cost = self._calc_variance_criterion(c1, c2)if min_cost[0] < cost:min_cost = (cost, theta)# calc best rectanglesin_s = np.sin(min_cost[1])cos_s = np.cos(min_cost[1])c1_s = xy @ np.array([cos_s, sin_s]).Tc2_s = xy @ np.array([-sin_s, cos_s]).Trect = RectangleData()rect.a[0] = cos_srect.b[0] = sin_srect.c[0] = min(c1_s)rect.a[1] = -sin_srect.b[1] = cos_srect.c[1] = min(c2_s)rect.a[2] = cos_srect.b[2] = sin_srect.c[2] = max(c1_s)rect.a[3] = -sin_srect.b[3] = cos_srect.c[3] = max(c2_s)return rect
四、评价准则之面积最小化

def _calc_area_criterion(c1, c2):c1_max, c1_min, c2_max, c2_min = LShapeFitting._find_min_max(c1, c2)alpha = -(c1_max - c1_min) * (c2_max - c2_min)return alpha
五、评价准则之贴合最大化

def _calc_closeness_criterion(self, c1, c2):c1_max, c1_min, c2_max, c2_min = LShapeFitting._find_min_max(c1, c2)# Vectorizationd1 = np.minimum(c1_max - c1, c1 - c1_min)d2 = np.minimum(c2_max - c2, c2 - c2_min)d = np.maximum(np.minimum(d1, d2), self.min_dist_of_closeness_criteria)beta = (1.0 / d).sum()return beta六、评价准则之方差最小化

def _calc_variance_criterion(c1, c2):c1_max, c1_min, c2_max, c2_min = LShapeFitting._find_min_max(c1, c2)# Vectorizationd1 = np.minimum(c1_max - c1, c1 - c1_min)d2 = np.minimum(c2_max - c2, c2 - c2_min)e1 = d1[d1 < d2]e2 = d2[d1 >= d2]v1 = - np.var(e1) if len(e1) > 0 else 0.v2 = - np.var(e2) if len(e2) > 0 else 0.gamma = v1 + v2return gamma
Result:
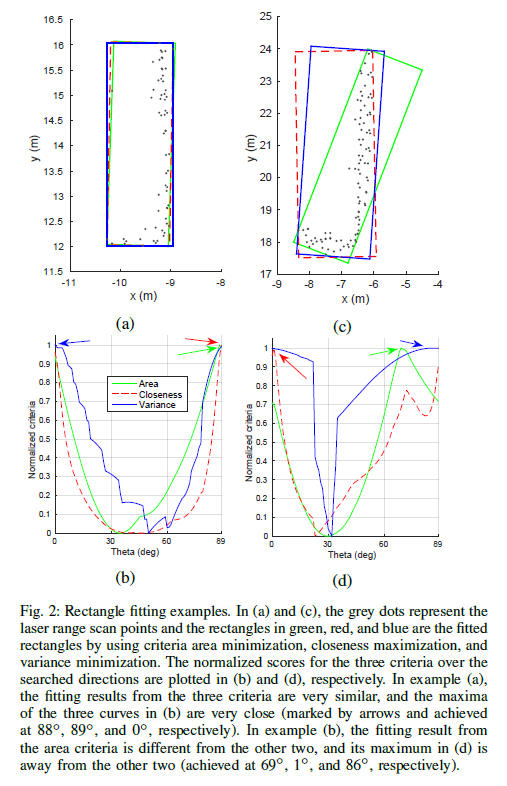
参考:《Efficient L-Shape Fitting for Vehicle Detection Using Laser Scanners》
相关文章:

适用于4D毫米波雷达的目标矩形框聚类
目录 一、前言 二、点云聚类分割 三、基于方位搜索L型拟合 四、评价准则之面积最小化 五、评价准则之贴合最大化 六、评价准则之方差最小化 一、前言 对于多线束雷达可以获取目标物体更全面的面貌,在道路中前向或角雷达可能无法获取目标车矩形框但可以扫到两边…...
[模版总结] - 树的基本算法1 - 遍历
树结构定义 一种非线性存储结构,具有存储“一对多”关系的数据元素集合 种类 General Tree TrieB/B 树二叉树 满/完满/完全二叉树 完美BT : 除了叶子结点外所有节点都有两个字节点,每一层都完满填充完全BT: 除最后一层以外其他每一层都完美…...
macOS Sonoma 14.2beta2(23C5041e)发布(附黑白苹果镜像地址)
系统介绍 黑果魏叔11 月 10 日消息,今日向 Mac 电脑用户推送了 macOS 14.2 开发者预览版 Beta 2 更新(内部版本号:23C5041e),本次更新距离上次发布隔了 14 天。 macOS Sonoma 14.2 添加了 Music 收藏夹播放列表&…...
Docker进阶——再次认识docker的概念 Docker的结构 Docker镜像结构 镜像的构建方式
前言 在微服务大量应用的互联网时代,经常能看到docker的身影。作为docker的爱好者(在服务器安装MySQL,Redis。。。我用的都是docker),我也会持续深入学习和认识docker。 本篇博客再次介绍docker的基本概念࿰…...

postgis函数学习
1.特定功能的SQL 转为完整的json,前端调用用json_build_object、jsonb_agg等函数,处理mass_test表 select json_build_object(type,FetureCollection,features,jsonb_agg(st_asgeojson(mt.*)::json)) from mass_test mt获取图形边界范围的坐标 select…...
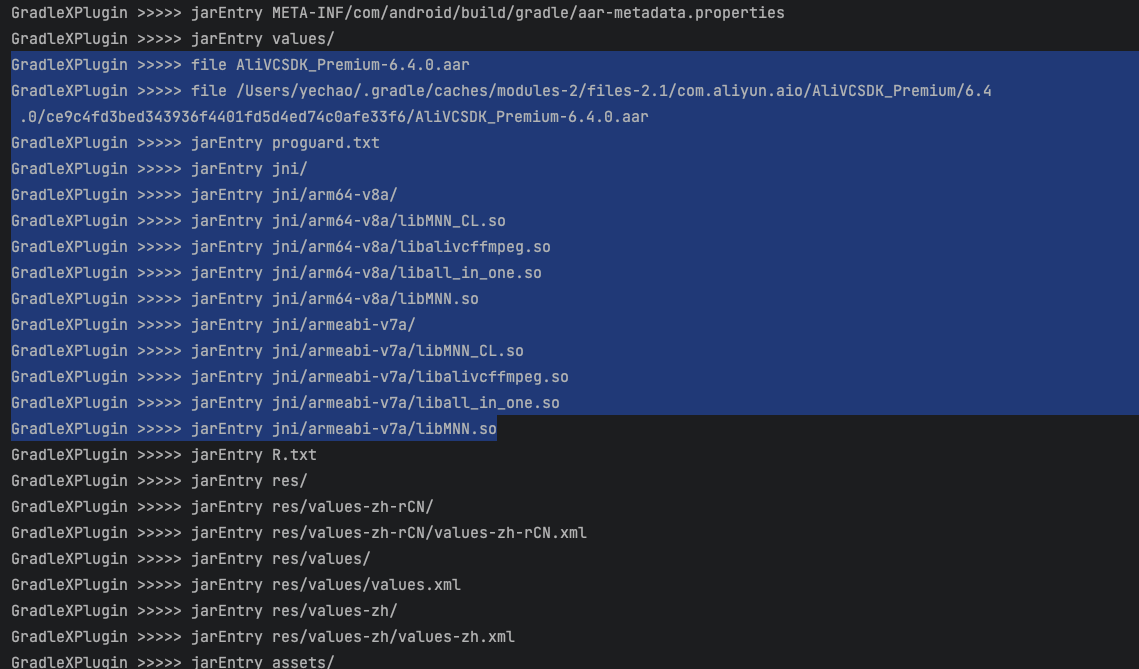
【Gradle-12】分析so文件和依赖的关系
1、前言 在包大小的占比中,so文件的占比往往是最高的,动辄几兆的大小多一个都会把包大小的指标打爆。 而在各厂商要求对手机CPU ARM架构进行分包适配的情况下,你更需要知道哪些依赖是没有适配v7a/v8a的,这将影响你的APP在应用市场…...
vue项目pdf文件的预览
1.下载 您可以在以下网址下载pdfjsLib:https://github.com/mozilla/pdf.js pdfjsLib是一个开源项目,您可以在GitHub上找到其源代码和相关资源。 2.放置文件位置 3.进入 在index.html引入 <script src"<% BASE_URL %>static/pdfjs-dist/b…...

企业计算机中了mkp勒索病毒怎么办,服务器中了勒索病毒如何处理
计算机技术的不断发展给企业的生产生活提供了极大便利,但也为企业带来了网络安全威胁。近期,云天数据恢复中心陆续接到很多企业的求助,企业的计算机服务器遭到了mkp勒索病毒攻击,导致企业的所有工作无法正常开展,给企业…...
Android拖放startDragAndDrop拖拽Glide加载堆叠圆角图,Kotlin(5)
Android拖放startDragAndDrop拖拽Glide加载堆叠圆角图,Kotlin(5) import android.content.ClipData import android.graphics.Canvas import android.graphics.Point import android.os.Bundle import android.util.Log import android.view.…...

1994-2021年分行业二氧化碳排放量数据
1994-2021年分行业二氧化碳排放量数据 1、时间:1994-2021年 2、来源:原始数据整理自能源年鉴 3、指标:统计年度、行业代码、行业名称、煤炭二氧化碳排放量、焦炭二氧化碳排放量、原油二氧化碳排放量、汽油二氧化碳排放量、煤油二氧化碳排放…...

如何进行Go程序的打包发布
上一篇,我们已经用GoLand开发了第一个程序Hello Kitty,接下去,我们将完成Go程序的打包发布。 执行: go build -x main.gogo build 和 go run 在编译过程中其实是差不多的,不同之处是 go build 会生成编译好二进制文件并删掉编译…...

python工具HIKVISION视频编码设备接入网关任意文件下载
python工具 构造payload /serverLog/downFile.php?fileName../web/html/serverLog/downFile.php漏洞证明 文笔生疏,措辞浅薄,望各位大佬不吝赐教,万分感谢。 免责声明:由于传播或利用此文所提供的信息、技术或方法而造成的任何…...
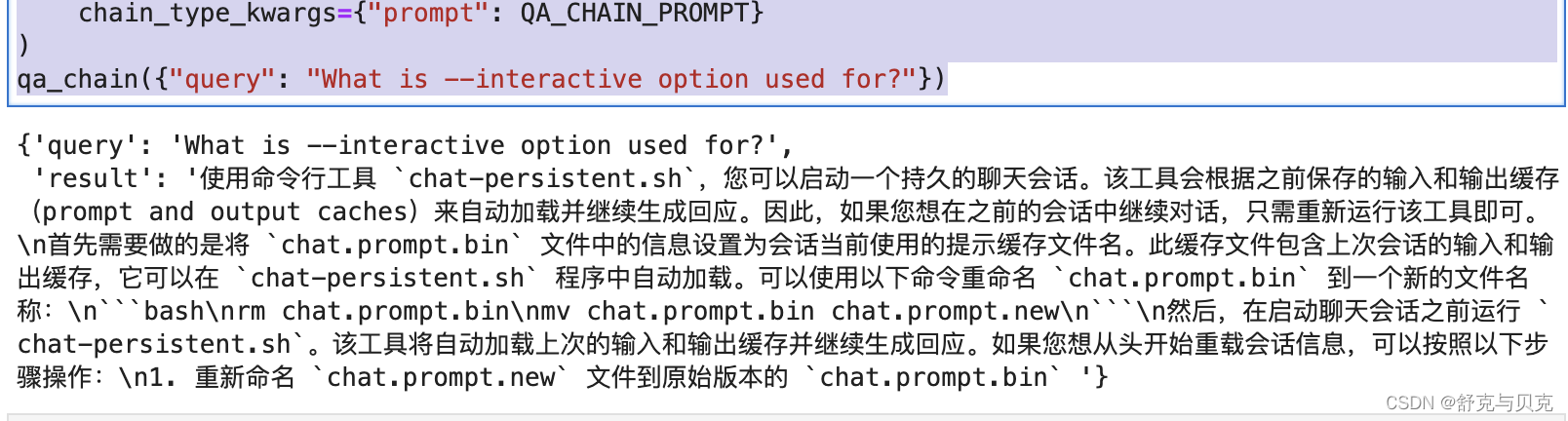
[NLP] 使用Llama.cpp和LangChain在CPU上使用大模型
一 准备工作 下面是构建这个应用程序时将使用的软件工具: 1.Llama-cpp-python 下载llama-cpp, llama-cpp-python [NLP] Llama2模型运行在Mac机器-CSDN博客 2、LangChain LangChain是一个提供了一组广泛的集成和数据连接器,允许我们链接和编排不同的模块。可以常…...

开发知识点-Ant-Design-Vue
Ant-Design-Vue a-input a-input Vue组件 a-spin 加载中的效果 data字段 mounted钩子函数 Ant Design Vue 组件库 list-type“picture-card” 上传的图片作为卡片展示 name show-upload-list action :beforeUpload“handleBeforeUpload” :headers“customHeaders” :disabl…...
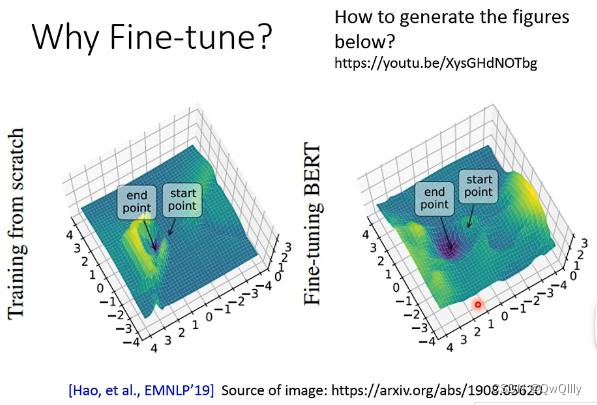
2022最新版-李宏毅机器学习深度学习课程-P50 BERT的预训练和微调
模型输入无标签文本(Text without annotation),通过消耗大量计算资源预训练(Pre-train)得到一个可以读懂文本的模型,在遇到有监督的任务是微调(Fine-tune)即可。 最具代表性是BERT&…...
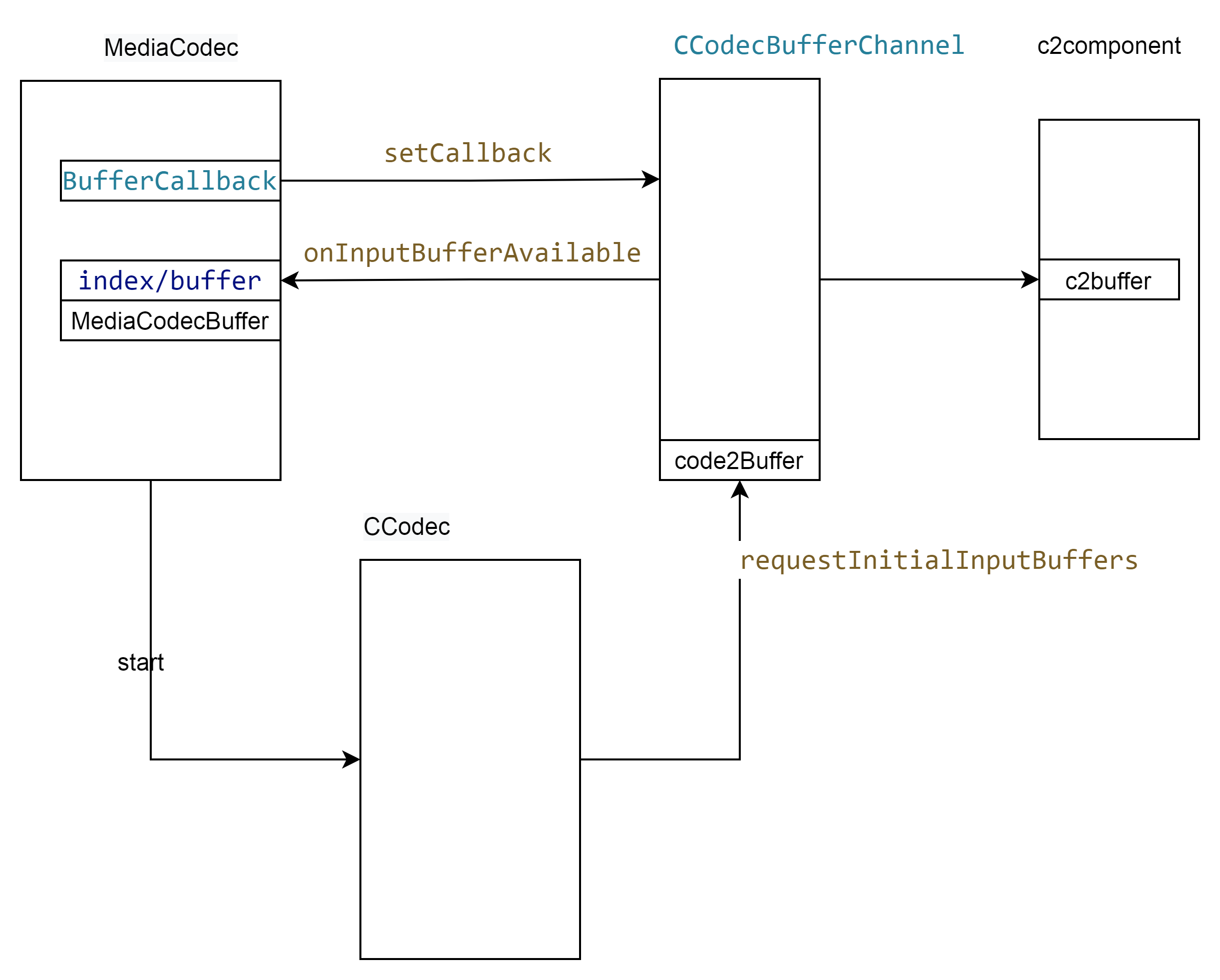
Android codec2 视频框架 之输入buffer
文章目录 输入端的内存管理输入数据包buffer结构体的转换 主要的流程如上, 申请内存在CCodecBufferChannel,申请之后回调到MediaCodec。然后应用从MediaCodec获取 将解码数据放到buffer中,CCodecBufferChannel在将这块buffer 送到componet模块…...

Python实现局部二进制算法(LBP)
1.介绍 局部二进制算法是一种用于获取图像纹理的算法。这算法可以应用于人脸识别、纹理分类、工业检测、遥感图像分析、动态纹理识别等领域。 2.示例 """ 局部二进制算法,计算图像纹理特征 """ import cv2 import numpy as np imp…...

如何评价现在的CSGO游戏搬砖市场
如何评价现在的csgo市场? 其实整个搬砖市场,现在已经变得乌烟瘴气,散发着“恶臭”。我个人非常鄙视那些虚有其表,大小通吃的做法,那些甚至连搬砖数据都看不懂的人,也出来吹嘘着“实力强大,经验丰…...

ResourceQuota对象在K8s上的说明
ResourceQuota资源对象的说明,以及在集群中的作用说明 定义说明 https://kubernetes.io/zh-cn/docs/concepts/policy/resource-quotas/ 集群中的资源组的划分和设计 在具有 32 GiB 内存和 16 核 CPU 资源的集群中,允许 A 团队使用 20 GiB 内存 和 10 核…...

悟空crm二次开发 增加客户保护功能 (很久没有消息,但是有觉得有机会的客户)就进入了保护转态
需求:客户信息录入不限数量,但是录入的信息1个月内只有自己和部门领导能看到,如果1个月内未成交或者未转移至自己的客保 则掉入公海所有人可见,这里所说的客保就是现在系统自带的客保 1、需求思维导图 2、新增保护按钮 3、点击该…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
