代码随想录算法训练营Day 49 || 123.买卖股票的最佳时机III 、188.买卖股票的最佳时机IV
123.买卖股票的最佳时机III
力扣题目链接(opens new window)
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
-
示例 1:
-
输入:prices = [3,3,5,0,0,3,1,4]
-
输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3。
-
示例 2:
-
输入:prices = [1,2,3,4,5]
-
输出:4 解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
-
示例 3:
-
输入:prices = [7,6,4,3,1]
-
输出:0 解释:在这个情况下, 没有交易完成, 所以最大利润为0。
-
示例 4:
-
输入:prices = [1] 输出:0
提示:
- 1 <= prices.length <= 10^5
- 0 <= prices[i] <= 10^5
解题思路:
-
定义状态: 由于最多可以进行两笔交易,我们需要跟踪四个状态:第一次买入(
first_buy)、第一次卖出(first_sell)、第二次买入(second_buy)、第二次卖出(second_sell)。 -
初始化状态:
first_buy初始化为负无穷大,因为还没有进行任何买入操作。first_sell、second_buy、second_sell都初始化为0,因为初始利润为0。
-
状态转移:
- 对于每一天的价格,更新上述四个状态。
first_buy:选择之前的first_buy或者当天的价格(负数,因为是花费)中的较大者。first_sell:选择之前的first_sell或者今天的价格加上first_buy(代表卖出)中的较大者。second_buy:选择之前的second_buy或者first_sell减去今天的价格中的较大者。second_sell:选择之前的second_sell或者今天的价格加上second_buy中的较大者。
-
计算结果:
- 遍历完所有价格后,
second_sell就是最大利润。
- 遍历完所有价格后,
class Solution:def maxProfit(self, prices: List[int]) -> int:if not prices:return 0first_buy, first_sell = -float('inf'), 0second_buy, second_sell = -float('inf'), 0for price in prices:first_buy = max(first_buy, -price) # 第一次买入的最佳选择first_sell = max(first_sell, first_buy + price) # 第一次卖出的最佳选择second_buy = max(second_buy, first_sell - price) # 第二次买入的最佳选择second_sell = max(second_sell, second_buy + price) # 第二次卖出的最佳选择return second_sell # 返回最大利润
188.买卖股票的最佳时机IV
力扣题目链接
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
-
示例 1:
-
输入:k = 2, prices = [2,4,1]
-
输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2。
-
示例 2:
-
输入:k = 2, prices = [3,2,6,5,0,3]
-
输出:7 解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4。随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
提示:
- 0 <= k <= 100
- 0 <= prices.length <= 1000
- 0 <= prices[i] <= 1000
解题思路:
-
状态定义: 定义
dp[i][j]作为一个二维数组,其中i表示天数,j表示交易次数(每次交易包括买和卖两个动作)。dp[i][j]表示第i天完成j笔交易能获得的最大利润。 -
初始化:
- 对于
dp[0][..](即第0天),无论交易次数如何,利润都是0,因为没有交易发生。 - 对于
dp[..][0](即没有交易),无论天数如何,利润都是0。
- 对于
-
状态转移:
- 需要决定第
i天是买入、卖出还是不操作。这可以通过比较不同选择下的利润来决定。 - 对于买入操作,我们要找到之前某天
m,使得dp[m][j-1] - prices[i](即第m天完成j-1笔交易后的利润减去第i天的股价)最大。 - 对于卖出操作,我们要找到之前某天
m,使得dp[m][j-1] + prices[i]最大。 - 对于不操作,直接保持前一天的状态,即
dp[i][j] = dp[i-1][j]。
- 需要决定第
-
结果计算:
- 最后
dp[n-1][k](其中n是天数)就是在给定的条件下可以获得的最大利润。
- 最后
class Solution:def maxProfit(self, k: int, prices: List[int]) -> int:if not prices:return 0n = len(prices)if k >= n // 2:return self.maxProfitInf(prices)dp = [[0] * (k + 1) for _ in range(n)]for j in range(1, k + 1):max_diff = -prices[0]for i in range(1, n):dp[i][j] = max(dp[i-1][j], prices[i] + max_diff)max_diff = max(max_diff, dp[i-1][j-1] - prices[i])return dp[-1][-1]def maxProfitInf(self, prices: List[int]) -> int:profit = 0for i in range(1, len(prices)):if prices[i] > prices[i-1]:profit += prices[i] - prices[i-1]return profit
相关文章:

代码随想录算法训练营Day 49 || 123.买卖股票的最佳时机III 、188.买卖股票的最佳时机IV
123.买卖股票的最佳时机III 力扣题目链接(opens new window) 给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。 设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。 注意:你不能同时参与多笔交易(你必须…...

threejs(11)-精通着色器编程(难点)2
一、shader着色器编写高级图案 小日本国旗 precision lowp float; varying vec2 vUv; float strength step(0.5,distance(vUv,vec2(0.5))0.25) ; gl_FragColor vec4(strength,strength,strength,strength);绘制圆 precision lowp float; varying vec2 vUv; float strength 1…...

配置cuda和cudnn出现 libcudnn.so.8 is not a symbolic link问题
cuda版本为11.2 问题如图所示: 解决办法: sudo ln -sf /usr/local/cuda-11.2/targets/x86_64-linux/lib/libcudnn_adv_train.so.8.1.1 /usr/local/cuda-11.2/targets/x86_64-linux/lib/libcudnn_adv_train.so.8 sudo ln -sf /usr/local/cuda-11.2/targ…...

“目标值排列匹配“和“背包组合问题“的区别和leetcode例题详解
1 目标值排列匹配 1.1 从目标字符串的角度来看,LC139是一个排列问题,因为最终目标子串的各个字符的顺序是固定的? 当我们从目标字符串 s 的角度来看 LC139 “单词拆分” 问题,确实可以认为它涉及到排列的概念,但这种…...

火星加载WMTS服务
这是正常的加载瓦片 http://192.168.1.23:8008/geoserver/mars3d/gwc/service/wmts?tilematrixEPSG%3A4326%3A7&layermars3d%3Abuffer&style&tilerow46&tilecol197&tilematrixsetEPSG%3A4326&formatimage%2Fpng&serviceWMTS&version1.0.0&…...
为什么要学习去使用云服务器,外网 IP能干什么,MAC使用Termius连接阿里云服务器。保姆级教学
目录 引言 可能有人想问为什么要学习云服务器? (获取Linux环境,获得外网IP) 二、安装教程 引言 可能有人想问为什么要学习云服务器? (获取Linux环境,获得外网IP) 1.虚拟机(下策) …...
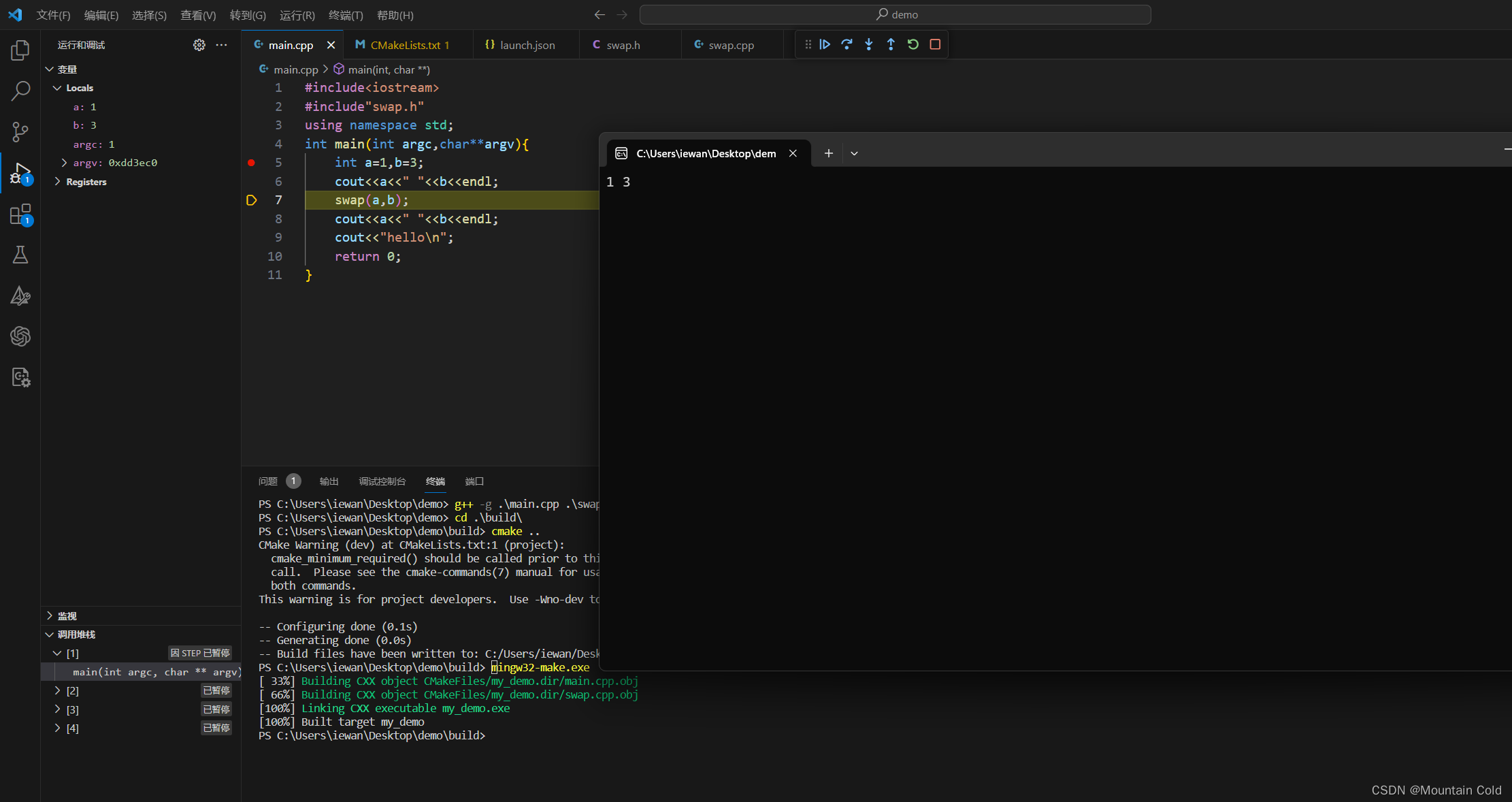
VS c++多文件编译
前言:记录下我这个菜鸡学习的过程,如有错误恳请指出,不胜感激! 1.简单多文件编译调试 文件目录: 编译: -g选项是告诉编译器生成调试信息,这样可以在程序崩溃或出现错误时更容易地进行调试。这…...
)
JVM关键指标监控(调优)
JVM 99%情况下不需要调优 使用性能更好的垃圾回收器 核心指标 针对单台服务器而言: jvm.gc.time: 每分钟GC耗时在1s以内 500ms以内最佳 jvm.gc.meantime: 每次YGC耗时在100ms以内,50ms以内最佳 jvm.fullgc.count: FGC(老生代垃圾回收)最多几小时1次&…...
【Proteus仿真】【Arduino单片机】LCD1602-IIC液晶显示
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真Arduino单片机控制器,使用PCF8574、LCD1602液晶等。 主要功能: 系统运行后,LCD1602液晶显示各种效果。 二、软件设计 /* 作者:嗨小…...

skynet学习笔记03— 服务
01、API newservice(name, ...): 阻塞的形势启动一个名为 name 的新服务,待start函数执行完后会返回这个服务的地址。uniqueservice(name, ...):针对于当前节点,启动一个唯一服务(相当于单例),…...
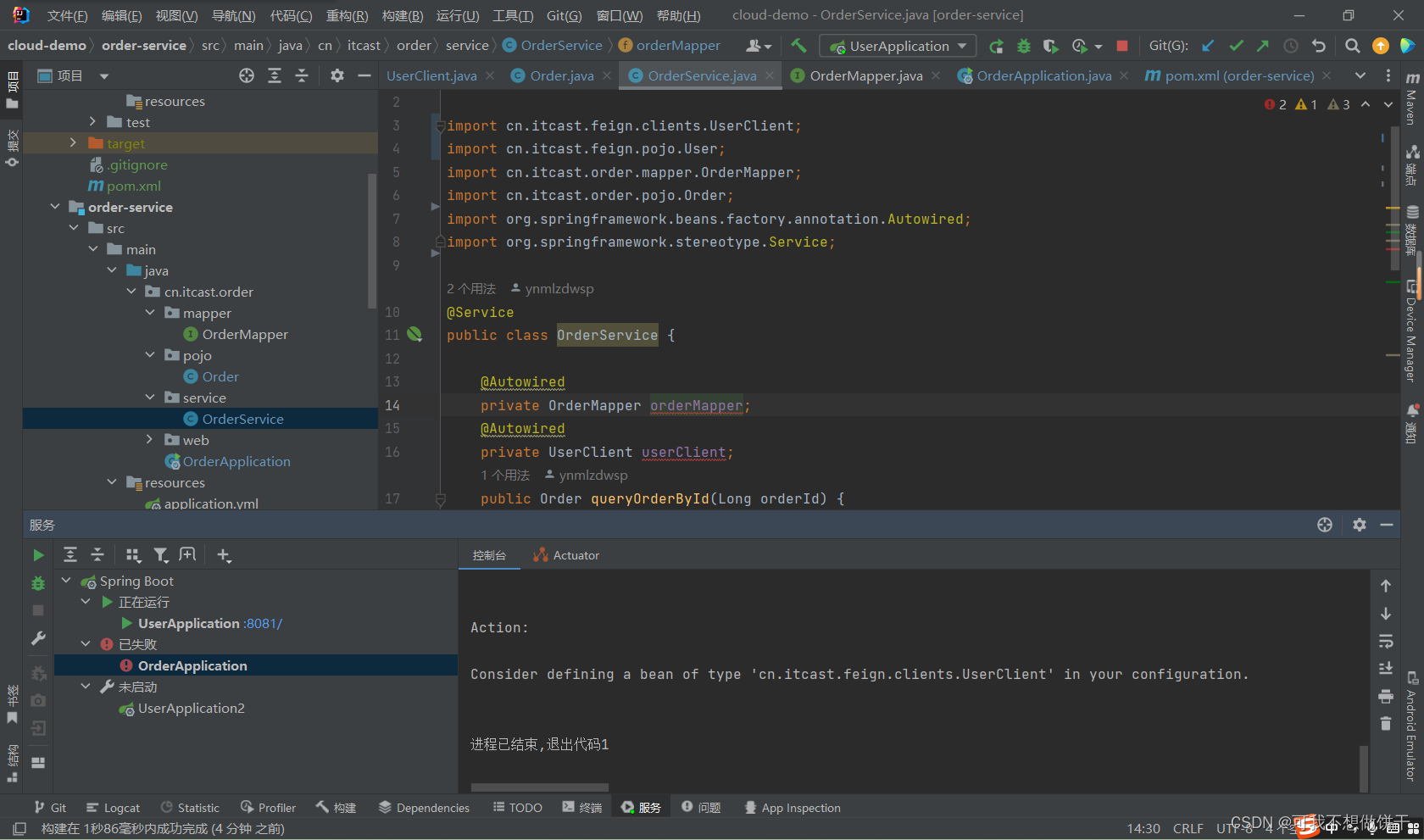
34 Feign最佳实践
2.4.2.抽取方式 将Feign的Client抽取为独立模块,并且把接口有关的POJO、默认的Feign配置都放到这个模块中,提供给所有消费者使用。 例如,将UserClient、User、Feign的默认配置都抽取到一个feign-api包中,所有微服务引用该依赖包…...
软文推广中如何搭建媒体矩阵
媒体矩阵简单理解就是在不同的媒体平台上,根据运营目标和需求,建立起全面系统的媒体布局,进行多平台同步运营。接下来媒介盒子就来和大家聊聊,企业在软文推广过程中为什么需要搭建媒体矩阵,又该如何搭建媒体矩阵。 一、…...

Unity地面交互效果——5、角色足迹的制作
大家好,我是阿赵。 之前几篇文章,已经介绍了地面交互的轨迹做法。包括了法线、曲面细分还有顶点偏移。Shader方面的内容已经说完了,不过之前都是用一个球来模拟轨迹,这次来介绍一下,怎样和角色动作结合,…...

Centos8安装出错问题
科普介绍: CentOS 8 是一个基于 Linux 的操作系统,是 Red Hat Enterprise Linux (RHEL)的免费和开源版本。它提供了稳定、安全和可靠的基础设施,适用于服务器和桌面环境。CentOS 8 是 CentOS 系列中最新的版本&#x…...

计算机网络技术
深入浅出计算机网络 微课视频_哔哩哔哩_bilibili 第一章概述 1.1 信息时代的计算机网络 1. 计算机网络各类应用 2. 计算机网络带来的负面问题 3. 我国互联网发展情况 1.2 因特网概述 1. 网络、互连网(互联网)与因特网的区别与关系 如图所示࿰…...
)
当电脑桌面黑屏,而你只有一个鼠标该怎么办(重启方法的平替)
作为一个打工人 电脑是不是黑屏简直是routine了 我们都知道重启能解决一切问题 但是!! 如果你只有一个鼠标 电脑因为种种原因没法重启 该怎么办呢? 别慌 下面的方法非常灵验 1.按住ctrlShiftEsc 调出任务管理器;此项为必须…...
Leetcode2833. 距离原点最远的点
Every day a Leetcode 题目来源:2833. 距离原点最远的点 解法1:贪心 要使得到达的距离原点最远的点,就看 left 和 right 谁大,将 left 和 right 作为矢量相加,再往同方向加上 underline。 答案即为 abs(left - rig…...
chrome 的vue3的开发者devtool不起作用
问题: 刚刚vue2升级到vue3,旧的devtool识别不了vue3数据。 原因: devtool版本过低。升级到最新。 解决: 去github下载vuetool项目代码: GitHub - vuejs/devtools: ⚙️ Browser devtools extension for debugging…...

Redis数据结构七之listpack和quicklist
本文首发于公众号:Hunter后端 原文链接:Redis数据结构七之listpack和quicklist 本篇笔记介绍 listpack 和 quicklist 两种结构 按照顺序,本来应该先介绍 quicklist 的结构,quicklist 在 7.0 之前的版本是由双向链表和压缩列表构成…...

单词规律问题
给定一种规律 pattern 和一个字符串 s ,判断 s 是否遵循相同的规律。 这里的 遵循 指完全匹配,例如, pattern 里的每个字母和字符串 s 中的每个非空单词之间存在着双向连接的对应规律。 示例1: 输入: pattern “abba”, s “dog cat cat d…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
