“目标值排列匹配“和“背包组合问题“的区别和leetcode例题详解
1 目标值排列匹配
1.1 从目标字符串的角度来看,LC139是一个排列问题,因为最终目标子串的各个字符的顺序是固定的?
当我们从目标字符串 s 的角度来看 LC139 “单词拆分” 问题,确实可以认为它涉及到排列的概念,但这种排列是在一个更宏观的层面上,而不是在我们通常讨论组合和排列问题时所指的那种。
1.1.1 排列的角度
在 “单词拆分” 问题中,目标字符串 s 的字符顺序是固定的。我们不能改变这些字符的顺序。我们的任务是确定是否可以通过字典中的单词(这些单词的内部字符顺序也是固定的)来构造出这个特定顺序的字符串。从这个角度看,确实涉及到了字符的“排列”——但这是指字符串 s 和字典中单词的内部字符顺序,而不是字典中单词作为整体的排列顺序。
1.1.2 组合的角度
然而,当我们讨论解决这个问题的算法时,我们通常将其视为一个组合问题。这是因为我们关心的是如何从字典中选择单词(并且可以重复选择)来构造字符串 s,而不是这些单词的选择顺序。我们可以以任何顺序检查和组合这些单词,只要它们最终能组合成目标字符串 s。
1.1.3 动态规划的应用
在动态规划的应用中,我们通常关注的是如何逐步构建目标字符串,并在每一步检查是否可以使用字典中的单词来形成当前长度的子串。这种方法更侧重于组合(即哪些单词被选中来构造子串)而不是单词的选择顺序。
1.1.4 总结
因此,虽然从目标字符串 s 的角度来看,LC139 “单词拆分” 涉及到字符的排列,但在解决问题的算法层面,它更像是一个组合问题。这是因为我们关注的是如何从字典中选择单词来构造字符串 s,而不是这些单词的选择顺序。
1.1 Leetcode139. 单词拆分

public boolean wordBreak(String s, List<String> wordDict) {int n=s.length();char[]cs=s.toCharArray();int m=wordDict.size();HashSet<String>set=new HashSet<>(wordDict);boolean[]f=new boolean[n+1];f[0]=true;for(int i=1;i<=n;i++){for(int j=0;j<i;j++){if(f[j]&&set.contains(s.substring(j,i))){f[i]=true;break;}}}return f[n];}
2 背包组合问题
基本上背包问题无论从目标值角度还是元素列表角度都是组合问题
2.1 leetcode题目集合
细数Leetcode上的背包问题
相关文章:

“目标值排列匹配“和“背包组合问题“的区别和leetcode例题详解
1 目标值排列匹配 1.1 从目标字符串的角度来看,LC139是一个排列问题,因为最终目标子串的各个字符的顺序是固定的? 当我们从目标字符串 s 的角度来看 LC139 “单词拆分” 问题,确实可以认为它涉及到排列的概念,但这种…...

火星加载WMTS服务
这是正常的加载瓦片 http://192.168.1.23:8008/geoserver/mars3d/gwc/service/wmts?tilematrixEPSG%3A4326%3A7&layermars3d%3Abuffer&style&tilerow46&tilecol197&tilematrixsetEPSG%3A4326&formatimage%2Fpng&serviceWMTS&version1.0.0&…...
为什么要学习去使用云服务器,外网 IP能干什么,MAC使用Termius连接阿里云服务器。保姆级教学
目录 引言 可能有人想问为什么要学习云服务器? (获取Linux环境,获得外网IP) 二、安装教程 引言 可能有人想问为什么要学习云服务器? (获取Linux环境,获得外网IP) 1.虚拟机(下策) …...
VS c++多文件编译
前言:记录下我这个菜鸡学习的过程,如有错误恳请指出,不胜感激! 1.简单多文件编译调试 文件目录: 编译: -g选项是告诉编译器生成调试信息,这样可以在程序崩溃或出现错误时更容易地进行调试。这…...
)
JVM关键指标监控(调优)
JVM 99%情况下不需要调优 使用性能更好的垃圾回收器 核心指标 针对单台服务器而言: jvm.gc.time: 每分钟GC耗时在1s以内 500ms以内最佳 jvm.gc.meantime: 每次YGC耗时在100ms以内,50ms以内最佳 jvm.fullgc.count: FGC(老生代垃圾回收)最多几小时1次&…...
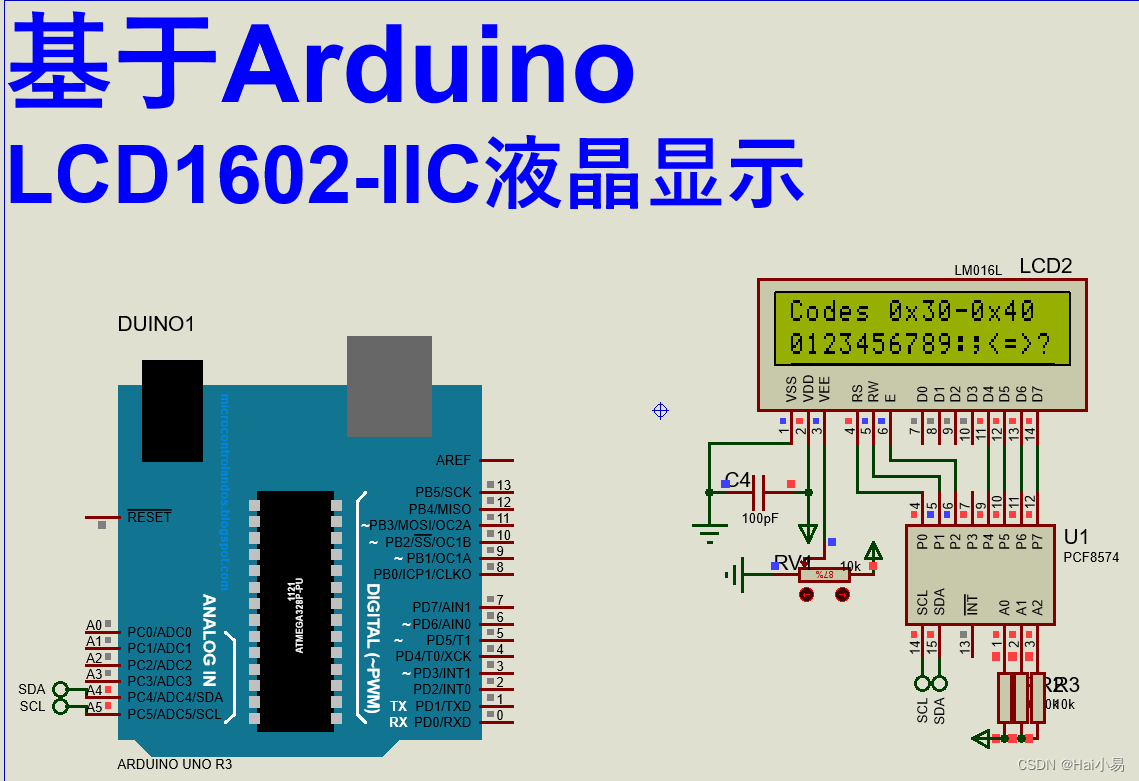
【Proteus仿真】【Arduino单片机】LCD1602-IIC液晶显示
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真Arduino单片机控制器,使用PCF8574、LCD1602液晶等。 主要功能: 系统运行后,LCD1602液晶显示各种效果。 二、软件设计 /* 作者:嗨小…...

skynet学习笔记03— 服务
01、API newservice(name, ...): 阻塞的形势启动一个名为 name 的新服务,待start函数执行完后会返回这个服务的地址。uniqueservice(name, ...):针对于当前节点,启动一个唯一服务(相当于单例),…...
34 Feign最佳实践
2.4.2.抽取方式 将Feign的Client抽取为独立模块,并且把接口有关的POJO、默认的Feign配置都放到这个模块中,提供给所有消费者使用。 例如,将UserClient、User、Feign的默认配置都抽取到一个feign-api包中,所有微服务引用该依赖包…...
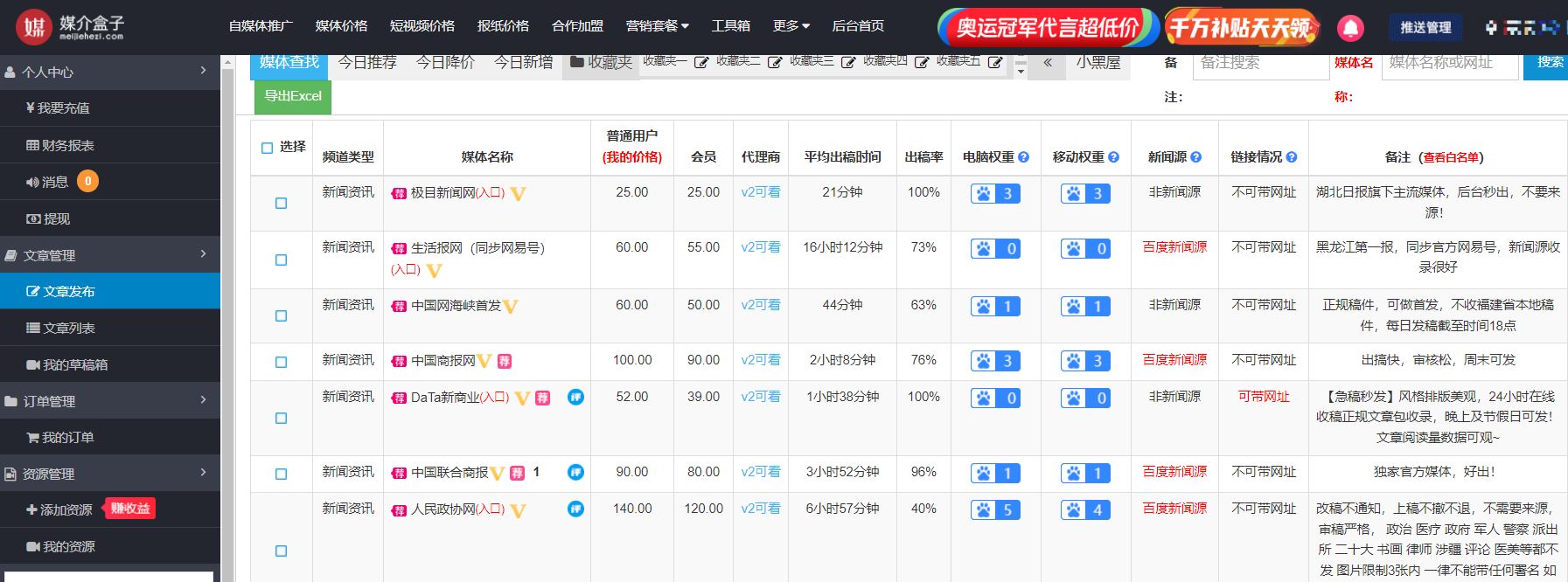
软文推广中如何搭建媒体矩阵
媒体矩阵简单理解就是在不同的媒体平台上,根据运营目标和需求,建立起全面系统的媒体布局,进行多平台同步运营。接下来媒介盒子就来和大家聊聊,企业在软文推广过程中为什么需要搭建媒体矩阵,又该如何搭建媒体矩阵。 一、…...

Unity地面交互效果——5、角色足迹的制作
大家好,我是阿赵。 之前几篇文章,已经介绍了地面交互的轨迹做法。包括了法线、曲面细分还有顶点偏移。Shader方面的内容已经说完了,不过之前都是用一个球来模拟轨迹,这次来介绍一下,怎样和角色动作结合,…...

Centos8安装出错问题
科普介绍: CentOS 8 是一个基于 Linux 的操作系统,是 Red Hat Enterprise Linux (RHEL)的免费和开源版本。它提供了稳定、安全和可靠的基础设施,适用于服务器和桌面环境。CentOS 8 是 CentOS 系列中最新的版本&#x…...

计算机网络技术
深入浅出计算机网络 微课视频_哔哩哔哩_bilibili 第一章概述 1.1 信息时代的计算机网络 1. 计算机网络各类应用 2. 计算机网络带来的负面问题 3. 我国互联网发展情况 1.2 因特网概述 1. 网络、互连网(互联网)与因特网的区别与关系 如图所示࿰…...
)
当电脑桌面黑屏,而你只有一个鼠标该怎么办(重启方法的平替)
作为一个打工人 电脑是不是黑屏简直是routine了 我们都知道重启能解决一切问题 但是!! 如果你只有一个鼠标 电脑因为种种原因没法重启 该怎么办呢? 别慌 下面的方法非常灵验 1.按住ctrlShiftEsc 调出任务管理器;此项为必须…...
Leetcode2833. 距离原点最远的点
Every day a Leetcode 题目来源:2833. 距离原点最远的点 解法1:贪心 要使得到达的距离原点最远的点,就看 left 和 right 谁大,将 left 和 right 作为矢量相加,再往同方向加上 underline。 答案即为 abs(left - rig…...
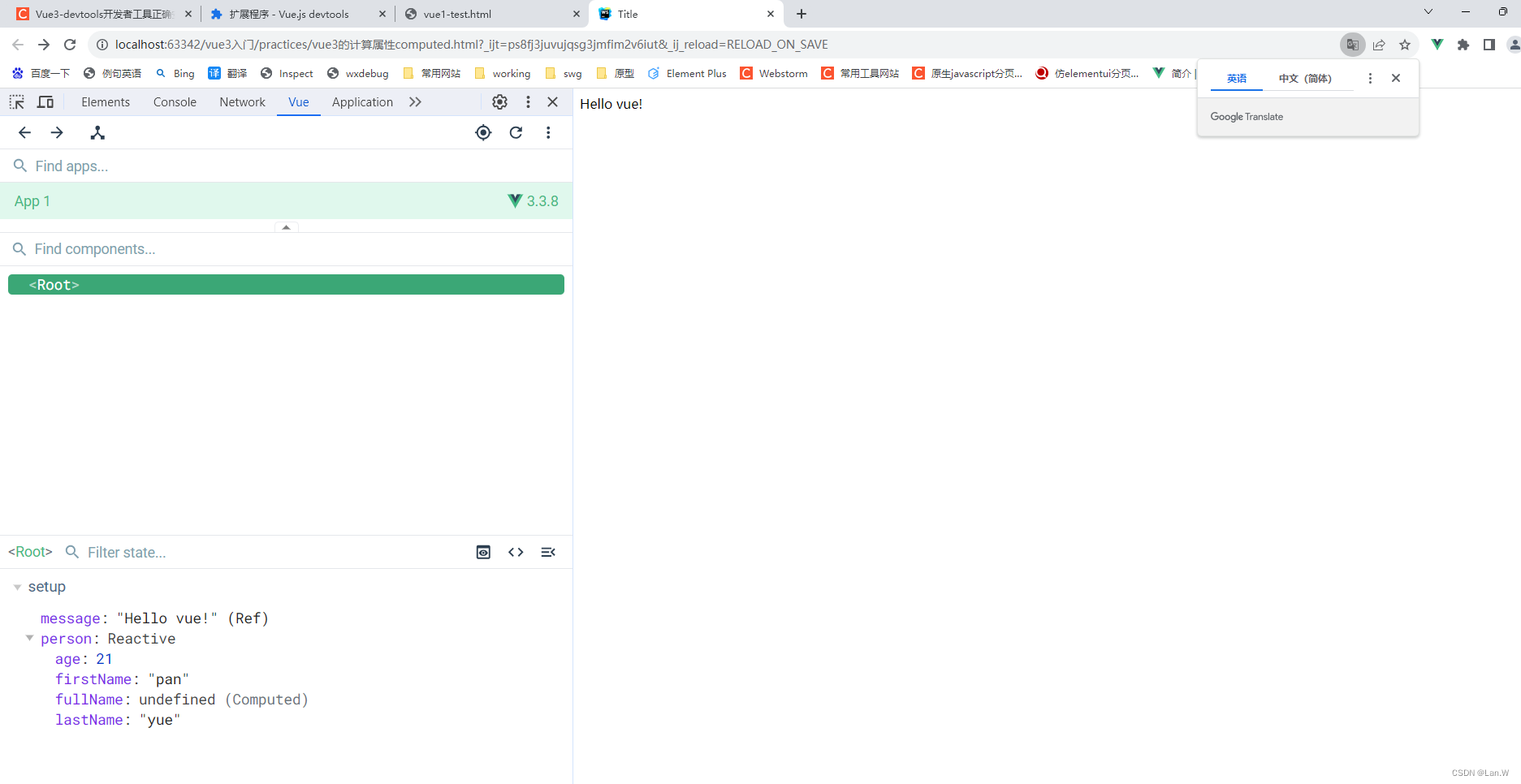
chrome 的vue3的开发者devtool不起作用
问题: 刚刚vue2升级到vue3,旧的devtool识别不了vue3数据。 原因: devtool版本过低。升级到最新。 解决: 去github下载vuetool项目代码: GitHub - vuejs/devtools: ⚙️ Browser devtools extension for debugging…...

Redis数据结构七之listpack和quicklist
本文首发于公众号:Hunter后端 原文链接:Redis数据结构七之listpack和quicklist 本篇笔记介绍 listpack 和 quicklist 两种结构 按照顺序,本来应该先介绍 quicklist 的结构,quicklist 在 7.0 之前的版本是由双向链表和压缩列表构成…...

单词规律问题
给定一种规律 pattern 和一个字符串 s ,判断 s 是否遵循相同的规律。 这里的 遵循 指完全匹配,例如, pattern 里的每个字母和字符串 s 中的每个非空单词之间存在着双向连接的对应规律。 示例1: 输入: pattern “abba”, s “dog cat cat d…...

蓝桥杯每日一题2023.11.8
题目描述 题目分析 对于输入的abc我们可以以a为年也可以以c为年,将abc,cab,cba这三种情况进行判断合法性即可,注意需要排序去重,所以考虑使用set 此处为纯模拟的写法,但使用循环代码会更加简洁。 方法一: #include&…...

高级PHP应用程序漏洞审核技术【一】
高级PHP应用程序漏洞审核技术【一】 目录 高级PHP应用程序漏洞审核技术【一】 本文章向大家介绍高级PHP应用程序漏洞审核技术【一】,主要内容包括其使用实例、应用技巧、基本知识点总结和需要注意事项,具有一定的参考价值,需要的朋友可以参…...
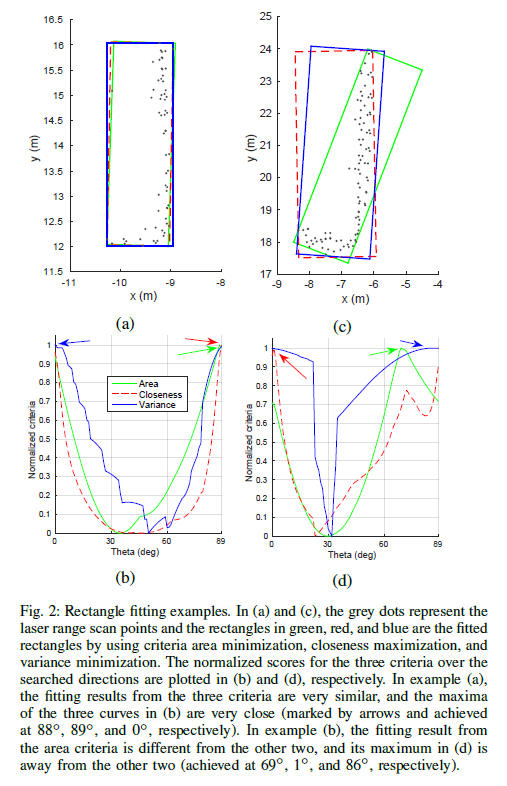
适用于4D毫米波雷达的目标矩形框聚类
目录 一、前言 二、点云聚类分割 三、基于方位搜索L型拟合 四、评价准则之面积最小化 五、评价准则之贴合最大化 六、评价准则之方差最小化 一、前言 对于多线束雷达可以获取目标物体更全面的面貌,在道路中前向或角雷达可能无法获取目标车矩形框但可以扫到两边…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
