[蓝桥杯复盘] 第 3 场双周赛20231111
[蓝桥杯复盘] 第 3 场双周赛20231111
- 总结
- 深秋的苹果
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 鲜花之海
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 斐波拉契跳跃
- 2. 思路分析
- 3. 代码实现
- 星石传送阵
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
总结
- 做了后4题。https://www.lanqiao.cn/oj-contest/challenge-3/
- T5 二分
- T6 数学公式
- T7 博弈
- T8 优化建图+dij
深秋的苹果
链接: 深秋的苹果
1. 题目描述

2. 思路分析
- 二分即可。但这题上界很大,无脑1e18会wa,实测2e18能过。
3. 代码实现
# ms
def solve():n, m = RI()arr = RILST()p = s = 0for v in arr:p += v*ss += vdef ok(x):cnt = 1s = c =0for v in arr:c += v * ss += vif c > x:c = 0s = vcnt += 1if cnt > m:return Falsereturn Trueprint(lower_bound(0, p, key=ok))# print(lower_bound(0, 2*10**18, key=ok))
鲜花之海
链接: 鲜花之海
1. 题目描述

2. 思路分析
- 画一下矩阵图,发现按照和可以分为左上半区和右下半区,是一个分段函数。
- 那么分类讨论,看看k落在第几条↙斜线上,由于是等差数列求和,需要解一元二次方程。
3. 代码实现
"""
x*(x+1)//2 <= k
x^2 + x - k*2<= 0
x <= (-1 +- sqrt(1 + 4 * k*2))/2(n-1+n-1-x+1)*x//2 <= k
"""# ms
def solve():n, k = RI()left = (1 + n - 1) * (n - 1) // 2mid = nif k <= left + mid:x = int((-1 + sqrt(1 + 4 * k * 2)) / 2)s = x * (x + 1) // 2h = x + 1if s == k:print(h - 1, 1)else:h += 1k -= sprint(k, h - k)else:k -= left + mid# print(left,mid,k)x = int((2 * n - 1 - sqrt((2 * n - 1) ** 2 - 4 * 2 * k)) / 2)s = (n - 1 + n - 1 - x + 1) * x // 2# print(x,s)h = n + x + 1if s == k:print(n, h - n)else:h += 1k -= s# print(x,h,k)print(2 + x + k - 1, h - (2 + x + k - 1))
斐波拉契跳跃
链接: 斐波拉契跳跃
2. 思路分析
- 博弈题优先考虑记忆化搜索。
- 这题转移和状态都是走斐波那契数列的,所以状态和转移都很少,因此可以过。
3. 代码实现
fib = [0, 1, 2]
while fib[-1] <= 10 ** 5:fib.append(fib[-1] + fib[-2])
pfib = {v: i for i, v in enumerate(fib)}# ms
def solve():n, = RI()a = RILST()pos = [0] * nfor i, v in enumerate(a):pos[v - 1] = i@lru_cache(None)def dfs(p, d): # 从p位置出发,上一步长d时,能否赢for v in fib[pfib[d] + 1:]:if v >= n: breakif p + v < n and a[p + v] > a[p]:if not dfs(p + v, v): # 对方不能赢return Trueif p - v >= 0 and a[p - v] > a[p]:if not dfs(p - v, v):return Truereturn Falsefor st in range(n):print(['Little Qiao', 'Little Lan'][dfs(st, 0)])
星石传送阵
链接: 星石传送阵

2. 思路分析
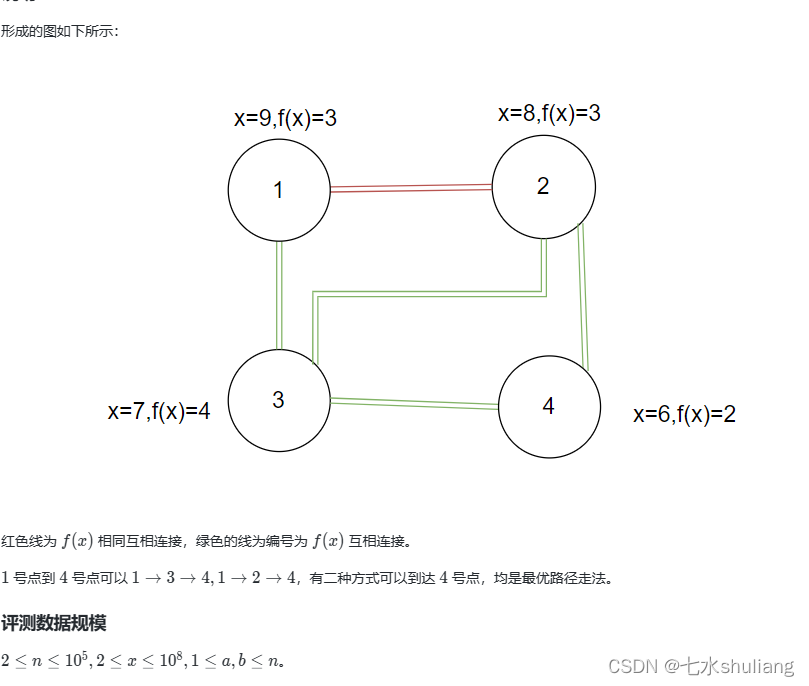
- 题面太乱了,省流:每个位置i的f(x)是x分解质因数求和modn+1;i和f可以互达;f相同的i也可以互达。问a到b最短路。
- 那么由于有很多节点的f可能是相同的,他们都可以互达的话就是稠密图,考虑增加中间虚拟节点连接他们。
- 由于f是对n取模后+1的,那么新节点可以用[n+1,2n]这些节点。
- 那么u->f->v这算1次跳跃,每条边边权应该是0.5;正常互条的节点边权是1;实现时全部乘2避免处理浮点数。
- 另一种思路,按f分组,直接BFS,可以省去一个log。
- bfs时,对每个节点处理本组f记录的邻居后,直接移除这整个组,因为他们已经访问过了。这样就可以避免稠密图的边过多造成的TLE。
3. 代码实现
class PrimeTable:def __init__(self, n: int) -> None:self.n = nself.primes = primes = [] # 所有n以内的质数self.min_div = min_div = [0] * (n + 1) # md[i]代表i的最小(质)因子min_div[1] = 1# 欧拉筛O(n),顺便求出min_divfor i in range(2, n + 1):if not min_div[i]:primes.append(i)min_div[i] = ifor p in primes:if i * p > n: breakmin_div[i * p] = pif i % p == 0:breakdef prime_factorization(self, x: int):"""分解质因数,复杂度1. 若x>n则需要从2模拟到sqrt(x),如果中间x降到n以下则走2;最坏情况,不含低于n的因数,则需要开方复杂度2. 否则x质因数的个数,那么最多就是O(lgx)"""n, min_div = self.n, self.min_divfor p in range(2, int(x ** 0.5) + 1):if x <= n: breakif x % p == 0:cnt = 0while x % p == 0: cnt += 1; x //= pyield p, cntwhile 1 < x <= n:p, cnt = min_div[x], 0while x % p == 0: cnt += 1; x //= pyield p, cntif x >= n and x > 1:yield x, 1pt = PrimeTable(10 ** 6)def solve():n, a, b = RI()arr = RILST()g = [[] for _ in range(2 * n + 3)]for i, v in enumerate(arr, start=1):f = sum(x * y for x, y in pt.prime_factorization(v)) % n + 1ff = f + n + 1 # 跳到虚拟节点,边权0.5,实际处理边权全部乘2g[ff].append((i, 1))g[i].append((ff, 1))if f <= n: # 互跳节点g[i].append((f, 2))g[f].append((i, 2))q = [(0, a)]dis = [inf] * (2 * n + 3)dis[a] = 0while q:# print(q)c, u = heappop(q)if c > dis[u]: continueif u == b:return print(c // 2)for v, w in g[u]:if c + w < dis[v]:dis[v] = c + wheappush(q, (c + w, v))print(-1)
六、参考链接
- 无
相关文章:

[蓝桥杯复盘] 第 3 场双周赛20231111
[蓝桥杯复盘] 第 3 场双周赛20231111 总结深秋的苹果1. 题目描述2. 思路分析3. 代码实现 鲜花之海1. 题目描述2. 思路分析3. 代码实现 斐波拉契跳跃2. 思路分析3. 代码实现 星石传送阵2. 思路分析3. 代码实现 六、参考链接 总结 做了后4题。https://www.lanqiao.cn/oj-contes…...
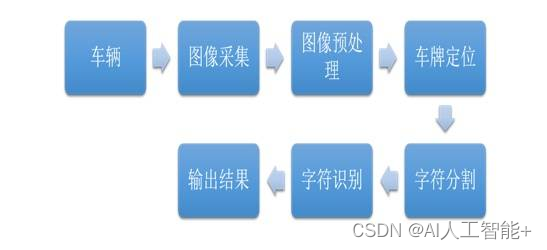
浅析移动端车牌识别技术的工作原理及其过程
随着社会经济的发展与汽车的日益普及带来巨大的城市交通压力,在此背景下,智能交通系统成为解决这一问题的关键。而在提出发展无线智能交通系统后,作为智能交通的核心,车牌识别系统需要开始面对车牌识别移动化的现实需求。基于实现车牌识别移动化这一目标,一种基于Android移动终…...

计算机网络期末复习-Part4
1、UDP和TCP的比较 TCP提供可靠传输;UDP提供不可靠传输。TCP有连接;UDP无连接(减小时延)。TCP提供流量控制;UDP不提供流量控制。TCP提供拥塞控制;UDP不提供拥塞控制(传输快)。TCP提…...
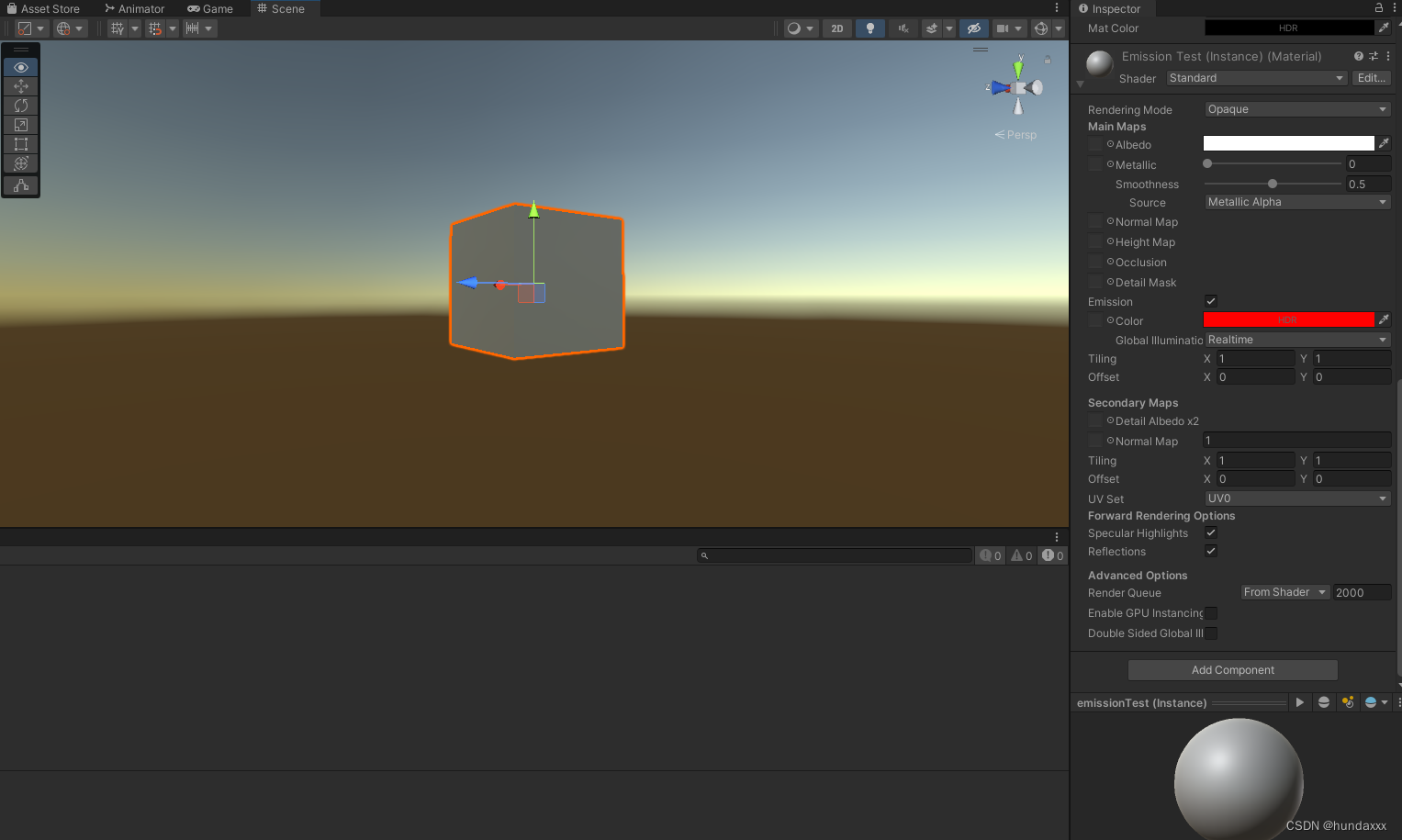
解决EnableKeyword(“_Emission“)运行状态不起作用
我使用的是Standard Shader,一开始“_Emission”没有开启 当我运行下面的代码,可以看到Inspector窗口已经生效,然而物体本身并没有重新开始渲染,反射没有开启 public GameObject go; // Start is called before the first frame…...

管理能力测评,如何提升管理能力?
管理能力是综合能力的体现,通常也解读为组织管理能力,如果要再细分的话,可能还包括有沟通能力,协调能力,组织能力,执行力和专业能力等等。不过没有办法说的太细节,因为每个部分铺开了都是一个独…...

基于工业智能网关的汽车充电桩安全监测方案
近年来,我国新能源汽车产业得到快速发展,电动车产量和销量都在持续增长,不仅国内市场竞争激烈,而且也远销海外,成为新的经济增长点。但与此同时,充电设施的运营却面临着安全和效率的双重挑战。 当前的充电桩…...

基于JavaWeb+SpringBoot+微信小程序的酒店商品配送平台系统的设计和实现
基于JavaWebSpringBoot微信小程序的酒店商品配送平台系统的设计和实现 源码传送入口前言主要技术系统设计功能截图Lun文目录订阅经典源码专栏Java项目精品实战案例《500套》 源码获取 源码传送入口 前言 本章内容概括了基于微信小程序的酒店商品配送平台的可行性分析、系统功…...

Android修行手册-POI操作Excel实现超链接并且变为蓝色
点击跳转>Unity3D特效百例点击跳转>案例项目实战源码点击跳转>游戏脚本-辅助自动化点击跳转>Android控件全解手册点击跳转>Scratch编程案例点击跳转>软考全系列 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&…...
:Halcon导出c#脚本)
Halcon WPF 开发学习笔记(2):Halcon导出c#脚本
文章目录 前言HalconC#教学简单说明如何二开机器视觉 前言 我目前搜了一下我了解的机器视觉软件,有如下特点 优点缺点兼容性教学视频(B站前三播放量)OpenCV开源,免费,因为有源码所以适合二次开发学习成本极高,卡学历。研究生博士…...
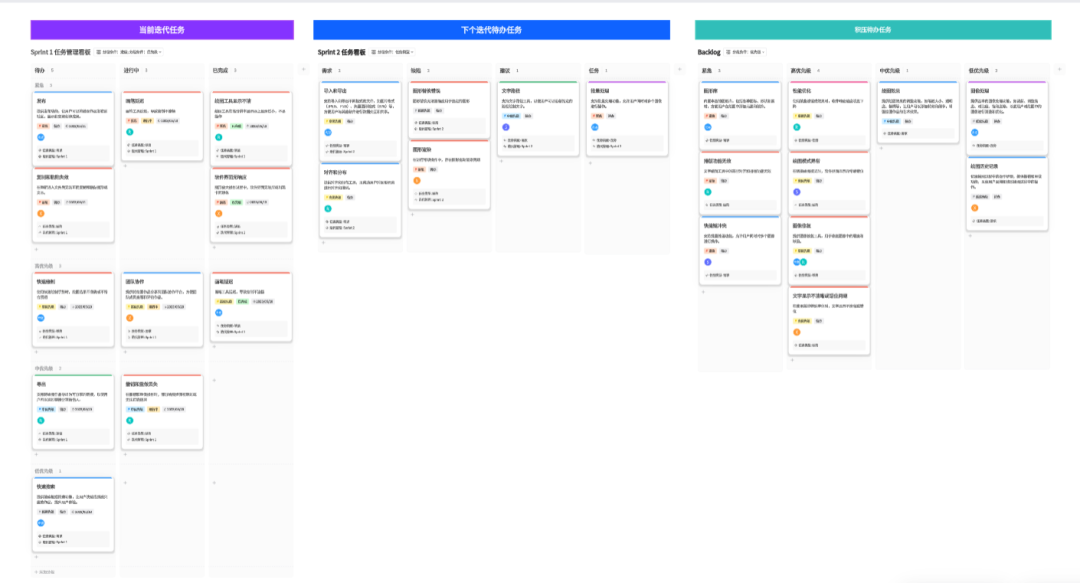
Scrum敏捷开发全流程,3款必备的项目管理工具!
Scrum是一种敏捷方法,致力于帮助团队高效地协作和完成复杂的项目。它强调迭代和快速迭代、自组织、快速响应变化等原则,使得项目开发变得更加灵活和高效。 在Scrum敏捷开发过程中,项目管理工具是必不可少的。下面介绍3款常用的敏捷开发工具…...
基于Quartz实现动态定时任务
生命无罪,健康万岁,我是laity。 我曾七次鄙视自己的灵魂: 第一次,当它本可进取时,却故作谦卑; 第二次,当它在空虚时,用爱欲来填充; 第三次,在困难和容易之…...
-41)
hdlbits系列verilog解答(计算向量中1出现次数)-41
文章目录 一、问题描述二、verilog源码三、仿真结果一、问题描述 “频次计数”电路对输入向量中的“1”数进行计数。为 255 位输入向量构建频次计数电路。 Module Declaration module top_module( input [254:0] in, output [7:0] out ); 二、verilog源码 module top_module…...
)
2023年最新的前端面试收集(1)
2023年最新的前端面试收集 一、你在项目中做的性能优化的事情有哪些网络优化页面渲染优化JS优化图片优化webpack打包优化vue优化react优化 二、webworker中为什么能提升js执行的性能三、微前端 一、你在项目中做的性能优化的事情有哪些 网络优化 DNS预解析 link标签的rel属性设…...

flutter实现上拉加载下拉刷新
效果如下: flutter实现上拉加载下拉刷新 使用到的库是easy_refresh 安装请查看官网 接口用的是提供的接口https://reqres.in/ 请求接口用到的库是dio 下面主要是介绍如何使用easy_refresh实现上拉加载数据,详细学习其它例子请查看easy_refresh main…...
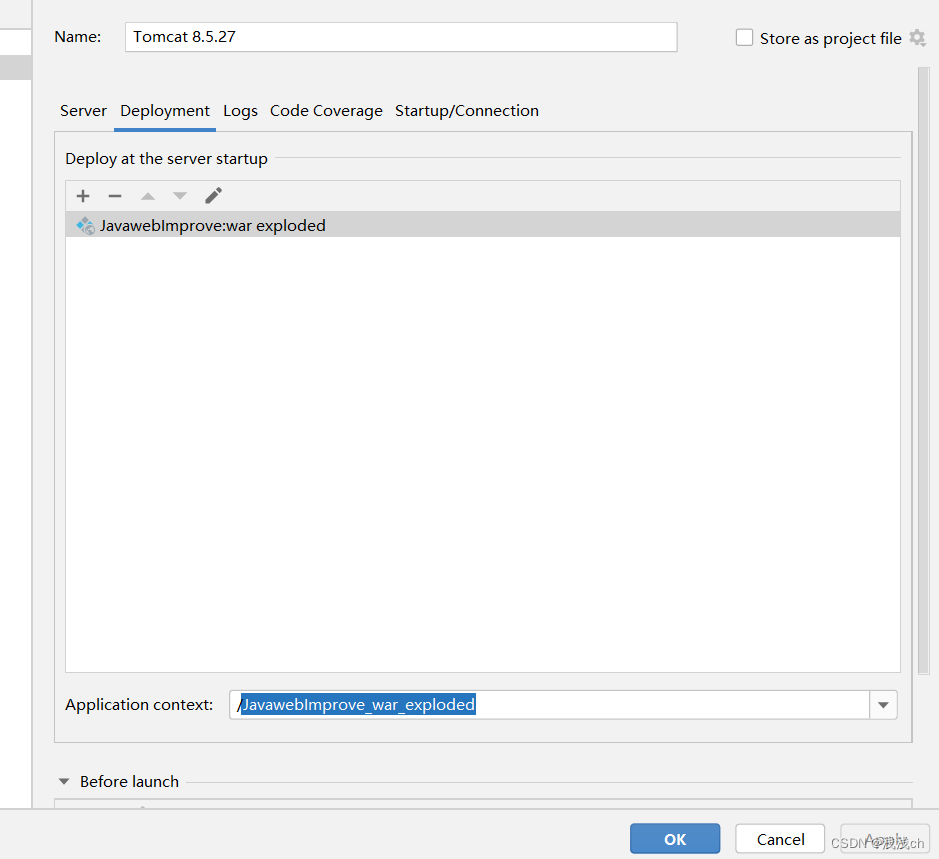
tomcat+idea--如何在idea上发布项目
对应于idea2022以后的版本 (一)如何配置idea上的tomcat? 1、新建一个项目,左上角File,new,project,新建后就和普通的java项目一样。 2、然后点击项目名,右键选择“Add framework s…...
考研数据结构单链表的增删改查看这一篇就够了
目录 一. 单链表的特点 1.1 解引用拓展 🤖 二. 单链表的操作 2.1不带头节点的操作 2.1.1 打印 2.1.1.1 创建结点 2.1.2 尾插(需要二级指针) 注意形参的值不改变实参:(精髓部分) 2.1.3 头插 2.1.4…...

Windows查看端口占用情况
Windows如何查看端口占用情况 方法1. cmd命令行执行netstat命令,查看端口占用情况 netstat -ano 以上命令输出太多信息,不方便查看,通过如下命令搜索具体端口占用情况,例如:8080端口 netstat -ano | findstr "…...
Python:词法分析(行结构与显式、隐式行拼接)
相关阅读 Pythonhttps://blog.csdn.net/weixin_45791458/category_12403403.html?spm1001.2014.3001.5482 1、逻辑结构 一个Python程序由许多逻辑行组成,字面意义上的一行指的是末尾有换行符(\n),但在不同的情况下,行末尾的换行符(\n)可能有…...

前端Vue 结合xlxs库实现解析excel文件,并动态组装表头!
目录 1.前言2.数据定义3. 页面布局4.上传之前的事件5.解析excel文件,并组装系统表头与excel表头的对应关系6.下拉框改变事件 1.前言 最近有一个需求,就是用户可以任意导入一个自定义的excel文件,让用户可以自己选择,组装表头的对应关系&…...
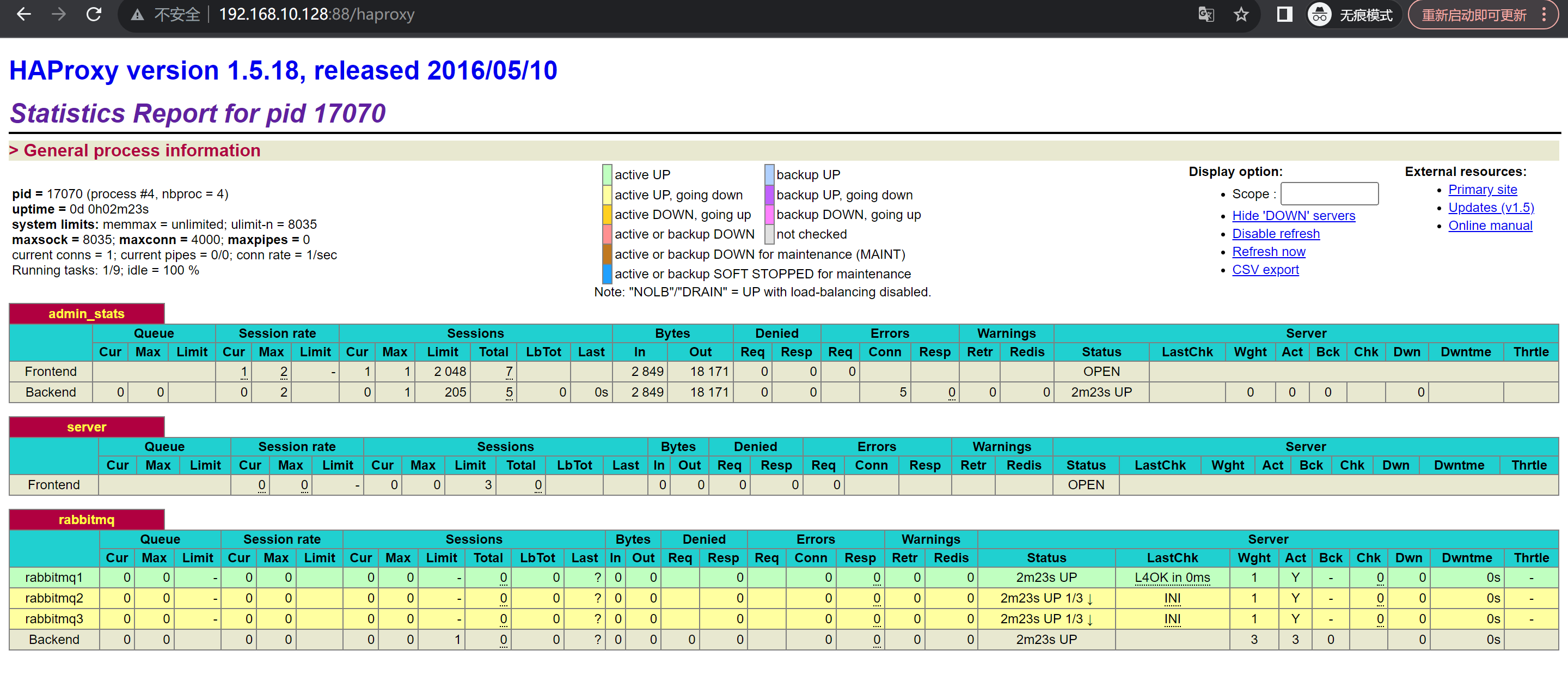
RabbitMQ集群配置以及负载均衡配置
RabbitMQ集群配置以及负载均衡配置 环境配置集群配置安装rabbitmq启动rabbitmq开启远程登录添加用户并且授权用户添加数据存放目录和日志存放目录查看端口拷⻉erlang.cookie将mq-2、mq-3作为内存节点加⼊mq-1节点集群中查看集群状态添加一个新的队列 RabbitMq负载均衡配置-HAPr…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
