P9836 种树
容易想到分解因数。
对于一个数 p p p 的因数个数,假设它可以被分解质因数成 a 1 i 1 a 2 i 2 a 3 i 3 ⋯ a k c k a_1^{i_1} a_2^{i_2} a_3^{i_3}\cdots a_k^{c_k} a1i1a2i2a3i3⋯akck 的形式,则其因数个数为 ( i 1 + 1 ) ( i 2 + 1 ) ( i 3 + 1 ) ⋯ ( i k + 1 ) (i_1+1)(i_2+1)(i_3+1)\cdots(i_k+1) (i1+1)(i2+1)(i3+1)⋯(ik+1)。
我们对序列 p p p 和 w w w 质因数分解之后再考虑这个问题。对于每次从 w w w 拆分出的一个质因子 A A A,我们假设一棵树 p i p_i pi,原来它的贡献为 x x x,对于该棵树高的质因数拆分中质因子 A A A 的出现次数为 t t t,则乘上该质因子之后它的贡献会变为 x ⋅ t + 2 t + 1 x\cdot \dfrac{t+2}{t+1} x⋅t+1t+2,容易证明分子越小即 t t t 越小对答案的贡献越大。
由于数据范围是 1 0 4 10^4 104,质因数的上界是很有限的。设 a ( i , j ) a(i,j) a(i,j) 表示 i j i^j ij 在所有树高的质因数拆分中出现了多少次,每一次取到的一个 w w w 的质因子 A A A,把它计算到当前存在且 k k k 最小的 A k A^k Ak 上即可。
注意筛 n n n 的质因数要筛到 n n n。
#include <bits/stdc++.h>
using namespace std;
#define int long longconst int maxn=1e4+5;
int a[maxn][30],ans=1,p[maxn],mod=998244353,n,w;void calc(int x)
{for(int i=2;i<=max(x,w);i++){int cnt=0;while(x%i==0) x/=i,cnt++;a[i][cnt]++;ans=ans*(cnt+1)%mod;// cout<<cnt<<endl;}
}signed main()
{cin>>n>>w;for(int i=1;i<=n;i++) cin>>p[i],calc(p[i]);// for(int i=1;i<=n;i++) cout<<a[i][1]<<endl;for(int A=2;A<=w;A++)while(w%A==0){int k=0;while(!a[A][k]) k++; ans/=(k+1),ans%=mod,ans*=(k+2),ans%=mod;w/=A,a[A][k]--,a[A][k+1]++;// cout<<w<<endl;} cout<<ans;return 0;
}
相关文章:

P9836 种树
容易想到分解因数。 对于一个数 p p p 的因数个数,假设它可以被分解质因数成 a 1 i 1 a 2 i 2 a 3 i 3 ⋯ a k c k a_1^{i_1} a_2^{i_2} a_3^{i_3}\cdots a_k^{c_k} a1i1a2i2a3i3⋯akck 的形式,则其因数个数为 ( i 1 1 ) ( i 2 1 )…...
C# 查询腾讯云直播流是否存在的API实现
应用场景 在云考试中,为防止作弊行为的发生,会在考生端部署音视频监控系统,当然还有考官方监控墙系统。在实际应用中,考生一方至少包括两路直播流: (1)前置摄像头:答题的设备要求使…...
JAVA开源项目 于道前端项目 启动步骤参考
1. 安装 启动过程有9个步骤: 1.1 安装 Node JS , V18版本的 (安装步骤省略) 1.2 安装 npm install -g yarn ,node JS里边好像自带npm ,通过npm的命令安装 yarn 1.3 切换到项目中去安装,npm install &a…...
深入理解ElasticSearch分片
1. 路由计算 当索引一个文档的时候,文档会被存储到一个主分片中。 Elasticsearch 如何知道一个文档应该存放到哪个分片中呢?当我们创建文档时,它如何决定这个文档应当被存储在分片 1 还是分片 2 中呢?首先这肯定不会是随机的&…...
【Python】AppUI自动化—appium自动化元素定位、元素事件操作(17)下
文章目录 前言一.Appium 元素定位1.定位方式种类2.如何定位2.1 id定位2.2 className定位2.3 content-desc 定位2.4 Android Uiautomator定位4.1 text定位4.2 text模糊定位4.3 text正则匹配定位4.4 resourceId定位4.5 resourceId正则匹配定位4.6 className定位4.7 className正则…...

SpringBoot使用MyBatis多数据源
SpringBoot使用MyBatis多数据源 我们以 Mybatis Xml和注解两种版本为例,给大家展示如何如何配置多数据源。 1、注解方式 数据库文件: DROP TABLE IF EXISTS users; CREATE TABLE users (id bigint(20) NOT NULL AUTO_INCREMENT COMMENT 主键id,userN…...
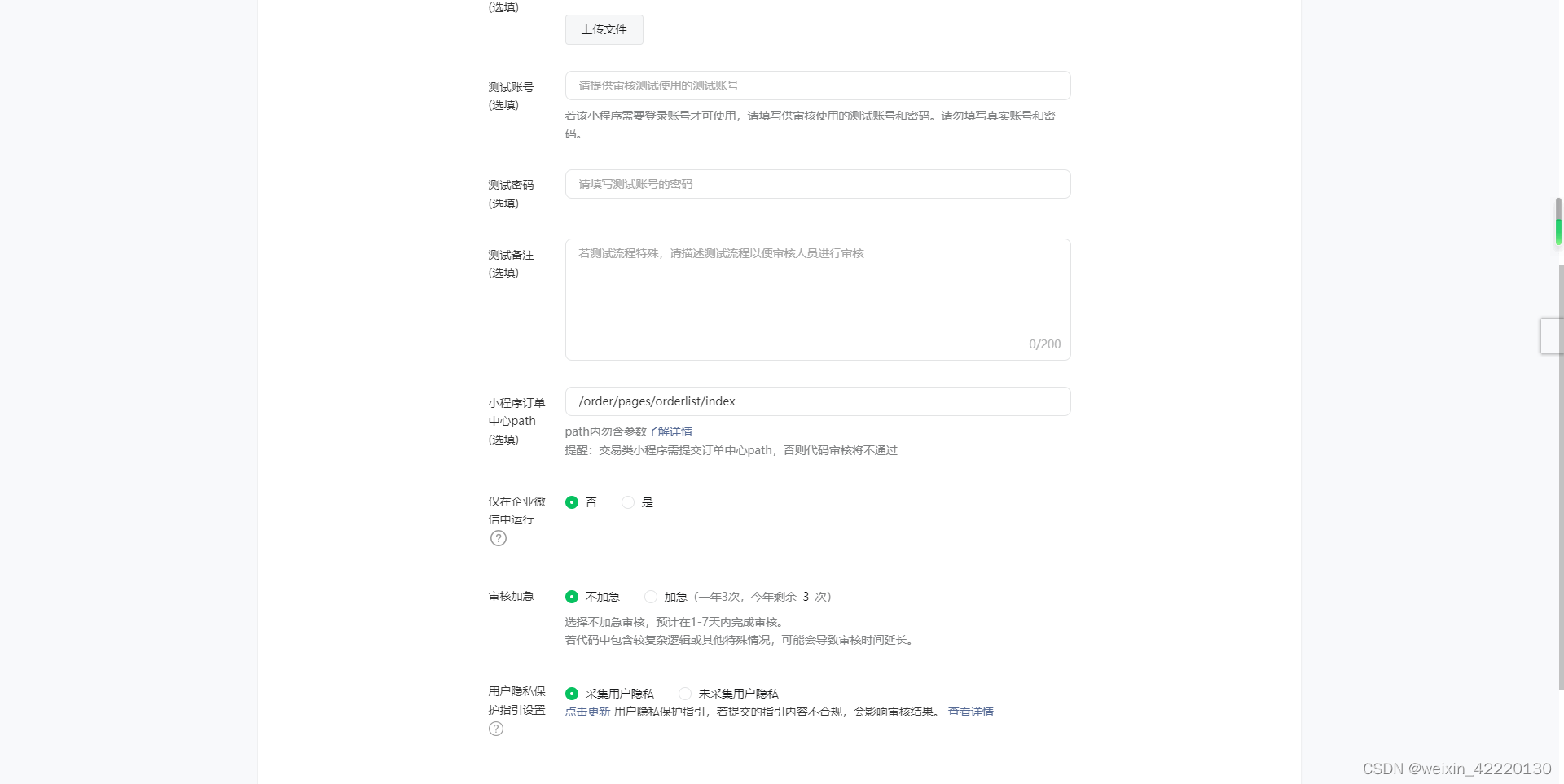
小程序版本审核未通过,需在开发者后台「版本管理—提交审核——小程序订单中心path」设置订单中心页path,请设置后再提交代码审核
小程序版本审核未通过,需在开发者后台「版本管理—提交审核——小程序订单中心path」设置订单中心页path,请设置后再提交代码审核 因小程序尚未发布,订单中心不能正常打开查看,请先发布小程序后再提交订单中心PATH申请 初次提交…...
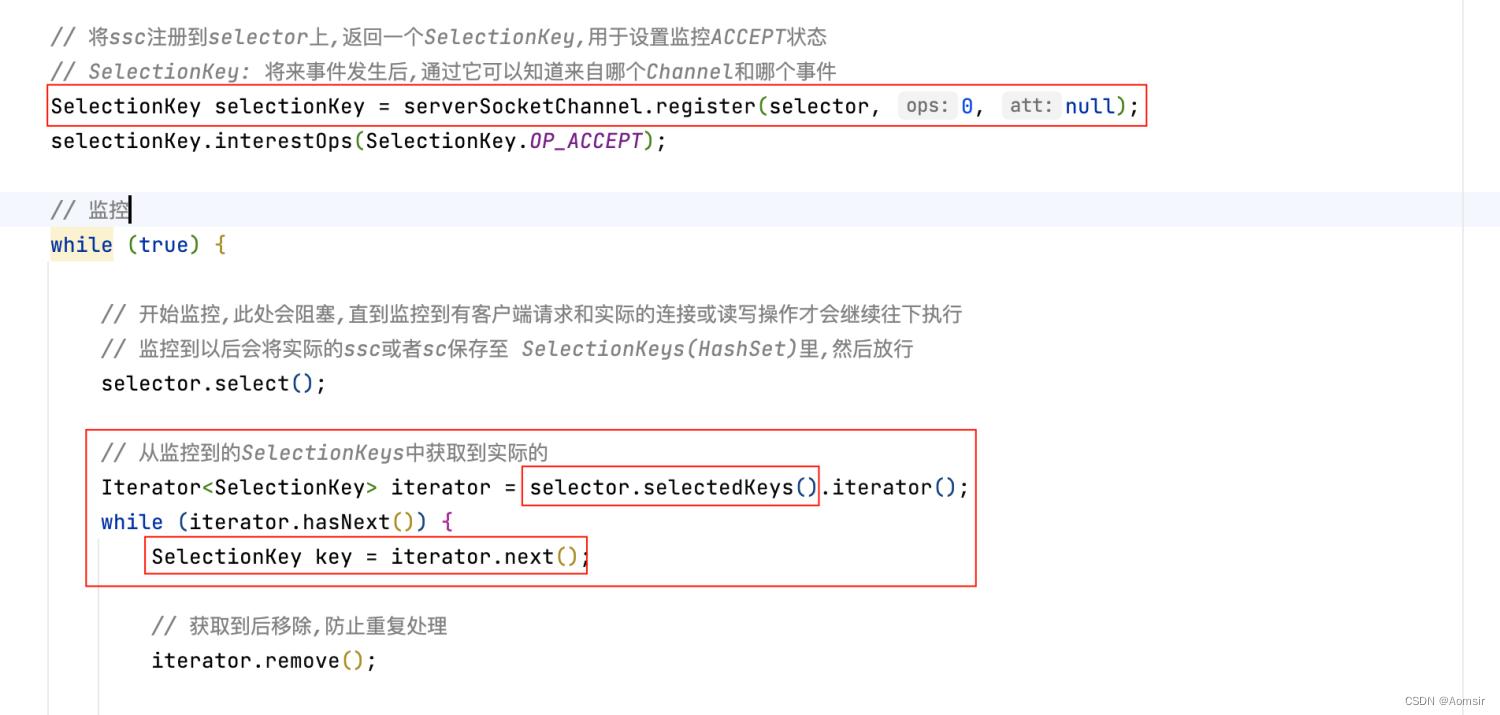
Netty入门指南之NIO Selector监管
作者简介:☕️大家好,我是Aomsir,一个爱折腾的开发者! 个人主页:Aomsir_Spring5应用专栏,Netty应用专栏,RPC应用专栏-CSDN博客 当前专栏:Netty应用专栏_Aomsir的博客-CSDN博客 文章目录 参考文献前言问题解…...

Spring Cloud学习(六)【统一网关 Gateway】
文章目录 网关的功能搭建网关服务路由断言工厂Route Predicate Factory路由过滤器 GatewayFilter过滤器执行顺序跨域问题处理 网关的功能 网关功能: 身份认证和权限校验服务路由、负载均衡请求限流 在SpringCloud中网关的实现包括两种: gatewayzuul …...

基于单片机的空调智能控制器的设计
**单片机设计介绍,基于单片机的空调智能控制器的设计 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于单片机的空调智能控制器需要具备输入输出端口、定时器、计数器等模块,以便对空调进行精确控制。下…...
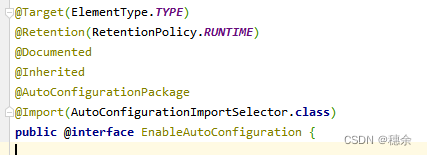
Spring Boot自动配置原理、实战、手撕自动装配源码
Spring Boot自动配置原理 相比较于传统的 Spring 应用,搭建一个 SpringBoot 应用,我们只需要引入一个注解 SpringBootApplication,就可以成功运行。 前面四个不用说,是定义一个注解所必须的,关键就在于后面三个注解&a…...

111111111111111
全局锁 就是对整个数据库进行加锁,加锁之后整个数据库就处于只读状态,后续的DML写语句,DDL语句,以及对更新事务的提交操作都会被阻塞,典型地使用场景就是做整个数据库的逻辑备份,对所有的表进行锁定&#x…...
React动态生成二维码和毫米(mm)单位转像素(px)单位
一、使用qrcode.react生成二维码,qrcode.react - npm 很简单,安装依赖包,然后引用就行了 npm install qrcode.react或者 yarn add qrcode.react直接上写好的代码 import React, {useEffect, useState} from react; import QRCode from qr…...
SpringMvc 常见面试题
1、SpringMvc概述 1.1、什么是Spring MVC ?简单介绍下你对springMVC的理解? Spring MVC是一个基于Java的实现了MVC设计模式的请求驱动类型的轻量级Web框架,通过把Model,View,Controller分离,将web层进行职责解耦&am…...
jmeter接口自动化测试工具在企业开展实际的操作
在企业使用jmeter开展实际的接口自动化测试工具,建议按如下操作流程, 可以使整个接口测试过程更规范,更有效。 接口自动化的流程: 1、获取到接口文档:swagger、word、excel ... 2、熟悉接口文档然后设计测试用例&am…...
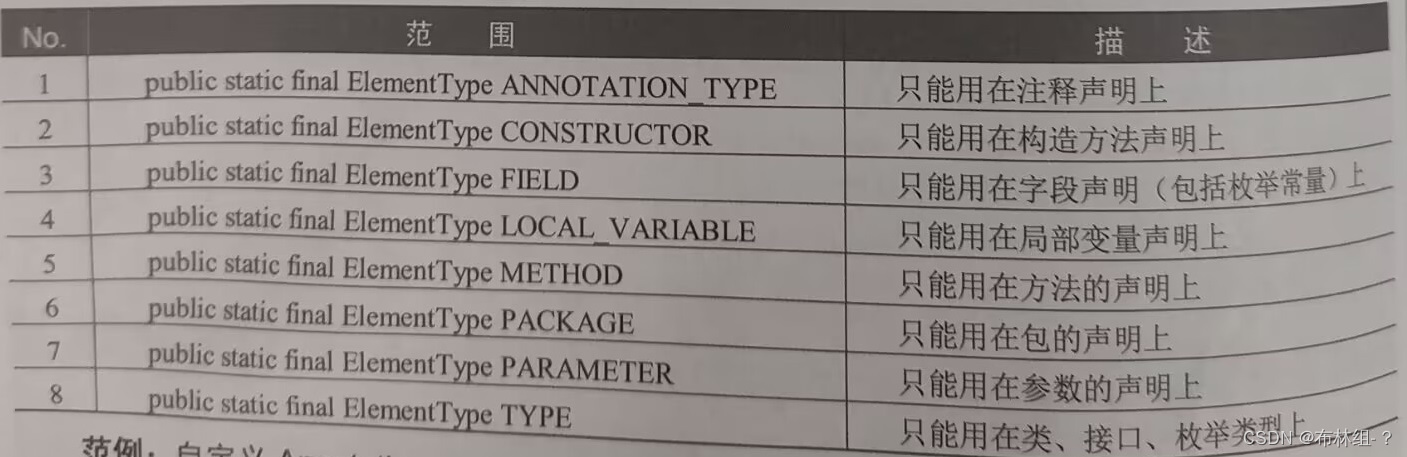
第17章 反射机制
通过本章需要理解反射机制操作的意义以及Class类的作用,掌握反射对象实例化操作,并且可以深刻理解反射机制与工厂模式结合意义。掌握类结构反射操作的实现,并且可以通过反射实现类中构造方法、普通方法、成员属性的操作。掌握反射机制与简单J…...
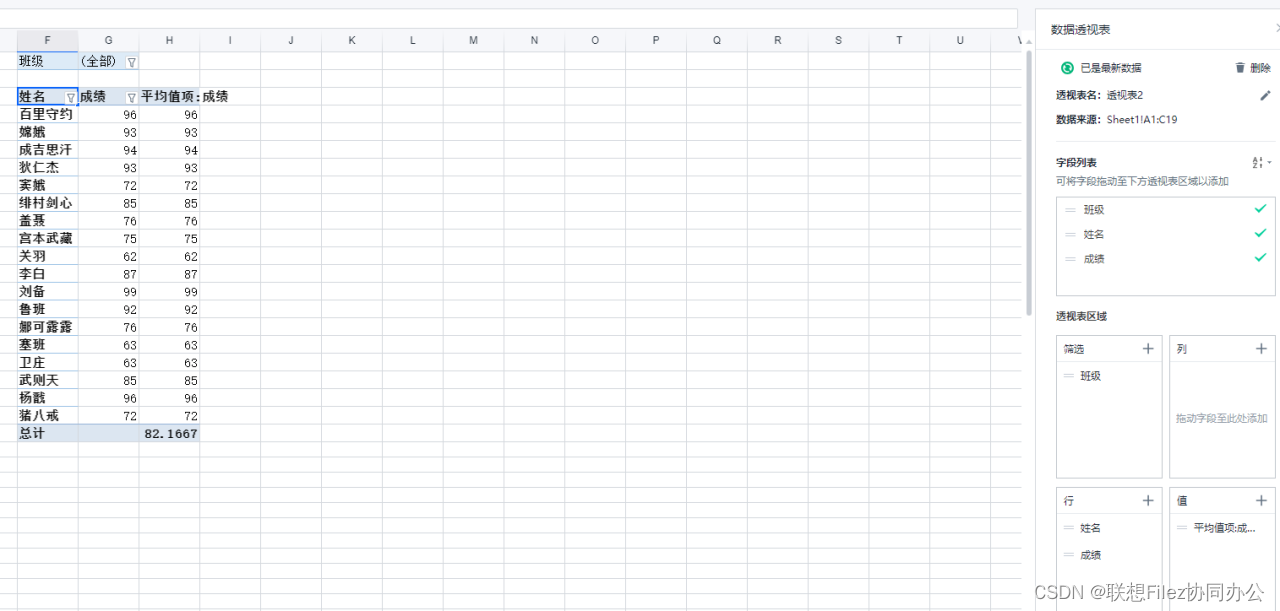
如何在在线Excel文档中对数据进行统计
本次我们将用zOffice表格的公式与数据透视表分析样例(三个班级的学生成绩)。zOffice表格内置了大量和Excel相同的统计公式,可以进行各种常见的统计分析,如平均值、标准差、相关性等。同时,zOffice也有数据透视表功能&a…...
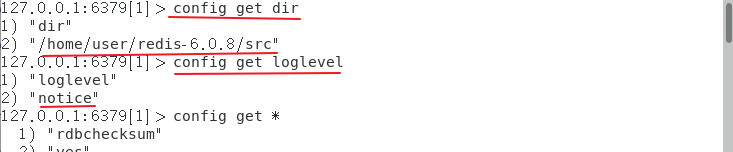
redis配置文件详解
一、配置文件位置 以配置文件启动 Redis 的配置文件位于 Redis 安装目录下,文件名为 redis.conf ( Windows名为redis.windows. conf) 例: # 这里要改成你自己的安装目录 cd ./redis-6.0.8 vim redis.conf redis对配置文件对大小写不敏感 二、配置文件 1、获取当前服务的…...

前端设计模式之【工厂模式】
文章目录 前言什么时候不用介绍工厂模式的流程例子优点缺陷后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:前端设计模式 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板。…...
Python与ArcGIS系列(一)ArcGIS中使用Python
目录 0 简述1 arcgis中的python窗口2 开始编写代码 0 简述 按照惯例,作为本系列专栏的第一篇,先简单地介绍下本系列文章的内容:通过python语言创建arcgis环境脚本、将脚本以工具箱形式存放在arcgis中、通过脚本自动执行地理处理、数据修复、…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
