【算法】牛的旅行（图的直径，floyd算法求最短路）

题目

        农民John的农场里有很多牧区，有的路径连接一些特定的牧区。

        一片所有连通的牧区称为一个牧场。

        但是就目前而言，你能看到至少有两个牧区不连通。

        现在，John想在农场里添加一条路径（注意，恰好一条）。

        一个牧场的直径就是牧场中最远的两个牧区的距离（本题中所提到的所有距离指的都是最短的距离）。

        考虑如下的两个牧场，每一个牧区都有自己的坐标：

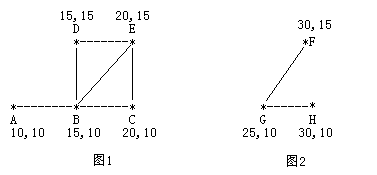
        图 1 是有 5 个牧区的牧场，牧区用“*”表示，路径用直线表示。

        图 1 所示的牧场的直径大约是 12.07106, 最远的两个牧区是 A 和 E，它们之间的最短路径是 A-B-E。

        图 2 是另一个牧场。

        这两个牧场都在John的农场上。

        John将会在两个牧场中各选一个牧区，然后用一条路径连起来，使得连通后这个新的更大的牧场有最小的直径。

        注意，如果两条路径中途相交，我们不认为它们是连通的。

        只有两条路径在同一个牧区相交，我们才认为它们是连通的。

        现在请你编程找出一条连接两个不同牧场的路径，使得连上这条路径后，所有牧场（生成的新牧场和原有牧场）中直径最大的牧场的直径尽可能小。

        输出这个直径最小可能值。

输入格式

        第 1 行：一个整数 N, 表示牧区数；

        第 2 到 N+1 行：每行两个整数 X,Y， 表示 N 个牧区的坐标。每个牧区的坐标都是不一样的。

        第 N+2 行到第 2*N+1 行：每行包括 N 个数字 ( 0或1 ) 表示一个对称邻接矩阵。

        例如，题目描述中的两个牧场的矩阵描述如下：

样例：A B C D E F G H 
A 0 1 0 0 0 0 0 0 
B 1 0 1 1 1 0 0 0 
C 0 1 0 0 1 0 0 0 
D 0 1 0 0 1 0 0 0 
E 0 1 1 1 0 0 0 0 
F 0 0 0 0 0 0 1 0 
G 0 0 0 0 0 1 0 1 
H 0 0 0 0 0 0 1 0

        输入数据中至少包括两个不连通的牧区。

输出格式

        只有一行，包括一个实数，表示所求答案。

        数字保留六位小数。

数据范围

        1 ≤ N ≤ 150
        0≤ X , Y ≤ 10^5

思路

        1、先将数据存储起来

        2、初始化点到点的距离

        3、使用floyd算法算出点到点的最小距离

        4、保留所有点到点 i 的最大距离，储存到maxd[]数组中。

        5、遍历maxd[]数组，距离最大的值就是所有连通图直径中的最大值，使用res1储存。

        6、遍历所有点到点的距离，如果距离大于或等于INF则表明这两个点不在同一个连通图内，将这两个点连接起来，得到的直径为maxd[ i ] + maxd[ j ] + get_dist(q[ i ],q[ j ]);如果小于res2则更新res2。

        7、输出res1与res2中的最小值。

代码

#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;typedef pair<int,int> PII;const int N = 150;
const double INF = 1e20;int n;// n代表牧区数目
PII q[N];// 用来储存牧区的坐标
char g[N][N];// 用来储存邻接矩阵（g[i][j] == '1' 代表点i到点j是连通的，否则代表不连通）
double d[N][N],maxd[N];// d[i][j]代表点i到点j的最小距离，maxd[i]代表所有能到达点i的最小距离中的最大距离double get_dist(PII a,PII b)//求点a到点b的距离
{double dx = a.x - b.x, dy = a.y - b.y;return sqrt(dx * dx + dy * dy);
}int main()
{cin >> n;// 输入牧区数量for(int i = 0; i < n; i ++) cin >> q[i].x >> q[i].y;// 依次输入牧区坐标for(int i = 0; i < n; i ++) cin >> g[i];// 输入邻接矩阵for(int i = 0; i < n; i ++)for(int j = 0; j < n; j ++)if(i != j){if(g[i][j] == '1') d[i][j] = get_dist(q[i],q[j]);// 初始化点i到点j的距离else d[i][j] = INF;}for(int k = 0; k < n; k ++)for(int i = 0; i < n; i ++)for(int j = 0; j < n; j ++)d[i][j] = min(d[i][j],d[i][k] + d[k][j]);// 使用floyd算法求多源汇最短路（任意点到任意点的最短距离）for(int i = 0; i < n; i ++)for(int j = 0; j < n; j ++)if(d[i][j] < INF)maxd[i] = max(maxd[i],d[i][j]);// 求出所有能到达点i的最小距离中的最大距离double res1 = 0;for(int i = 0; i < n; i ++) res1 = max(res1,maxd[i]);// 使用res1储存所有连通图中直径的最大的值double res2 = INF;for(int i = 0; i < n; i ++)for(int j = 0; j < n; j ++)if(d[i][j] >= INF)res2 = min(res2,get_dist(q[i],q[j]) + maxd[i] + maxd[j]);// 使用res2储存连接一条边之后所得到新的连通图的直径的最小值printf("%lf\n",max(res1,res2));return 0;}

题目来自网站：https://www.acwing.com/