GBDT减少模型偏差、随机森林减小模型方差
1、Adaboost算法原理,优缺点:
理论上任何学习器都可以用于Adaboost.但一般来说,使用最广泛的Adaboost弱学习器是决策树和神经网络。对于决策树,Adaboost分类用了CART分类树,而Adaboost回归用了CART回归树。
Adaboost算法可以简述为三个步骤:
(1)首先,是初始化训练数据的权值分布D1。假设有N个训练样本数据,则每一个训练样本最开始时,都被赋予相同的权值:w1=1/N。
(2)然后,训练弱分类器hi。具体训练过程中是:如果某个训练样本点,被弱分类器hi准确地分类,那么在构造下一个训练集中,它对应的权值要减小;相反,如果某个训练样本点被错误分类,那么它的权值就应该增大。权值更新过的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
(3)最后,将各个训练得到的弱分类器组合成一个强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。
换而言之,误差率低的弱分类器在最终分类器中占的权重较大,否则较小。
Adaboost的主要优点有:
1)Adaboost作为分类器时,分类精度很高。
2)在Adaboost的框架下,可以使用各种回归分类模型来构建弱学习器,不用对特征进行筛选,非常灵活。
3)作为简单的二元分类器时,构造简单,结果可理解。
4)不容易发生过拟合。
Adaboost的主要缺点有:
1)对异常样本敏感,异常样本在迭代中可能会获得较高的权重,影响最终的强学习器的预测准确性。
算法推导见笔记。
2、GBDT算法原理
GBDT在BAT大厂中也有广泛的应用,假如要选择3个最重要的机器学习算法的话,个人认为GBDT应该占一席之地。
基本思想:积跬步以至千里,每次学习一点。先用一个初始值来学习一棵决策树,叶子处可以得到预测的值,以及预测之后的残差,然后后面的决策树就是要基于前面决策树的残差来学习,直到预测值和真实值的残差为0。最后对于测试样本的预测值,就是前面许多棵决策树预测值的累加。
GBDT的思想可以用一个通俗的例子解释,假如有个人30岁,我们首先用20岁去拟合,发现损失有10岁,这时我们用6岁去拟合剩下的损失,发现差距还有4岁,第三轮我们用3岁拟合剩下的差距,差距就只有一岁了。如果我们的迭代轮数还没有完,可以继续迭代下面,每一轮迭代,拟合的岁数误差都会减小。
GBDT也是迭代,使用了前向分布算法,但是弱学习器限定了只能使用CART回归树模型.(GBDT的会累加所有树的结果,而这种累加是无法通过分类完成的,因此GBDT的树都是CART回归树,而不是分类树(尽管GBDT调整后也可以用于分类但不代表GBDT的树为分类树))
它的每一次计算都是为了减少上一次的残差,而为了消除残差,我们可以在残差减小的梯度方向上建立模型,所以说,在GradientBoost中,每个新的模型的建立是为了使得之前的模型的残差往梯度下降的方法,与传统的Boosting中关注正确错误的样本加权有着很大的区别。
GBDT通过多轮迭代,每轮迭代产生一个弱分类器,每个分类器在上一轮分类器的残差基础上进行训练。对弱分类器的要求一般是足够简单,并且是低方差和高偏差的。因为训练的过程是通过降低偏差来不断提高最终分类器的精度。
通过损失函数的负梯度来拟合,我们找到了一种通用的拟合损失误差的办法,这样无轮是分类问题还是回归问题,我们通过其损失函数的负梯度的拟合,就可以用GBDT来解决我们的分类回归问题。区别仅仅在于损失函数不同导致的负梯度不同而已。
3、GBDT算法步骤
损失函数主要有:指数损失、对数损失、均方差、绝对损失
让损失函数沿着梯度方向的下降。这个就是gbdt 的 gb的核心了。 利用损失函数的负梯度在当前模型的值作为回归问题提升树算法中的残差的近似值去拟合一个回归树。gbdt 每轮迭代的时候,都去拟合损失函数在当前模型下的负梯度。
由于上述高偏差和简单的要求,每个分类回归树的深度不会很深。最终的总分类器 是将每轮训练得到的弱分类器加权求和得到的(也就是加法模型)。
对于回归问题:
对于分类问题:样本输出不是连续的值,而是离散的类别,导致我们无法直接从输出类别去拟合类别输出的误差。
主要有两个方法:一个是用指数损失函数,此时GBDT退化为Adaboost算法。另一种方法是用类似于逻辑回归的对数似然损失函数的方法。也就是说,我们用的是类别的预测概率值和真实概率值的差来拟合损失。
4、gbdt 如何构建特征
gbdt 本身是不能产生特征的,但是我们可以利用gbdt去产生特征的组合。利用gbdt去产生特征的组合,再采用逻辑回归进行处理,增强逻辑回归对非线性分布的拟合能力。
我们使用 GBDT 生成了两棵树,两颗树一共有五个叶子节点。我们将样本 X 输入到两颗树当中去,样本X 落在了第一棵树的第二个叶子节点,第二颗树的第一个叶子节点,于是我们便可以依次构建一个五纬的特征向量,每一个纬度代表了一个叶子节点,样本落在这个叶子节点上面的话那么值为1,没有落在该叶子节点的话,那么值为 0。于是对于该样本,我们可以得到一个向量[0,1,0,1,0] 作为该样本的组合特征,和原来的特征一起输入到逻辑回归当中进行训练。实验证明这样会得到比较显著的效果提升。
补充:
GBDT选择特征的细节其实是想问你CART Tree生成的过程。CART TREE 生成的过程其实就是一个选择特征的过程。
选择特征是:遍历每个特征和每个特征的所有切分点,找到最优的特征和最优的切分点。多个CART TREE 生成过程中,选择最优特征切分较多的特征就是重要的特征。
5、GBDT 如何用于分类 ?
参考:https://www.cnblogs.com/ModifyRong/p/7744987.html
gbdt 无论用于分类还是回归一直都是使用的CART 回归树。这里面的核心是因为gbdt 每轮的训练是在上一轮的训练的残差基础之上进行训练的。这里的残差就是当前模型的负梯度值 。这个要求每轮迭代的时候,弱分类器的输出的结果相减是有意义的。残差相减是有意义的,类别相减是没有意义的。
方法流程:
(1)我们在训练的时候,是针对样本 X 每个可能的类都训练一个分类回归树。举例说明,目前样本有三类,也就是 K = 3。样本 x 属于 第二类。那么针对该样本 x 的分类结果,其实我们可以用一个 三维向量 [0,1,0] 来表示。0表示样本不属于该类,1表示样本属于该类。由于样本已经属于第二类了,所以第二类对应的向量维度为1,其他位置为0。
针对样本有 三类的情况,我们实质上是在每轮的训练的时候是同时训练三颗树。第一颗树针对样本x的第一类,输入为(x,0)。第二颗树输入针对 样本x 的第二类,输入为(x,1)。第三颗树针对样本x 的第三类,输入为(x,0)。
在这里每颗树的训练过程其实就是就是我们之前已经提到过的CATR TREE 的生成过程。在此处我们参照之前的生成树的程序 即可以就解出三颗树,以及三颗树对x 类别的预测值f1(x),f2(x),f3(x)。那么在此类训练中,我们仿照多分类的逻辑回归 ,使用softmax 来产生概率,则属于类别 1 的概率。
这样我们可以遍历所有特征的所有特征值,找到让均方损失最小的特征以及其对应的特征值。生成三颗树后,对于测试样本预测概率。
6、优缺点:
目前GBDT的算法比较好的库是xgboost。当然scikit-learn也可以。
GBDT主要的优点有:
-
可以灵活处理各种类型的数据,包括连续值和离散值,处理分类和回归问题。
-
在相对少的调参时间情况下,预测的准备率也可以比较高。这个是相对SVM来说的。
-
可以用于筛选特征。
4)使用一些健壮的损失函数,对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。
GBDT的主要缺点有:
1)由于弱学习器之间存在依赖关系,难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。
7、GBDT和随机森林对比
相同点:
1.都是由多棵树组成;
2.最终的结果都是由多棵树一起决定;
不同点:
(1)随机森林的子树可以是分类或回归树,而GBDT只能是回归树;
(2)基于bagging思想,而gbdt是boosting思想,即采样方式不同
(3)随机森林可以并行生成,而GBDT只能是串行;
(4)输出结果,随机森林采用多数投票,GBDT将所有结果累加起来;
(5)随机森林对异常值不敏感,GBDT敏感,随进森林减少方差,GBDT减少偏差;
8、GBDT和随机森林哪个容易过拟合?
随机森林,因为随机森林的决策树尝试拟合数据集,有潜在的过拟合风险,而boosting的GBDT的决策树则是拟合数据集的残差,然后更新残差,由新的决策树再去拟合新的残差,虽然慢,但是难以过拟合。
相关文章:

GBDT减少模型偏差、随机森林减小模型方差
1、Adaboost算法原理,优缺点: 理论上任何学习器都可以用于Adaboost.但一般来说,使用最广泛的Adaboost弱学习器是决策树和神经网络。对于决策树,Adaboost分类用了CART分类树,而Adaboost回归用了CART回归树。 Adaboost…...

使用IDEA工具处理git合并后的冲突的细节
使用 IDEA 处理合并(merge) 使用IDEA处理git合并如果遇到冲突,对冲突文件的不冲突部分需要处理吗?会自动将双方不冲突的部分合并吗? 比如如下,使用 IDEA 合并 branch1 到 branch2 分支,出现了冲突,如下图…...

快速下载ChatGLM系列模型
1. 说明与步骤 在无法访问huggingface的网络环境下(或者是网速不够好时),(目前)还可以使用参考1中清华云盘的链接来下载,在linux下可以直接用如下wget命令来下载最耗时的模型部分。注意还需要把模型的.py等…...
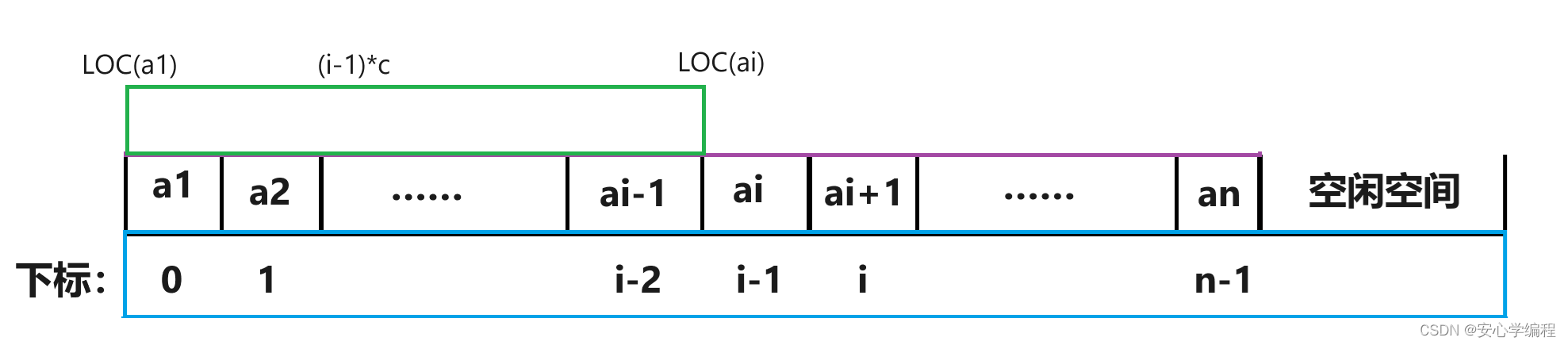
【数据结构】顺序表 | 详细讲解
在计算机中主要有两种基本的存储结构用于存放线性表:顺序存储结构和链式存储结构。本篇文章介绍采用顺序存储的结构实现线性表的存储。 顺序存储定义 线性表的顺序存储结构,指的是一段地址连续的存储单元依次存储链性表的数据元素。 线性表的…...
——第1天:什么是风控建模?)
100天精通风控建模(原理+Python实现)——第1天:什么是风控建模?
风控模型已在各大银行和公司都实际运用于业务,用于营销和风险控制等。本文以视频的形式阐述什么是风控建模,并提供风控建模原理和Python实现文章清单。首先了解什么是风控建模? 下文梳理风控模型搭建的原理和Python实现,按顺序做成清单的形式,点击即可进入相应文章链接。方…...

HTML转义字符
HTML,XML文件中存在部分字符作为标志字符无法作为文本内容使用,如< >,如果想在文本中输出,可使用转义字符。 < 的转义字符为 " < " > 的转义字符为 " > " <TextView.... ....android:t…...

【STM32】
STM32 1 CMSIS1.1 概述1.2 CMSIS 应用程序文件描述 2 库2.1 简介2.2 标准外设库(standrd Peripheral Libraries)2.3 HAL 库2.3.1 目录结构2.3.2 HAL库API函数和变量的命名规则2.3.3 HAL库对寄存器位操作的相关宏定义2.3.4 HAL库回调函数2.3.5 HAL使用注意…...
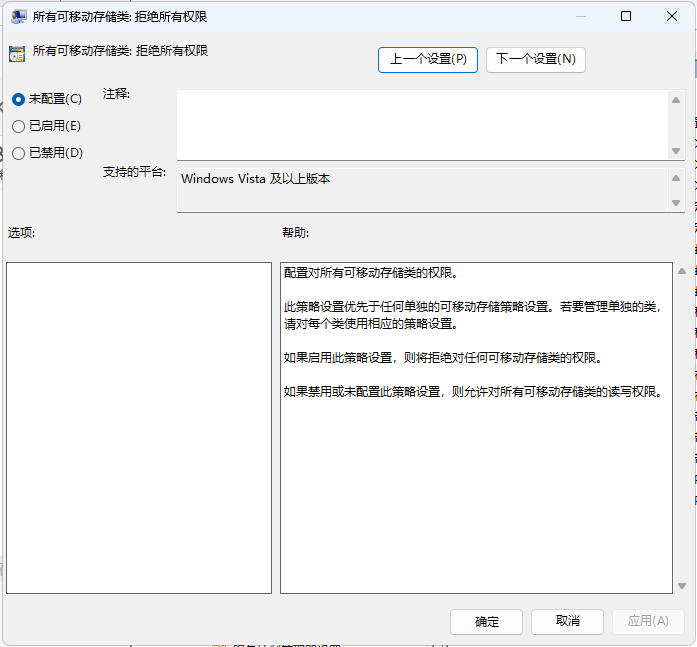
U盘不可以访问的维护
u盘打不开,可按下图,设置:winR→gpedit.msc;配置“管理模板”→“系统”→“可移动存储访问”→“所有可移动存储类”。 然后,选择“未配置”,如下图...
SpringCloud 微服务全栈体系(十三)
第十一章 分布式搜索引擎 elasticsearch 二、索引库操作 索引库就类似数据库表,mapping 映射就类似表的结构。 我们要向 es 中存储数据,必须先创建“库”和“表”。 1. mapping 映射属性 mapping 是对索引库中文档的约束,常见的 mapping …...

ROC 曲线详解
前言 ROC 曲线是一种坐标图式的分析工具,是由二战中的电子和雷达工程师发明的,发明之初是用来侦测敌军飞机、船舰,后来被应用于医学、生物学、犯罪心理学。 如今,ROC 曲线已经被广泛应用于机器学习领域的模型评估,说…...

113.路径总和II
原题链接:113.路径总和II 需复刷 思路: 跟112.路径总和不同,该题是要你找出所有相同的路径,那么此时就要注意存储,递归和回溯了。 全代码: class Solution { public:vector<vector<int>> re…...

【Linux】WSL安装Kali及基本操作
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍WSL安装Kali及基本操作。 学其所用,用其所学。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下次更新不迷路…...
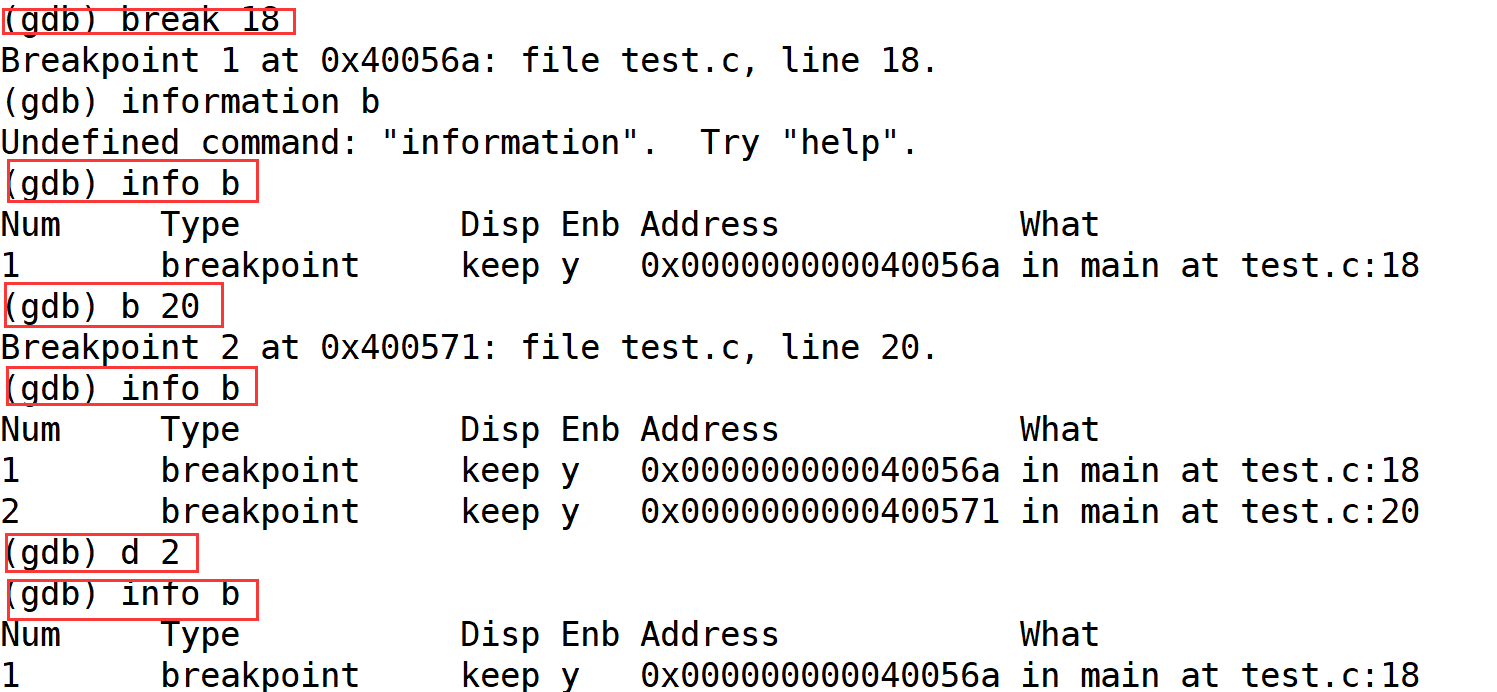
Linux基础开发工具之调试器gdb
文章目录 1.编译成的可调试的debug版本1.1gcc test.c -o testdebug -g1.2readelf -S testdebug | grep -i debug 2.调试指令2.0quit退出2.1list/l/l 数字: 显示代码2.2run/r运行2.3断点相关1. break num/b num: 设置2. info b: 查看3. d index: 删除4. n: F10逐过程5. p 变量名…...
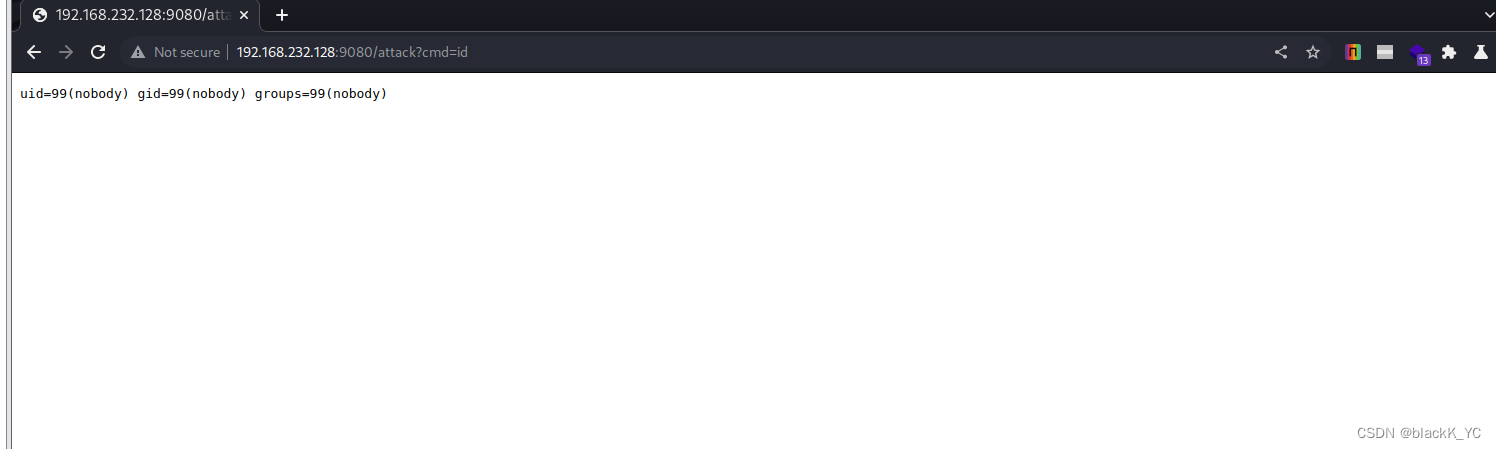
Apache APISIX 的 Admin API 默认访问令牌漏洞(CVE-2020-13945)漏洞复现
漏洞描述 Apache APISIX 是一个动态、实时、高性能的 API 网关。Apache APISIX 有一个默认的内置 API 令牌,可用于访问所有 admin API,通过 2.x 版本中添加的参数导致远程执行 LUA 代码。 漏洞环境及利用 启动docker环境 访问9080端口 通过 admin api…...
Clickhouse学习笔记(3)—— Clickhouse表引擎
前言: 有关Clickhouse的前置知识详见: 1.ClickHouse的安装启动_clickhouse后台启动_THE WHY的博客-CSDN博客 2.ClickHouse目录结构_clickhouse 目录结构-CSDN博客 Cickhouse创建表时必须指定表引擎 表引擎(即表的类型)决定了&…...

WebSocket是什么以及其与HTTP的区别
新钛云服已累计为您分享774篇技术干货 HTTP协议 HTTP是单向的,客户端发送请求,服务器发送响应。举个例子,当用户向服务器发送请求时,该请求采用HTTP或HTTPS的形式,在接收到请求后,服务器将响应发送给客户端…...

Flutter 实战:构建跨平台应用
文章目录 一、简介二、开发环境搭建三、实战案例:开发一个简单的天气应用1. 项目创建2. 界面设计3. 数据获取4. 实现数据获取和处理5. 界面展示6. 添加动态效果和交互7. 添加网络错误处理8. 添加刷新功能9. 添加定位功能10. 添加通知功能11. 添加数据持久化功能 《F…...

Python中68个内置函数的使用与归类
前言 在Python解释器中内置的、可以直接使用的函数。这些函数不需要额外的导入或安装,可以直接在Python代码中调用。Python内置函数包括了很多常用的功能,比如对数据类型的操作、数学运算、字符串处理、文件操作等。一些常见的内置函数包括print()、len…...

AGV無人搬送車控制系统Pytorn
import tkinter as tk import Main import monitoring # メインウィンドウを作成 root tk.Tk() root.title("AGV無人搬送車控制系统 ver1.0.0") # ウィンドウサイズを固定 root.geometry("501x340") root.resizable(False, False) # サイズ変更を…...
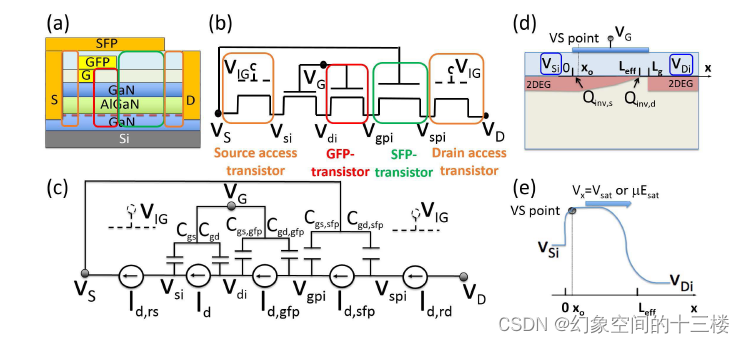
使用MVS-GaN HEMT紧凑模型促进基于GaN的射频和高电压电路设计
标题:Facilitation of GaN-Based RF- and HV-Circuit Designs Using MVS-GaN HEMT Compact Model 来源:IEEE TRANSACTIONS ON ELECTRON DEVICES(19年) 摘要—本文阐述了基于物理的紧凑器件模型在研究器件行为细微差异对电路和系统…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...
