ROC 曲线详解
前言
ROC 曲线是一种坐标图式的分析工具,是由二战中的电子和雷达工程师发明的,发明之初是用来侦测敌军飞机、船舰,后来被应用于医学、生物学、犯罪心理学。
如今,ROC 曲线已经被广泛应用于机器学习领域的模型评估,说到这里就不得不提到 Tom Fawcett 大佬,他一直在致力于推广 ROC 在机器学习领域的应用,他发布的论文《An introduction to ROC analysis》[1]更是被奉为 ROC 的经典之作(引用 2.2w 次),知名机器学习库 scikit-learn 中的 ROC 算法就是参考此论文实现,可见其影响力!
不知道大多数人是否和我一样,对于 ROC 曲线的理解只停留在调用 scikit-learn 库的函数,对于它的背后原理和公式所知甚少。
前几天我重读了《An introduction to ROC analysis》终于将 ROC 曲线彻底搞清楚了,独乐乐不如众乐乐!如果你也对 ROC 的算法及实现感兴趣,不妨花些时间看完全文,相信你一定会有所收获!
一、什么是 ROC 曲线
下图中的蓝色曲线就是 ROC 曲线,它常被用来评价二值分类器的优劣,即评估模型预测的准确度。
二值分类器,就是字面意思它会将数据分成两个类别(正/负样本)。例如:预测银行用户是否会违约、内容分为违规和不违规,以及广告过滤、图片分类等场景。篇幅关系这里不做多分类 ROC 的讲解。
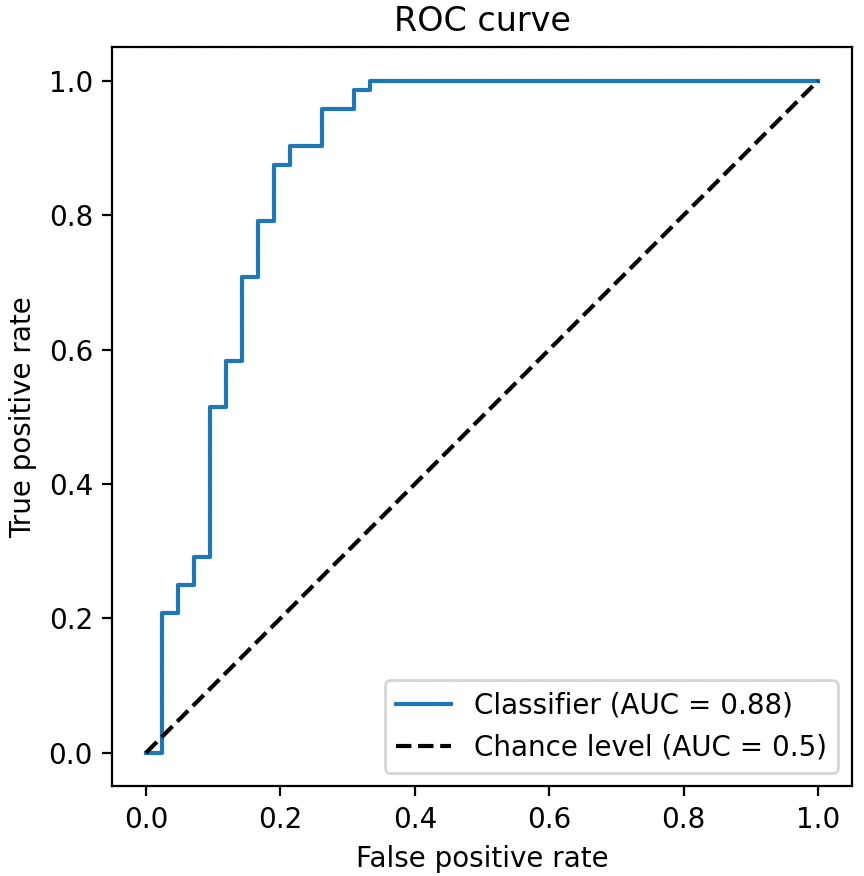
坐标系中纵轴为 TPR(真阳率/命中率/召回率)最大值为 1,横轴为 FPR(假阳率/误判率)最大值为 1,虚线为基准线(最低标准),蓝色的曲线就是 ROC 曲线。其中 ROC 曲线距离基准线越远,则说明该模型的预测效果越好。(TPR: True positive rate; FPR: False positive rate)
-
ROC 曲线接近左上角:模型预测准确率很高
-
ROC 曲线略高于基准线:模型预测准确率一般
-
ROC 低于基准线:模型未达到最低标准,无法使用
二、背景知识
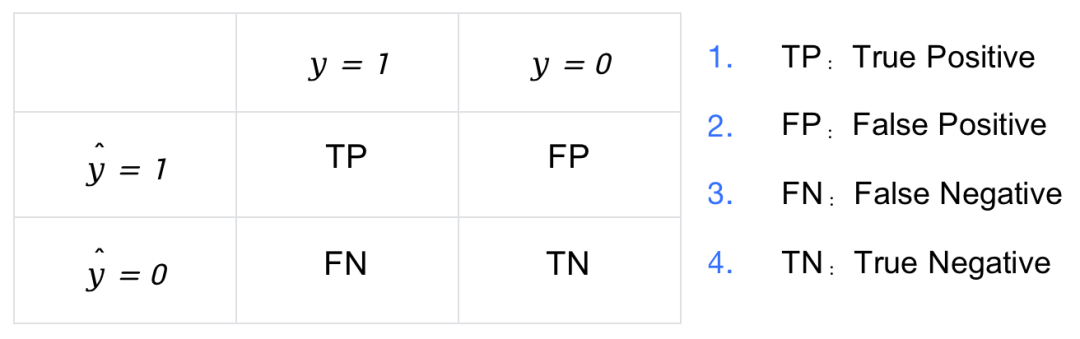
考虑一个二分类模型, 负样本(Negative) 为 0,正样本(Positive) 为 1。即:
-
标签
的取值为 0 或 1。
-
模型预测的标签为
,取值也是 0 或 1。
因此,将 与
两两组合就会得到 4 种可能性,分别称为:
2.1 公式
ROC 曲线的横坐标为 FPR(False Positive Rate),纵坐标为 TPR(True Positive Rate)。FPR 统计了所有负样本中 预测错误(FP) 的比例,TPR 统计了所有正样本中 预测正确(TP) 的比例,其计算公式如下,其中 # 表示统计个数,例如 #N 表示负样本的个数,#P 表示正样本的个数
2.2 计算方法
下面举一个实际例子作为讲解,以下表 5 个样本为例,讲解如何计算 FPR 和 TPR。
| id | 真实标签 | 预测标签 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 0 |
| 3 | 0 | 0 |
| 4 | 1 | 1 |
| 5 | 0 | 1 |
正样本数 ,负样本数
。
其中 且
的样本有 1 个,即
,所以
其中 且
的样本有 2 个,即
,所以
FPR 和 TPR 的取值范围均是 0 到 1 之间。对于 FPR,我们希望其越小越好。而对于 TPR,我们希望其越大越好。
至此,我们已经介绍完如何计算 FPR 和 TPR 的值,下面将会讲解如何绘制 ROC 曲线。
三、绘制 ROC 曲线
讲到这里,可能有的同学会问:ROC 不是一条曲线吗?讲了这么多它到底应该怎么画呢?下面将分为两部分讲解如何绘制 ROC 曲线,直接打通你的“任督二脉”彻底拿下 ROC 曲线:
-
第一部分:通过手绘的方式讲解原理
-
第二部分:Python 代码实现,代码清爽易读
3.1 手绘 ROC 曲线
一般在二分类模型里(标签取值为 0 或 1),会默认设定一个阈值 (threshold)。当预测分数大于这个阈值时,输出 1,反之输出 0。我们可以通过调节这个阈值,改变模型预测的输出,进而画出 ROC 曲线。
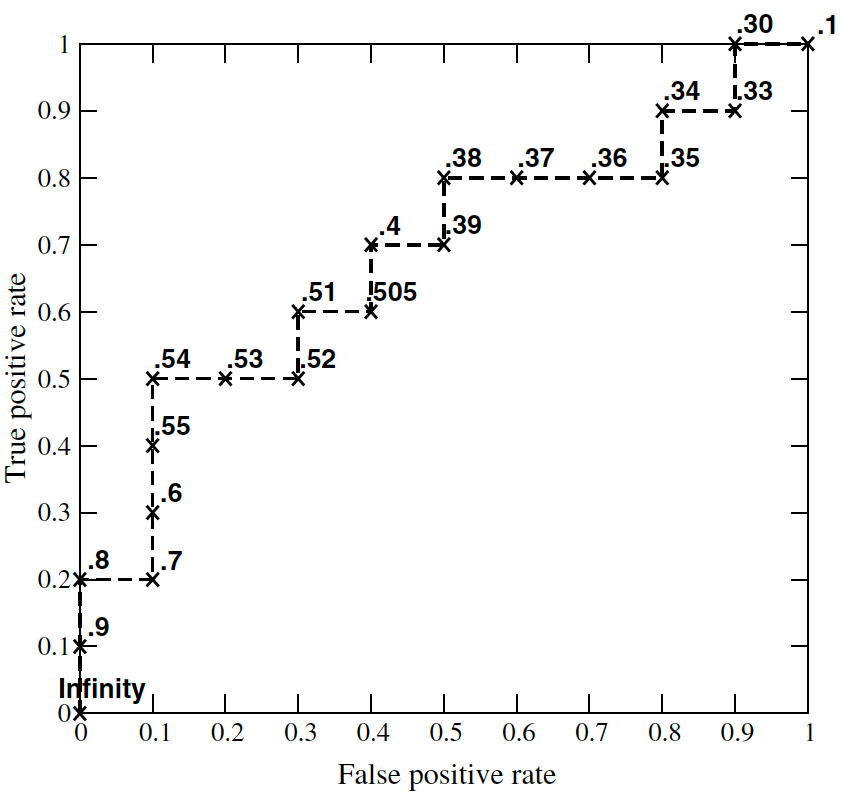
以下面表格中的 20 个点为例,介绍如何人工画出 ROC 曲线,其中正样本和负样本都是 10 个,即 。
| id | 真实标签 | 预测分数 | id | 真实标签 | 预测分数 |
|---|---|---|---|---|---|
| 1 | 1 | .9 | 11 | 1 | .4 |
| 2 | 1 | .8 | 12 | 0 | .39 |
| 3 | 0 | .7 | 13 | 1 | .38 |
| 4 | 1 | .6 | 14 | 0 | .37 |
| 5 | 1 | .55 | 15 | 0 | .36 |
| 6 | 1 | .54 | 16 | 0 | .35 |
| 7 | 0 | .53 | 17 | 1 | .34 |
| 8 | 0 | .52 | 18 | 0 | .33 |
| 9 | 1 | .51 | 19 | 1 | .30 |
| 10 | 0 | .505 | 20 | 0 | .1 |
当设定阈值为 0.9 时,只有第一个点预测为 1,其余都为 0,故 、
,计算出
,
,画出点 (0,0.1)
当设定阈值为 0.8 时,只有前两个点预测为 1,其余都为 0,故 $\#FP=0、\#TP=2$,计算出 、
,画出点 (0,0.2)
当设定阈值为 0.7 时,只有前三个点预测为 1,其余都为 0,故 、
,计算出
、
,画出点 (0.1,0.2)。
以此类推,画出的 ROC 曲线如下:
因此,在画 ROC 曲线前,需要将预测分数从大到小排序,然后将预测分数依次设定为阈值,分别计算 和
。而对于基准线,假设随机预测为正样本的概率为
,即
由于
计算的是负样本中,预测为正样本的概率,因此 FPR=
(同理,TPR=
)。所以,基准线为从点 (0, 0) 到 (1, 1) 的斜线。
3.2 Python 代码
接下来,我们将结合代码讲解如何在 Python 中绘制 ROC 曲线。
下面的代码参考了《An Introduction to ROC Analysis》[2]中的算法 1(伪代码)。值得一提的是,知名机器学习库 scikit-learn 的 roc_curve 函数[3] 也参考了这个算法。

下面我自己实现的 roc 函数可以理解为是简化版的 roc_curve,这里的代码逻辑更加简洁易懂,算法的时间复杂度 O ( n log n ) O(n\log n) O(nlogn)。
完整的代码如下:
# import numpy as np
def roc(y_true, y_score, pos_label):"""y_true:真实标签y_score:模型预测分数pos_label:正样本标签,如“1”"""# 统计正样本和负样本的个数num_positive_examples = (y_true == pos_label).sum()num_negtive_examples = len(y_true) - num_positive_examplestp, fp = 0, 0tpr, fpr, thresholds = [], [], []score = max(y_score) + 1# 根据排序后的预测分数分别计算fpr和tprfor i in np.flip(np.argsort(y_score)):# 处理样本预测分数相同的情况if y_score[i] != score:fpr.append(fp / num_negtive_examples)tpr.append(tp / num_positive_examples)thresholds.append(score)score = y_score[i]if y_true[i] == pos_label:tp += 1else:fp += 1fpr.append(fp / num_negtive_examples)tpr.append(tp / num_positive_examples)thresholds.append(score)return fpr, tpr, thresholds导入上面 3.1 表格中的数据,通过上面实现的 roc 方法,计算 ROC 曲线的坐标值。
import numpy as npy_true = np.array([1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0]
)
y_score = np.array([.9, .8, .7, .6, .55, .54, .53, .52, .51, .505,.4, .39, .38, .37, .36, .35, .34, .33, .3, .1
])fpr, tpr, thresholds = roc(y_true, y_score, pos_label=1)最后,通过 Matplotlib 将计算出的 ROC 曲线坐标绘制成图。
import matplotlib.pyplot as pltplt.plot(fpr, tpr)
plt.axis("square")
plt.xlabel("False positive rate")
plt.ylabel("True positive rate")
plt.title("ROC curve")
plt.show()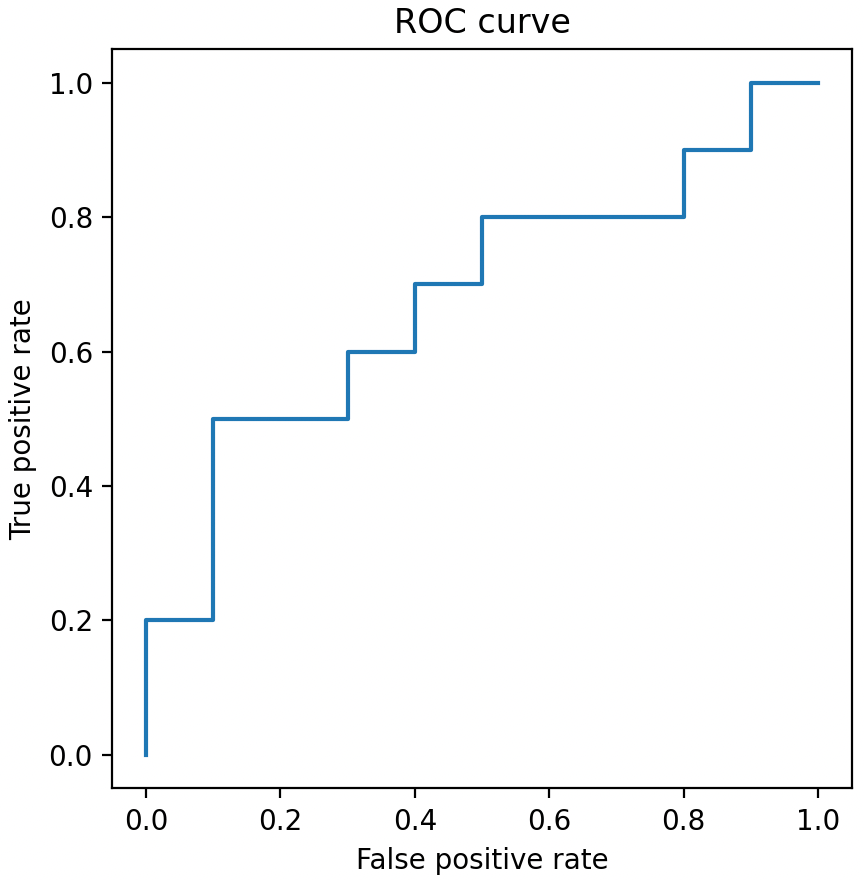
至此,ROC 的基础知识部分就全部讲完了,如果还想深入了解的同学可以继续往下看。
四、联邦学习中的 ROC 平均
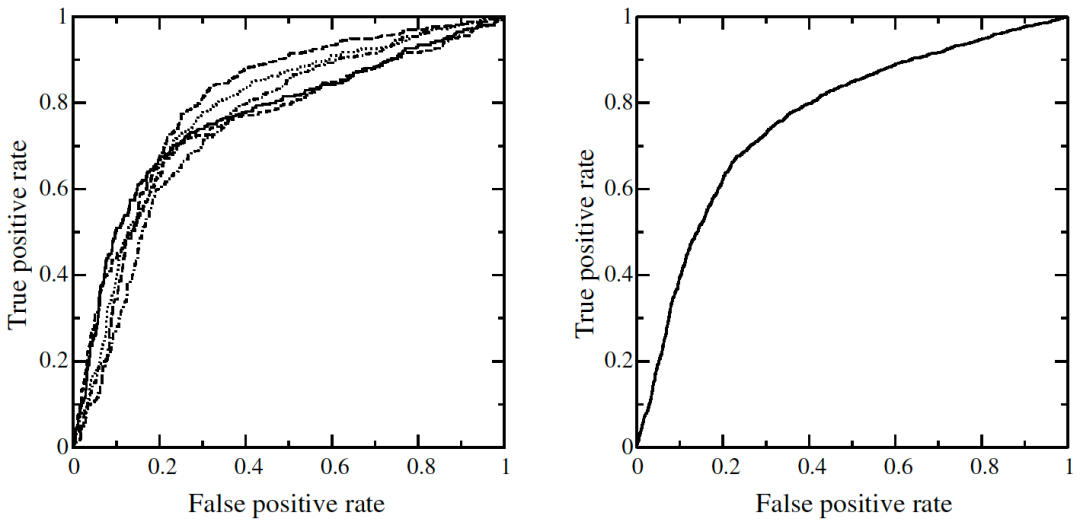
顾名思义,ROC 平均就是将多条 ROC 曲线“平均化”。那么,什么场景需要做 ROC 平均呢?例如:横向联邦学习中,由于样本都在用户本地,服务器可以采用 ROC 平均的方式,计算近似的全局 ROC 曲线。
ROC 的平均有两种方法:垂直平均、阈值平均,下面将逐一进行讲解,并给出 Python 代码实现。
4.1 垂直平均
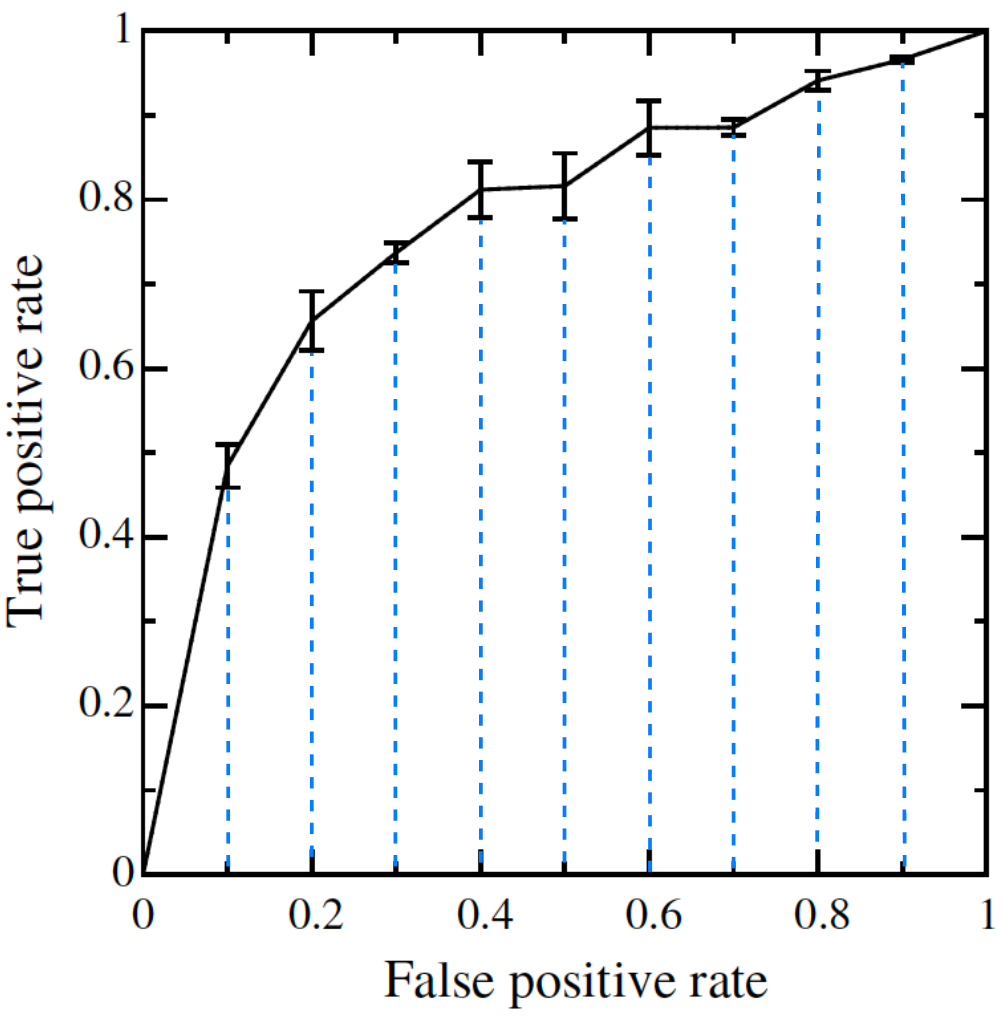
垂直平均(Vertical averaging)的思想是,选取一些 FPR 的点,计算其平均的 TPR 值。下面是论文中的算法描述的伪代码,看不懂可直接略过看 Python 代码实现部分。

下面是 Python 的代码实现:
# import numpy as np
def roc_vertical_avg(samples, FPR, TPR):"""samples:选取FPR点的个数FPR:包含所有FPR的列表TPR:包含所有TPR的列表"""nrocs = len(FPR)tpravg = []fpr = [i / samples for i in range(samples + 1)]for fpr_sample in fpr:tprsum = 0# 将所有计算的tpr累加for i in range(nrocs):tprsum += tpr_for_fpr(fpr_sample, FPR[i], TPR[i])# 计算平均的tprtpravg.append(tprsum / nrocs)return fpr, tpravg# 计算对应fpr的tpr
def tpr_for_fpr(fpr_sample, fpr, tpr):i = 0while i < len(fpr) - 1 and fpr[i + 1] <= fpr_sample:i += 1if fpr[i] == fpr_sample:return tpr[i]else:return interpolate(fpr[i], tpr[i], fpr[i + 1], tpr[i + 1], fpr_sample)# 插值
def interpolate(fprp1, tprp1, fprp2, tprp2, x):slope = (tprp2 - tprp1) / (fprp2 - fprp1)return tprp1 + slope * (x - fprp1)4.2 阈值平均
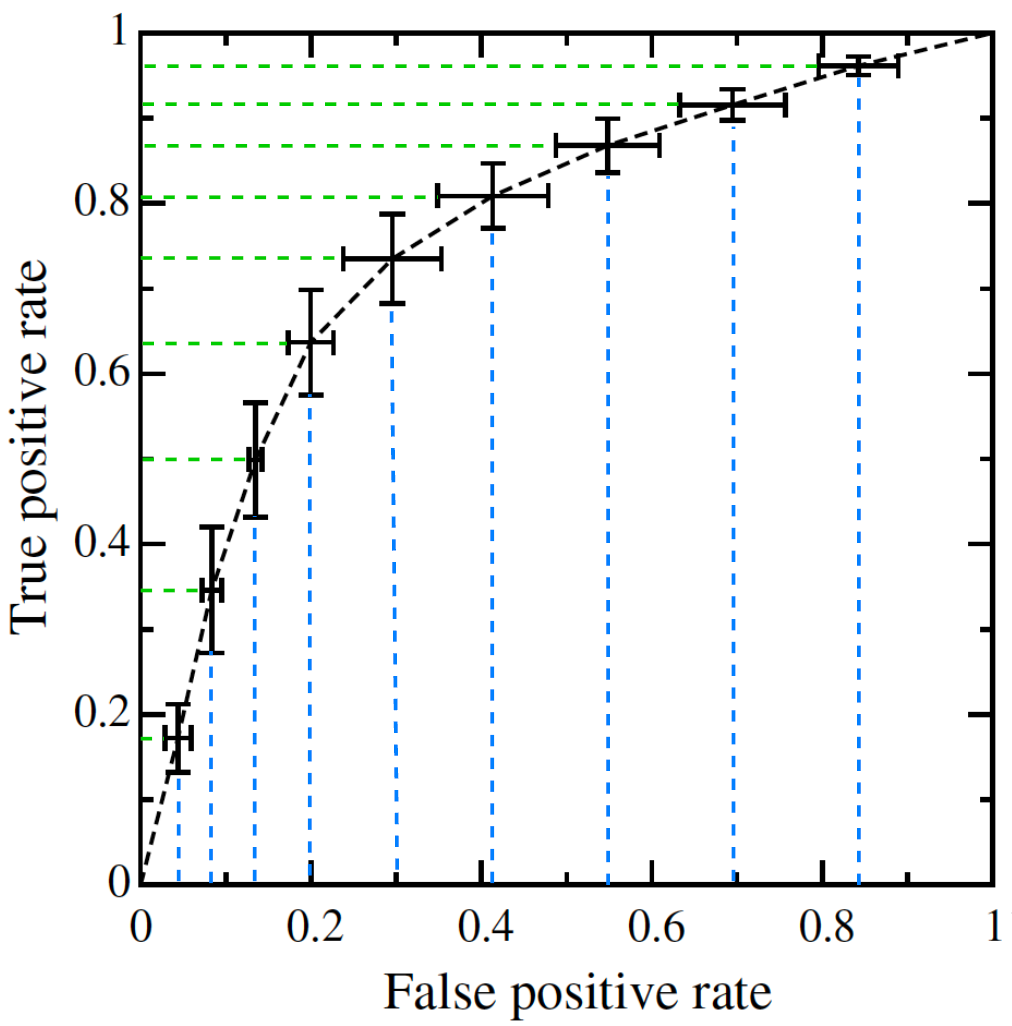
阈值平均(Threshold averaging)的思想是,选取一些阈值的点,计算其平均的 FPR 和 TPR。

下面是 Python 的代码实现:
# import numpy as np
def roc_threshold_avg(samples, FPR, TPR, THRESHOLDS):"""samples:选取FPR点的个数FPR:包含所有FPR的列表TPR:包含所有TPR的列表THRESHOLDS:包含所有THRESHOLDS的列表"""nrocs = len(FPR)T = []fpravg = []tpravg = []for thresholds in THRESHOLDS:for t in thresholds:T.append(t)T.sort(reverse=True)for tidx in range(0, len(T), int(len(T) / samples)):fprsum = 0tprsum = 0# 将所有计算的fpr和tpr累加for i in range(nrocs):fprp, tprp = roc_point_at_threshold(FPR[i], TPR[i], THRESHOLDS[i], T[tidx])fprsum += fprptprsum += tprp# 计算平均的fpr和tprfpravg.append(fprsum / nrocs)tpravg.append(tprsum / nrocs)return fpravg, tpravg# 计算对应threshold的fpr和tpr
def roc_point_at_threshold(fpr, tpr, thresholds, thresh):i = 0while i < len(fpr) - 1 and thresholds[i] > thresh:i += 1return fpr[i], tpr[i]五、最后
本文由浅入深地详细介绍了 ROC 曲线算法,包含算法原理、公式、计算、源码实现和讲解,希望能够帮助读者一口气搞懂 ROC。
虽然 ROC 是个不起眼的知识点,但能网上能彻底讲清楚 ROC 的文章并不多。所以我又花时间重温了一遍 Tom Fawcett 的经典论文《An introduction to ROC analysis》[4],并将论文的内容抽丝剥茧、配上通俗易懂的 Python 代码,最终写出了这篇文章。再次致敬🫡 Tom Fawcett,感谢他在机器学习领域的贡献!
相关文章:

ROC 曲线详解
前言 ROC 曲线是一种坐标图式的分析工具,是由二战中的电子和雷达工程师发明的,发明之初是用来侦测敌军飞机、船舰,后来被应用于医学、生物学、犯罪心理学。 如今,ROC 曲线已经被广泛应用于机器学习领域的模型评估,说…...

113.路径总和II
原题链接:113.路径总和II 需复刷 思路: 跟112.路径总和不同,该题是要你找出所有相同的路径,那么此时就要注意存储,递归和回溯了。 全代码: class Solution { public:vector<vector<int>> re…...

【Linux】WSL安装Kali及基本操作
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍WSL安装Kali及基本操作。 学其所用,用其所学。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下次更新不迷路…...
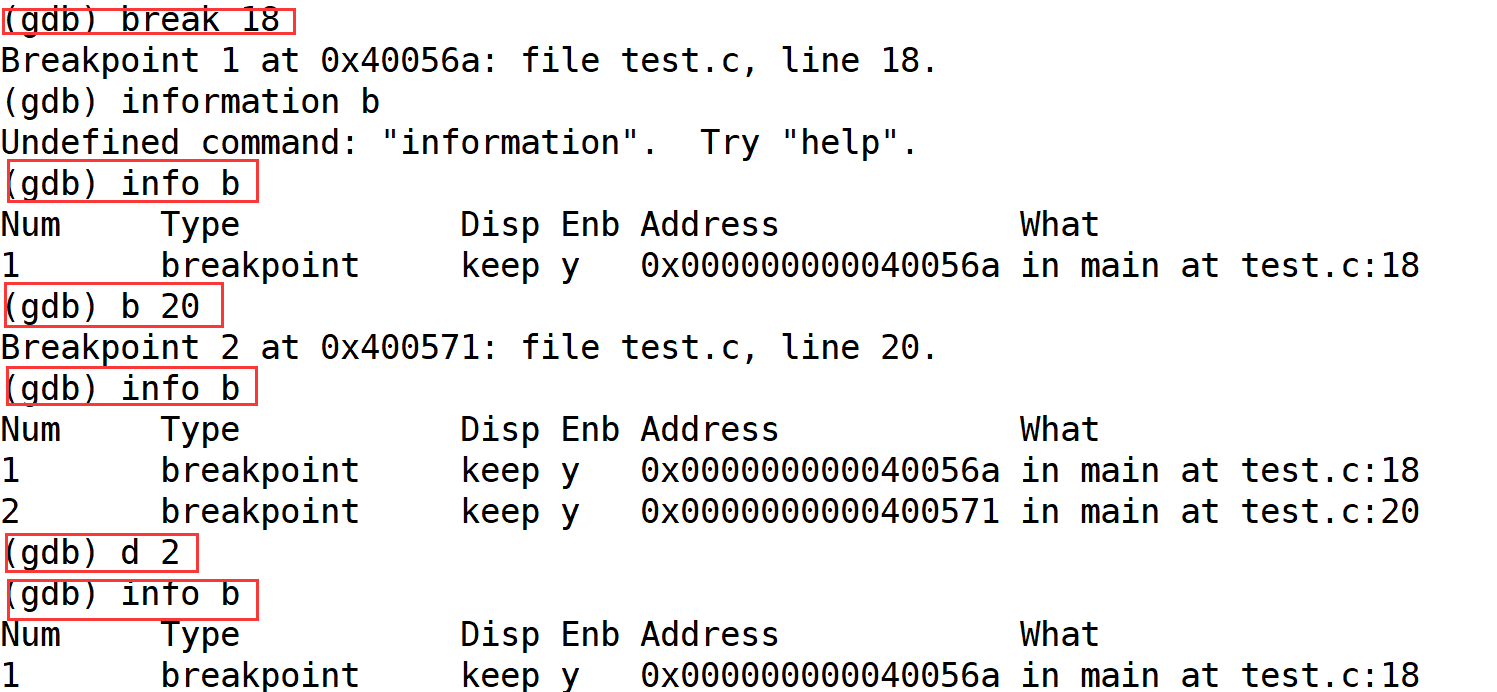
Linux基础开发工具之调试器gdb
文章目录 1.编译成的可调试的debug版本1.1gcc test.c -o testdebug -g1.2readelf -S testdebug | grep -i debug 2.调试指令2.0quit退出2.1list/l/l 数字: 显示代码2.2run/r运行2.3断点相关1. break num/b num: 设置2. info b: 查看3. d index: 删除4. n: F10逐过程5. p 变量名…...
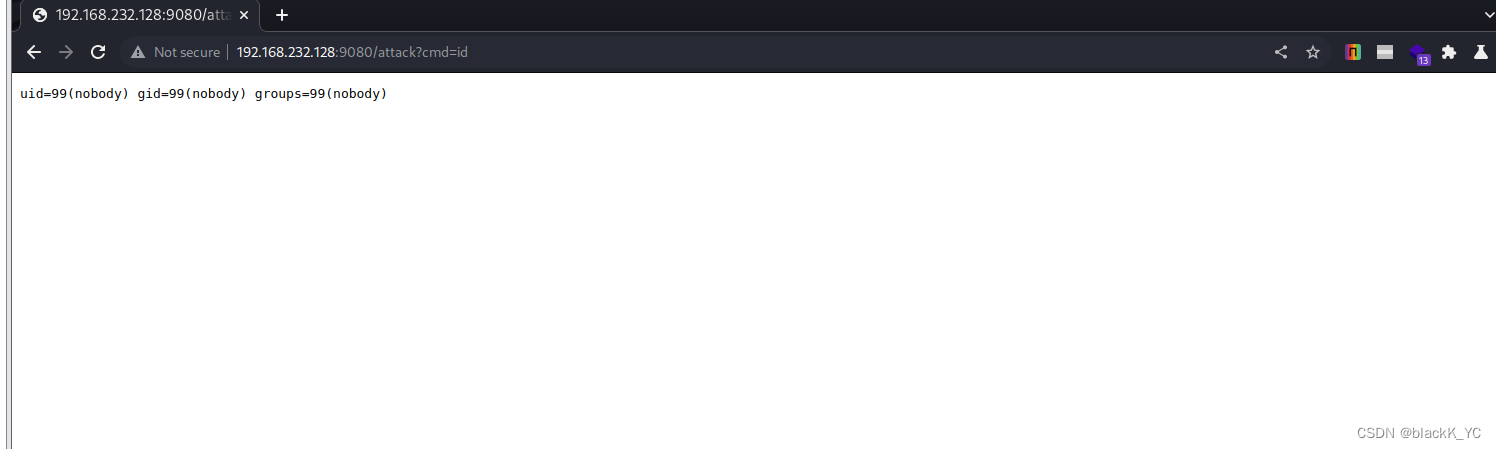
Apache APISIX 的 Admin API 默认访问令牌漏洞(CVE-2020-13945)漏洞复现
漏洞描述 Apache APISIX 是一个动态、实时、高性能的 API 网关。Apache APISIX 有一个默认的内置 API 令牌,可用于访问所有 admin API,通过 2.x 版本中添加的参数导致远程执行 LUA 代码。 漏洞环境及利用 启动docker环境 访问9080端口 通过 admin api…...
Clickhouse学习笔记(3)—— Clickhouse表引擎
前言: 有关Clickhouse的前置知识详见: 1.ClickHouse的安装启动_clickhouse后台启动_THE WHY的博客-CSDN博客 2.ClickHouse目录结构_clickhouse 目录结构-CSDN博客 Cickhouse创建表时必须指定表引擎 表引擎(即表的类型)决定了&…...

WebSocket是什么以及其与HTTP的区别
新钛云服已累计为您分享774篇技术干货 HTTP协议 HTTP是单向的,客户端发送请求,服务器发送响应。举个例子,当用户向服务器发送请求时,该请求采用HTTP或HTTPS的形式,在接收到请求后,服务器将响应发送给客户端…...

Flutter 实战:构建跨平台应用
文章目录 一、简介二、开发环境搭建三、实战案例:开发一个简单的天气应用1. 项目创建2. 界面设计3. 数据获取4. 实现数据获取和处理5. 界面展示6. 添加动态效果和交互7. 添加网络错误处理8. 添加刷新功能9. 添加定位功能10. 添加通知功能11. 添加数据持久化功能 《F…...

Python中68个内置函数的使用与归类
前言 在Python解释器中内置的、可以直接使用的函数。这些函数不需要额外的导入或安装,可以直接在Python代码中调用。Python内置函数包括了很多常用的功能,比如对数据类型的操作、数学运算、字符串处理、文件操作等。一些常见的内置函数包括print()、len…...

AGV無人搬送車控制系统Pytorn
import tkinter as tk import Main import monitoring # メインウィンドウを作成 root tk.Tk() root.title("AGV無人搬送車控制系统 ver1.0.0") # ウィンドウサイズを固定 root.geometry("501x340") root.resizable(False, False) # サイズ変更を…...
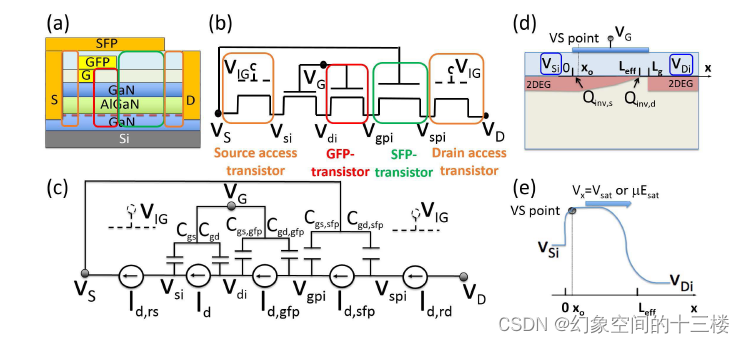
使用MVS-GaN HEMT紧凑模型促进基于GaN的射频和高电压电路设计
标题:Facilitation of GaN-Based RF- and HV-Circuit Designs Using MVS-GaN HEMT Compact Model 来源:IEEE TRANSACTIONS ON ELECTRON DEVICES(19年) 摘要—本文阐述了基于物理的紧凑器件模型在研究器件行为细微差异对电路和系统…...

Android13分享热点设置安全性为wpa3
Android13分享热点设置安全性为wpa3 文章目录 Android13分享热点设置安全性为wpa3一、前言热点WPA3加密类型是需要底层硬件支持的。Wifi WPA3 和 热点 WPA3 是不一样的分享初衷 二、代码分析1、应用代码中热点设置WPA3 加密格式报错部分日志信息: 2、系统代码分析&a…...

2023-11-12 LeetCode每日一题(Range 模块)
2023-03-29每日一题 一、题目编号 715. Range 模块二、题目链接 点击跳转到题目位置 三、题目描述 Range模块是跟踪数字范围的模块。设计一个数据结构来跟踪表示为 半开区间 的范围并查询它们。 半开区间 [left, right) 表示所有 left < x < right 的实数 x 。 实…...

【六袆 - Framework】Angular-framework;前端框架Angular发展的由来0001;
Angular发展介绍,Angular17新特性 官方文档Angular框架发展的由来何为结构化、模块化 Angular17新特性 English unit Embarking on the journey of deep technical learning requires a well-structured approach, applicable to any programming language. The key…...

JAVA集合学习
一、结构 List和Set继承了Collection接口,Collection继承了Iterable Object类是所有类的根类,包括集合类,集合类中的元素通常是对象,继承了Object类中的一些基本方法,例如toString()、equals()、hashCode()。 Collect…...
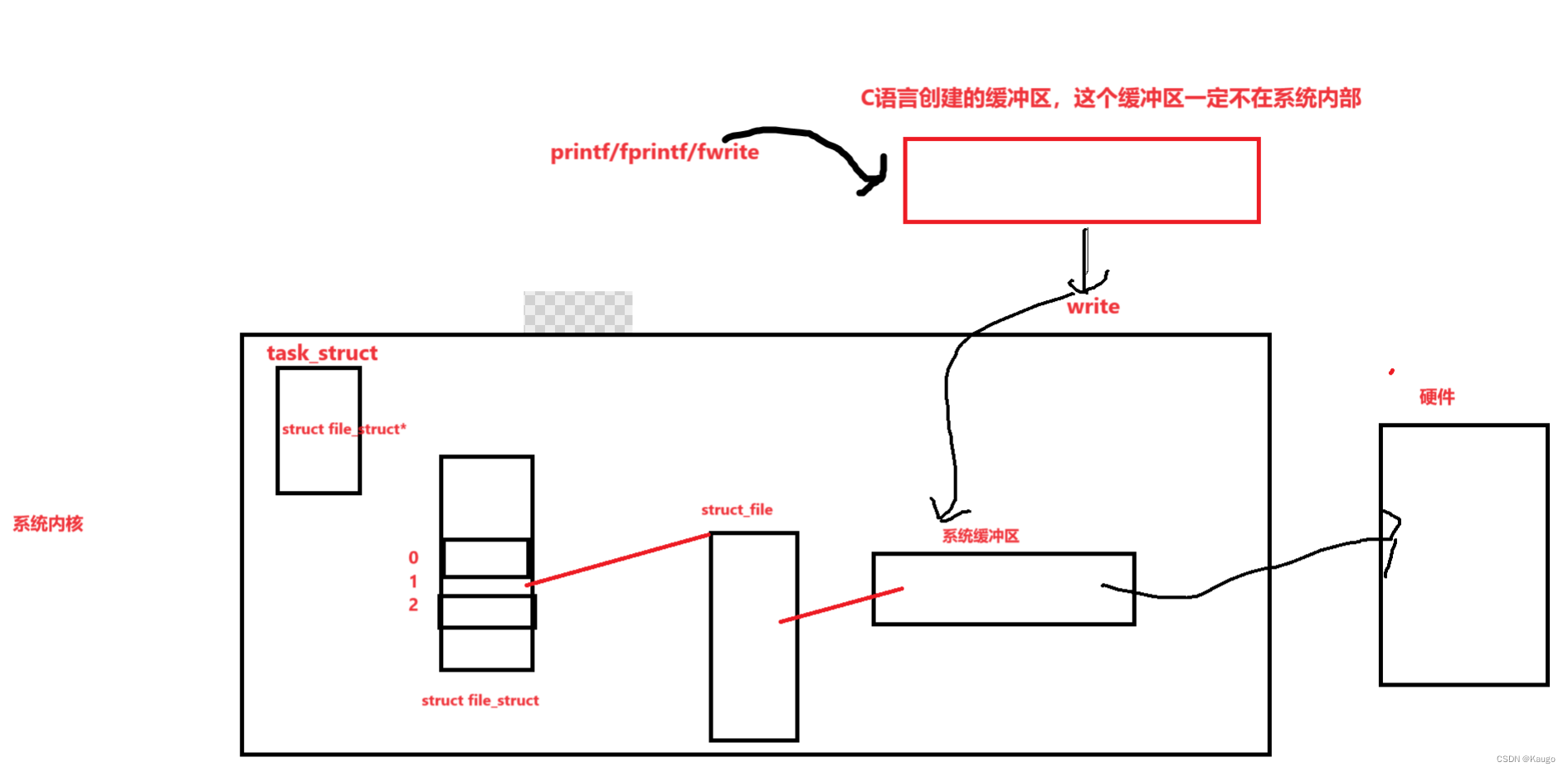
【Linux】语言层面缓冲区的刷新问题以及简易模拟实现
文章目录 前言一、缓冲区刷新方法分类a.无缓冲--直接刷新b.行缓冲--不刷新,直到碰到\n才刷新c.全缓冲--缓冲区满了才刷新 二、 缓冲区的常见刷新问题1.问题2.刷新本质 三、模拟实现1.Mystdio.h2.Mystdio.c3.main.c 前言 我们接下来要谈论的是我们语言层面的缓冲区&…...
Mac安装与配置eclipse
目录 一、安装Java:Mac环境配置(Java)----使用bash_profile进行配置(附下载地址) 二、下载和安装eclipse 1、进入eclipse的官网 (1)、点击“Download Packages ”编辑 (2)、找到macOS选择符合自己电脑的框架选项…...
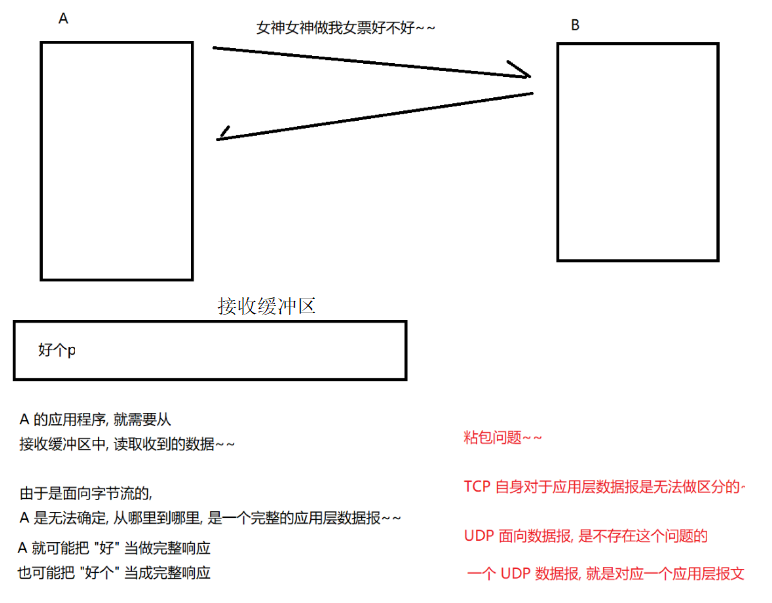
TCP协议(建议收藏)
1. TCP特点 有连接:需要双方建立连接才能通信,在socket编程中服务端new ServerSocket(port)需要绑定端口,在客服端new Socket(serverIp, serverPort)与服务端建立连接可靠传输:确认应答机制,超时重传机制面向字节流&a…...
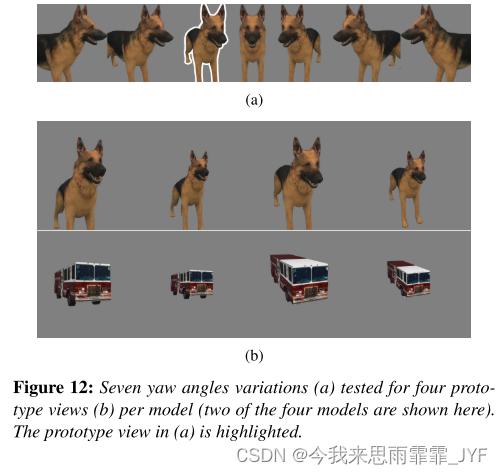
Interactive Analysis of CNN Robustness
Interactive Analysis of CNN Robustness----《CNN鲁棒性的交互分析》 摘要 虽然卷积神经网络(CNN)作为图像相关任务的最先进模型被广泛采用,但它们的预测往往对小的输入扰动高度敏感,而人类视觉对此具有鲁棒性。本文介绍了 Pert…...

Java,多线程,线程的通信机制
线程间通信的理解: 当我们需要多个线程来共同完成一件任务,并且我们希望他们有规律地执行,那么多线程之间需要一些通信机制。可以协调它们的工作,以此实现多线程共同操作一份数据。 关于线程间的通信,以下代码为例&am…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
