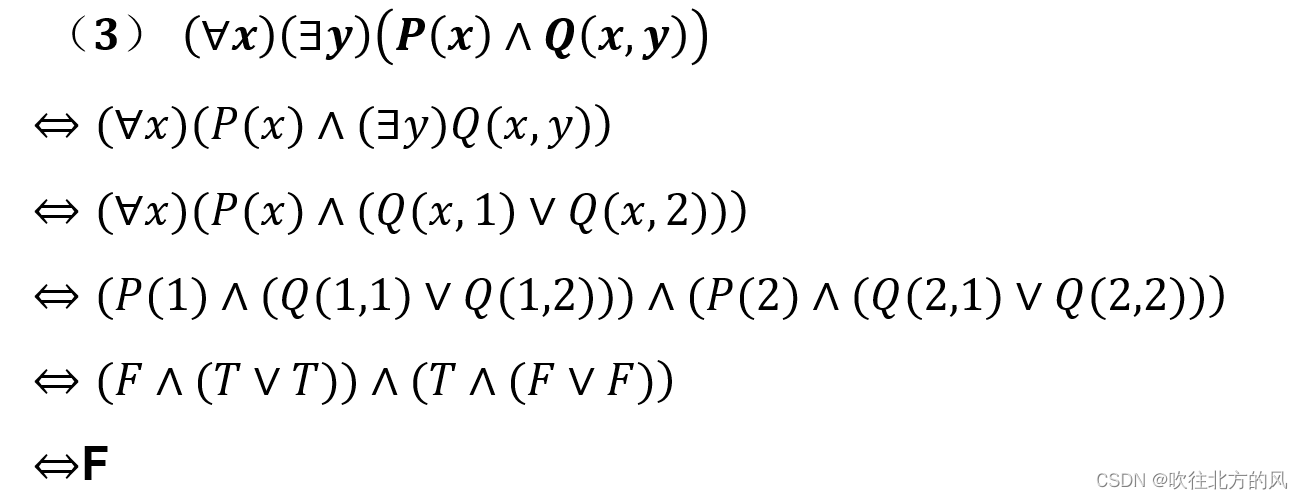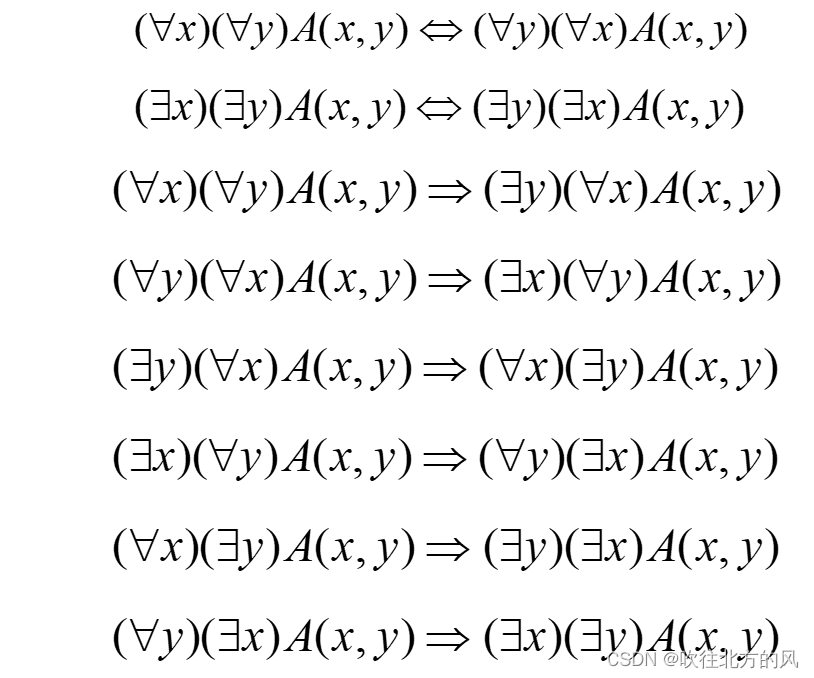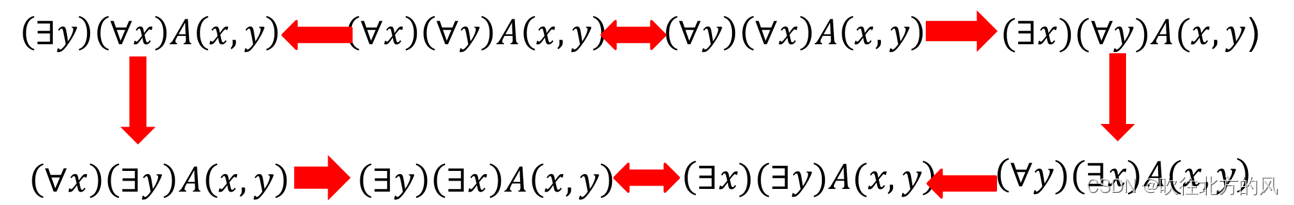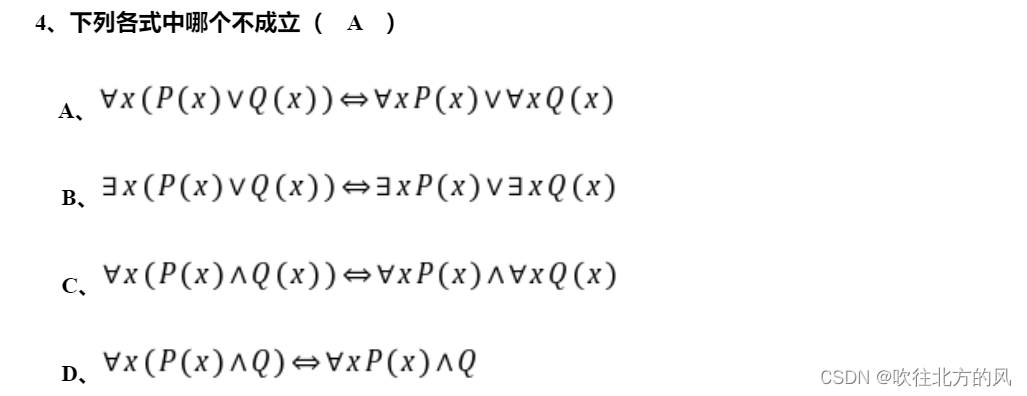【离散数学必刷题】谓词逻辑(第二章 左孝凌版)刷完包过!


专栏:离散数学必刷题
本章需要掌握的重要知识:
1.利用谓词表达式表示命题
2.变元的约束
3.谓词公式的定义、谓词公式的赋值
4.谓词公式的翻译(注意在全总个体域时使用特性谓词)
5.有限论域上量词的消去
6.谓词公式中关于量词的等价公式和蕴含式(表2-5.1)
7.前束范式 前束析取范式 前束合取范式
8.谓词推理
8种题型(速通版):
【1】用谓词表达式写出下面几个命题(都是容易写错的经典例题):
1、某些大学生运动员是国家选手。
设 S(x) : x 是大学生 。 L(x) : x 是运动员 。C(x) : x 是国家选手。
则有:
2、没有一个国家选手不是健壮的。
设 S(x) :x 是国家选手。L(x):x 是健壮的。
则有:
或者
3、所有老的国家选手都是运动员。
设 S(x) : x 是国家选手。P(x) : x 是老的 。 L(x) : x 是运动员。
则有:
4、没有一位女同志既是国家选手又是家庭妇女。
设 S(x) : x 是女同志。 P(x) : x 是国家选手 。Q(x) : x 是家庭妇女。
则有:
5、所有运动员都钦佩某些教练。
设 S(x) : x 是运动员。 P(y) : y 是教练。A(x , y) : x 钦佩 y。
则有:
6、有些大学生不钦佩运动员。
设 S(x) : x 是大学生。P(y) : y 是运动员。A(x , y) : x 钦佩 y。
则有:

【例题】
【2】利用谓词公式翻译下面几个命题:
1、如果有限个数的乘积为零,那么至少有一个因子等于零。
设 N(x) : x 是有限个数的乘积。z(y) : y 等于零 。P(x) : x 的乘积为零。F(y) : y 是乘积中的一个因子。
则有: (∀x)( N(x)∧P(x)→(∃y)( F(y)∧z(y) ) )
2、对于每个实数x,存在一个更大的实数y。
设 R(x):x 是实数。Q(x,y):y 大于 x 。
则有: (∀x)( R(x)→(∃y)( Q(x,y)∧R(y) ) )
3、存在实数x,y 和 z ,使得x 与 y之和大于 x 与 z 之积。
R(x): x 是实数 。G(x,y) : x 大于 y 。
则有:(∃x)(∃y)(∃z)( R(x) ∧ R(y) ∧ R(z) ∧ G(x+y , x⋅z) )。
【3】 对下列谓词公式中的约束变元进行换名:
1、(∀x)(∃y)(P(x,z)→Q(y))S(x,y)
则为:(∀u)(∃v)(P(u,z)→Q(v))
S(x,y)
2、((∀x)(P(x)→(R(x)∨Q(x)))∧(∃x)R(x))→(∃z)S(x,z)
则为:((∀u)(P(u)→(R(u)∨Q(u)))∧(∃v)R(v))→(∃z)S(x,z)
这里可能有些同学会疑惑了,为什么第2题的 z 变元不换名啊?
首先我们要明确进行约束变元换名的前提:
换名是为了避免出现同一个变量既是约束变元,又是自由变元的情况出现。如果不是这种情况,可以不换。
【4】对下列谓词公式中的自由变元进行代入:
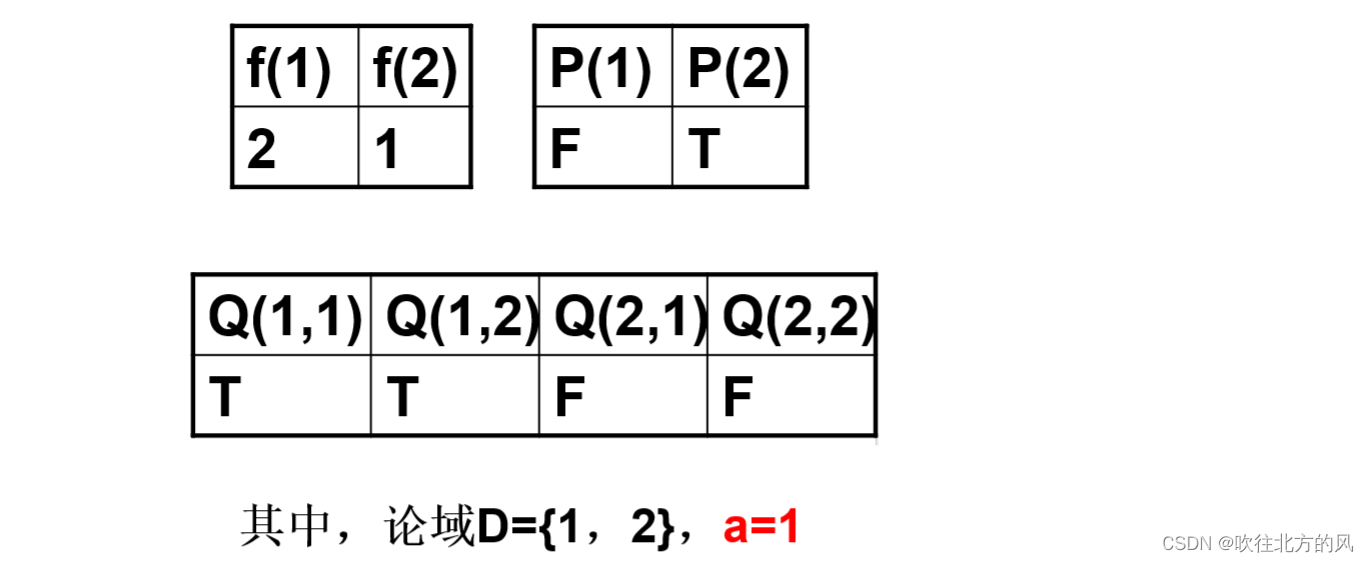
【5】 有限论域消去量词,并对以下公式赋值后求真值:
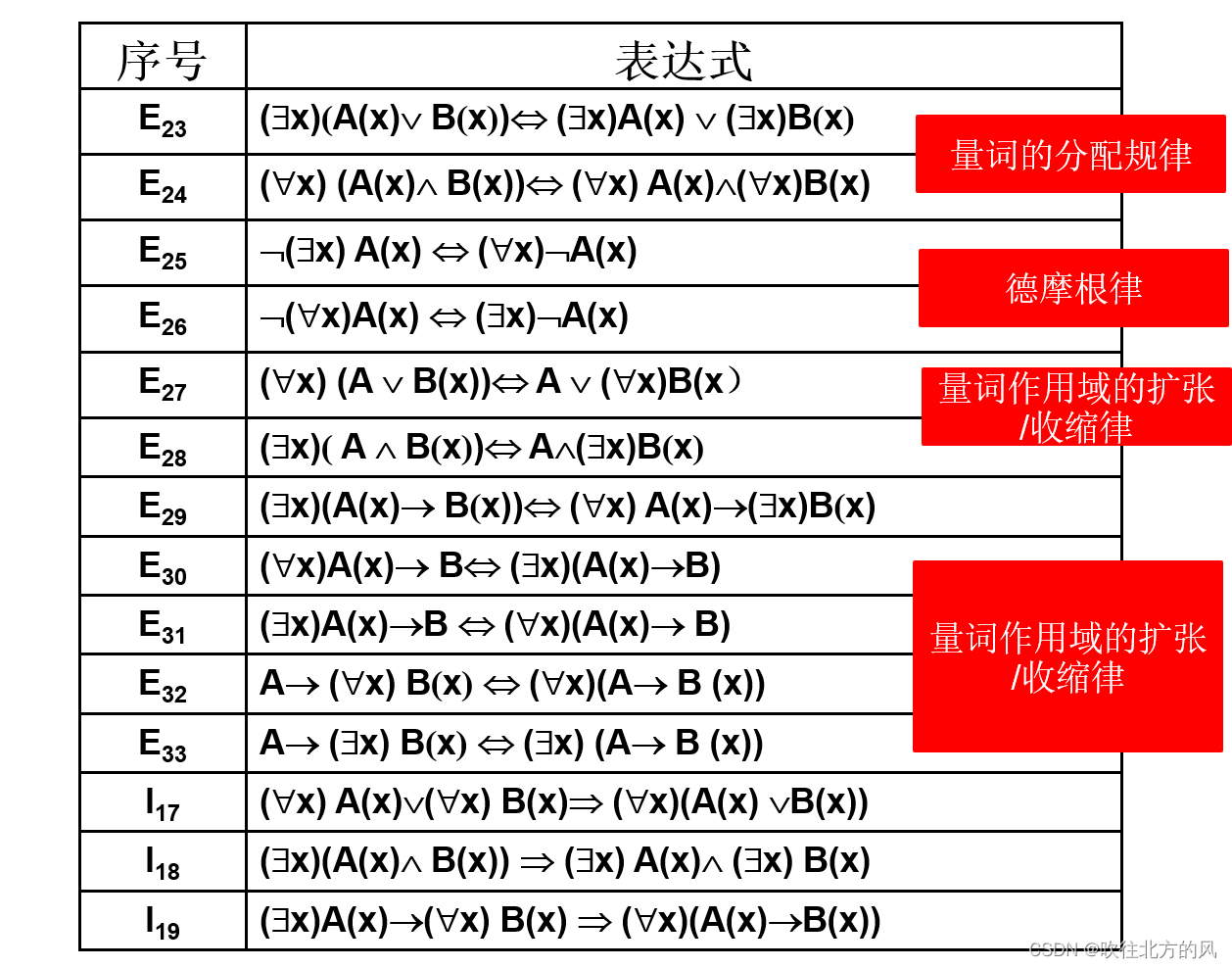
【6】 请记住以下的谓词公式的等价式和蕴含式:
⚠️注意:全称量词与存在量词在公式中出现的次序,不能随意更换。
如果你想记下这个,可以通过如下图辅助性记忆:
用双向箭头表示等价,单向箭头表示蕴含,见它们之间的关系。
【例题】
【7】 求前束合取范式:
前束合取范式的定义:(注意:可以
,也可以
,所以我们只需要简单得满足合取范式、析取范式的结构就可以了,不用满足主合取范式和主析取范式得结构哦!)
前束析取范式定义:
做题时,可能遇到的三种情况:
- 假设求出的前束合取范式,它的每一个
都唯一,那么可以采用主合取范式和主析取范式的性质:
求出前束合取范式后,根据第一章主合取范式和主析取范式的知识:
在真值表中,一个公式的真值为T的指派所对应的小项的析取,即为此公式的主析取范式。
那剩下的真值为F的指派所对应的大项的合取,即为此公式的主合取范式。
我们可以直接通过前束合取范式求出前束析取范式:
【例题】
- 假设求出的前束合取范式,存在有
不唯一,那么就硬算呗!
例如求:(∀x)(P(x)→Q(x,y))→((∃y)P(y)∧(∃z)Q(y,z)) 它的前束合取范式和前束析取范式
答:先求其前束合取范式
(∀x)(P(x)→Q(x,y))→((∃y)P(y)∧(∃z)Q(y,z))
⇔¬(∀x)(¬P(x)∨Q(x,y))∨((∃y)P(y)∧(∃z)Q(y,z))
⇔(∃x)(P(x)∧¬Q(x,y))∨((∃u)P(u)∧(∃z)Q(y,z))
⇔(∃x)(∃u)(∃z)((P(x)∧¬Q(x,y))∨(P(u)∧Q(y,z)))
我们发现P(x) 和 p(u) ,Q(x,y) 和 Q(y,z)它们的
不唯一,所以当我们再求出它得前束析取范式时,就只能将其展开,表示前束析取范式:
(∃x)(∃u)(∃z)( (P(x)∨P(u))∧(P(x)∨Q(y,z))∧(¬Q(x,y)∨P(u))∧(¬Q(x,y)∨Q(y,z)))
- ⚠️注意:
当我们求一个wff的前束合取范式或析取范式时,有些可以直接求出了它的真值(T或F),
例如求:(∃x)P(x)∨(∃x)Q(x))→(∃x)(P(x)∨Q(x))的前束合取范式和前束析取范式
则:
((∃x)P(x)∨(∃x)Q(x))→(∃x)(P(x)∨Q(x))
⇔¬((∃x)P(x)∨(∃x)Q(x))∨(∃x)(P(x)∨Q(x))
⇔¬(∃x)(P(x)∨Q(x))∨(∃x)(P(x)∨Q(x))
⇔T
那么 T 既是前束析取范式,也是前束合取范式,这就是最终结果!!!
我们知道:
单个变元既是简单合取式,又是简单析取式。把T看成简单合取式,它就构成了一个析取范式,类似的,把T 看成一个简单析取式,它就构成了一个合取范式。
因此这是一种特殊的范式。
总之,前束合取范式 <= 前束主合取范式;前束析取范式 <= 前束主析取范式,
【8】谓词演算的推理理论:
法一:直接证法
法二:间接证法
- CP规则
- 矛盾规则
结尾
这8种题型,轻轻松松拿下!!!

相关文章:

【离散数学必刷题】谓词逻辑(第二章 左孝凌版)刷完包过!
专栏:离散数学必刷题 本章需要掌握的重要知识: 1.利用谓词表达式表示命题 2.变元的约束 3.谓词公式的定义、谓词公式的赋值 4.谓词公式的翻译(注意在全总个体域时使用特性谓词) 5.有限论域上量词的消去 6.谓词公式中关于量词的等价…...

SpringBoot系列-2 自动装配
背景: Spring提供了IOC机制,基于此我们可以通过XML或者注解配置,将三方件注册到IOC中。问题是每个三方件都需要经过手动导入依赖、配置属性、注册IOC,比较繁琐。 基于"约定优于配置"原则的自动装配机制为该问题提供了一…...

vue3+ts 前端实现打印功能
1.安装插件 npm install vue3-print-nb --save 2.全局引用 import { createApp } from ‘vue’ import App from ‘./App.vue’ import print from ‘vue3-print-nb’ const app createApp(App) app.use(print) app.mount(‘#app’) 例子 <template><div><el-…...

egg.js sequelize数据库操作配置
egg.js sequelize数据库操作配置 文章目录 egg.js sequelize数据库操作配置1. 数据库配置2. 迁移配置3.数据表设计和迁移4.模型创建 1. 数据库配置 安装并配置egg-sequelize插件(它会辅助我们将定义好的 Model 对象加载到 app 和 ctx 上)和mysql2模块&a…...

vagrant安装k8s集群
目录 概述前期准备安装virtualbox安装vagrant安装gitbash 集群架构集群安装集群初始化集群测试 概述 使用vagrant、virtualbox创建。 前期准备 安装virtualbox 访问官网安装,版本7.0.10 安装vagrant 访问官网安装,版本2.3.7 安装gitbash 访问官网…...
ArcGIS进阶:水源涵养功能分级评价操作
首先抛出水源涵养重要性评价的公式:水源涵养量降雨量-蒸散发量-地表径流量,其中地表径流量降雨量*平均地表径流系数 声明:以下数据来源于来自于牛强老师书籍(城乡规划GIS技术)。 以下给出重要性评价阈值表࿱…...

数据结构与算法 | 第四章:字符串
本文参考网课为 数据结构与算法 1 第四章字符串,主讲人 张铭 、王腾蛟 、赵海燕 、宋国杰 、邹磊 、黄群。 本文使用IDE为 Clion,开发环境 C14。 更新:2023 / 11 / 12 数据结构与算法 | 第四章:字符串 字符串概念字符串字符字符…...

2023-11-rust-struct
struct 类似 schema。 ts的interface 和type struct MyStruct {width: i32,height: i32, } 创建实例 let eg1 MyStruct {width: 23,height: 22,}; struct 可以有自己的方法,并且默认第一个参数是该实例 impl MyStruct {fn can_hold(&self, instance: &…...
Docker容器编排
文章目录 基本概念Docker ComposeSwarm分布式NodeTaskservice集群搭建弹性伸缩 基本概念 针对容器生命周期的管理,对容器生命周期进行更方便更快捷的方式进行管理。 依赖管理:当一个容器必须在另一个容器运行完成后,才能运行时,…...
计算机中丢失mfc140u.dll怎么解决
mfc140u.dll是一个Microsoft Visual C库文件,主要用于MFC(Microsoft Foundation Class)应用程序的开发。它包含了MFC应用程序所需的一些常用功能,如对话框、窗口、菜单等。当mfc140u.dll丢失时,可能会导致MFC应用程序无…...
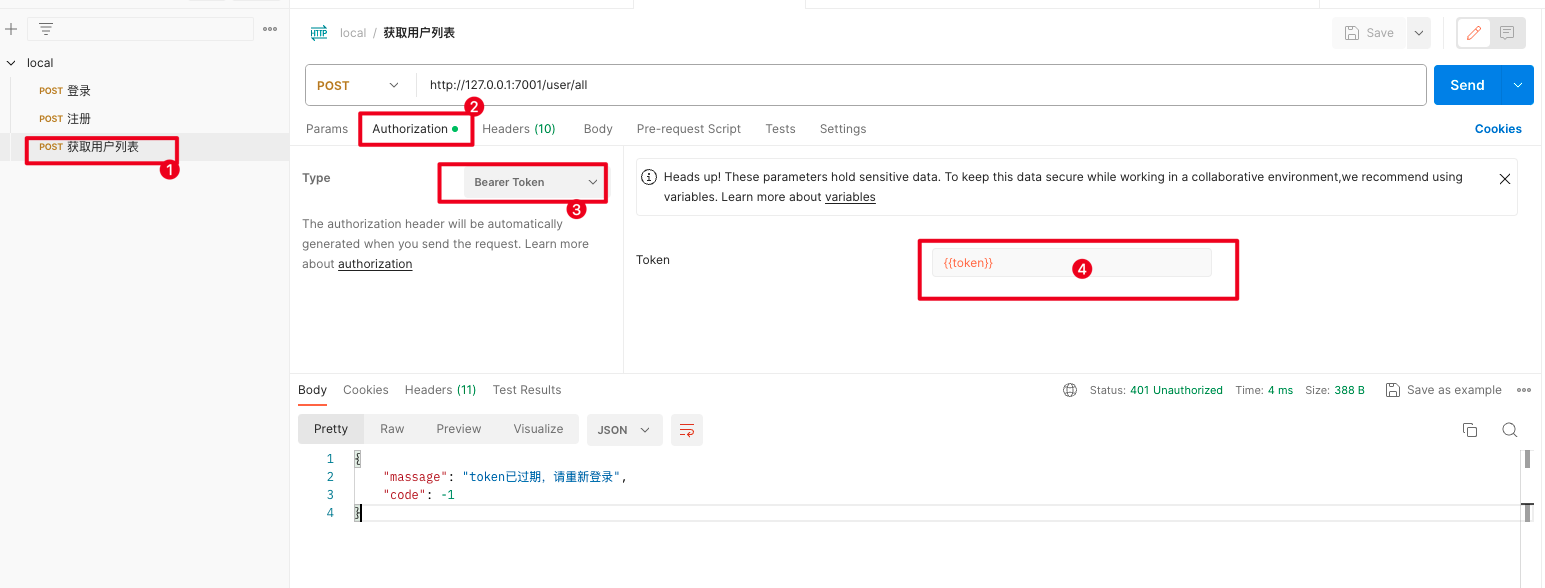
postman设置动态token, 每次登录更新token
postman设置动态token, 每次登录更新token 文章目录 postman设置动态token, 每次登录更新token问题1. 设置全局变量2. 新建登录接口3. 设置脚本4. 切换环境5. 配置动态token 问题 token过期时间一般比较短, 每次使用postman调用接口都token非常麻烦 实现token过期后, 调用一次…...
两篇)
架构师范文(AI写作)两篇
请点击↑关注、收藏,本博客免费为你获取精彩知识分享!有惊喜哟!! 架构师范文-论区块链技术及应用 2022年3月,我参与了某集团内部一款基于区块链技术的数字资产管理平台,该平台是为了方便管理公司旗下的各种…...
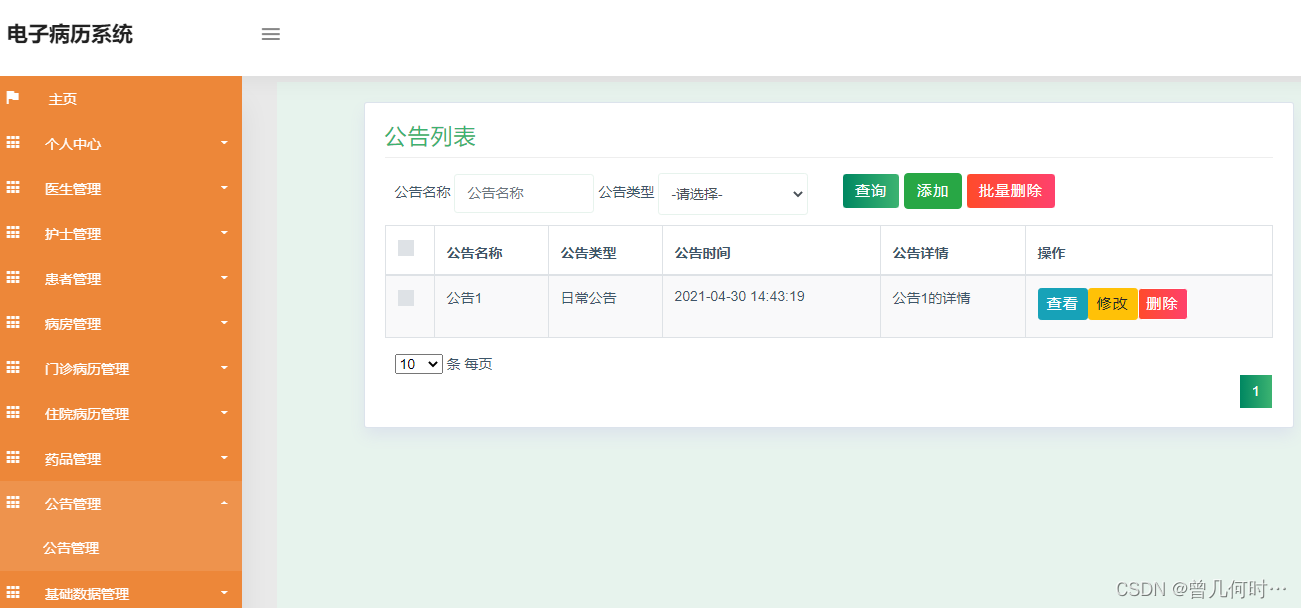
基于SSM的电子病历系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...

一次sougo workflow库的使用过程
安装就是常规的make install tutorial http_echoserver实现一下,在macos上实现 cmakelist.txt cmake_minimum_required(VERSION 3.6)set(CMAKE_BUILD_TYPE RelWithDebInfo CACHE STRING "Release")project(mainLANGUAGES C CXX )set(CMAKE_RUNTIME_OUTP…...
macOS Big Sur(macos11版本)
macOS Big Sur是苹果推出的最新操作系统,具有以下特点: 全新的设计风格:Big Sur采用了全新的设计语言,包括更加圆润的窗口和控件、更加鲜明的色彩和更加简洁的界面。这种设计风格使得操作系统更加美观和易用。强大的性能表现&…...
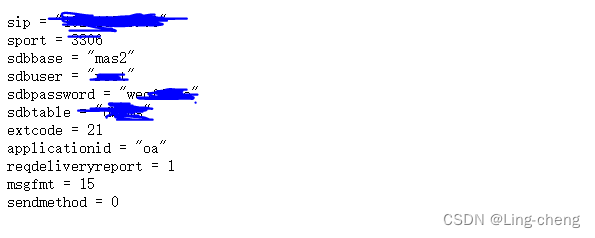
泛微E-Office信息泄露漏洞复现
简介 Weaver E-Office是中国泛微科技(Weaver)公司的一个协同办公系统。 Weaver E-Office 9.5版本存在安全漏洞。攻击者利用该漏洞可以访问文件或目录。 漏洞编号:CVE-2023-2766 漏洞复现 FOFA语法: app"泛微-EOffice&qu…...

-bash: sudo: command not found的解决方法
在 Linux 系统中,使用 sudo 命令时提示 “command not found”,首先执行以下命令看一下 /etc/sudoers.d 文件是否存在: find /etc/sudoers.d1)如果返回 No such file or directory,就说明系统没有安装sudo,…...

CMOS介绍
1 二极管 2 CMOS 2.1 栅极、源极、漏极 2.2 内部结构 2.2 导电原理 - 原理:1.通过门级和衬底加一个垂直电场Ev,从而在两口井之间形成反形层2.如果加的电场足够强,反形层就可以把source(源极)和drain(漏极…...
《软件工程与计算》期末考试真题范例及答案
今天分享一套针对《软件工程与计算》这本书的真题案例,有关《软件工程与计算》23章内容的重点知识整理,已经总结在了博客专栏中,有需要的自行阅读: 《软件工程与计算》啃书总结https://blog.csdn.net/jsl123x/category_12468792.…...
springboot高校全流程考勤系统-计算机毕设 附源码 27637
Springboot高校全流程考勤系统 摘 要 本文针对高校考勤等问题,对其进行研究分析,然后开发设计出高校全流程考勤系统以解决问题。高校全流程考勤系统系统主要功能模块包括:考勤签到、课程信息、考勤情况、申请记录列表等,系统功能设…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...