网格算法和穷举法
介绍
网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具
当需要在多个离散的点(比如网格点)中寻找最优解时,网格算法和穷举法都是常用的方法。
网格算法,也称为坐标遍历法,是一种基本的离散搜索算法。其主要思想是将区域按网格划分,并在每个网格点处对函数进行计算,从而逐个比较取得最优解。网格算法总是能找到全局最优解,但是当搜索区域维度增多时,计算时间会呈指数级增长。
穷举法,也称为暴力搜索法,其思想是将所有可能的组合情况枚举出来,最终找到最优解。穷举法的优点是可以找到所有可能的解,但其缺点是当问题规模较大时,计算量非常庞大,甚至可能无法实现。
总体而言,网格算法更适合在大多数情况下使用,而穷举法则适用于少数特定情况。
举例
假设我们要在一个二维网格中找到函数 f(x,y) = x^2 + y^2 的最小值,其中 x 和 y 的取值范围是 [-5, 5]。可以使用网格算法来实现。
% 定义函数
f = @(x, y) x.^2 + y.^2;% 定义取值范围和步长
x = -5:0.1:5;
y = -5:0.1:5;% 初始化最小值和对应的坐标
min_value = inf;
min_x = 0;
min_y = 0;% 遍历每个网格点
for i = 1:length(x)for j = 1:length(y)% 计算函数值value = f(x(i), y(j));% 更新最小值和对应的坐标if value < min_valuemin_value = value;min_x = x(i);min_y = y(j);endend
end% 输出最小值和对应的坐标
fprintf('最小值为: %.2f\n', min_value);
fprintf('对应的坐标为: (%.2f, %.2f)\n', min_x, min_y);假设我们要找到一个三位整数,使其个位数字加十位数字等于百位数字。可以使用穷举法来找到满足条件的整数。
% 穷举遍历所有三位整数
for num = 100:999% 获取个位、十位和百位数字digit1 = floor(num / 100);digit2 = floor(mod(num, 100) / 10);digit3 = mod(num, 10);% 判断是否满足条件并输出结果if digit1 + digit2 == digit3fprintf('%d\n', num);end
end相关文章:

网格算法和穷举法
介绍 网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具 当需要在多个离散的点(比如网格点)…...

【AI】自回归 (AR) 模型使预测和深度学习变得简单
自回归 (AR) 模型是统计和时间序列模型,用于根据数据点的先前值进行分析和预测。这些模型广泛应用于各个领域,包括经济、金融、信号处理和自然语言处理。 自回归模型假设给定时间变量的值与其过去的值线性相关,这使得它们可用于建模和预测时…...
)
安卓常见设计模式14------单例模式(Kotlin版)
1. W1 是什么,什么是单例模式? 单例模式属于创建型模式,旨在确保一个类只有一个实例,并提供一个全局访问点来获取该实例。单例模式的核心思想是限制类的实例化,使得系统中只有一个共享的实例。 2. W2 为什么&#…...
一维卡尔曼滤波编程实践)
卡尔曼家族从零解剖-(06)一维卡尔曼滤波编程实践
讲解关于slam一系列文章汇总链接:史上最全slam从零开始,针对于本栏目讲解的 卡尔曼家族从零解剖 链接 :卡尔曼家族从零解剖-(00)目录最新无死角讲解:https://blog.csdn.net/weixin_43013761/article/details/133846882 文末正下方中心提供了本人 联系…...

macOS使用conda初体会
最近在扫盲测序的一些知识 其中需要安装一些软件进行练习,如质控的fastqc,然后需要用conda来配置环境变量和安装软件。记录一下方便后续查阅学习 1.安装miniconda 由于我的电脑之前已经安装了brew,所以我就直接用brew安装了 brew install …...

GetPrivateProfileSection使用
基本语法 GetPrivateProfileSection 是一个 Windows API 函数,用于检索指定 INI 文件中特定节的所有键值对。它可以读取INI文件中指定节所有的键值对并将结果存储在指定的缓冲区中。 以下是 GetPrivateProfileSection 函数的基本语法: DWORD GetPriva…...

Ubuntu20.04 安装 Matlab R2021a
1. 压缩包分卷解压缩 将下载下来的压缩包分卷解压缩 Ubuntu自带的archive会解压出错,不适用于分卷解压。 需要下载7zip (sudo apt-get install 走起) zip -F xxx.zip --out XXX.zip # xxx为主文件名 # XXX.zip为输出路径,上面的…...

让35岁程序员精力充沛的方法
最近重新阅读了《掌控:开启不疲惫、不焦虑的人生》这本书。这本书曾经对我减重20斤产生了巨大的影响。自然入睡、自然醒来,能够高效地工作和享受生活,这才是我们渴望的掌控感。以下是一些笔记: 少吃比多运动更有效地控制体重 每…...
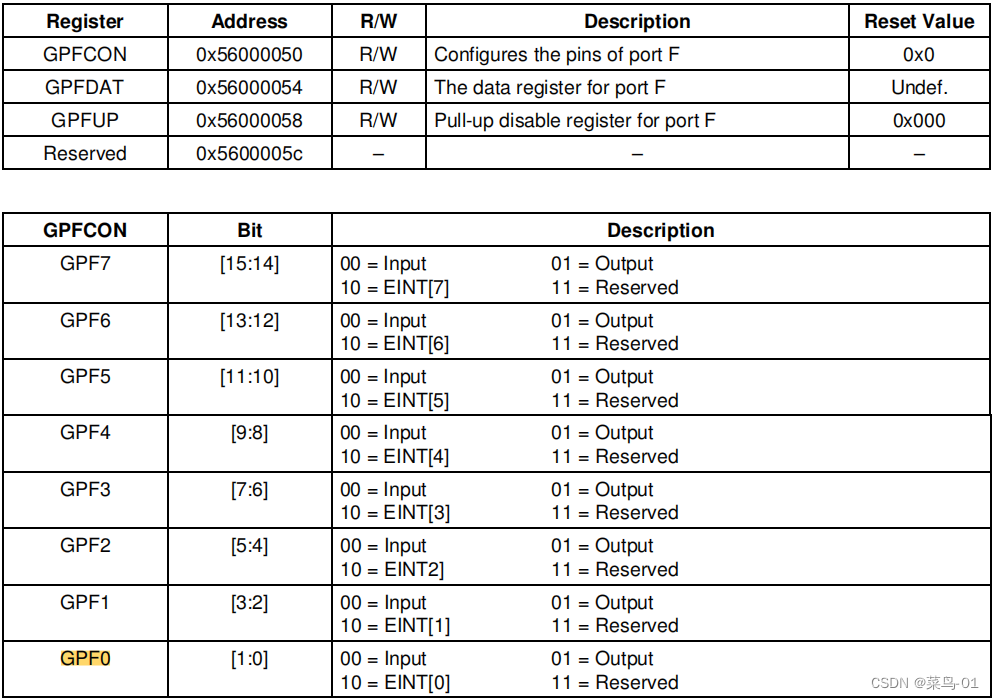
01:2440----点灯大师
目录 一:点亮一个LED 1:原理图 2:寄存器 3:2440的框架和启动过程 A:框架 B:启动过程 4:代码 5:ARM知识补充 6:c语言和汇编的应用 A:代码 B:分析汇编语言 C:内存空间 7:内部机制 二:点亮2个灯 三:流水灯 四:按键控制LED 1:原理图 2:寄存器配置 3:代码 一:点…...
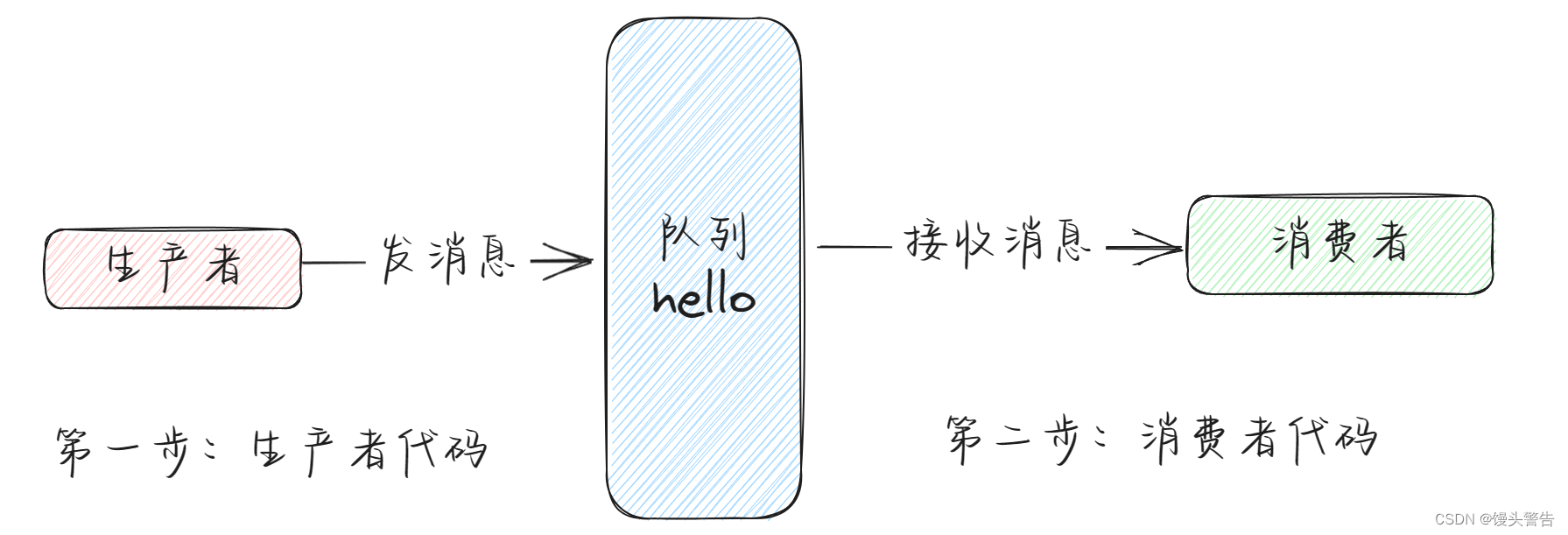
初步了解 RabbitMQ
目录 编辑一、MQ 概述 1、MQ 的简介 2、MQ 的用途 (1)限流削峰 (2)异步解耦 (3)数据收集 二、RabbitMQ 概述 1、RabbitMQ 简介 2、四大核心概念 3、RabbitMQ 的核心部分 编辑 4、名词解释: 三、Hello …...

Faster-RCNN and Mask-RCNN框架解析
由于本人记忆力实在太差,每次学完一个框架没过多久就会忘,而且码文能力不行,人又懒,所以看到了其他人写的不错的两篇框架解析的博文,先来记录一下,就当是我写的喽 Faster-rcnn详解_faster r-cnn-CSDN博客 M…...
大数据可视化数据大屏可视化模板【可视化项目案例-05】
🎉🎊🎉 你的技术旅程将在这里启航! 🚀🚀 本文选自专栏:可视化技术专栏100例 可视化技术专栏100例,包括但不限于大屏可视化、图表可视化等等。订阅专栏用户在文章底部可下载对应案例源码以供大家深入的学习研究。 🎓 每一个案例都会提供完整代码和详细的讲解,不…...

Vue Router active-class 属性
active-class 是 vue-router 模块的 router-link 组件的属性,当 router-link 标签被点击时将会应用这个样式。 单独在 router-link 标签上使用 active-class 属性 <router-link to"/about" active-class"active">about</router-link…...
Error creating bean with name ‘apiModelSpecificationReader‘ defined in URL
问题: 启动项目的时候,报错了 org.springframework.beans.factory.UnsatisfiedDependencyException: Error creating bean with name apiModelSpecificationReader defined in URL [jar:file:/D:/.gradle/caches/modules-2/files-2.1/io.springfox/sp…...

CS224W6.2——深度学习基础
在本文中,我们回顾了深度学习的概念和技术,这些概念和技术对理解图神经网络至关重要。从将机器学习表述为优化问题开始,介绍了目标函数、梯度下降、非线性和反向传播的概念。 文章目录 1. 大纲2. 优化问题2.1 举例损失函数 3. 如何优化目标函…...

Linux c/c++服务器开发实践
在Linux C开发环境中,通常有两种方式来开发多线程程序,一种是利用POSIX多线程 API函数来开发多线程程序,另外一种是利用C自带线程类来开发程序。 常见的与线程相关的基本API函数: API函数含义pthread_create创建线程pthread_exi…...

2023年11月在线IDE流行度最新排名
点击查看最新在线IDE流行度最新排名(每月更新) 2023年11月在线IDE流行度最新排名 TOP 在线IDE排名是通过分析在线ide名称在谷歌上被搜索的频率而创建的 在线IDE被搜索的次数越多,人们就会认为它越受欢迎。原始数据来自谷歌Trends 如果您相…...

视频批量剪辑:视频嵌套合并实战指南,剪辑高手速成秘籍
随着社交媒体的兴起,视频制作的需求越来越广泛。无论是个人用户还是专业团队,都需要对视频进行剪辑以符合其需求。而在这个过程中,批量剪辑视频的能力就变得至关重要。视频批量剪辑是指在一次操作中处理多个视频文件的剪辑。通过使用专业的视…...

每天一点python——day66
#每天一点Python——66 #字符串的分隔 #如图: #方法①split()从左开始分隔,默认空格为分割字符,返回值是一个列表 shello world jisuanji#首先创建一个字符串 list1s.split() print(list1)#输出结果是:[hello, world, jisuanji]注…...

搭建产品帮助中心其实很简单,方法都在这了!
网站帮助中心是一个为用户提供支持和解答问题的重要资源。它不仅可以提高用户体验,还能减少用户问题反馈的数量。通过提供清晰、易于理解的文档和指南,帮助中心可以帮助用户更好地了解产品或服务,并解决他们在使用过程中遇到的问题。接下来我…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...
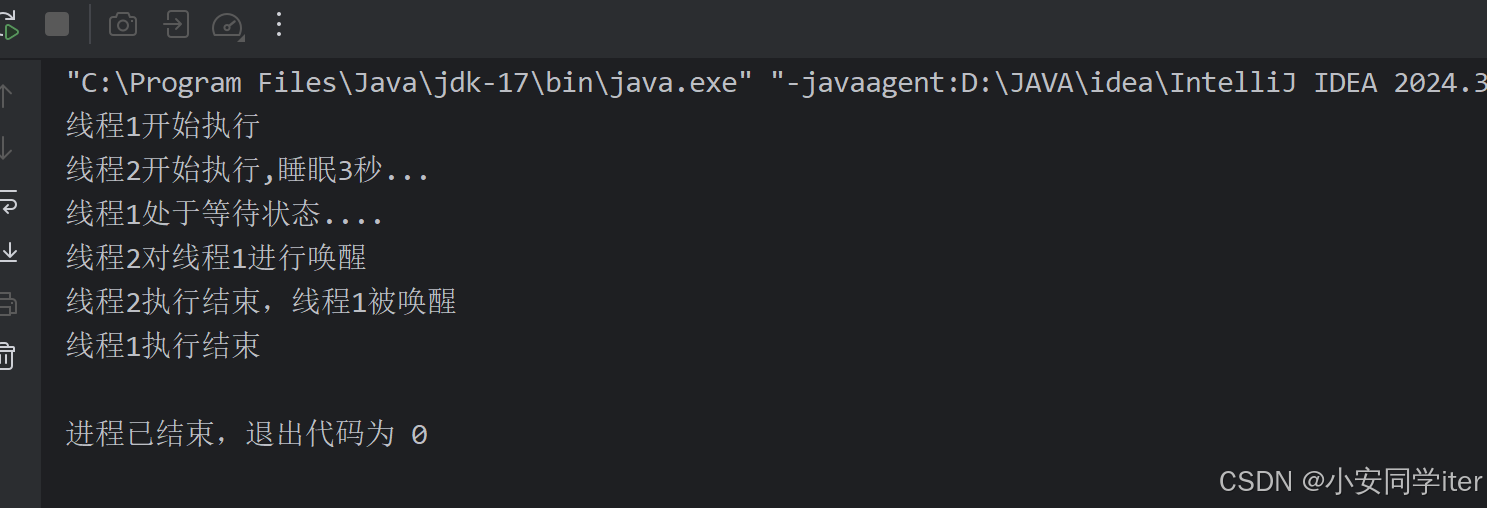
JUC并发编程(二)Monitor/自旋/轻量级/锁膨胀/wait/notify/锁消除
目录 一 基础 1 概念 2 卖票问题 3 转账问题 二 锁机制与优化策略 0 Monitor 1 轻量级锁 2 锁膨胀 3 自旋 4 偏向锁 5 锁消除 6 wait /notify 7 sleep与wait的对比 8 join原理 一 基础 1 概念 临界区 一段代码块内如果存在对共享资源的多线程读写操作…...
