[C国演义] 第十八章
第十八章
- 最长斐波那契子序列的长度
- 最长等差数列
- 等差序列划分II - 子序列
最长斐波那契子序列的长度
力扣链接

- 子序列 ⇒ dp[i] — —
以 arr[i] 结尾的所有子序列中, 斐波那契子序列的最长长度 - 子序列 ⇒ 状态转移方程 — —
根据最后一个位置的组成来划分


- 初始化 — — 根据状态转移方程, 全都初始化为
2 - 遍历顺序 — — 根据状态转移方程,
从前往后 - 返回结果 — — 返回dp表中的最大值, 记作res; 如果res < 3, 那就返回0, 如果res > 3, 那就返回res
class Solution {
public:int lenLongestFibSubseq(vector<int>& arr) {int n = arr.size();// 建表 + 初始化vector<vector<int>> dp(n, vector<int>(n, 2));// 记录返回结果int res = 2;// 优化unordered_map<int, int> hash; // <数组元素, 下标>for(int i = 0; i < n; i++){hash[arr[i]] = i;}// 填表for(int j = 2; j < n; j++) // 最后一个元素{for(int i = 1; i < j; i++) // 倒数第二个元素{int target = arr[j] - arr[i]; // 第一个元素// 斐波那契数列 -- 递增的if(target < arr[i] && hash.count(target)){dp[i][j] = dp[hash[target]][i] + 1;}res = max(res, dp[i][j]);}}// 返回结果return res < 3 ? 0 : res;}
};
最长等差数列
力扣链接

-
子序列 ⇒ dp[i]的含义:
dp[i]的含义: 以nums[i] 为结尾的所有子序列中, 等差子序列的最长长度 -
子序列 ⇒ 状态转移方程 :


-
初识化 :
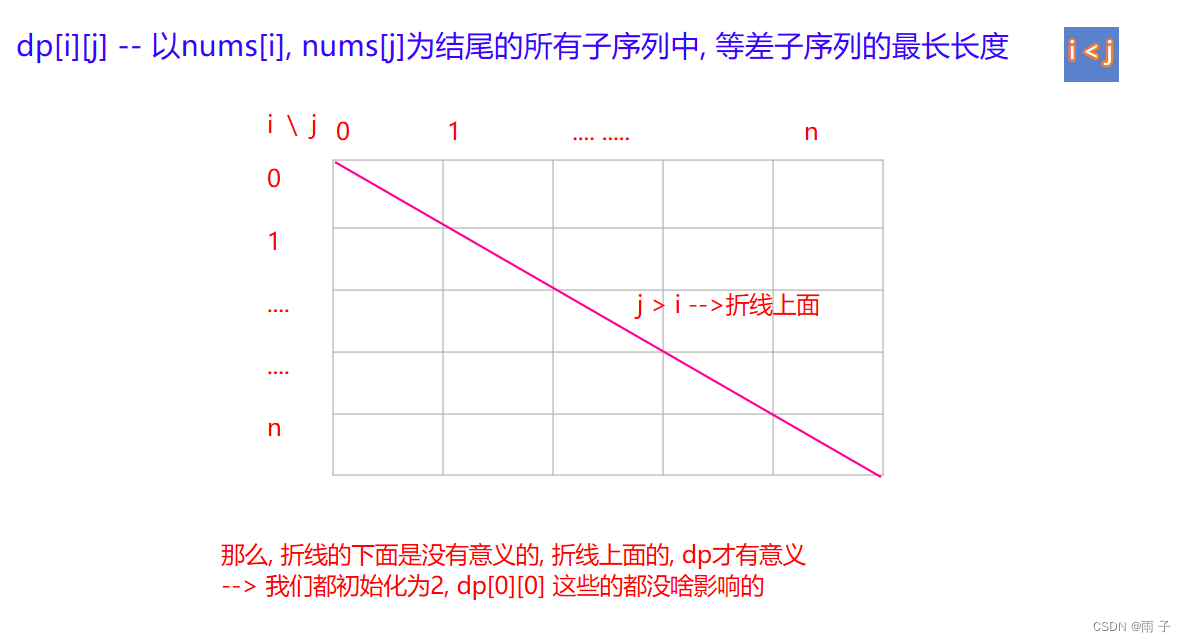
都初始化为 2
🗨️dp[0][0] 也 初始化为 2? -
-
遍历顺序 : 根据
优化, 我们采取固定第二个元素, 再枚举最后一个元素的遍历顺序 -
返回结果 :
返回dp表中的最大值
class Solution {
public:int longestArithSeqLength(vector<int>& nums) {int n = nums.size();// 建表 + 初始化vector<vector<int>> dp(n, vector<int>(n, 2));// 优化unordered_map<int, int> hash; // <数组元素, 下标>hash[nums[0]] = 0;int res = 2;// 先固定倒数第二个元素,在枚举最后一个元素 && 边dp边插入hash// -- 有利于找到离i最近的一个targetfor(int i = 1; i < n; i++) // 先固定倒数第二个元素{for(int j = i + 1; j < n; j++) // 枚举最后一个元素{int target = 2 * nums[i] - nums[j]; // 目标的第一个元素if(hash.count(target)) // 如果存在, 更新dp[i][j]{dp[i][j] = dp[hash[target]][i] + 1;}res = max(res, dp[i][j]);}// 依次插入hash表中hash[nums[i]] = i;}return res;}
};
等差序列划分II - 子序列
力扣链接

- 子序列 ⇒ dp[i] :
以nums[i] 为结尾的所有子序列中, 等差子序列的最大数目 - 子序列 ⇒ 状态转移方程 :
根据最后一个位置划分



- 初始化 :
全都初始化为 0 - 遍历顺序 :
根据优化 ⇒ 先固定倒数第二个元素, 再枚举最后一个元素 - 返回结果 :
累加dp表
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();// 建表 + 初始化vector<vector<int>> dp(n, vector<int>(n, 0));// 优化// 由于前面存在多个target && 我们要全部累加起来// --> 所以, 用一个vector来接收一下下标unordered_map<long long int, vector<int>> hash; // <数组元素, 下标>hash[nums[0]].push_back(0);int res = 0;// 先固定倒数第二个元素,在枚举最后一个元素 && 边dp边插入hashfor(int i = 1; i < n; i++) // 先固定倒数第二个元素{for(int j = i + 1; j < n; j++) // 枚举最后一个元素{long long int target = (long long int ) 2 * nums[i] - nums[j]; // 目标的第一个元素if(hash.count(target)) // 如果存在, 更新dp[i][j]{// 这里的 k 都是在合理区间内的, 全部累加for(auto k : hash[target]){// 全部都累加起来dp[i][j] += dp[k][i] + 1;}}res += dp[i][j];}// 依次插入hash表中hash[nums[i]].push_back(i);}return res;}
};
宣室求贤访逐臣,贾生才调更无伦。
可怜夜半虚前席,不问苍生问鬼神。
— — 李商隐《贾谊》
相关文章:

[C国演义] 第十八章
第十八章 最长斐波那契子序列的长度最长等差数列等差序列划分II - 子序列 最长斐波那契子序列的长度 力扣链接 子序列 ⇒ dp[i] — — 以 arr[i] 结尾的所有子序列中, 斐波那契子序列的最长长度子序列 ⇒ 状态转移方程 — — 根据最后一个位置的组成来划分 初始化 — — 根…...

发送失败的RocktMQ消息,你遇到过吗?
背景 需要通过flink同时向测试和线上的RocketMQ中写入数据 现象 在程序中分别创建了两个MqProducer,设置了不同的nameServerAddr,分别调用不同的producer向不同环境发消息,返回发送成功,但是在线上MQ中却查不到数据࿰…...

Unity中全局光照GI的总结
文章目录 前言一、在编写Shader时,有一些隐蔽的Bug不会直接报错,我们需要编译一下让它显示出来,方便修改我们选择我们的Shader,点击编译并且展示编译后的Shader后的内容,隐蔽的Bug就会暴露出来了。 二、我们大概回顾一…...

毫米波雷达技术在自动驾驶中的关键作用:安全、精准、无可替代
自动驾驶技术正以前所未有的速度不断演进,而其中的关键之一就是毫米波雷达技术。作为自动驾驶系统中的核心感知器件之一,毫米波雷达在保障车辆安全、实现精准定位和应对复杂环境中发挥着不可替代的作用。本文将深入探讨毫米波雷达技术在自动驾驶中的关键…...

Jetson平台180度鱼眼相机畸变校正调试记录
1.需求说明 由于使用180度GMSL鱼眼相机,畸变很大; 如需算法使用,必须进行畸变校正 2. 硬件说明 相机: 森云 SG2-AR0233-5300-GMSL2-190H 主板: Jetson NX 3. opencv畸变矫正处理 3.1 获取内参系数 现在森云相机可以直接读取内部flash获取内参系数 3.2 畸变处理 …...
axios请求的问题
本来不想记录,但是实在没有办法,因为总是会出现post请求,后台接收不到数据的情况,还是记录一下如何的解决的比较好。 但是我使用export const addPsiPurOrder data > request.post(/psi/psiPurOrder/add, data); 下面是封装的代码。后台接…...

【pandas刷题系列】Leetcode Problem: [595. 大的国家]
Problem: 595. 大的国家 文章目录 思路解题方法复杂度Code 思路 筛选出对应的数据,然后将不需要的列去除 解题方法 筛选出对应的数据,然后将不需要的列去除 复杂度 时间复杂度: O ( n ) O(n) O(n) 空间复杂度: O ( n ) O(n) O(n) Code import pandas a…...

【打卡】牛客网:BM46 最小的K个数
资料: 1. 排序 sort(name.begin(),name.end()); //升序 sort(name.rbegin(),name.rend()); //降序 【C】vector数组排序_vector排序_比奇堡咻飞兜的博客-CSDN博客 2. 把v2的部分值赋给v1 v1.assign(v2.begin(), v2.end()); // 用新元素替换vector 中的元素。…...

Android各类View触摸监听器失效
在XML布局中出现重叠的View,位置靠后定义的View会覆盖住位置靠前的View;即靠后的View会拦截触碰事件导致靠前的View无法收到触碰事件,无法触发监听器。 //例.<?xml version"1.0" encoding"utf-8"?> <android…...

未整理的知识链接
【scala】下划线用法总结 【scala】下划线用法总结_scala 下划线-CSDN博客 Spark Sql Row 的解析 Spark Sql Row 的解析 - 简书 spark dataframe foreach spark dataframe foreach_mob64ca12f0cf8f的技术博客_51CTO博客 spark- Dataframe基本操作-查询 https://blog.csdn.n…...
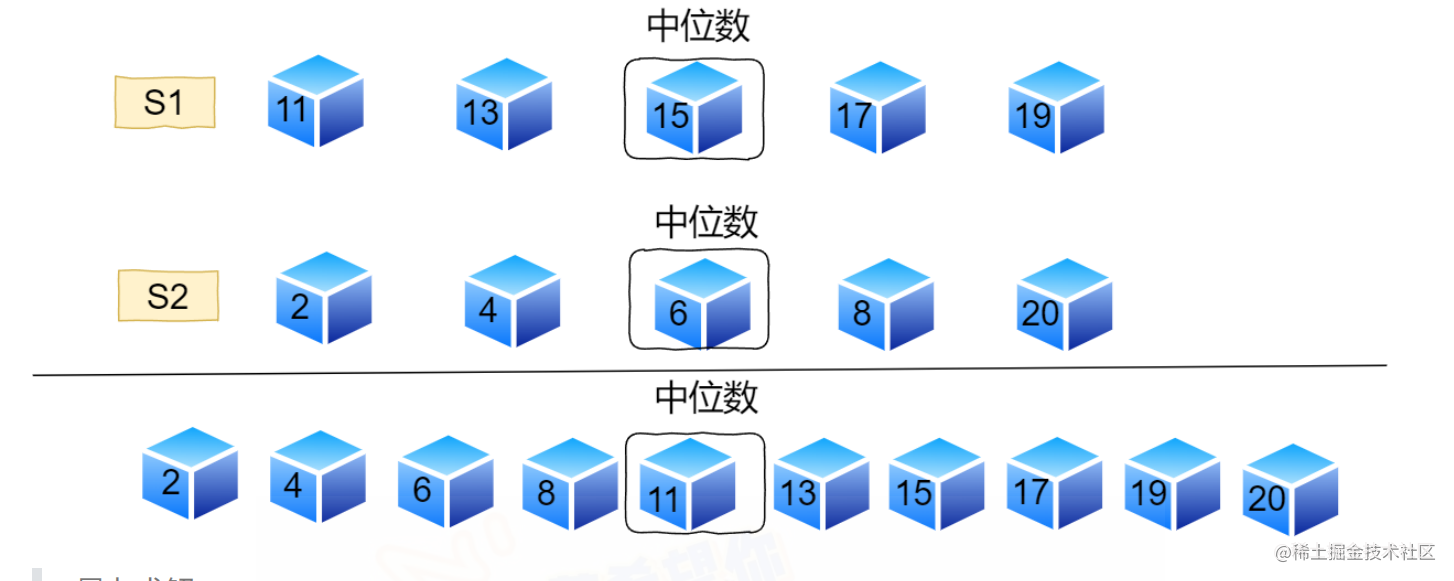
【2011年数据结构真题】
41题 41题解答: (1)图 G 的邻接矩阵 A 如下所示: 由题意得,A为上三角矩阵,在上三角矩阵A[6][6]中,第1行至第5行主对角线上方的元素个数分别为5, 4, 3, 2, 1 用 “ 平移” 的思想,…...
【科研绘图】MacOS上的LaTeX公式插入工具——LaTeXiT
在Mac上经常用OmniGraffle绘图,但是有个致命缺点是没办法插入LaTeX公式,很头疼。之前有尝试用Pages文稿插入公式,但是调字体和颜色很麻烦。并且,PPT中的公式插入感觉也不太好看。 偶然机会了解到了LaTeXiT这个工具,可…...

仓库自动化中的RFID技术的应用浅谈
仓库自动化与RFID技术的结合代表着现代供应链管理的一个重要革新。这两者的协同作用能够显著提升仓储效率、降低成本、增强库存管理、提高货物跟踪的准确性,并且使仓库操作更加智能化。 仓库自动化是一种通过应用自动化技术和系统来管理和优化仓库操作的方法。这种…...
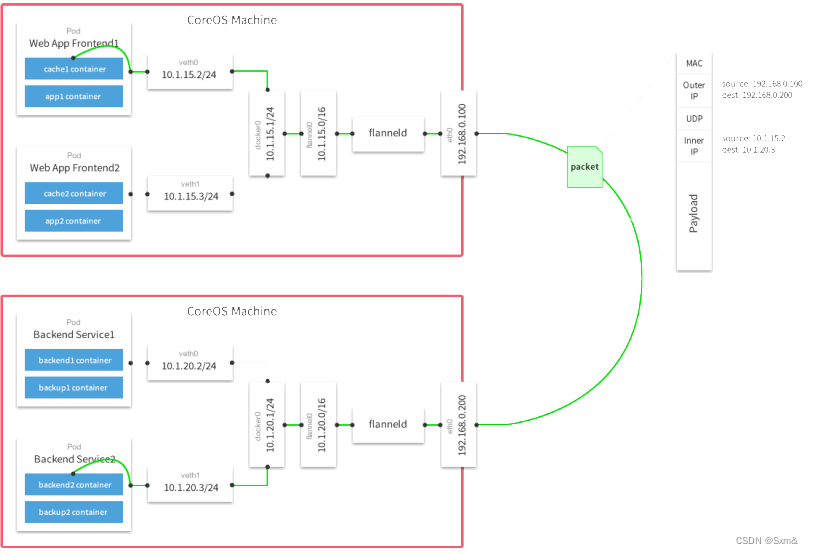
容器网络-Underlay和Overlay
一、主机网络 前面讲了容器内部网络,但是容器最终是要部署在主机上,跨主机间的网络访问又是怎么样的,跨主机网络主要有两种方案。 二、 Underlay 使用现有底层网络,为每一个容器配置可路由的网络IP。也就是说容器网络和主机网络…...
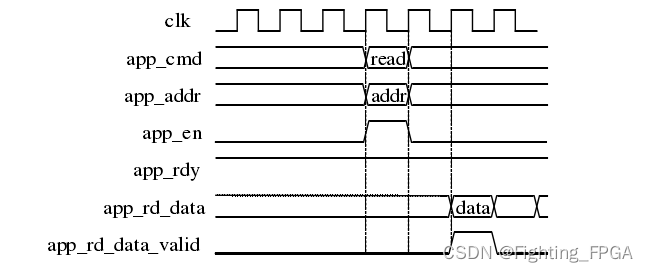
基于FPGA的PCIe-Aurora 8/10音频数据协议转换系统设计阅读笔记
文章可知网下载阅读,该论文设计了一种 PC 到光纤模块(基于Aurora的光纤传输)的数据通路,成功完成了Aurora 以及 DDR 等模块的功能验证。 学习内容: 本次主要学习了Pcie高速串行总线协议、Aurora高速串行总线协议、DDR相…...

stm32控制舵机sg90
一、sg90简介 首先介绍说一下什么是舵机。舵机是一种位置(角度)伺服的驱动器。适用于一些需要角度不断变化的,可以保持的控制系统。sg90就是舵机的一种。 舵机的工作原理比较简单。舵机内部有一个基准电压,单片机产生的PWM信号通…...
state 和 props 有什么区别?
一、state 一个组件的显示形态可以由数据状态和外部参数所决定,而数据状态就是 state,一般在 constructor 中初始化 当需要修改里面的值的状态需要通过调用 setState 来改变,从而达到更新组件内部数据的作用,并且重新调用组件 r…...

Unity 获取桌面路径的方法
在Unity中,当我们碰到以下一些情况时,可能需要桌面的路径。 1、文件操作:如果我们想在游戏中保存或读取文件到桌面,就可以使用桌面路径来指定文件的位置。 2、调试信息:在开发过程中,我们往往会将一些调试…...
基于SSM的考研图书电子商务平台的设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

信息系统“好用”的标准探讨
数字化转型建设的关键不在建设信息系统。这是为了避免走信息化建设的老路——业务和信息化两张皮,寄希望信息系统解决业务问题。在数字化转型建设中,信息系统仍然是重要抓手和显性成果,是企业业务和数据的承载平台,也是IT厂商向客…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
