c语言练习第11周(1~5)
数列 1 1 2 3 5 8 13 21 ... 被称为斐波纳数列。
输入若干个正整数N,输出这个序列的前 N 项的和。
| 题干 | 数列 1 1 2 3 5 8 13 21 ... 被称为斐波纳数列。 输入若干个正整数N,输出这个序列的前 N 项的和。 | ||
| 输入样例 | 3 5 4 1 | ||
| 输出样例 | 4 12 7 1 | ||
#include<stdio.h>
int fbnq(int n) {int i = 1, a = 1, b = 1,c,s=0;for (i = 1; i <= n; i++) {s += a;c = a + b;a = b;b = c;}return s;
}
int main() {int n;while (~scanf("%d", &n)) {printf("%d\n", fbnq(n));}return 0;
}
数列 0 1 1 2 3 5 8 13 21 ... 被称为斐波纳数列。
输入若干个正整数N,输出这个序列的前 N 项。
| 题干 | 数列 0 1 1 2 3 5 8 13 21 ... 被称为斐波纳数列。 输入若干个正整数N,输出这个序列的前 N 项。 | ||
| 输入样例 | 3 5 1 4 | ||
| 输出样例 | 0,1,1, 0,1,1,2,3, 0, 0,1,1,2, | ||
#include<stdio.h>
int fbnq(int n) {int i = 1, a = 0, b = 1,c,s=0;for (i = 1; i <= n; i++) {printf("%d,",a);c = a + b;a = b;b = c;}return s;
}
int main() {int n;while (~scanf("%d", &n)) {fbnq(n);printf("\n");}return 0;
}a数组n个元素插入法升序排序,请补充代码。
| 题干 | a数组n个元素插入法升序排序,请补充代码。 void fun(int a[],int n) { int i,j,t; for(i=1;i<=n-1;i++) { t=a[i]; /****************/ /****************/ a[j+1]=t; } } | ||
//只填写两行/****/之间要求的语句列表
for(j=i-1;j>=0;j--)if(a[j]>t)a[j+1]=a[j];else break; 输入一个二维数组 M[12][12],根据输入要求,求出二维数组下方绿色部分元素的平均值或和。
第一行输入一大写字母,若为 S,则求和,若为 M,则求平均值。
接下来 12 行,每行包含 12 个用空格隔开的浮点数,输出结果保留一位小数。
数据范围:100.0≤M[i][j]≤100.0。
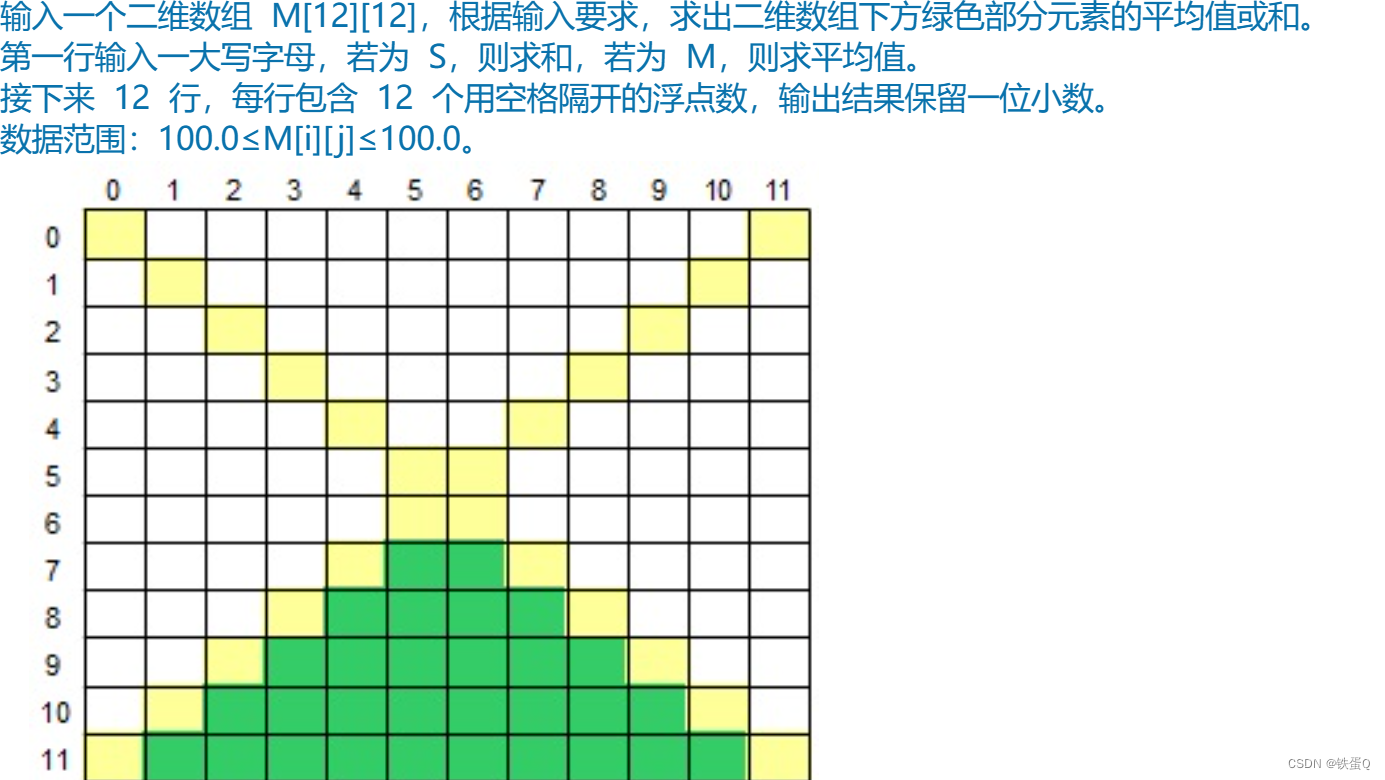
| 输入样例 | S -6.0 0.7 -8.4 -5.7 -4.1 7.6 9.5 -9.7 4.1 0.6 -6.5 -4.9 6.6 4.9 -3.1 5.3 0.3 -4.5 3.9 -1.5 6.6 7.0 5.1 2.5 -8.5 1.8 -2.7 0.1 -4.9 -7.2 4.3 6.0 -1.4 2.7 -3.0 2.0 4.8 -7.0 -1.3 0.8 1.0 4.5 -1.1 -2.9 -3.9 -3.9 -8.9 5.8 -2.1 -9.6 5.1 0.2 1.0 -1.7 6.4 4.1 2.8 -6.9 2.4 9.3 -6.0 -9.1 -7.0 -7.0 7.8 5.1 6.9 -7.6 0.4 -7.2 5.5 6.0 -1.9 5.5 1.9 -8.5 -5.3 2.3 -9.3 2.0 -0.2 1.2 5.6 -1.8 8.2 2.3 3.5 1.4 4.0 -5.1 -6.9 -2.8 1.7 -7.0 7.8 1.8 -6.0 -4.1 -4.6 -9.4 -4.9 -4.1 4.2 6.3 -2.8 8.7 8.1 -0.9 8.8 -6.5 -4.3 6.1 -6.2 -3.9 -7.0 7.3 5.0 -0.9 -0.0 5.6 -2.4 1.4 8.5 -2.2 0.9 5.3 3.6 8.8 -8.1 3.0 -3.1 6.5 -3.8 -6.4 2.3 4.2 -9.8 -0.3 -9.9 -7.4 3.5 1.5 -0.2 7.0 | ||
| 输出样例 | -11.9 | ||
#include<stdio.h>
int main() {int n = 0, i, j;char c;scanf("%c", &c);double M[12][12],s=0;for (i = 0; i < 12; i++) {for (j = 0; j < 12; j++) {scanf("%lf", &M[i][j]);if (i + j > 11 && j<i) {s += M[i][j];n++;}}}if (c == 'S') {printf("%.1lf\n", s);}else {printf("%.1lf\n", s/n);}return 0;
}
输入一个二维数组 M[12][12],根据输入要求,求出二维数组左方绿色部分元素的平均值或和。
第一行输入一大写字母,若为 S,则求和,若为 M,则求平均值。
接下来 12 行,每行包含 12 个用空格隔开的浮点数,输出结果保留一位小数。
数据范围:100.0≤M[i][j]≤100.0。

#include<stdio.h>
int main() {int n = 0, i, j;char c;scanf("%c", &c);double M[12][12], s = 0;for (i = 0; i < 12; i++) {for (j = 0; j < 12; j++) {scanf("%lf", &M[i][j]);if (i + j < 11 && j < i) {s += M[i][j];n++;}}}if (c == 'S') {printf("%.1lf\n", s);}else {printf("%.1lf\n", s / n);}return 0;
}
相关文章:

c语言练习第11周(1~5)
数列 1 1 2 3 5 8 13 21 ... 被称为斐波纳数列。 输入若干个正整数N,输出这个序列的前 N 项的和。 题干数列 1 1 2 3 5 8 13 21 ... 被称为斐波纳数列。 输入若干个正整数N,输出这个序列的前 N 项的和。输入样例3 5 4 1输出样例…...

阿里云国际站服务器如何升级内存容量?
阿里云服务器是阿里云供给的计算服务,它具有高效安稳、可扩展性强等特色,适用于各种应用环境。在运用阿里云服务器的过程中,或许会遇到内存容量缺乏的状况,这时候就需求晋级内存容量。那么,阿里云服务器怎么晋级内存容…...
神经网络(第二周)
一、简介 1.1 需求预测示例 1.1.1 逻辑回归算法 根据价格预测商品是否畅销。特征:T恤的价格;分类:销售量高1/销售量低0;使用逻辑回归算法进行分类,拟合效果如下图所示: 1.1.2 神经元和神经网络 将逻辑回…...
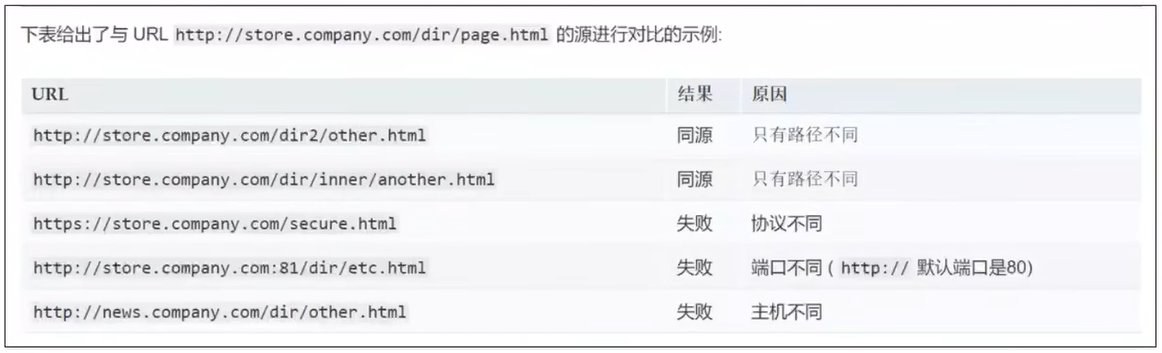
《网络协议》04. 应用层(DNS DHCP HTTP)
title: 《网络协议》04. 应用层(DNS & DHCP & HTTP) date: 2022-09-05 14:28:22 updated: 2023-11-12 06:55:52 categories: 学习记录:网络协议 excerpt: 应用层、DNS、DHCP、HTTP(URI & URL,ABNF…...

springboot自己添加的配置文件没有绿色叶子问题
在IntelliJ IDEA中,不同文件类型通常会有不同的图标,以便更容易识别它们。如果您的自己添加的 .properties 文件和项目中自动生成的 .properties 文件显示不同的图标,这可能是因为它们被识别为不同的文件类型。 通常情况下,Intel…...
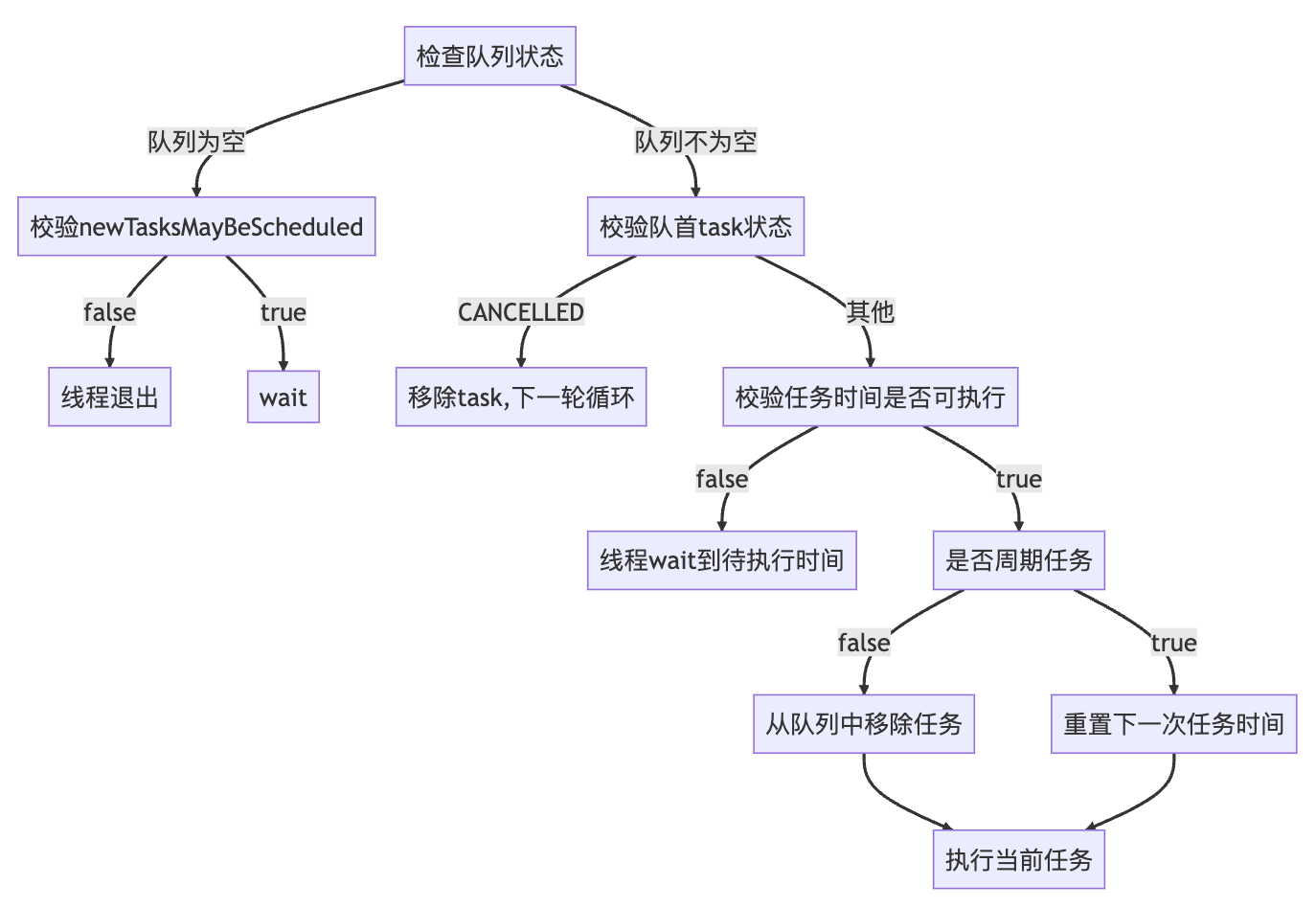
【Java】定时任务 - Timer/TimerTask 源码原理解析
一、背景及使用 日常实现各种服务端系统时,我们一定会有一些定时任务的需求。比如会议提前半小时自动提醒,异步任务定时/周期执行等。那么如何去实现这样的一个定时任务系统呢? Java JDK提供的Timer类就是一个很好的工具,通过简单…...

SAP ABAP基础语法-Excel上传(十)
EXCEL BDS模板上传及赋值 上传模板事务代码:OAER l 功能代码:向EXCEL模板中写入数据示例代码如下 REPORT ZEXCEL_DOI. “doi type pools TYPE-POOLS: soi. *SAP Desktop Office Integration Interfaces DATA: container TYPE REF TO cl_gui_custom_c…...
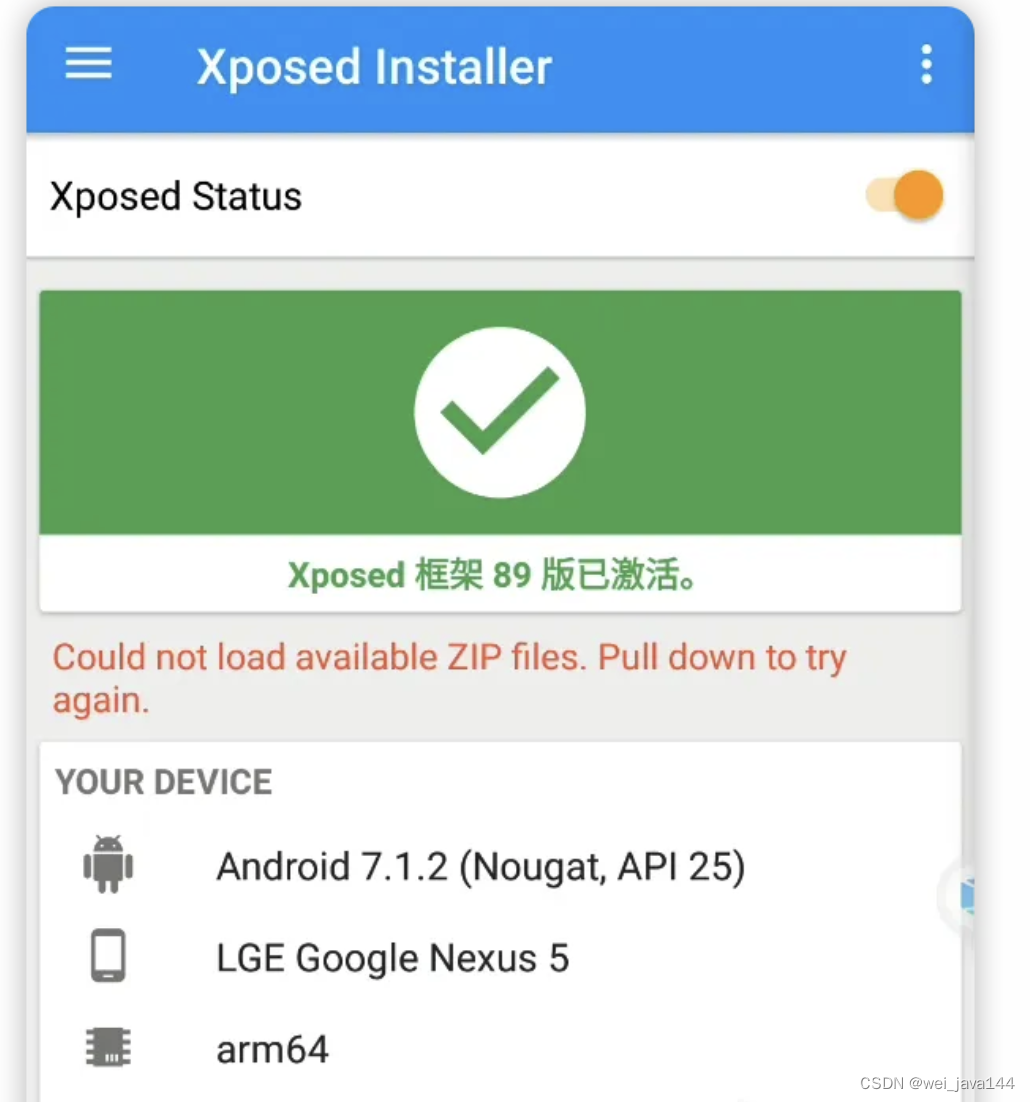
记录一次某某虚拟机的逆向
导语 学了一段时间的XPosed,发现XPosed真的好强,只要技术强,什么操作都能实现... 这次主要记录一下我对这款应用的逆向思路 apk检查 使用MT管理器检查apk的加壳情况 发现是某数字的免费版本 直接使用frida-dexdump 脱下来后备用 应用分…...
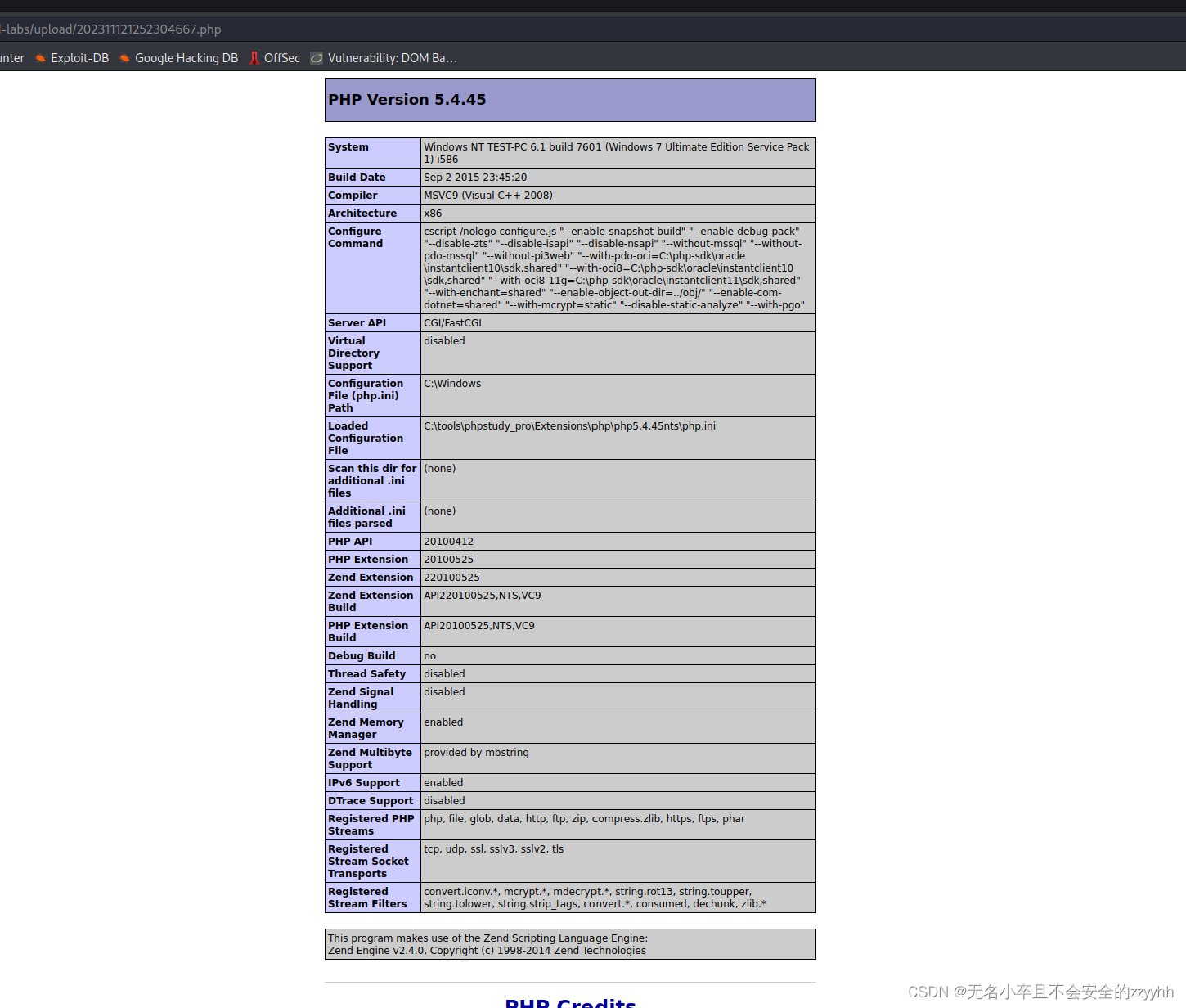
upload-labs关卡7(基于黑名单的空格绕过)通关思路
文章目录 前言一、回顾上一关知识点二、靶场第七关通关思路1、看源代码2、空格绕过3、检查文件是否成功上传 总结 前言 此文章只用于学习和反思巩固文件上传漏洞知识,禁止用于做非法攻击。注意靶场是可以练习的平台,不能随意去尚未授权的网站做渗透测试…...

CnosDB 在最近新发布的 2.4.0 版本中增加对时空函数的支持。
CnosDB 在最近新发布的 2.4.0 版本中增加对时空函数的支持。 概述 时空函数是一种用于描述时空结构和演化的函数。它在物理学、数学和计算机科学等领域中都有广泛的应用。时空函数可以描述物体在时空中的位置、速度、加速度以及其他相关属性。 用法 CnosDB 将使用一种全新的…...

python实现炒股自动化,个人账户无门槛量化交易的开始
本篇作为系列教程的引子,对股票量化程序化自动交易感兴趣的朋友可以关注我,现在只是个粗略计划,后续会根据需要重新调整,并陆续添加内容。 股票量化程序化自动交易接口 很多人在找股票个人账户实现程序化自动交易的接口࿰…...

推荐系统笔记--Swing模型的原理
1--Swing模型的引入 在 Item CF 召回中,物品的相似度是基于其受众的交集来衡量的,但当受众的交集局限在一个小圈子时,就会误将两个不相似的物品定义为相似; Swing 模型引入用户的重合度来判断两个用户是否属于一个小圈子ÿ…...
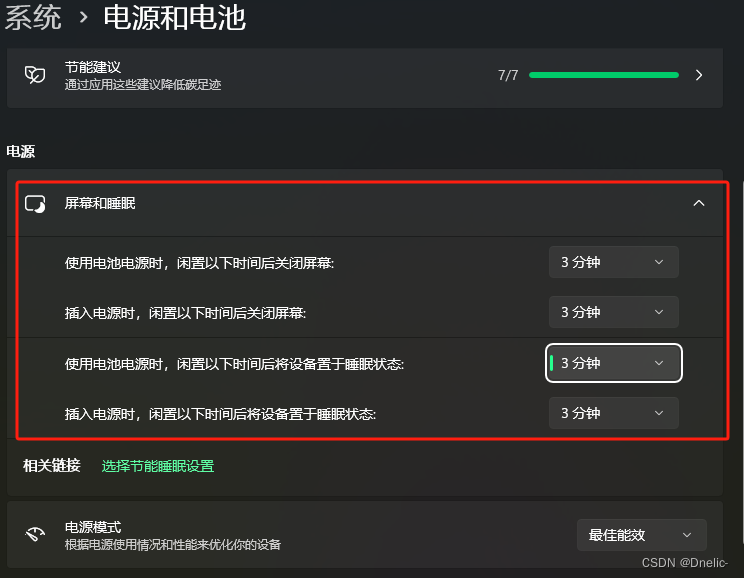
联想小新Pro14默认设置的问题
联想小新Pro14 锐龙版,Win11真的挺多不习惯的,默认配置都不符合一般使用习惯。 1、默认人走过自动开机。人机互动太强了; 2、默认短超时息屏但不锁屏,这体验很容易觉得卡机然后唤起,却又不用密码打开; 3…...
)
【洛谷 P5019】[NOIP2018 提高组] 铺设道路 题解(分治算法+双指针)
[NOIP2018 提高组] 铺设道路 题目背景 NOIP2018 提高组 D1T1 题目描述 春春是一名道路工程师,负责铺设一条长度为 n n n 的道路。 铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 n n n 块首尾相连的区域,一开始,第 i i i …...

牛客刷题记录11.12
继承和组合 二进制数统计 1的个数 和 0 的个数...
NextJS开发:使用IconPark、Lucide图标库
IconPark、Lucide两个很不错的图标库,如果需要用到微信、阿里等国内logo可以使用IconPark,Lucide中没有包含这些内容。 安装IconPark npm install icon-park/react --save简单使用 import {Home} from icon-park/react;<Home/> <Home theme&…...
11.12总结
这一周主要写了个人中心的几个功能,资料修改,收货地址的创建和修改删除,还有主页界面和商品界面...

Gogs安装和部署教程-centos上
0、什么是 Gogs? Gogs 是一款极易搭建的自助 Git 服务。 Gogs 的目标是打造一个最简单、最快速和最轻松的方式搭建自助 Git 服务。使用 Go 语言开发使得 Gogs 能够通过独立的二进制分发,并且支持 Go 语言支持的 所有平台,包括 Linux、Mac OS X、Windo…...

Unity中Shader雾效的实现方法一
文章目录 前言一、在片元着色器中使用如下公式计算最终的颜色 lerp(雾效颜色,物体颜色,雾效混合因子)1、获取雾效颜色2、物体的颜色一般通过纹理采样得到,此处用 1 代替测试3、获取 雾效混合因子(由 雾的距离 和 雾的浓度决定&am…...
Mac安装配置Tomcat,以及使用(详解)
目录 一、Tomcat下载: 1、左栏选择Tomcat版本 2、点击下载即可,任选其一 编辑3、下载好的文件夹放到用户名下即可(之前已经下载过,这里以Tomcat 8.5.88为演示),这里提供8.5.88的安装包: 二…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...
