力扣第647题 回文子串 c++ 动态规划 双指针 附Java代码 注释解释版
题目
647. 回文子串
中等
相关标签
字符串 动态规划
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:s = "abc" 输出:3 解释:三个回文子串: "a", "b", "c"
示例 2:
输入:s = "aaa" 输出:6 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
提示:
1 <= s.length <= 1000s由小写英文字母组成
思路和解题方法 一 动态规划
vector<vector<bool>> dp(s.size(),vector<bool>(s.size(),false));:这行代码定义了一个二维布尔类型的动态规划数组dp,用来记录字符串s中从位置i到j的子串是否为回文串。
int ans = 0;:初始化一个变量ans用来存储回文子串的数量。
for(int i = s.size()-1;i>=0;i--):从字符串的末尾向前遍历每个字符,作为子串的起始位置。
for(int j = i;j<s.size();j++):遍历以当前i位置字符为起始的所有可能的子串。
if(s[i] == s[j] && (j-i<=1||dp[i+1][j-1])):如果当前子串的两端字符相同,并且长度不超过1,或者去掉两端字符后剩下的子串是回文串(根据dp数组的记录),则认为当前子串是回文串。
ans++;:累加回文子串的数量。
dp[i][j] = true;:更新dp数组,表示从位置i到j的子串是回文串。最后返回ans,即为字符串s中回文子串的数量。
复杂度
时间复杂度:
O(n*n)
时间复杂度为O(n^2),其中n为输入字符串s的长度。这是因为代码中使用了两重循环来遍历所有可能的子串,并在每次循环中进行常数时间的比较和更新操作。
空间复杂度
O(n*n)
至于空间复杂度,由于使用了一个二维动态规划数组dp,其大小为s.size() * s.size(),因此空间复杂度也为O(n^2)。
c++ 代码 1
打印的dp数组:(以“abcba"为样例)
a b c b a

class Solution {
public:int countSubstrings(string s) {// 创建一个二维动态规划数组dp,用于记录子串是否为回文vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int ans = 0; // 记录回文子串的数量for (int i = s.size() - 1; i >= 0; i--) {for (int j = i; j < s.size(); j++) {// 如果当前字符相等,并且满足回文条件,则更新结果和dp数组if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])) {ans++; // 回文子串数量加一dp[i][j] = true; // 更新dp数组表示从i到j的子串是回文}}}return ans; // 返回回文子串的数量}
};
双指针
先看时间空间复杂度对比:(大差不差的区别)
以下是双指针法
思路和解题方法 二 双指针
主函数
countSubstrings中,首先初始化变量ans为0,用于存储回文子串的数量。然后通过一个for循环遍历字符串
s的每个字符(下标为i),对于每个字符,分别调用explore函数两次:
- 第一次调用
explore(s, i, i, s.size()):以当前字符为中心,向两边扩展寻找回文子串。- 第二次调用
explore(s, i, i+1, s.size()):以当前字符和下一个字符为中心,向两边扩展寻找回文子串。在
explore函数中,通过双指针i和j向两边扩展,检查以i和j为中心的回文子串数量。当i和j位置的字符相等时,i向左移动,j向右移动,并同时增加回文子串数量
cnt。最后返回
cnt作为以i和j为中心的回文子串数量。最后,主函数返回累加的回文子串数量
ans。
复杂度
时间复杂度:
O(n*n)
时间复杂度为O(n^2),其中n为输入字符串s的长度。这是因为在主函数
countSubstrings中,通过一个嵌套的循环遍历字符串s的每个字符,并且在explore函数中,利用双指针向两边扩展来判断回文子串,最坏情况下需要O(n)的时间复杂度。
空间复杂度
O(1)
空间复杂度则为O(1),因为除了存储回文子串数量的变量
ans外,算法并未使用额外的空间,因此空间复杂度是常数级的。
c++ 代码 2
class Solution {
public:int countSubstrings(string s) {int ans = 0; // 初始化回文子串数量为0for(int i = 0; i < s.size(); i++) { // 遍历字符串s的每个字符ans += explore(s, i, i, s.size()); // 以当前字符为中心,向两边扩展寻找回文子串ans += explore(s, i, i + 1, s.size()); // 以当前字符和下一个字符为中心,向两边扩展寻找回文子串}return ans; // 返回回文子串的总数量}int explore(const string &s, int i, int j, int n) {int cnt = 0; // 记录以i和j为中心的回文子串数量while(i >= 0 && j < n && s[i] == s[j]) { // 向两边扩展,直到不是回文串为止i--; // 向左移动指针j++; // 向右移动指针cnt++; // 回文子串数量加一}return cnt; // 返回回文子串数量}
};
附Java代码
1.动态规划
class Solution {public int countSubstrings(String s) {// 创建一个二维数组dp,dp[i][j]表示从索引i到索引j的子串是否为回文子串boolean[][] dp = new boolean[s.length()][s.length()];int res = 0; // 用于存储回文子串数量的变量// 双重循环遍历字符串,i表示起始索引,j表示结束索引for (int i = s.length() - 1; i >= 0; i--) {for (int j = i; j < s.length(); j++) {// 如果当前字符相等,并且满足以下条件之一:// 1. j和i相差不超过1,即长度为1或2的子串// 2. dp[i+1][j-1]为true,即去掉头尾字符后的子串是回文串if (s.charAt(i) == s.charAt(j) && (j - i <= 1 || dp[i + 1][j - 1])) {res++; // 回文子串数量加1dp[i][j] = true; // 标记索引i到索引j的子串为回文子串}}}return res; // 返回回文子串数量}
}
2.双指针
class Solution {public int countSubstrings(String s) {int len, ans = 0; // 初始化变量len和ansif (s == null || (len = s.length()) < 1) return 0; // 如果输入字符串为空或长度小于1,则直接返回0// 总共有2 * len - 1个中心点,因为可以以每个字符为中心,也可以以两个字符之间的空隙为中心for (int i = 0; i < 2 * len - 1; i++) {// 通过遍历每个回文中心,向两边扩散,并判断是否回文子串// 有两种情况,当i为偶数时,回文中心是一个字符;当i为奇数时,回文中心是两个字符之间的空隙int left = i / 2, right = left + i % 2; // 根据i的奇偶性确定回文中心的左右位置while (left >= 0 && right < len && s.charAt(left) == s.charAt(right)) {// 如果当前是一个回文子串,则记录数量ans++;left--;right++;}}return ans; // 返回回文子串数量}
}
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:

力扣第647题 回文子串 c++ 动态规划 双指针 附Java代码 注释解释版
题目 647. 回文子串 中等 相关标签 字符串 动态规划 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串…...
【Go入门】struct类型
【Go入门】struct类型 struct Go语言中,也和C或者其他语言一样,我们可以声明新的类型,作为其它类型的属性或字段的容器。例如,我们可以创建一个自定义类型person代表一个人的实体。这个实体拥有属性:姓名和年龄。这样…...

怎么改变容易紧张的性格?
容易紧张的性格是比较通俗的说法,在艾森克人格测试中,容易紧张的性格就属于神经症人格,神经质不是神-经-病,而是一种人格特征,这种特征包括:敏感,情绪不稳定,易焦虑和紧张。有兴趣的…...

合作共赢 共克时艰
采访人:最近财政部11月6日通报隐性债务问责典型案例,这中间涉及湖北多所重要地市,形成新增隐性债务200多亿,您怎么看这件事? 辜渝傧:是的,无论是数字还是涉及的范围都可以明显感觉到“防范…...

VCSA7许可证过期问题
公司两台ESXI7虚拟化系统,使用VCSA7进行日常管理,在使用过程中一直清单中包含过期或即将过期的许可证。 查看许可证清单中,已经添加了正式授权的许可证,且已经分配给了ESXI主机,但是任然有到期提示。 最后查看试用许可…...
解决win11更新后,文件夹打不开的bug
更新win11系统了,给我更了个bug,找了好多解决方案,发现下面这个可以解决问题。 第一步 找到注册表 第二步 备份注册表 为了防止意外情况,备份注册表。如有意外问题,可以导入导出的注册表进行恢复。 第三步 删除指定…...
修复了数个Bug!
v2.0.1版本已经在 github release 了,欢迎大家体验使用,开源版是永久免费的。 ## 新增与优化的功能 新增(测试报告): 测试报告根据测试执行详情,进行查看 新增(用户设置): 用户权限为普通用户和管理员,普通用户根据设置的默认产品…...
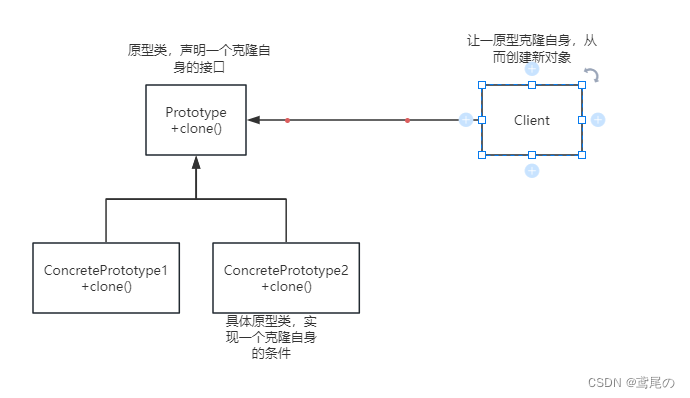
设计模式之--原型模式(深浅拷贝)
原型模式 缘起 某天,小明的Leader找到小明:“小明啊,如果有个发简历的需求,就是有个简历的模板,然后打印很多份,要去一份一份展示出来,用编程怎么实现呢?” 小明一听,脑袋里就有了…...

Linux服务器从零开始训练 RT-DETR 改进项目 (Ultralytics) 教程,改进RTDETR算法(包括使用训练、验证、推理教程)
手把手从零开始训练 RT-DETR 改进项目 (Ultralytics版本) 教程,改进RTDETR算法 本文以Linux服务器为例:从零开始使用Linux训练 RT-DETR 算法项目 《芒果剑指 RT-DETR 目标检测算法 改进》 适用于芒果专栏改进RT-DETR算法 文章目录 百度 RT-DETR 算法介绍改进网络代码汇总第…...

矩阵理论--矩阵分解
矩阵理论–矩阵分解 矩阵的三角分解、谱分解、最大秩分解、奇异值分解的操作步骤,以及相关说明。 1、QR分解 (1)非奇异方阵 方阵(非奇异):将方阵分解成酉矩阵左乘正线上三角,或者酉矩阵右乘…...

go语言相关bug
第一个bug itcastitcast:/home/jian/share/src/go-test/homeweb-client$ go mod tidy go: finding module for package github.com/micro/go-grpc go: found github.com/micro/go-grpc in github.com/micro/go-grpc v1.0.1 go: homeweb-client/handler importsgithub.com/micr…...

Spring Cloud OpenFeign:基于Ribbon和Hystrix的声明式服务调用
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! Spring Cloud OpenFeign:基于Ribbon和Hystrix的声明式服务调用 Spring Cloud OpenFeign是一个声明式的服务调用框架,基于Feign并整合了Ribbon和…...

租用服务器带宽类型应用
服务器带宽类型多样,以满足不同行业的需求。本文将介绍香港常见的服务器带宽类型及其应用领域。 1. 共享带宽 共享带宽是指多个用户共同使用同一台服务器的带宽资源。这种带宽类型适用于小型企业或个人网站,因为其成本较低。由于多个用户共享带宽资源&…...
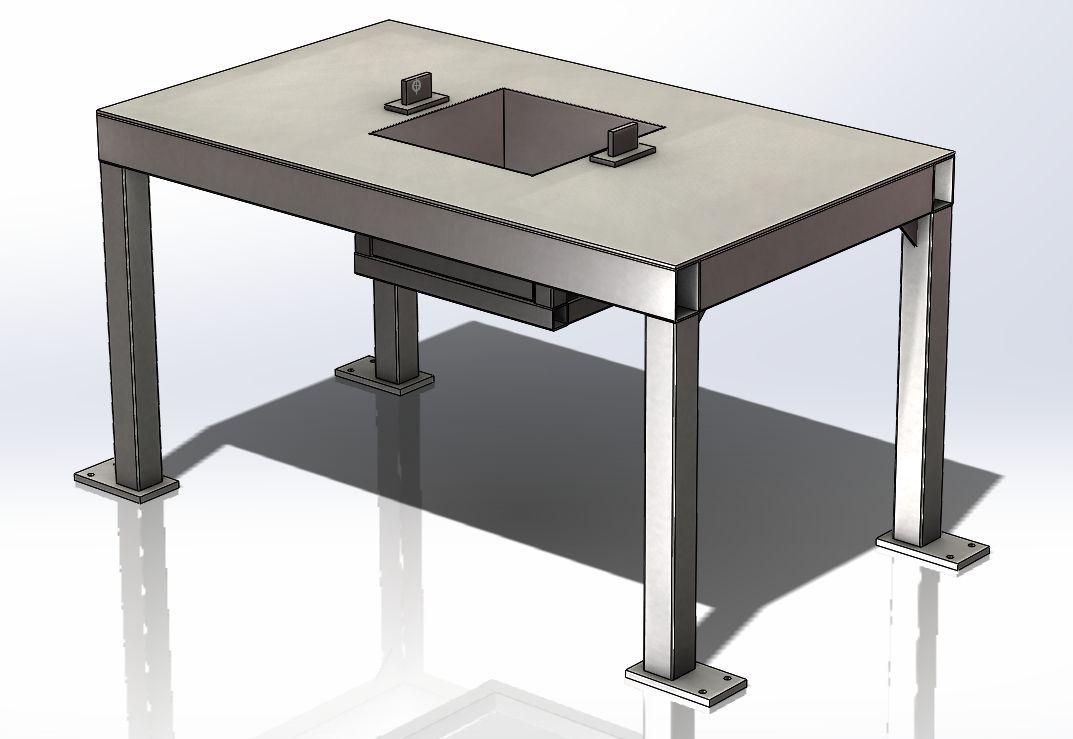
SOLIDWORKS实用技巧之焊件轮廓应用
1.焊件轮廓库官方下载入口 焊件轮廓可以自制,也可以从软件中在线下载获取直接使用,如图1,联网状态按ctrl左键点击下载,解压后获得库文件。 图1 图2 2.库放置的位置和配置 从SOLIDWORKS2014版起,软件焊件轮廓库支持可…...

本地浏览器全局翻译 demo 以火狐firefox为例【免费-简单】
translateDemo 介绍使用说明简单到流泪 本地浏览器全局翻译 demo 以火狐firefox为例 1、安装插件 使用少量的 JavaScript 脚本,自由定义网页显示与运行方式。2、将上述脚本 追加到 插件中即可实现全局翻译;3、免费;参与贡献特技 translateDe…...

使用多线程处理List数据
最近遇到了一个业务场景,需要对List中的数据逐个发起http请求(List中的数据各自独立,对执行顺序无要求),考虑到可以使用多线程加快处理速度。 封装了如下方法: /// <summary>/// 多线程处理数据-无返回值/// </summary&…...

Elasticsearch--Python使用、Django/Flask集成
一、Python使用 from elasticsearch import Elasticsearchobj Elasticsearch() # 创建索引(Index) result obj.indices.create(indexuser, body{"userid":1,username:lqz},ignore400) # print(result) # 删除索引 # result obj.indices.de…...
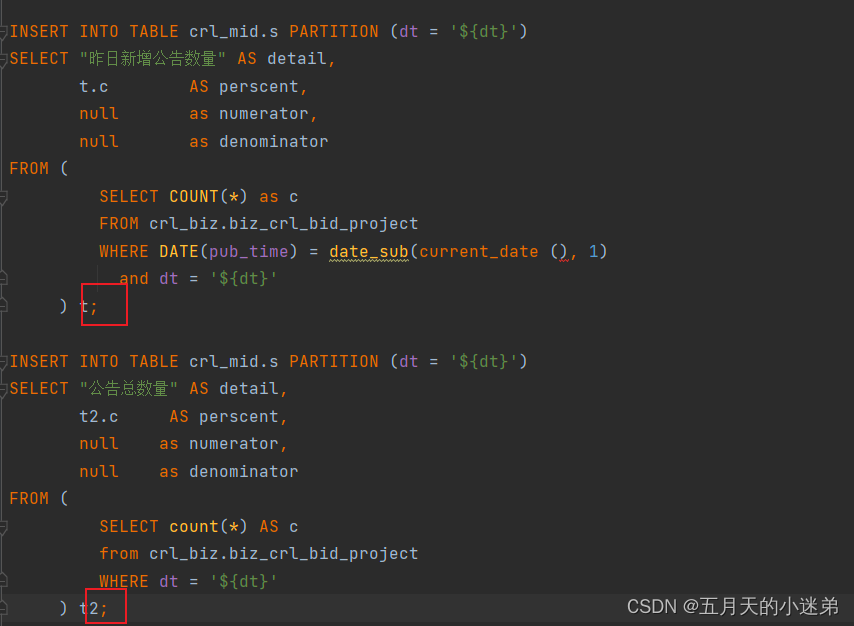
pyspark将数据多次插入表的时候报错
代码 报错信息 py4j.protocol.Py4JJavaError: An error occurred while calling o129.sql. : org.apache.spark.sql.catalyst.parser.ParseException: mismatched input INSERT expecting <EOF>(line 12, pos 0) 原因 插入语句结束后没有加;结尾 把两个&am…...

Qt绘制饼状图
必须在MainWindow.h头文件开头放 #include <QtCharts> //必须这么设置 创建chart: void MainWindow::iniPiewChart() { //饼图初始化QChart *chart new QChart();chart->setTitle(" Piechart演示");chart->setAnimationOptions(QChar…...
Vue3 setup函数
一、setup函数介绍 setup函数是Vue3中全新的一个配置项,值为一个函数,是所有 Composition API 中“表演的舞台”。 我们在Vue2中用到的所有数据、方法,都需要配置在setup中。 这是我们在Vue2中的写法: 这是我们在Vue3 setup中的…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
