矩阵理论--矩阵分解
矩阵理论–矩阵分解
矩阵的三角分解、谱分解、最大秩分解、奇异值分解的操作步骤,以及相关说明。
1、QR分解
(1)非奇异方阵
方阵(非奇异):将方阵分解成酉矩阵左乘正线上三角,或者酉矩阵右乘正线下三角。
- 分解步骤:
- 列分块得n个列向量构成的向量组;
- 将n个列向量施密特正交单位化;
- 用标准正交基表出该向量组;
- 写成矩阵相乘的形式,即得三角分解。
- 施密特正交化-单位化:
- B1 = A1/|A1|;
- B2 = [A2-(A2,B1)B1]/|A2-(A2,B1)|;
- B3 = [A3 - (A3,B2)B2-(A3,B1)B1]/|A3 - (A3,B2)B2-(A3,B1)B1|;
- 反过来表出:记k11=|A1|,k22 = |A2-(A2,B1)|,k12=(B1,A2)
- A1 = k11B1;
- A2 = k12B1+k22B2;
- A3 = k13B1+k23B2+k33B3;
- A = [A1,A2,A3] = [B1,B2,B3][k11,k12,k13; 0,k22,k23;0,0,k33]
(2)满秩的高矩阵、宽矩阵
- 列满秩矩阵,列分块,添加列向量,补成一个方阵(非奇异),再按方阵的方式分解,将得到一个方形的酉矩阵左乘(正线上三角;0)
- 行满秩矩阵,行分块,添加行向量,补成一个方阵(非奇异),再按方阵的方式分解,将得到一个方形的酉矩阵右乘(正线下三角,0)
(3)其它矩阵
奇异矩阵,非满秩的高矩阵、宽矩阵,可以分解为 U ∣ L 0 0 0 ∣ V U\begin{vmatrix}L&0\\0&0\end{vmatrix}V U L000 V,U、V是两个方形酉矩阵(不一定同阶)。
分解步骤
2、谱分解
谱是指矩阵的所有特征根构成的集合,表示为 𝜆(A)={𝜆1,𝜆2,……,𝜆r}。
首先需要指出,只有单纯矩阵才有谱分解。
(1)单纯矩阵:每个特征根的基础解系的维数等于特征根的重数。
单纯矩阵,等价于可对角化矩阵。
- 分解步骤:P仅是一个非奇异阵。
- 解特征方程式,求特征根;
- 相似对角化:D = diag() = P-1AP;A = PDP-1;
- P列分块,P-1行分块,利用分块矩阵的乘法即得A的谱分解
- 单纯矩阵谱分解就是将矩阵分解成一系列的秩一矩阵加权和。
- 相似对角化:
- Ap = p𝜆,p是某个特征根的特征向量
- 由于是单纯矩阵,该特征根有几重,这样的p就有几个,这几个p要求线性无关;
- 一共有n个p,从而构成一个方阵P,且线性无关,那么就非奇异,有逆;
- D = P-1AP。
- 秩一矩阵:行向量乘以列向量。
- 幂等矩阵:投影矩阵,AA=A;由于P-1P=E,则P的行向量乘以P-1的列向量,将得到一个幂等矩阵。
- 幂等矩阵的秩可以是小于n的任何一个数,0矩阵也是一种幂等矩阵;特征值非零即1,可对角化。
- 秩一矩阵要么是幂等矩阵,要么是幂等矩阵乘以一个缩放因子,即AA=kA。
(2)正规矩阵:满足AHA=AAH。正规矩阵一定是单纯矩阵。
-
分解步骤:此处的P是一个酉矩阵。
- 相似对角化;
- P列分块,P-1行分块,分块矩阵乘法。
-
正规矩阵谱分解成了一系列的正交投影的加权和。
-
正交投影:幂等矩阵,并且是Hermite阵。
-
如果A为上三角矩阵,则A是正规矩阵的充要条件是A为对角矩阵;
-
如果A为块上三角矩阵,则A是正规矩阵的充要条件是A为块对角矩阵,且对角块为正规矩阵。
-
tr(AAH)=tr(AHA)=A的矩阵二范数;
3、最大秩分解
- 最大秩分解:任意矩阵A,A=BD,B是一个列满秩矩阵,D是一个行满秩矩阵,三个矩阵的秩相等。
- 分解方法:
- A化为行简化阶梯形A_w;
- A_w的非0列对应于A中的列构成B,A_w的非0行对应于A_w的行构成D
- 列满秩矩阵:A是mxn的矩阵,若m>=n,则rank(A)<=n,nullity(A)<=n
- 秩零度定理:rank(A) + nullity(A) = n
- nullity(A)等于Ax=0的解空间维数。
- 如果rank(A)=n,那么nullity(A)=0,即Ax=0的解空间为零空间。
- 列满秩矩阵构成的齐次线性方程组只有零解。
4、奇异值分解
三角分解: A = U ∣ L 0 0 0 ∣ V A=U\begin{vmatrix}L&0\\0&0\end{vmatrix}V A=U L000 V
其中L是一个r阶正线下三角矩阵。
为了进一步简化,发展出奇异值分解: A = U ∣ D 0 0 0 ∣ V A=U\begin{vmatrix}D&0\\0&0\end{vmatrix}V A=U D000 V。
其中D是一个r阶正线对角矩阵。
- 分解步骤:
- 求AHA的特征值,从而求出正奇异值 σ i = λ i \sigma_i = \sqrt{\lambda_i} σi=λi。
- 由于是正规矩阵,因此可以将每个特征根对应的特征子空间的基抽出来构成一个n阶酉矩阵 V = ∣ V 1 V 2 ∣ V = \begin{vmatrix}V1\\V2 \end{vmatrix} V= V1V2 。
- A H A = V H ∣ D H D 0 0 0 ∣ V A^HA=V^H\begin{vmatrix}D^HD&0\\0&0\end{vmatrix}V AHA=VH DHD000 V
- D H D = d i a g { λ 1 , λ 2 , . . . , λ r } D^HD=diag\{{\lambda_1,\lambda_2,...,\lambda_r}\} DHD=diag{λ1,λ2,...,λr};D=diag{𝛿1,𝛿2,…,𝛿r},|𝛿i| = 𝛔i > 0; D的取法不唯一,𝛿i是一个复数,模长为𝛔i,相位任意。
- U = (U1, U2);U1 = AV1HD-1;U2是U1的正交补,U2HU1=0。U1Hx=0,求出基础解系,U1和基础解系一起作施密特正交化,即得U。
- UHAVH = ∣ D 0 0 0 ∣ \begin{vmatrix}D&0\\0&0\end{vmatrix} D000 ;
- A = U ∣ D 0 0 0 ∣ V U\begin{vmatrix}D&0\\0&0\end{vmatrix}V U D000 V
- (AHA)H = AHA,因此AHA是n阶正规矩阵,正规矩阵可以谱分解成一系列正交投影的加权和,正规矩阵是半正定矩阵。
- 正交补的求法:W2是W1的正交补。
- 根据秩零度定理:rank(A)+N(A)=n;
- A的极大无关列向量组可张成rank(A)维的空间W1;
- 令Ax=0,求出基础解系,基础解系可张成解空间W2;
- W1⨁W2=V(Cn)
相关文章:

矩阵理论--矩阵分解
矩阵理论–矩阵分解 矩阵的三角分解、谱分解、最大秩分解、奇异值分解的操作步骤,以及相关说明。 1、QR分解 (1)非奇异方阵 方阵(非奇异):将方阵分解成酉矩阵左乘正线上三角,或者酉矩阵右乘…...

go语言相关bug
第一个bug itcastitcast:/home/jian/share/src/go-test/homeweb-client$ go mod tidy go: finding module for package github.com/micro/go-grpc go: found github.com/micro/go-grpc in github.com/micro/go-grpc v1.0.1 go: homeweb-client/handler importsgithub.com/micr…...

Spring Cloud OpenFeign:基于Ribbon和Hystrix的声明式服务调用
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! Spring Cloud OpenFeign:基于Ribbon和Hystrix的声明式服务调用 Spring Cloud OpenFeign是一个声明式的服务调用框架,基于Feign并整合了Ribbon和…...

租用服务器带宽类型应用
服务器带宽类型多样,以满足不同行业的需求。本文将介绍香港常见的服务器带宽类型及其应用领域。 1. 共享带宽 共享带宽是指多个用户共同使用同一台服务器的带宽资源。这种带宽类型适用于小型企业或个人网站,因为其成本较低。由于多个用户共享带宽资源&…...
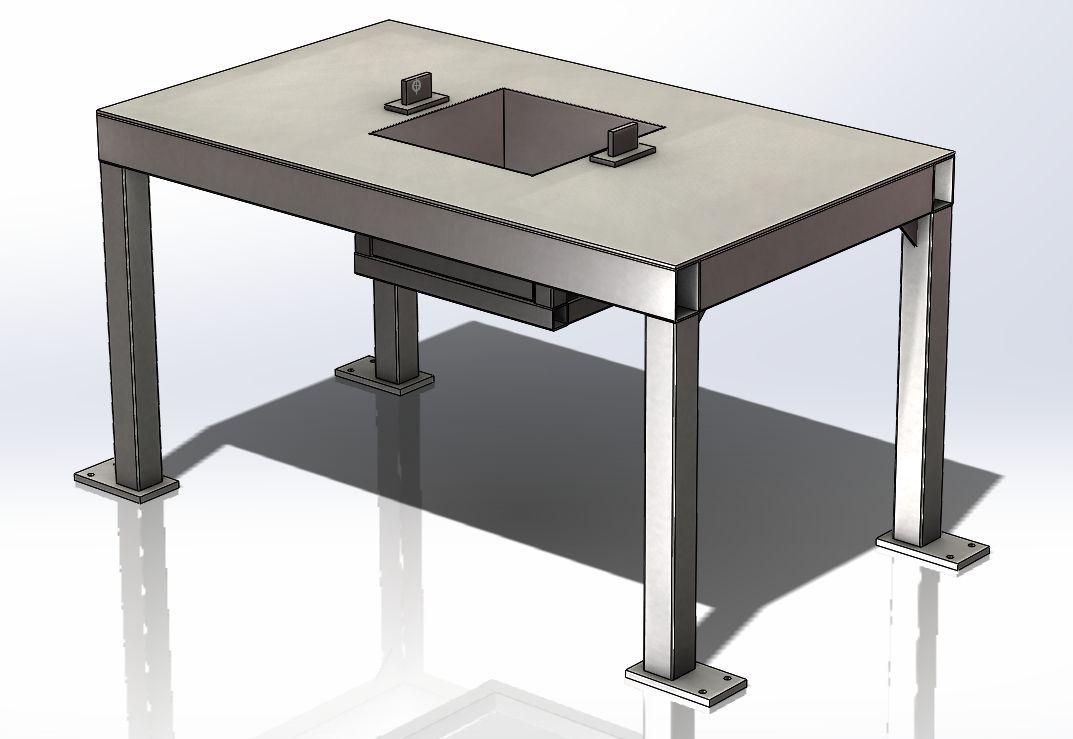
SOLIDWORKS实用技巧之焊件轮廓应用
1.焊件轮廓库官方下载入口 焊件轮廓可以自制,也可以从软件中在线下载获取直接使用,如图1,联网状态按ctrl左键点击下载,解压后获得库文件。 图1 图2 2.库放置的位置和配置 从SOLIDWORKS2014版起,软件焊件轮廓库支持可…...

本地浏览器全局翻译 demo 以火狐firefox为例【免费-简单】
translateDemo 介绍使用说明简单到流泪 本地浏览器全局翻译 demo 以火狐firefox为例 1、安装插件 使用少量的 JavaScript 脚本,自由定义网页显示与运行方式。2、将上述脚本 追加到 插件中即可实现全局翻译;3、免费;参与贡献特技 translateDe…...

使用多线程处理List数据
最近遇到了一个业务场景,需要对List中的数据逐个发起http请求(List中的数据各自独立,对执行顺序无要求),考虑到可以使用多线程加快处理速度。 封装了如下方法: /// <summary>/// 多线程处理数据-无返回值/// </summary&…...

Elasticsearch--Python使用、Django/Flask集成
一、Python使用 from elasticsearch import Elasticsearchobj Elasticsearch() # 创建索引(Index) result obj.indices.create(indexuser, body{"userid":1,username:lqz},ignore400) # print(result) # 删除索引 # result obj.indices.de…...
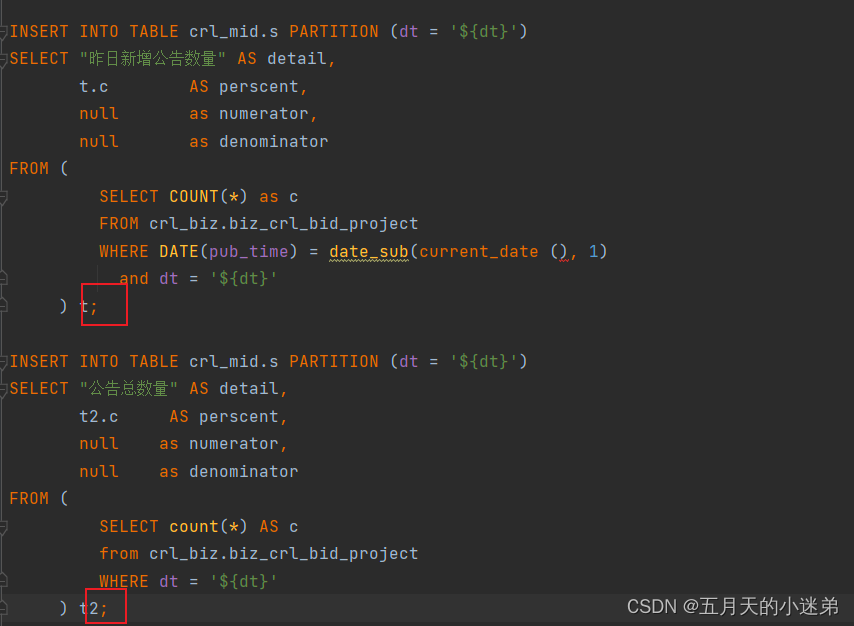
pyspark将数据多次插入表的时候报错
代码 报错信息 py4j.protocol.Py4JJavaError: An error occurred while calling o129.sql. : org.apache.spark.sql.catalyst.parser.ParseException: mismatched input INSERT expecting <EOF>(line 12, pos 0) 原因 插入语句结束后没有加;结尾 把两个&am…...

Qt绘制饼状图
必须在MainWindow.h头文件开头放 #include <QtCharts> //必须这么设置 创建chart: void MainWindow::iniPiewChart() { //饼图初始化QChart *chart new QChart();chart->setTitle(" Piechart演示");chart->setAnimationOptions(QChar…...
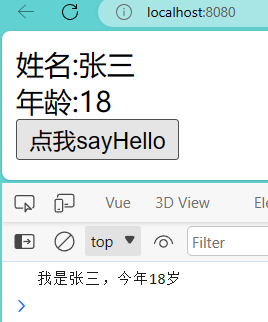
Vue3 setup函数
一、setup函数介绍 setup函数是Vue3中全新的一个配置项,值为一个函数,是所有 Composition API 中“表演的舞台”。 我们在Vue2中用到的所有数据、方法,都需要配置在setup中。 这是我们在Vue2中的写法: 这是我们在Vue3 setup中的…...
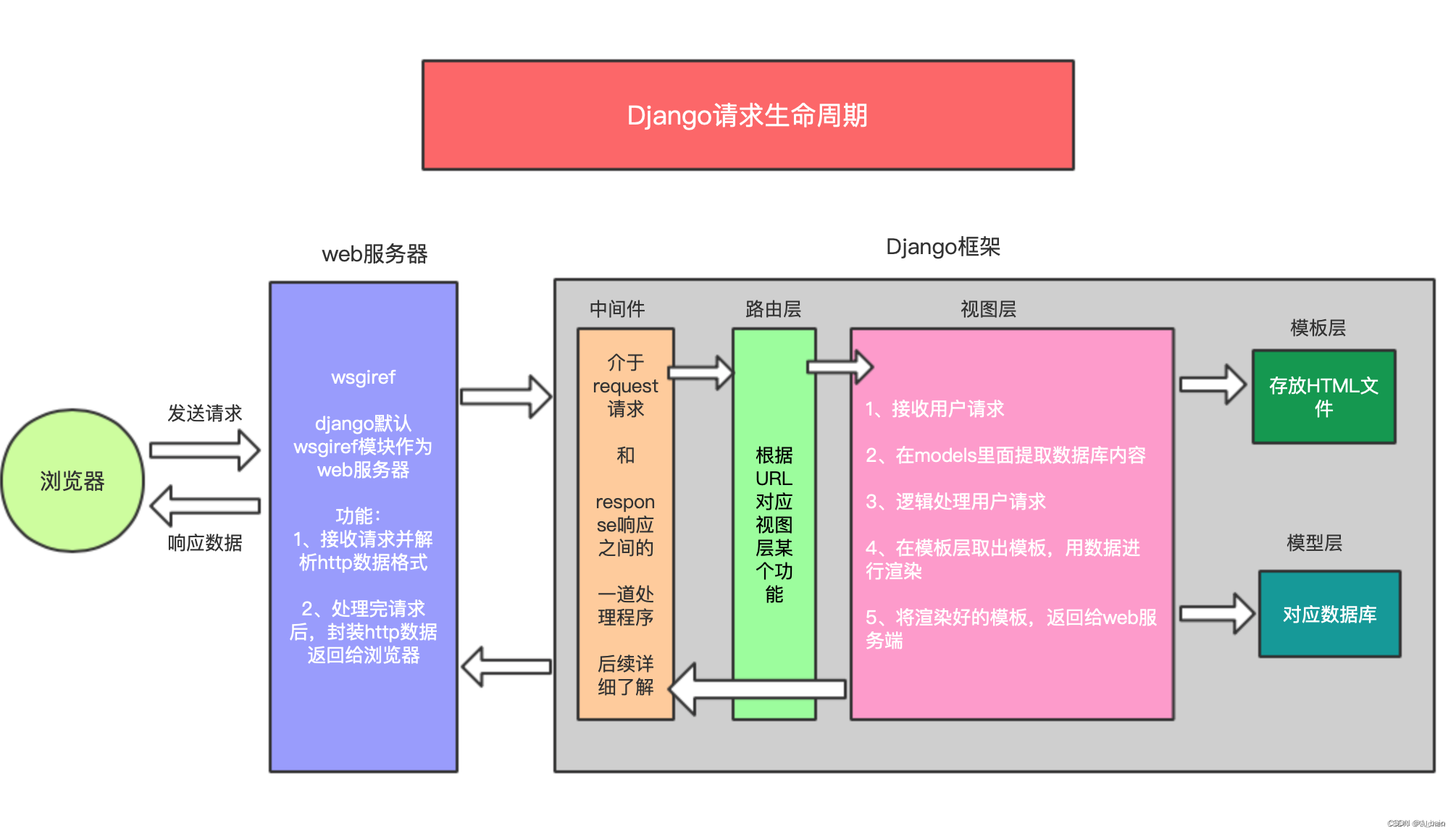
Django(三、数据的增删改查、Django生命周期流程图)
文章目录 一、 基于ORM进行的CURDuser_list:作为主页使用路由文件urls.py配置如下:add.html:用于新增用户的数据页add页面视图函数如下:edit.html:修改数据的页面那么来总结一下上序所操作所用到的内容。 导入已存在的表其方式有两…...

Linux 部署Sentinel控制台
Sentinel 是面向分布式、多语言异构化服务架构的流量治理组件,主要以流量为切入点,从流量路由、流量控制、流量整形、熔断降级、系统自适应过载保护、热点流量防护等多个维度来帮助开发者保障微服务的稳定性。 1.版本选择 SpringCloudAlibaba SpringClo…...

服务器如何下载百度网盘数据
百度网盘作为镜像 国外用户传数据到我们服务器比较慢,但是传输百度网盘速度还是可以的。 这样我们就可以将百度网盘作为一个文件中转站。 但Linux系统下使用百度网盘有些麻烦,虽然百度网盘也有Linux版本,但服务器没开启图形界面,使用的是命令行。这个时候就得感谢开发者Ho…...
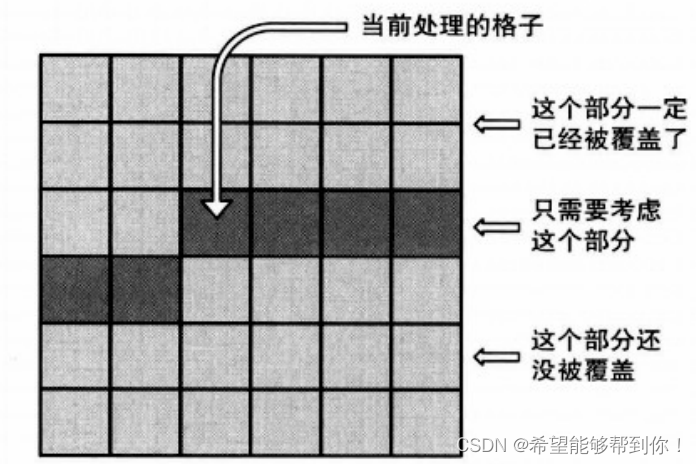
POJ 3254 Corn Fields 状态压缩DP(铺砖问题)
一、题目大意 我们要在N * M的田地里种植玉米,有如下限制条件: 1、对已经种植了玉米的位置,它的四个相邻位置都无法继续种植玉米。 2、题目中有说一些块无论如何,都无法种植玉米。 求所有种植玉米的方案数(不种植也…...
transformers安装避坑
1.4 下载rust编辑器 看到这里你肯定会疑惑了,我们不是要用python的吗? 这个我也不知道,你下了就对了,不然后面的transformers无法安装 因为是windows到官网选择推荐的下载方式https://www.rust-lang.org/tools/install。 执行文…...
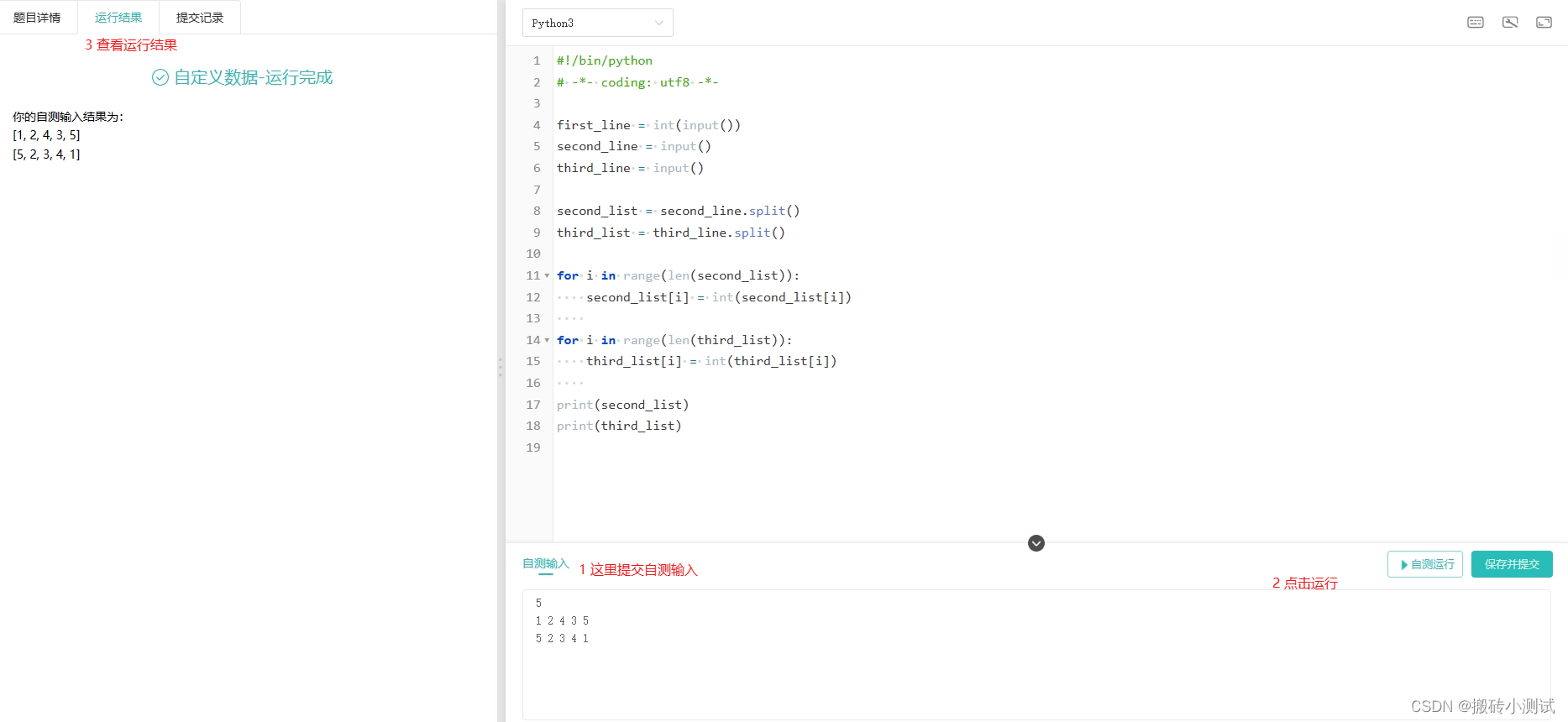
牛客、赛码网OJ调试(全)
现在无论开发还是测试,面试的时候都需要考察代码能力。 从测试的职业发展来看,现在市场上对于纯功能测试的需求很少,招聘方均要求面试者一方面具备测试基础能力,也要求有点代码能力。 对于测试来说,除了测试开发&#…...

【CSS】全局声明引入自定义字体
以下用vue项目为例,其他的也是类似! 在Vue.js中可以使用全局样式表来定义字体。通常,可以在项目中的主样式表中定义全局字体,然后确保该样式表在整个应用程序中被引入。 以下是一般的步骤: 在项目中创建一个全局样式…...

「Flask」路由+视图函数
路由 路由的作用是将 HTTP 请求的 URL 路径映射到相应的函数处理程序。这样我们在开发过程中,就能将不同的 URL 路径与相应的函数处理程序关联起来,从而实现对 Web 应用的灵活控制。 路由可以分为静态路由和动态路由。两者主要是在形式上有一些区别&am…...

信息系统项目管理师 教材目录、考试大纲、考情
文章目录 考情考试大纲第1章 信息化发展第2章 信息技术发展第3章 信息系统治理第4章 信息系统管理第5章 信息系统工程第6章 项目管理概论第7章 项目立项管理第8章 项目整合管理第9章 项目范围管理272第10章 项目进度管理297第11章 项目成本管理334第12章 项目质量管理358第13章…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
