Sequence(矩阵连乘+数论)
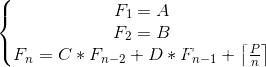
求Fn mod 1e9+7
Input
第一行是一个t代表有t组数据 接下来有t行每行有6个整数A,B,C,D,P,n 1<=t<=10 0<=A,B,C,D<=1e9 1<=p,n<=1e9
Output
输出一个答案Fn对1e9+7取余
Sample Input
2 1 1 1 1 1 5 1 1 1 1 10 4
Sample Output
9 10
思路:
p/n上取整,一直会随着n的变化而变化,所以我们可以分一段一段的计算;
p/n上取整=(p+n-1)/n=(p-1)/n+1;
有个数学小知识:求∑(1,n)⌊k/i⌋∗i-CSDN博客
当我们知道一段区间的下界i,我们可以利用k/(k/i),求出其上界;
当我们知道一段区间的下界时,可以计算出它的上界,快速幂连乘即可。
代码:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<unordered_map>
#include<map>
using namespace std;
typedef long long LL;
typedef unsigned long long ull;
#define per(i,a,b) for(int i=a;i<=b;i++)
#define ber(i,a,b) for(int i=a;i>=b;i--)
const int N = 1e5;
const long long mod = 1e9+7;
const double eps = 1e-2;
typedef struct data
{
LL m[3][3];
}J;
J Q,E;
LL a, b, c, d, p, n;
J now, e,ans;
LL f[3],tmp[3];
void into()
{
Q= { d,c,1,
1,0,0,
0,0,1 };
E = { 1,0,0,
0,1,0,
0,0,1 };
}
J quickfu(J a, J b)
{
J c;
for (int i = 0; i <= 2; i++)
for (int j = 0; j <= 2; j++)
{
c.m[i][j] = 0;
for (int k = 0; k <= 2; k++)
c.m[i][j] = (c.m[i][j] + a.m[i][k] * b.m[k][j] % mod) % mod;
c.m[i][j] = (c.m[i][j] % mod + mod)%mod;
}
return c;
}
J quick(J a, LL b)
{
J ans = e;
while (b)
{
if (b & 1)
ans = quickfu(ans , a);
b >>= 1;
a = quickfu(a, a);
}
return ans;
}
int main()
{
int T;
cin >> T;
while (T--)
{
cin >> a >> b >> c >> d >> p >> n;
into();
now = Q;
e = E;
if (n == 1)
{
cout << a % mod << endl;
continue;
}
if (n == 2)
{
cout << b % mod << endl;
continue;
}
p -= 1;
f[0] = b, f[1] = a;
for (LL i = 3, j = 1; i <= n; i = j + 1)
{
f[2] = p / i + 1;
LL x =p / i;
if (x == 0)
j = n;
else
j = min(n, p / x);
ans = quick(Q, j - i+1);
for (int l = 0; l <= 2; l++)
{
tmp[l] = 0;
for (int w = 0; w <= 2; w++)
tmp[l] = (tmp[l] + ans.m[l][w] * f[w]) % mod;
}
for (int l = 0; l <= 2; l++)
f[l] = tmp[l];
}
cout <<f[0]<< endl;
}
return 0;
}
相关文章:
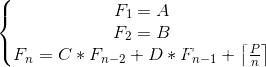
Sequence(矩阵连乘+数论)
求Fn mod 1e97 Input 第一行是一个t代表有t组数据 接下来有t行每行有6个整数A,B,C,D,P,n 1<t<10 0<A,B,C,D<1e9 1<p,n<1e9 Output 输出一个答案Fn对1e97取余 Sample Input 2 1 1 1 1 1 5 1 1 1 1 10 4 Sample Output 9 10 思路: p/n上…...

集合工具类的常用方法--小总和
前言 集合工具类是Java中的一个重要工具类,在Java常用的集合框架中起到了重要的作用。集合工具类提供了一系列的方法,可以方便地处理Java中的集合对象,提高了开发的效率。 Collections类 Collections.sort(List<T> list) 对List集合进…...
)
一文了解游戏行业(数据分析)
一.概况 1.基本术语 游戏行业基础术语——持续更新ing... 2.产业链 包括游戏开发,发行和销售等环节 ①游戏开发 上游环节是游戏产业链的核心环节,包括游戏策划,美术设计,程序开发等,是决定游戏质量与内容的关键因…...

Flutter之Json序列化
前言 使用 json_annotation 框架实现json字符串序列化和反序列化 框架官方地址:json_serializable 一、引入依赖:在pubspec.yaml中添加 dependencies:json_annotation: ^4.8.1dev_dependencies:build_runner: ^2.3.3json_serializable: ^6.6.0 二、…...

Java基础——局部变量和常量
变量:内存中的一个存储区域(该区域的数据可以在同一类型范围内不断变化)。 常量:一旦声明就不可变,通常用 final 修饰的变量称为常量。 声明格式: [final] 变量类型 变量名;说明: final修饰…...
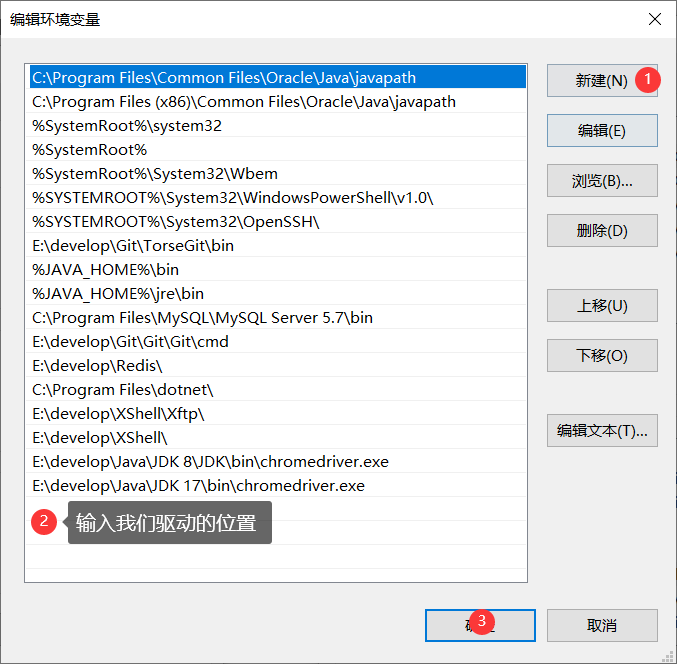
番外 1 : Java 环境下的 selenium 搭建
Java 环境下的 selenium 搭建 一 . 下载谷歌浏览器二 . 下载谷歌浏览器驱动2.1 查看谷歌浏览器版本2.2 下载对应版本的谷歌驱动2.3 解压下载好的驱动压缩包 , 将下载好的 chromedriver.exe 放到java 系统环境变量下 三 . 下载 Edge 浏览器的驱动3.1 查看 Edge 浏览器的版本3.2 …...
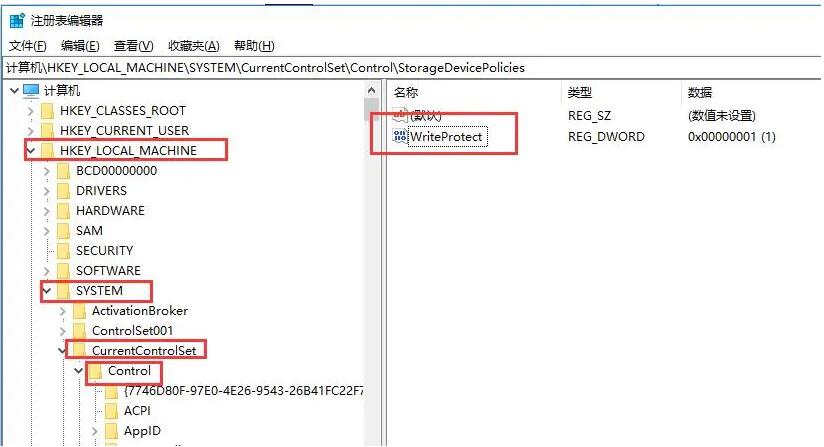
游戏缺失d3dx9_39.dll的5个修复方法,深度解析d3dx9_39.dll文件的作用
在当今的数字化时代,电子游戏已经成为了人们休闲娱乐的重要方式之一。然而,对于许多玩家来说,他们在享受游戏带来的乐趣的同时,也可能会遇到各种各样的问题,其中最常见的就是游戏无法正常运行。而这些问题中࿰…...

RHCSA --- Linux用户/组权限
用户管理 useradd 创建用户 -u(UID) 指定UID -g(GID) 指定基本组 -G(GID1,GID2,...) 指定附加组 -c “注释信息” 指定用户注释信息(昵称) -d /path…...
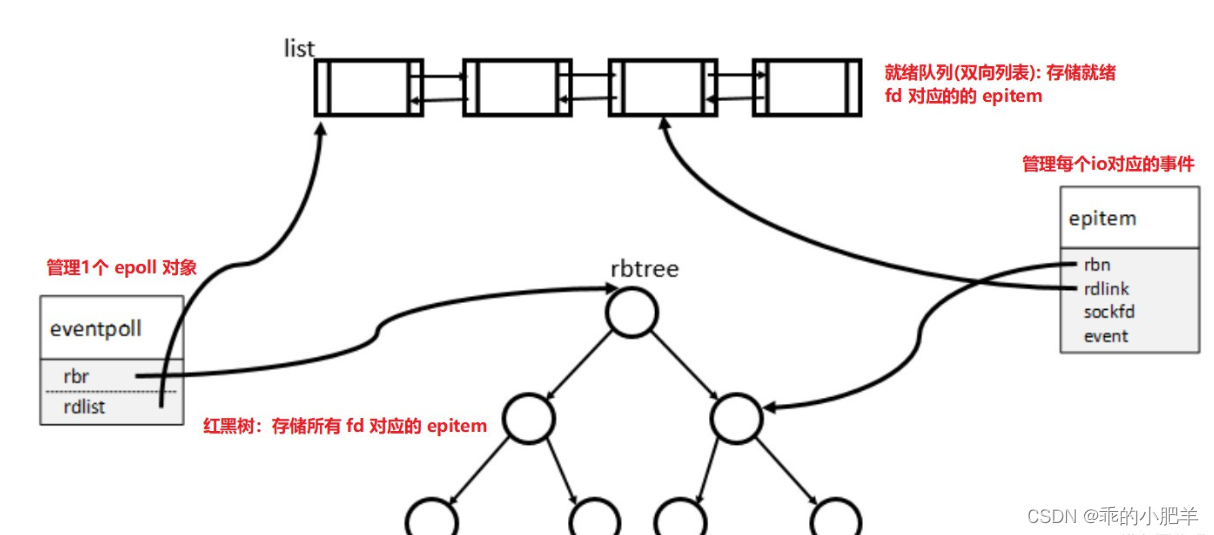
怎么做到高性能网络IO?
为什么要做高性能网络IO。主要是解决c10,c10M问题 最开始的时候我们走的内核协议栈,走内核协议栈其实性能比较低,因为我们之前介绍的时候需要拷贝两次 但是我们采用用户态协议栈可以少拷贝一次,可以大大提高效率, 步骤…...

设计模式-创建型
文章目录 设计模式-创建型工厂模式简单工厂工厂方法抽象工厂 建造者模式单例模式原型模式 设计模式-创建型 本章主要介绍有关对象创建的几种设计模式。 工厂模式 工厂模式:封装了对象的创建,使得获得对象更加符合实际逻辑 简单工厂 将所有对象的生产…...
Word通过Adobe打印PDF时总是报错,打开记事本
Word文档打印,选择Adobe作为打印机,打印过程中总是报错,不断打开记事本,提示打印出错,错误信息如下: %%[ ProductName: Distiller ]%% %%[Page: 1]%% %%[Page: 2]%% %%[ Error: invalidfont; OffendingCom…...
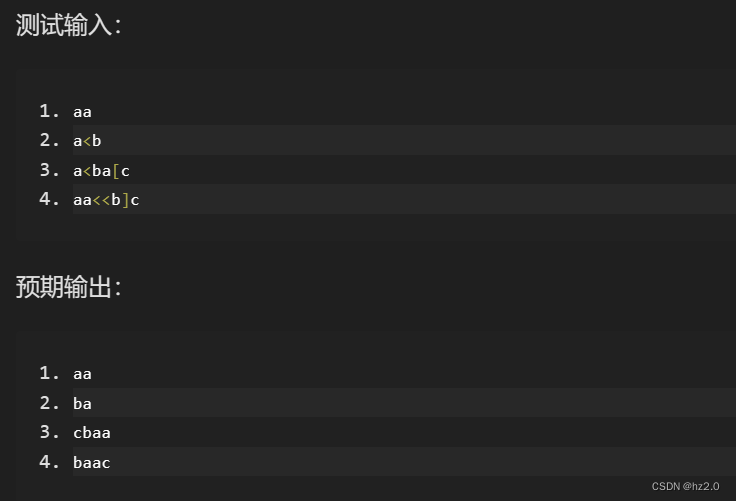
第2关:还原键盘输入(list)
题目: 知识点: 列表list相较于数组: 优势:可在任意指定位置插入或者删除元素而不影响列表其他地方 。 劣势:无法直接进行下标索引,需要迭代器it逐个遍历。 代码: #include <iostream>…...
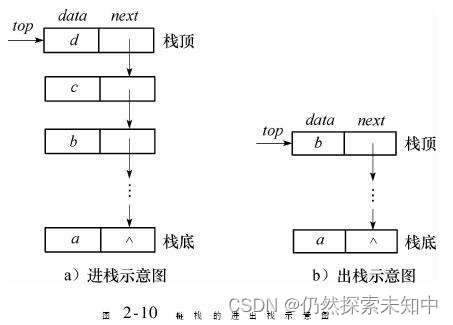
数据结构 | 栈的实现
数据结构 | 栈的实现 文章目录 数据结构 | 栈的实现栈的概念及结构栈的实现 Stack.h初始化栈入栈出栈获取栈顶元素获取栈中有效元素个数检测栈是否为空销毁栈 Stack.c 栈的概念及结构 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。…...
python异常、模块与包
1.异常 异常:当检测到一个错误时,Python解释器就无法继续执行了,反而出现了一些错误的提示,这就是所谓的“异常”,也就是我们常说的BUG。 1.1捕获异常 基本语法: try:可能发生错误代码 except:如果出现…...

虚拟内存和物理内存
虚拟内存的概念 虚拟内存是计算机系统内存管理的一种技术,它使得应用程序认为它拥有连续可用的内存(一个连续完整的地址空间),而实际上,它通常是被分隔成多个物理内存碎片,还有部分暂时存储在外部磁盘存储…...

FCA例题
Part.1:判断题 第1题 智能运维-负载管理中,实时负载通过使用图表直观的展示当前系统的最多最近半小时内存利用率和CPU利用率(正确) 第2题 服务器安装插件支持热部署,安装、删除、更新、禁用、启用不需要重启(正确) 第3题 次级管理员可新建…...

mysql使用GROUP BY归组后把所有记录id汇总到一个字段中
可以使用MySQL的GROUP_CONCAT函数来实现将归组后的记录的ID汇总到一个字段中。假设有一个名为table1的表,其中包含id和name两个字段,可以使用以下查询: SELECT name, GROUP_CONCAT(id) AS ids FROM table1 GROUP BY name;这将返回一个结果集…...

Vue3 使用Element Plus表格单选带checkbox
官方地址:添加链接描述 官方给出的多选带checkbox,单选直接选中当前行高亮,有时候不想要单行高亮,想要带checkbox的单选,需要对多选进行改造 官方给的多选例子: <template><el-tableref"mult…...

IOC - 自定义IOC容器
1、定义接口与实现类 // Service接口 public interface Service {void execute(); } // Service的实现类 public class MyService implements Service {Overridepublic void execute() {System.out.println("MyService 执行了.");} }2、自定义ioc容器以绑定接口与实…...
力扣第647题 回文子串 c++ 动态规划 双指针 附Java代码 注释解释版
题目 647. 回文子串 中等 相关标签 字符串 动态规划 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
