【DP】背包问题全解
一.简介
DP(动态规划)背包问题是一个经典的组合优化问题,通常用来解决资源分配的问题,如货物装载、投资组合优化等。问题的核心思想是在有限的资源约束下,选择一组物品以最大化某种价值指标,通常是总价值或总利润。
二.闫氏DP分析法

三.01背包
(1)概念
每个物品只有一个,要么选,要么不选
(2)状态转移方程
f[i][j] = max(f[i-1][j] , f[i-1][j-v]+w)
(3)经典例题
P1048 [NOIP2005 普及组] 采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
(4)代码
#include<bits/stdc++.h>
#define N 1010
using namespace std;
int f[N][N];
int w[N],c[N];
int bag,n;
int main(){scanf("%d%d",&bag,&n);for(int i=1;i<=n;i++) scanf("%d%d",&w[i],&c[i]);for(int i=1;i<=n;i++){for(int j=0;j<=bag;j++){f[i][j]=f[i-1][j];if(j>=w[i]){f[i][j]=max(f[i][j],f[i-1][j-w[i]]+c[i]);}}}printf("%d",f[n][bag]);return 0;
}(5)滚动数组优化
#include<bits/stdc++.h>
#define N 1010
using namespace std;
int f[N];
int n,m;
int main()
{scanf("%d%d", &m, &n);for(int i = 1; i <= n; i ++ ){int w,c;scanf("%d%d", &w, &c);for(int j = m; j >=w ; j -- ){ f[j] = max(f[j], f[j-w] + c);}}printf("%d", f[m]);return 0;
}四.完全背包
(1)概念
每个物品有无限个
(2)例题
1023. 买书 - AcWing题库
(3)闫氏DP分析法

(4)状态转移方程推导
f[i][j] = f[i - 1][j] + f[i - 1][j - v * 1] + f[i - 1][j - v * 2] + ...... + f[i -1][j - v * k];
f[i][j - v] = f[i - 1][j - v * 1] + f[i - 1][j - v * 2] + ...... + f[i - 1][j - v * k];
所以推出:f[i][j] = f[i - 1][j] + f[i][j - v];
再使用滚动数组简化,就得出结论,其实就是01背包,内循环从大到小变成了从小到大!
(5)参考代码
#include<bits/stdc++.h>
#define N 1010
using namespace std;
int f[N];
int n;
int a[5] = {0, 10, 20, 50, 100};int main(){scanf("%d", &n);f[0] = 1; for(int i = 1; i <= 4; i ++ ){for(int j = a[i]; j <= n; j ++ ){f[j] += f[j - a[i]];}} printf("%d", f[n]);return 0;
}五.多重背包
(1)概念
物品有一定的数量
(2)实现方式
1.朴素版(易) 2.二进制优化版(中) 3.单调队列优化版(难)
(3)经典例题
1019. 庆功会 - AcWing题库
(3)朴素版
#include<bits/stdc++.h>
#define N 6010
using namespace std;
int f[N];
int n, m;
int main(){scanf("%d%d", &n, &m); //n个物品,m容量 for(int i = 1;i <= n; i ++ ){int v, w, s; //容量,价值,数量 scanf("%d%d%d", &v, &w, &s);for(int j = m; j >= v; j -- ){ //枚举容量 for(int k = 1;k <= s && k * v <= j; k ++ ){ //再枚举数量 f[j] = max(f[j], f[j - k * v] + w * k);}}}printf("%d", f[m]);return 0;
}(4)二进制优化版
#include<bits/stdc++.h>
#define N 6010
using namespace std;
int f[N];
int n,m;
int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= n ; i ++ ){int v, w, s;scanf("%d%d%d", &v, &w, &s);for(int k = 1; k <= s; k *= 2) //二进制分解{for(int j = m; j >= k * v; j --)f[j] = max(f[j], f[j - k * v] + k * w);s -= k;}if(s) //余下的{for(int j = m; j >= s * v; j --)f[j] = max(f[j], f[j - s * v] + s * w);}}printf("%d", f[m]);return 0;
}六.分组背包
(1)概念
每组物品有若干个,同一组内的物品最多只能选一个。
和多重背包十分相似,也简单。难得写了,copy一下,哈哈。

七.混合背包
(1)概念
就是把完全背包,多重背包,01背包混合起来,分类讨论即可,代码很好看懂。
(2)例题
7. 混合背包问题 - AcWing题库
(3)参考代码
#include<bits/stdc++.h>
#define N 1010
using namespace std;
int f[N];
int n,m;
int main()
{scanf("%d%d", &n, &m);int v, w, s;for(int i = 1; i <= n; i ++ ){scanf("%d%d%d", &v, &w, &s);if(s == 0){for(int j = v; j <= m; j ++ )f[j] = max(f[j], f[j - v]);}else{if(s == -1) s = 1;for(int k = 1; k <= s; k *= 2){for(int j = m; j >= k * v; j --)f[j] = max(f[j], f[j - k * v] + k * w);s -= k;}if(s){for(int j = m; j >= s * v; j --)f[j] = max(f[j], f[j - s * v] + s * w);}}}printf("%d", f[m]);return 0;
}八.有依赖的背包
(1)例题
10. 有依赖的背包问题 - AcWing题库
(2)参考代码
#include<iostream>
#include<vector>
using namespace std;
int f[110][110];//f[x][v]表达选择以x为子树的物品,在容量不超过v时所获得的最大价值
vector<int> g[110];
int v[110],w[110];
int n,m,root;int dfs(int x)
{for(int i=v[x];i<=m;i++) f[x][i]=w[x];//点x必须选,所以初始化f[x][v[x] ~ m]= w[x]for(int i=0;i<g[x].size();i++){int y=g[x][i];dfs(y);for(int j=m;j>=v[x];j--)//j的范围为v[x]~m, 小于v[x]无法选择以x为子树的物品{for(int k=0;k<=j-v[x];k++)//分给子树y的空间不能大于j-v[x],不然都无法选根物品x{f[x][j]=max(f[x][j],f[x][j-k]+f[y][k]);}}}
}int main()
{cin>>n>>m;for(int i=1;i<=n;i++){int fa;cin>>v[i]>>w[i]>>fa;if(fa==-1)root=i;elseg[fa].push_back(i);}dfs(root);cout<<f[root][m];return 0;
}
九.二维费用背包
(1)简介
其实就是多了一维,和一维费用没啥区别
二维背包可以结合上述所有背包!
(2)例题
8. 二维费用的背包问题 - AcWing题库
(3)参考代码
#include<bits/stdc++.h>
#define maxn 1005
using namespace std;
int f[maxn][maxn];
int n,V,M;
int main(){scanf("%d%d%d",&n,&V,&M);for(int i=1;i<=n;i++){int v,m,w;scanf("%d%d%d",&v,&m,&w);//就是这里多了一维,多了一个循环,很好理解for(int j=V;j>=v;j--){for(int k=M;k>=m;k--){f[j][k]=max(f[j][k],f[j-v][k-m]+w);}}}printf("%d",f[V][M]);return 0;
}十.总结
1.只有完全背包是正序遍历的,其他背包都是倒序遍历!
2.背包模型显而易见都是题目中给有一定的约束,如:有个多大容积的背包,有多少钱,等等。然后就是有几种方案,又给出相其对应的代价和贡献,最后求MAX or Count。
3.DP核心就在于熟练掌握闫氏DP分析法和题刷多了,积累了足够多的状态转移方程。
4.其实背包问题并不难,待到题刷够了,一切就迎刃而解了!加油!!!
相关文章:

【DP】背包问题全解
一.简介 DP(动态规划)背包问题是一个经典的组合优化问题,通常用来解决资源分配的问题,如货物装载、投资组合优化等。问题的核心思想是在有限的资源约束下,选择一组物品以最大化某种价值指标,通常是总价值或…...
)
04 jenkins中使用各种变量(Powershell、cmd)
批处理中使用jenkins内部和变量插件定义的环境变量:%WORKSPACE%Powershell插件中使用jenkins内部环境变量:${ENV:WORKSPRACE}Powershell函数内部使用函数入参:$($dllname)Powershell中定义变量:$DllNamePowershell中使用powershel…...
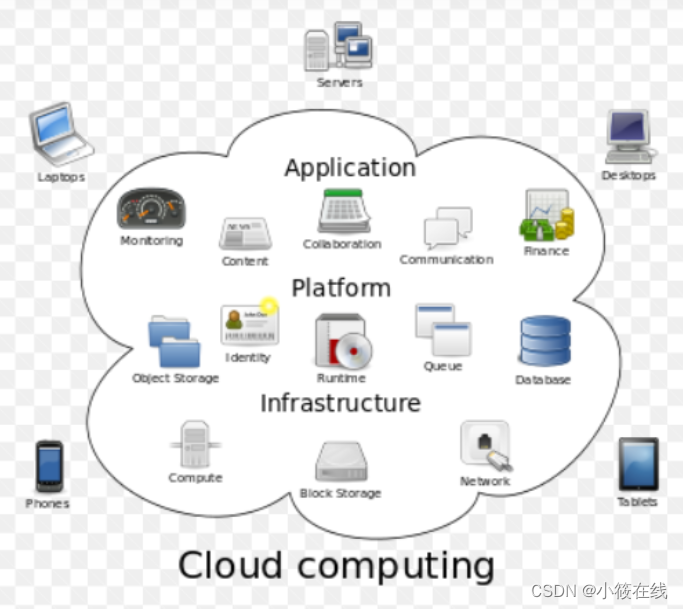
2023年云计算的发展趋势
随着互联网和信息技术的快速发展,云计算已经成为了企业和个人的重要工具,而在未来,云计算仍然会持续发展,并且发展趋势会更加迅猛。在本文中,我们将讨论2023年云计算的发展趋势。 一、混合云将成为主流 混合云是指将公…...

工作十年+的测试应该具备什么能力?
大概是2014年的时候,我开始接触面试工作,就是从应聘者转为面试官,记得印象深刻的是面试了一位做了8年的测试。对方气场很足,嗯,毕竟那时的我还只是一个3、4年经验的小测试,相反,印象深刻的并不是…...

区块链链游合约系统开发项目模式技术方案
随着区块链技术的发展,链游合约系统开发逐渐成为了一个备受关注的项目。本文将探讨区块链链游合约系统开发项目的技术方案,包括项目背景、开发目标、技术架构、系统流程、安全措施等方面的内容。 一、项目背景 链游是一种基于区块链技术的游戏…...
业务出海之服务器探秘
这几年随着国内互联网市场的逐渐饱和,越来越多的公司加入到出海的行列,很多领域都取得了很不错的成就。虽然出海可以获得更加广阔的市场,但也需要面对很多之前在国内可能没有重视的一些问题。集中在海外服务器的选择维度上就有很大的变化。例…...
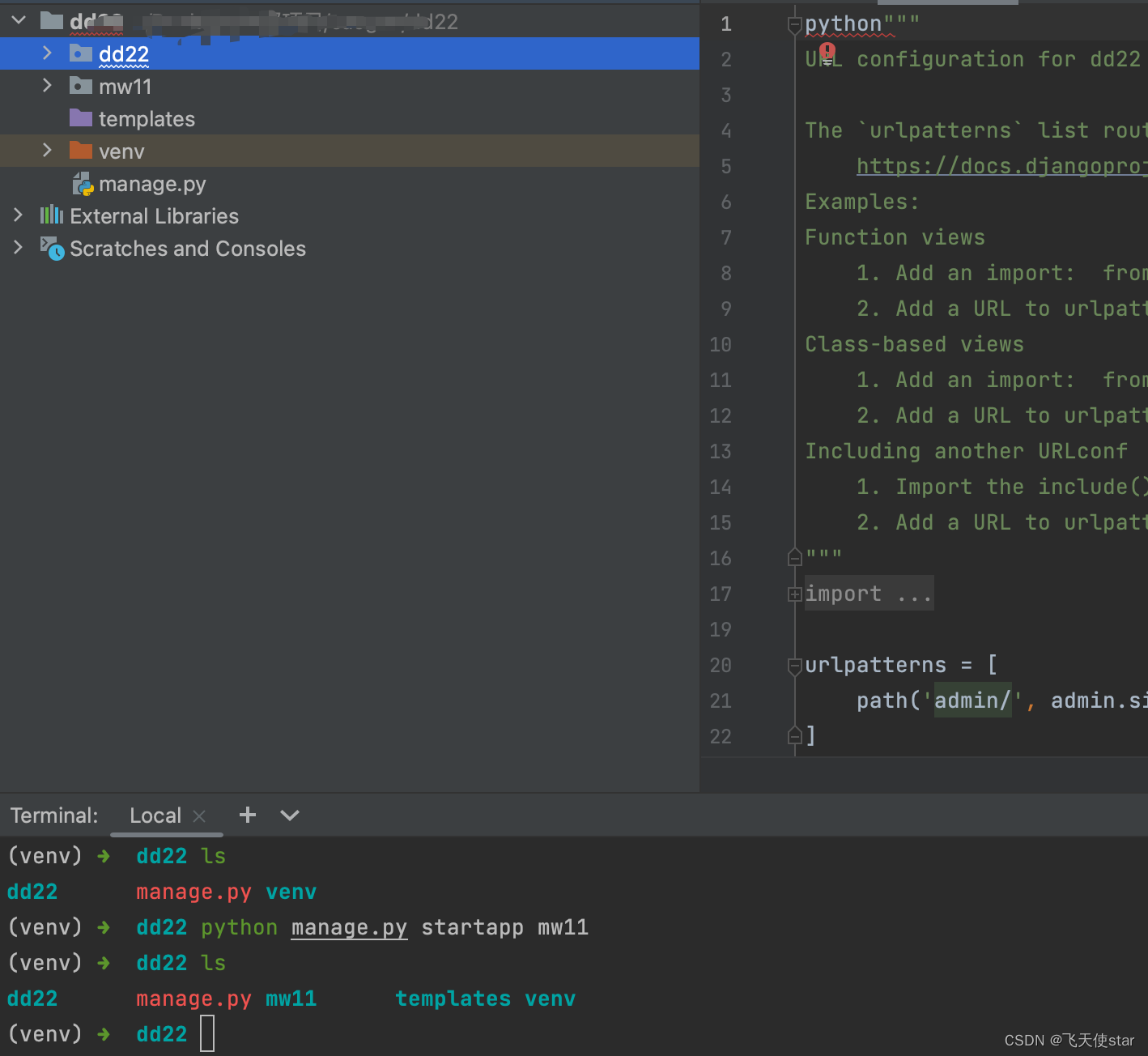
飞天使-django创建一个初始项目过程
创建django项目 运行项目 运行命令 pyhont manage.py runserver 然后访问 http://127.0.0.1:8000/, 则可以打开本地新建的项目 虚拟环境的部署-mac 在一台计算机上可以通过虚拟环境实现多个版本Django的开发环境 安装虚拟环境工具:如果你的系统中没有安…...
)
【工具插件类教学】全局积雪系统和雪痕迹显示(移动痕迹)
目录 一、演示场景对比效果 二、导入工具插件 三、使用流程 1.添加脚本组件GlobalSnow...
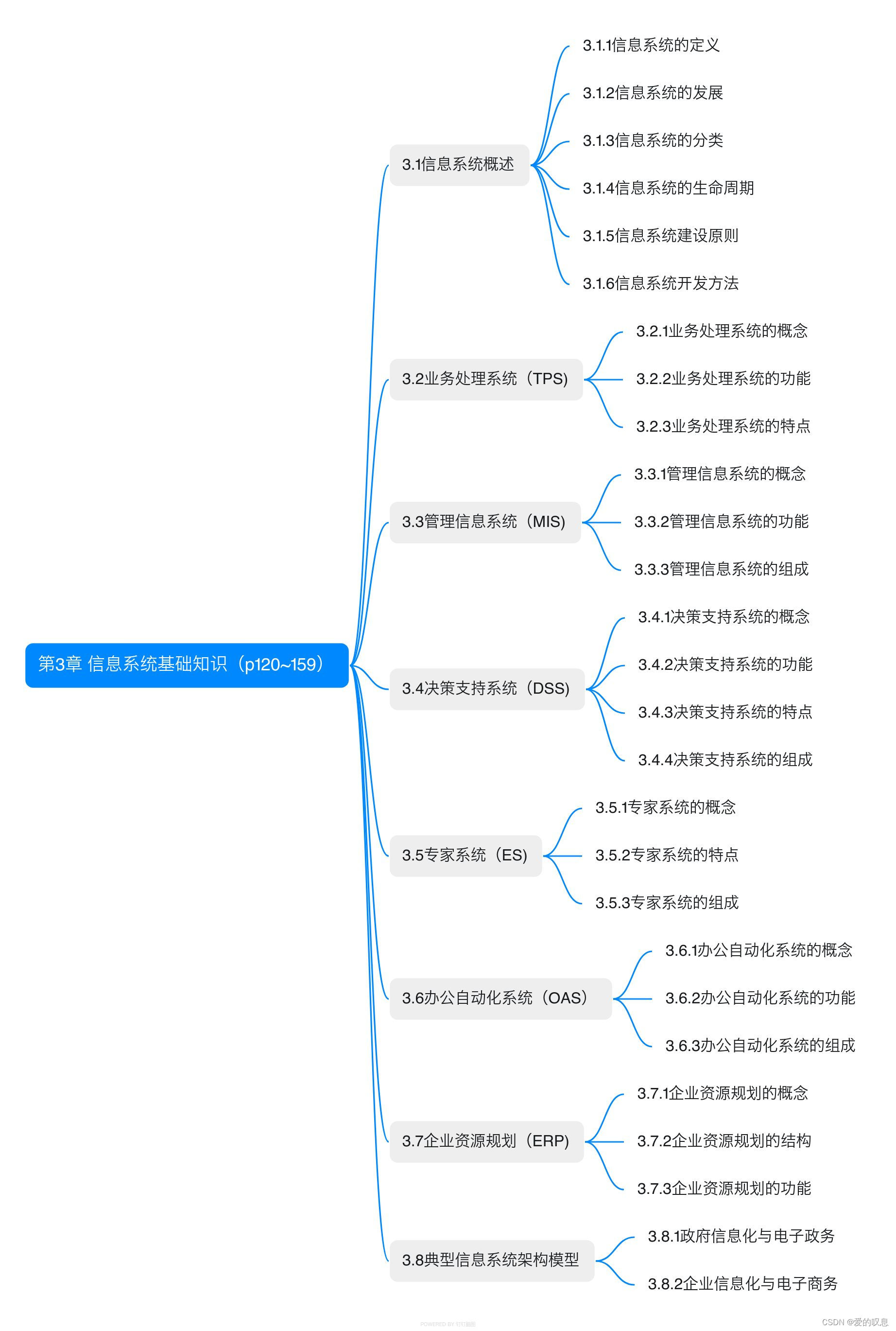
软考-高级-系统架构设计师教程(清华第2版)【第3章 信息系统基础知识(p120~159)-思维导图】
软考-高级-系统架构设计师教程(清华第2版)【第3章 信息系统基础知识(p120~159)-思维导图】 课本里章节里所有蓝色字体的思维导图...

STM32基础--NVIC中断控制器
一、NVIC是什么? NVIC是一种中断控制器。当一个中断正在处理时,另一个更高优先级的中断可以打断当前中断的执行,并立即得到处理。这种机制使得处理器在高速运行的同时,能够及时响应不同优先级的中断请求。 二、有哪些优先级&…...

使用matlab实现图像信号的色彩空间转换
利用matlab对图像信号进行读取,并对RGB空间进行转换,如转换到HSI空间等。 下面的这个代码是在使用了rgb2hsi()方法失败后,进行修改的。 rgb2hsi(img)这个方法可以将RGB图像转换为HIS图像;但是爆出了 Untitled5(line 5)hsi rgb2h…...

Vatee万腾科技决策力的引领创新:Vatee数字化视野的崭新天地
在数字时代的激烈竞争中,Vatee万腾以其科技决策力的引领,开创了数字化视野的崭新天地。这并不仅仅是一场技术的飞跃,更是一次对未来的深刻洞察和引领创新的勇敢实践。 Vatee万腾的科技决策力不仅仅停留在数据分析和算法的运用,更是…...
Go语言安装教程
【Go系列-1】-Go安装教程 环境提前准备 安装的时候可以选择自己的目录进行环境管理 E:\Z_Enviroment\Go创建文件夹: E:\Z_Enviroment\Go E:\Z_Enviroment\GoWorks E:\Z_Enviroment\GoWorks\bin E:\Z_Enviroment\GoWorks\pkg E:\Z_Enviroment\GoWorks\src环境变量…...
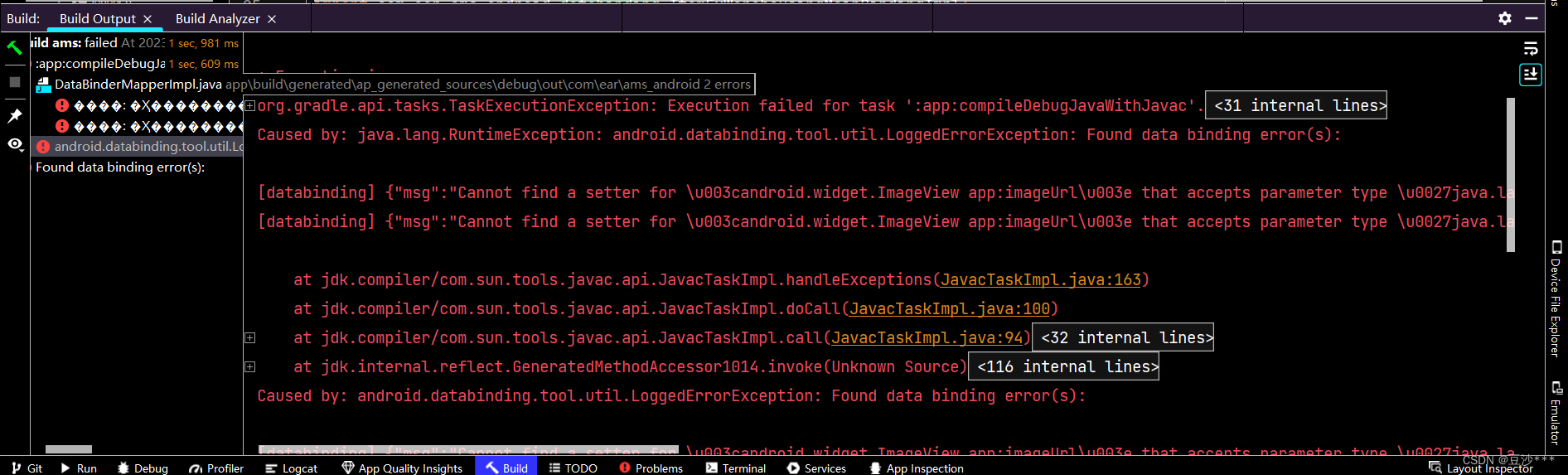
MVVM框架:图片加载有问题
一、前言:在我使用ImageView加载图片的时候添加如下代码发现报错 app:imageUrl"{viewModel.observableField.assetImg}"报错如下错误 二、原因:是啥我不太清楚好像是没有imageView的适配器,后来我看了一下确实没有 public class I…...
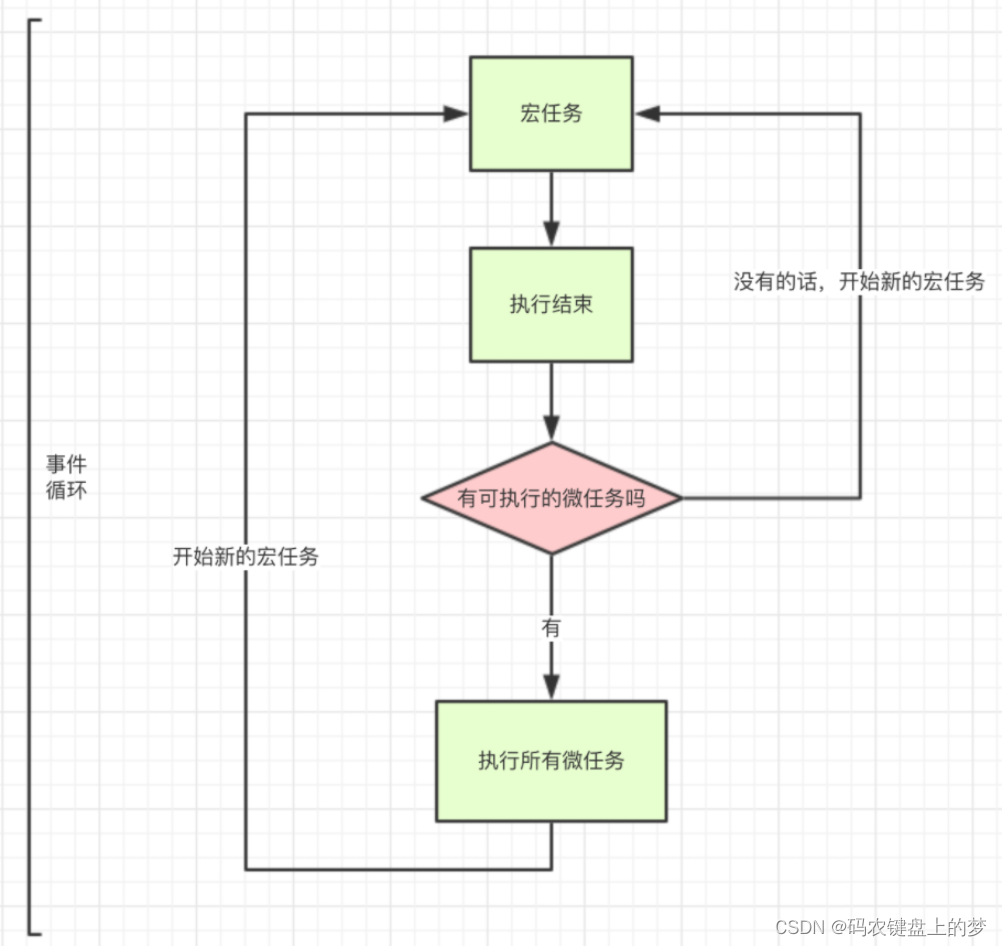
一篇文章搞明白js运行机制——事件循环
1、解释 JavaScript 的执行机制。 JavaScript 的执行机制基于事件循环。事件循环包括一个任务队列(Task Queue)和一个微任务队列(Microtask Queue)。当一个函数被调用时,它被添加到微任务队列中。事件循环每次迭代都会…...

Leetcode 第 371 场周赛题解
Leetcode 第 371 场周赛题解 Leetcode 第 371 场周赛题解题目1:100120. 找出强数对的最大异或值 I思路代码复杂度分析 题目2:100128. 高访问员工思路代码复杂度分析 题目3:100117. 最大化数组末位元素的最少操作次数思路代码复杂度分析 题目4…...

keras转onnx,TensorFlow转tf.keras.models.load_model,onnx精度转换
参考: https://blog.csdn.net/Deaohst/article/details/126864267 转onnx 别直接转onnx。 先转PB: import tensorflow as tfmodel_path ./models/model.h5 # 模型文件 model tf.keras.models.load_model(model_path) model.sa…...

高可用架构设计
1. 引言 软件系统有三个追求:高性能、高并发、高可用,俗称三高。三者既有区别也有联系,门门道道很多,本篇讨论高可用 高可用技术的重要性在于保证系统的连续可用性,提高系统的稳定性和可靠性。它可以应对高并发和大规…...
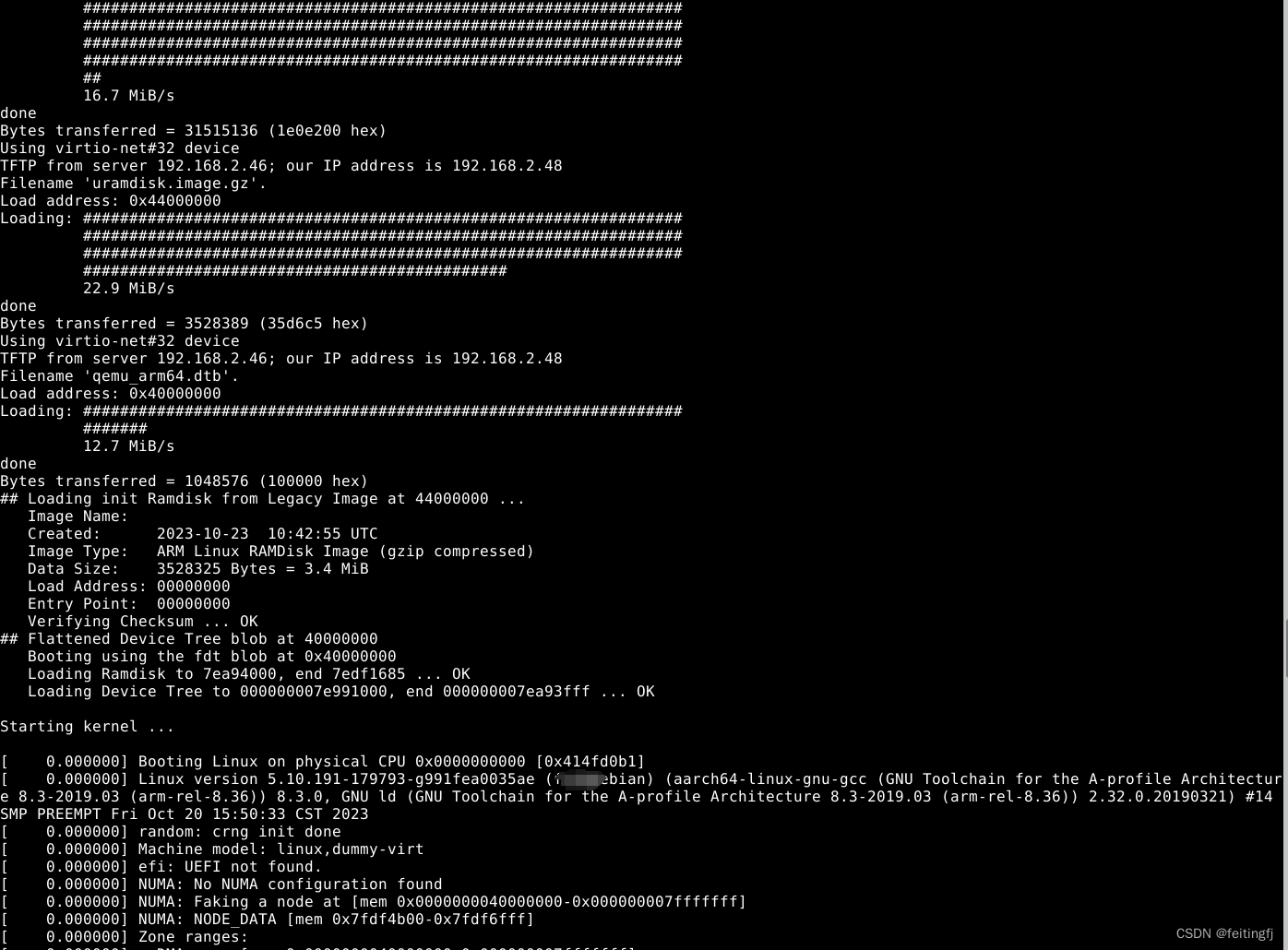
qemu 之 uboot、linux 启动
目录 编译uboot、kernel 编译启动从 uboot 中引导启动 linux注参考 本文主要说明 arm64 在 qemu 上的相关启动。 编译 使用的是 qemu-8.1.1 版本,编译命令如下: ../configure --cc/usr/local/bin/gcc --prefix/home/XXX/qemu_out --enable-virtfs --enable-slir…...
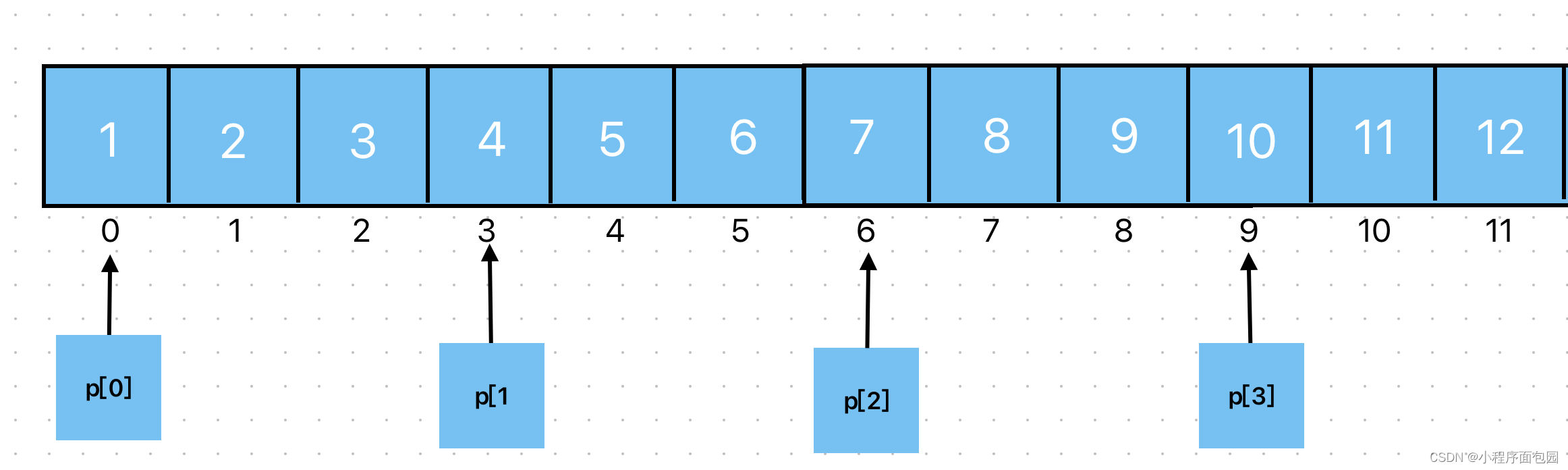
C语言--每日五道选择题--Day8
第一题 1、下列程序的输出是( ) #include<stdio.h> int main() {int a[12] {1,2,3,4,5,6,7,8,9,10,11,12};int *p[4];int i;for(i0;i<4;i){p[i]&a[i*3];}printf("%d\n",p[3][2]);return 0; } A: 上述程序有错误 B: 6…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
