图像二值化阈值调整——Triangle算法,Maxentropy方法
一. Triangle方法
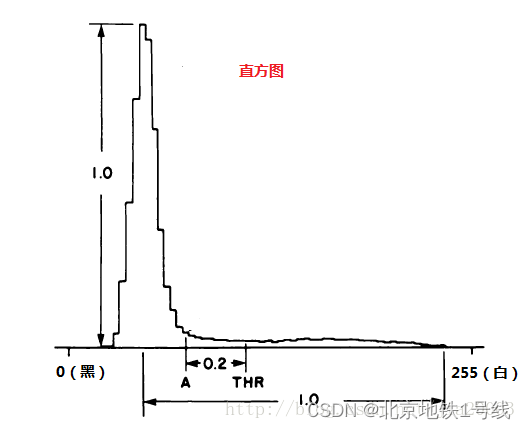
算法描述:三角法求分割阈值最早见于Zack的论文《Automatic measurement of sister chromatid exchange frequency》主要是用于染色体的研究,该方法是使用直方图数据,基于纯几何方法来寻找最佳阈值,它的成立条件是假设直方图最大波峰在靠近最亮的一侧,然后通过三角形求得最大直线距离,根据最大直线距离对应的直方图灰度等级即为分割阈值,图示如下:

三角几何化的过程。首先找到直方图中灰度值最高的一点并判别亮暗,然后找到最左边点,两点连接一条直线,求直方图上离直线最远的点,设置该点的灰度值为阈值。
有时候最大波峰对应位置不在直方图最亮一侧,而在暗的一侧,这样就需要翻转直方图,翻转之后求得值,用255减去即得到为阈值T。扩展情况的直方图表示如下:
算法特点:适用于单峰。这点和OTSU算法有很大区别,OTSU适用于双峰。
cv2中有三角分割的算法,直接使用即可。
import cv2
import matplotlib.pylab as pltdef main():img = cv2.imread('6.jpg', 0)ret, thresh1 = cv2.threshold(img, 0, 255, cv2.THRESH_TRIANGLE)print(ret) # 结果是151.0titles = ['Original Image', 'After Binarization']images = [img, thresh1]for i in range(2):plt.subplot(1, 2, i + 1)plt.imshow(images[i], 'gray')plt.title(titles[i])plt.xticks([])plt.yticks([])plt.show()main()
二. Maxentropy方法
最大熵阈值分割法和OTSU算法类似,假设将图像分为背景和前景两个部分。熵代表信息量,图像信息量越大,熵就越大,最大熵算法就是找出一个最佳阈值使得背景与前景两个部分熵之和最大。
给定一个大小为M*N的图像,直方图中所有矩形框所代表的数值之和,即为图像中的像素数量,设像素值i的像素在图中有个,即:
相对应的归一化直方图表示为:
其中0<=i<K。通常被解释为一个随机过程的概率分布或概率密度函数,表示的是图像中像素灰度值为i所出现的概率。i的累积概率值为1,即概率分布p必须满足以下关系:
与累积概率所对应的累积直方图H是一个离散的分布函数P()(通常也称为累积分布函数或cdf),P(i)表示像素值小于等于i的概率:
在图像处理中,灰度图的熵定义如下:
因为,所以
。
利用图像熵为准则进行图像分割有一定历史了,学者们提出了许多以图像熵为基础进行图像分割的方法。以下介绍一种由Kapuret al提出来,现在仍然使用较广的一种图像熵分割方法。
给定一个特定的阈值q(0<=q<K-1),对于该阈值所分割的两个图像区域C0,C1,这两部分的熵可写为:
其中:,
,
。
图像总熵为:。现在就是要遍历q(0<=q<K-1),使得Hq最大。
为了计算方便,对H(0)和H(1)的表达式进行优化:
得到
同理
其中,
。
import cv2
import matplotlib.pylab as plt
import numpy as np
import mathdef calcGrayHist(image):rows, cols = image.shape[:2]grayHist = np.zeros([256], np.uint64)for row in range(rows):for col in range(cols):grayHist[image[row][col]] += 1return grayHistdef thresh_entropy(image):rows, cols = image.shape# 求灰度直方图grayHist = calcGrayHist(image)# 归一化灰度直方图,即概率直方图normGrayHist = grayHist / float(rows*cols) # 就是上面讲的p(i)# 1.计算累加直方图zeroCumuMoment = np.zeros([256], np.float32) # 就是上面讲的P(i)for i in range(256):if i == 0:zeroCumuMoment[i] = normGrayHist[i]else:zeroCumuMoment[i] = zeroCumuMoment[i-1] + normGrayHist[i]# 2.计算各个灰度级的熵entropy = np.zeros([256], np.float32) # 就是上面讲的S_0(q)for i in range(256):if i == 0:if normGrayHist[i] == 0: # 0log2_0是0,但是对数在0处没有定义entropy[i] = 0else:entropy[i] = -normGrayHist[i] * math.log2(normGrayHist[i])else:if normGrayHist[i] == 0:entropy[i] = entropy[i-1] # 0log2_0是0,但是对数在0处没有定义else:entropy[i] = entropy[i-1] - normGrayHist[i] * math.log2(normGrayHist[i])# 3.找阈值fT = np.zeros([256], np.float32)ft1, ft2 = 0.0, 0.0totalEntropy = entropy[255]for i in range(255):# 找最大值ft1 = entropy[i] / zeroCumuMoment[i] + math.log2(zeroCumuMoment[i])ft2 = (entropy[255] - entropy[i]) / (1 - zeroCumuMoment[i]) + math.log2(1 - zeroCumuMoment[i])fT[i] = ft1 + ft2# 找最大值的索引,作为得到的阈值print(fT)threshLoc = np.where(fT == np.max(fT))thresh = threshLoc[0][0]# 阈值处理threshold = np.copy(image)threshold[threshold>thresh] = 255threshold[threshold<=thresh] = 0return thresh, thresholddef main():img = cv2.imread("6.jpg", 0)thresh, threshImg = thresh_entropy(img)print(thresh) # 结果是104.0titles = ['Original Image', 'After Binarization']images = [img, threshImg]for i in range(2):plt.subplot(1, 2, i + 1)plt.imshow(images[i], 'gray')plt.title(titles[i])plt.xticks([])plt.yticks([])plt.show()main()
相关文章:

图像二值化阈值调整——Triangle算法,Maxentropy方法
一. Triangle方法 算法描述:三角法求分割阈值最早见于Zack的论文《Automatic measurement of sister chromatid exchange frequency》主要是用于染色体的研究,该方法是使用直方图数据,基于纯几何方法来寻找最佳阈值,它的成立条件…...

监控视频片段合并完整视频|FFmpeg将多个视频片段拼接完整视频|PHP自动批量拼接合并视频
关于环境配置ffmpeg安装使用的看之前文章 哔哩哔哩缓存转码|FFmpeg将m4s文件转为mp4|PHP自动批量转码B站视频 <?php date_default_timezone_set("PRC"); header("Content-type: text/html; charsetutf-8"); set_time_limit(0);// 遍历获取文件 functi…...
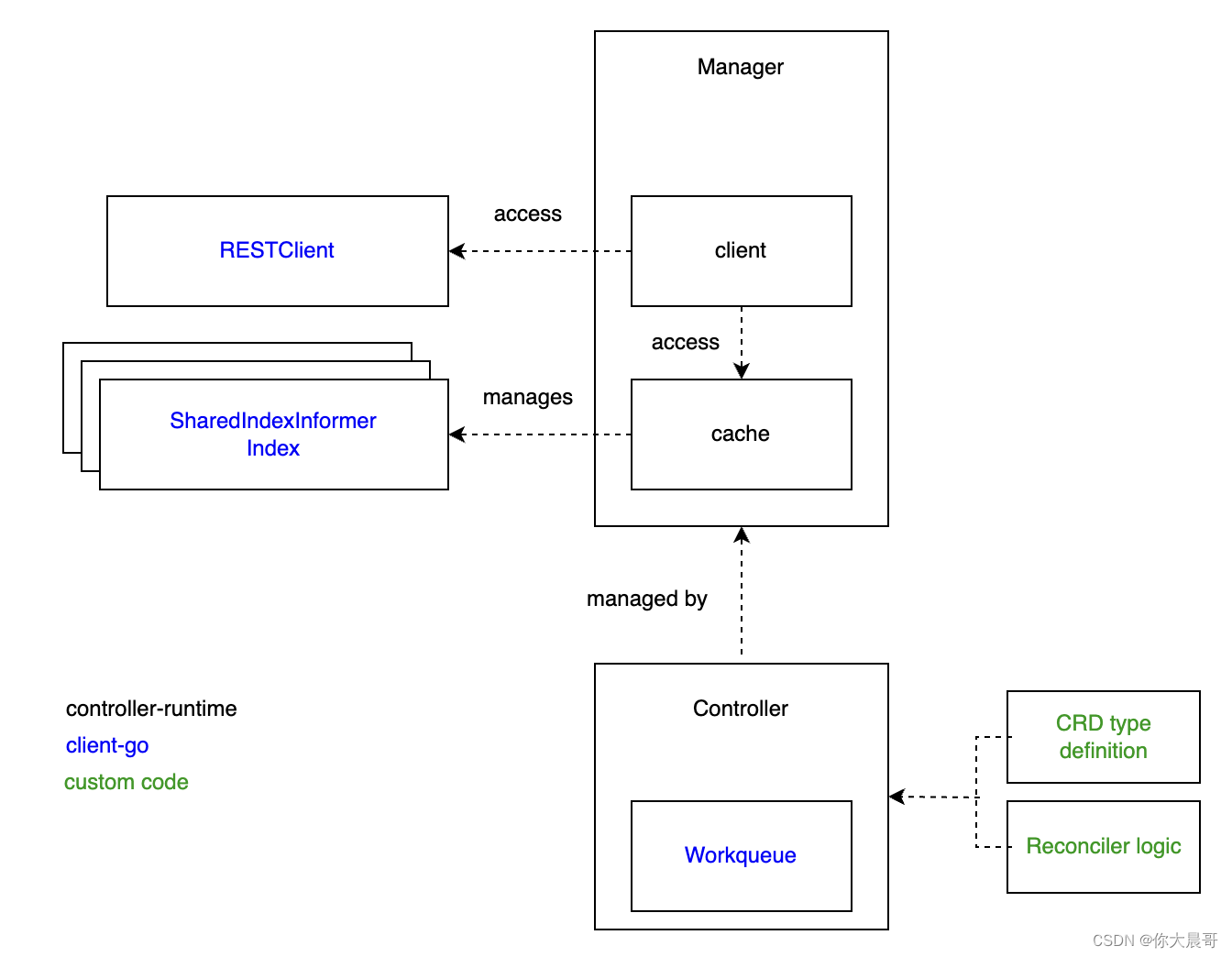
client-go controller-runtime kubebuilder
背景 这半年一直做k8s相关的工作,一直接触client-go controller-runtime kubebuilder,但是很少有文章将这三个的区别说明白,直接用框架是简单,但是出了问题就是黑盒,这不符合我的理念,所以这篇文章从头说起…...

【vue 如何解决响应式丢失】
响应式丢失原因 在 Vue 中,响应式丢失通常是由于以下原因导致的: 1. 使用非响应式对象或属性:在 Vue 中,只有使用 Vue 实例的 data 对象中的属性或使用 Vue.set() 方法添加的属性才是响应式的。如果使用普通对象或属性ÿ…...
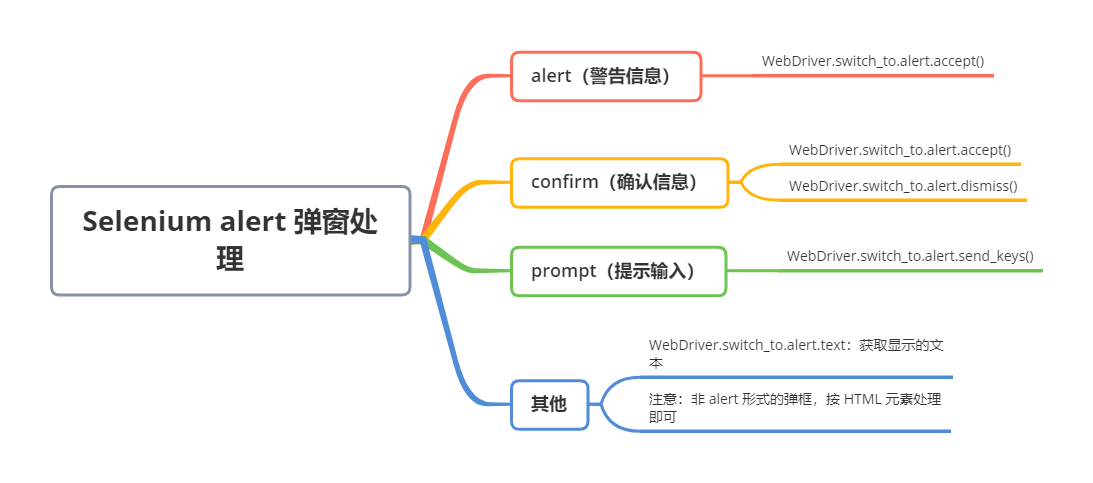
Selenium alert 弹窗处理!
页面弹窗有 3 种类型: alert(警告信息)confirm(确认信息)prompt(提示输入) 对于页面出现的 alert 弹窗,Selenium 提供如下方法: 序号方法/属性描述1accept()接受2dismis…...

有关自动化的脚本思考 python 按键 javascript
start 说来其实挺巧的,去年年中的时候,有一个同组的同事,由于工作流程需要,经常会打开某一网页,填写某些信息,然后上传特定的代码。 他有一次和我闲聊,他吐槽说,他每天的时间会被这…...

CKA认证模块②-K8S企业运维和落地实战-2
CKA认证模块②-K8S企业运维和落地实战-2 K8S常见的存储方案及具体应用场景分析 k8s存储-empty emptyDir类型的Volume是在Pod分配到Node上时被创建,Kubernetes会在Node上自动分配一个目录,因此无需指定宿主机Node上对应的目录文件。 这个目录的初始内容…...
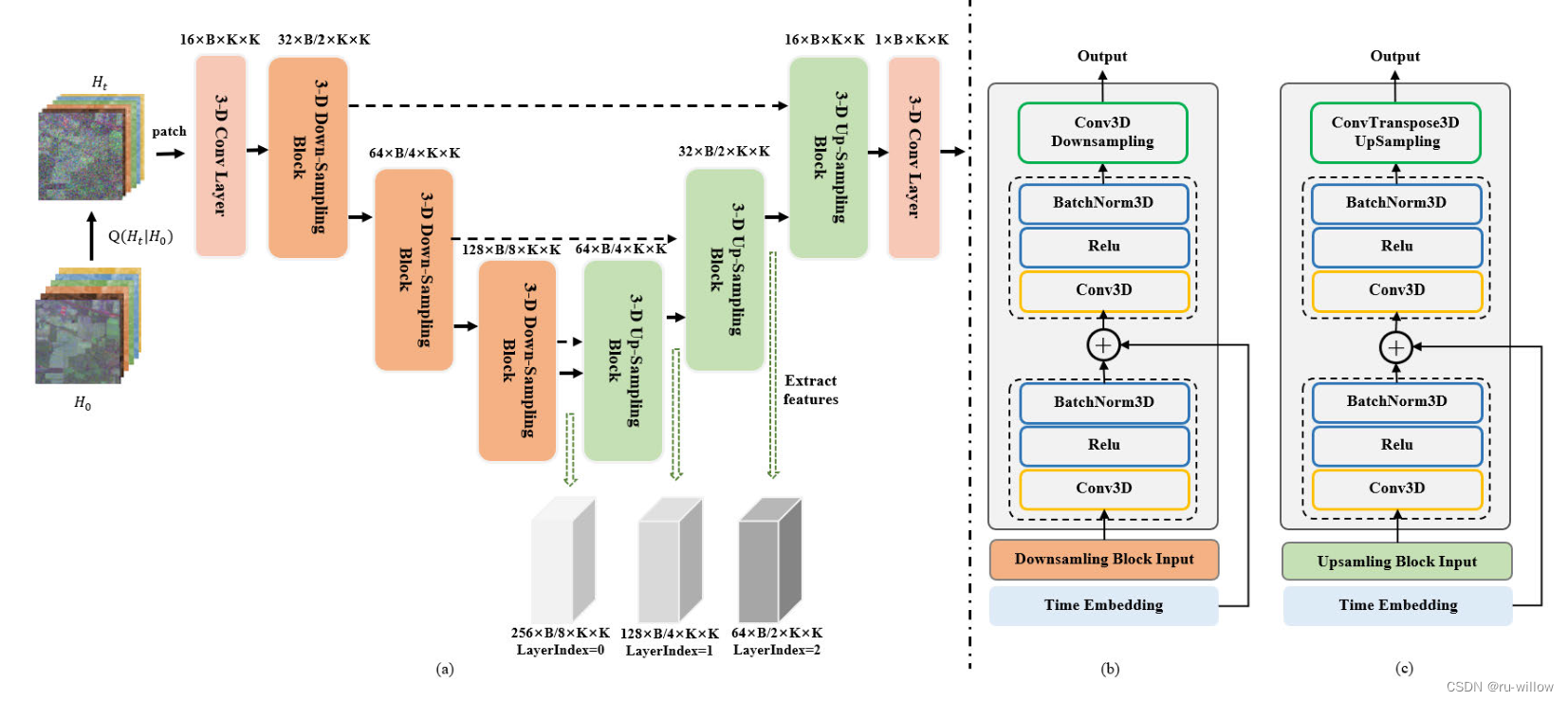
SpectralDiff论文阅读笔记
高光谱图像分类是遥感领域的一个重要问题,在地球科学中有着广泛的应用。近年来,人们提出了大量基于深度学习的HSI分类方法。然而,现有方法处理高维、高冗余和复杂数据的能力有限,这使得捕获数据的光谱空间分布和样本之间的关系具有…...
、搜索标签)
selenium基本使用、无头浏览器(chrome、FireFox)、搜索标签
selenium基本使用 这个模块:既能发请求,又能解析,还能执行js selenium最初是一个自动化测试工具,而爬虫中使用它主要是为了解决requests无法直接执行 JavaScript代码的问题 selenium 会做web方向的自动化测试appnium 会做 app方向的自动化…...
Html 引入element UI + vue3 报错Failed to resolve component: el-button
问题:Html 引入element UI vue3 ,el-button效果不出来 <!DOCTYPE html> <html> <head><meta charset"UTF-8"><!-- import Vue before Element --> <!-- <script src"https://unpkg.com/vue2/dist…...

sen2cor安装
Sen2Cor工具安装教程-百度经验 (baidu.com)...

通付盾Web3专题 | SharkTeam:Web3安全实践与创新
在Web3领域,安全漏洞、黑客攻击已愈发成为用户和投资者重点关注的领域。如何保障加密资产的安全,Web3黑暗森林中又有哪些新的攻击模式产生,SharkTeam将从一线进行分享和讨论。 我们先来看一下2023年1月到8月的安全事件数量和损失的数据统计。…...

ARM Linux 基础学习 / Ubuntu 下的包管理 / apt工具
编辑整理 by Staok。 注:在 Github 上的原版文章日后可能会更新,在其它位置发的不会跟进。文章的 Gitee 仓库地址,Gitee 访问更流畅。 Ubuntu 下的包管理 / apt工具 包管理系统的功能和优点大致相同,但打包格式和工具会因平台&a…...
springcloudalibaba入门详细使用教程
目录标题 一、简介二、SpringCloud Alibaba核心组件2-1、Nacos (配置中心与服务注册与发现)2-2、Sentinel (分布式流控)2-3、RocketMQ (消息队列)/RabbitMq/kafka2-4、Seata (分布式事务)2-5、Dubbo (RPC) 三、为什么大家看好 Spring Cloud Alibaba3-1、阿里巴巴强大的技术输出…...

C# DirectoryInfo类的用法
在C#中,DirectoryInfo类是System.IO命名空间中的一个类,用于操作文件夹(目录)。通过DirectoryInfo类,我们可以方便地创建、删除、移动和枚举文件夹。本文将详细介绍DirectoryInfo类的常用方法和属性,并提供…...
)
IDEA常用快捷键大全(详解)
如何在IDEA中进行内容全局查找 在idea中进行全局查找,可以使用快捷键“Ctrl Shift F”或者在菜单栏中选择Edit > Find > Find in Path。在弹出的界面中,输入要查找的内容。如果“Ctrl Shift F”这个快捷键无法实现全局查找,可以尝…...

设计模式之解释器模式
阅读建议 嗨,伙计!刷到这篇文章咱们就是有缘人,在阅读这篇文章前我有一些建议: 本篇文章大概5000多字,预计阅读时间长需要5分钟。本篇文章的实战性、理论性较强,是一篇质量分数较高的技术干货文章&#x…...

粉够荣获淘宝联盟区域理事会常务理事,携手共铸淘客新生态
淘宝联盟区域理事会于2021年成立,首届成立成都、广州、武汉,服务近2000个领军淘宝客企业,作为区域生态与官方交流重要枢纽,理事会举办近百场交流分享会,带动淘客跨域跨业态交流成长。 2023年9月7日第二届淘宝联盟理事…...

Python爬虫是否合法?
Python爬虫是否合法的问题颇具争议,主要涉及到使用爬虫的目的、操作方式以及是否侵犯了其他人的权益。本文将介绍Python爬虫的合法性问题,并提供一些相关的法律指导和最佳实践。 1. 什么是Python爬虫? Python爬虫是一种自动化程序ÿ…...

3.2 IDAPro脚本IDC常用函数
IDA Pro内置的IDC脚本语言是一种灵活的、C语言风格的脚本语言,旨在帮助逆向工程师更轻松地进行反汇编和静态分析。IDC脚本语言支持变量、表达式、循环、分支、函数等C语言中的常见语法结构,并且还提供了许多特定于反汇编和静态分析的函数和操作符。由于其…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...
