零基础学习Matlab,适合入门级新手,了解Matlab
一、认识Matlab
Matlab安装请参见博客 安装步骤
1.界面

2.清空环境变量及命令
(1)clear all :清除Workspace中的所有变量
(2)clc:清除Command Window中的所有命令
二、Matlab基础
1.变量命名规则
(1)变量名区分大小写;
(2)变量名长度不超过63位;
(3)变量名以字母开头,可以由字母、数字和下划线组成,但不能使用标点;
(4)变量名应简介明了,通过变量名可以直观看出变量所表示的物理意义;
2.注释
%% 注释一行,会出现横线
% 注释不出现横线

3.Matlab数据类型
(1)数字
(2)字符与字符串
(3)矩阵
%矩阵
A = [1 2 3;4 5 6 ;7 8 9]
B = A'
C = A(:) %将矩阵竖着取出来
D = inv(A) %求逆,矩阵必须为方阵




E = zeros(10,5,3) %三维度
%下面输出 E(:,:,1)表示第一维

rand、randi、randn的区别?
1.rand生成均匀分布的伪随机数。分布在(0~1)之间
主要语法:rand(m,n)生成m行n列的均匀分布的伪随机数;rand(m,n,‘double’)生成指定精度的均匀分布的伪随机数,参数还可以是‘single’;rand(RandStream,m,n)利用指定的RandStream生成伪随机数
2.randn生成标准正态分布的伪随机数(均值为0,方差为1)
主要语法:同上
3.randi生成均为分布的伪随机整数
主要语法:randi(iMax)在区间(0,iMax)生成均为分布的伪随机整数;randi(iMax,m,n)在区间(0,iMax)生成m X n型随机矩阵;randi([iMin,iMax],m,n)在区间(iMin,iMax)生成m X n型随机矩阵
E(:,:,1) = rand(10,5)
E(:,:,2) = randi(5, 10,5)
E(:,:,3) = randn(10,5)

(4)元胞数组
元胞数组是Matlab中特有的一种数据类型,是数组的一种,其内部元素可以是属于不同的数据类型,概念理解上,可以认为它和C语言里面的结构体、C++里面的对象很类似。它特有的存取数据方法决定了它的特点,它有给人一种查询信息的感觉,可以逐渐追踪一直到所有的变量全部翻译成基本的数据信息。
A = cell(1, 6)

A{2} = eye(3)

magic字面意思是魔方,魔术的意思。在matlab中用来生成n阶幻方。比如三阶幻方就是1-9九个数字,组成一个3*3的矩阵,使得该矩阵无论横、竖还是斜三个方向上的三个数的总和是相同的。
A{5} = magic(5)


B = A{5}

(5)结构体
books = struct('name',{{'Machine Learing','Data Mining'}},'price',[30 40])
books.name
books.name(1) % 元胞数组
books.name{1} %字符串

4.矩阵定义与构造
A = [1 2 3 5 8 8 4 6]
B = 1:2:9
C = repmat(B,3,1)
D = ones(2,4)

5.矩阵的四则运算
A = [1 2 3 4;5 6 7 8]
B = [1 1 2 2;2 2 1 1]
C = A + B
D = A - B
E = A * B'
F = A .* B %对应项相乘
G = A / B %相当于A乘B的逆
H = A ./ B %对应项相除

6.矩阵的下标
A = magic(5)
B = A(2,3)
C = A(3,:) %第三行
D = A(:,4) %第四列
[m,n] = find(A > 20) %找大于20的序号值/矩阵,取出索引值

三、Matlab绘图
1.二维平面绘图1
x = 0:0.01:2*pi;
y = sin(x);
figure %建立一个幕布
plot(x,y)
title('y = sin(x)')
xlabel('x')
ylabel('sin(x)')
xlim([0 2*pi]) %x轴的取值范围

2.二维平面绘图2
x = 0:0.01:20;
y1 = 200*exp(-0.05*x).*sin(x)
y2 = 0.8*exp(-0.5*x).*sin(10*x)
figure
[AX,H1,H2] = plotyy(x,y1,x,y2,'plot');%共用一个x轴
set(get(AX(1),'Ylabel'),'String','Slow Decay')
set(get(AX(2),'Ylabel'),'String','Fast Decay')
xlabel('Time(\musec)')
title('Multiple Deacy Rates')
set(H1,'LineStyle','--')
set(H2,'LineStyle',':')

3.三维立体绘图
t = 0:pi/50:10*pi;
plot3(sin(t),cos(t),t) %三维绘图用plot3
xlabel('sin(t)')
ylabel('cos(t)')
zlabel('t')
grid on %添加网格线
axis square

%双峰模型
[x,y,z] = peaks(30);
mesh(x,y,z)
grid

四、Matlab图像的导出









相关文章:

零基础学习Matlab,适合入门级新手,了解Matlab
一、认识Matlab Matlab安装请参见博客 安装步骤 1.界面 2.清空环境变量及命令 (1)clear all :清除Workspace中的所有变量 (2)clc:清除Command Window中的所有命令 二、Matlab基础 1.变量命名规则 &a…...

CCF ChinaSoft 2023 论坛巡礼 | 自动驾驶仿真测试论坛
2023年CCF中国软件大会(CCF ChinaSoft 2023)由CCF主办,CCF系统软件专委会、形式化方法专委会、软件工程专委会以及复旦大学联合承办,将于2023年12月1-3日在上海国际会议中心举行。 本次大会主题是“智能化软件创新推动数字经济与社…...

vue封装useWatch hook支持停止监听和重启监听功能
import { watch, reactive } from vue;export function useWatch(source, cb, options) {const state reactive({stop: null});function start() {state.stop watch(source, cb, options);}function stop() {state.stop();state.stop null;}// 返回一个对象,包含…...

智能配方颗粒管理系统解决方案,专业实现中医药产业数字化-亿发
“中药配方颗粒”,又被称为免煎中药,源自传统中药饮片,经过提取、分离、浓缩、干燥、制粒、包装等工艺加工而成。这种新型配方药物完整保留了原中药饮片的所有特性。既能满足医师的辨证论治和随症加减需求,同时具备强劲好人高效的…...
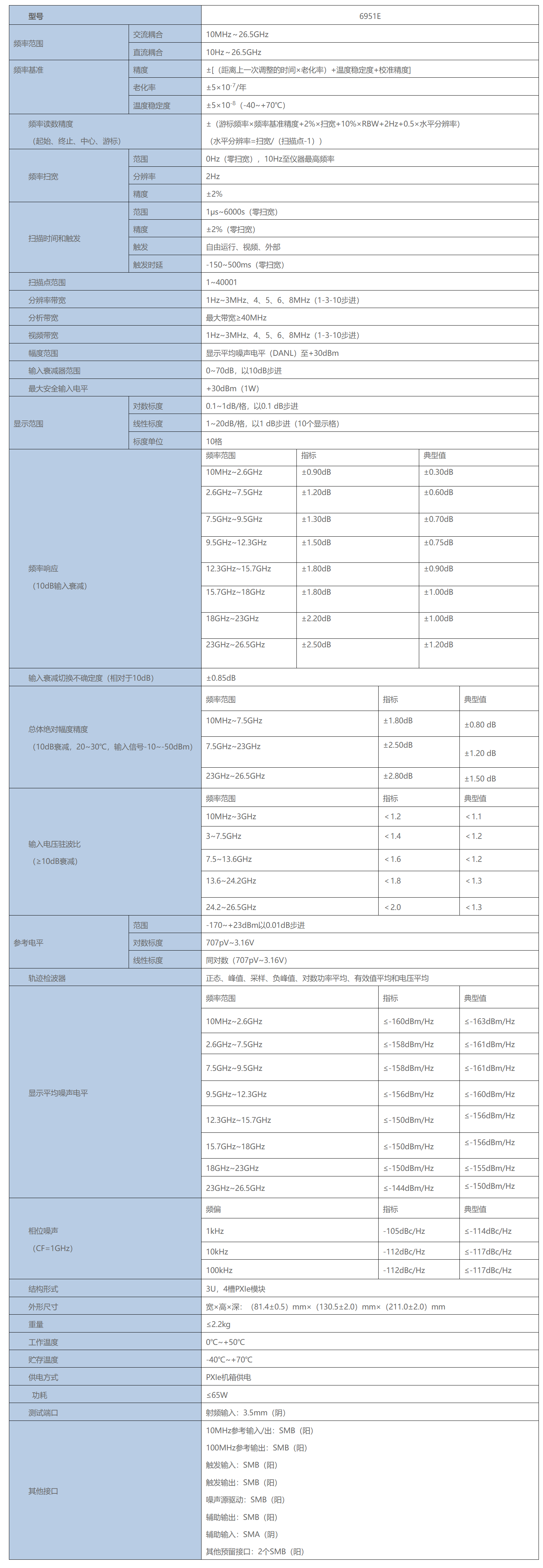
PXI总线测试模块-6951E 信号分析仪
6951E 信号分析仪 频率范围:10Hz~26.5GHz 6951E信号分析仪率范围覆盖10Hz~26.5GHz、带宽40MHz,具备频谱分析、相邻信道功率测试、模拟解调、噪声系数测试等多种测量功能。 6951E信号分析仪采用PXIe总线3U 4槽结构形式ÿ…...

精确杂草控制植物检测模型的改进推广
Improved generalization of a plant-detection model for precision weed control 摘要1、介绍2、结论摘要 植物检测模型缺乏普遍性是阻碍实现自主杂草控制系统的主要挑战之一。 本文研究了训练和测试数据集分布对植物检测模型泛化误差的影响,并使用增量训练来减小泛化误差。…...
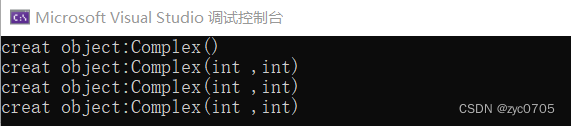
C++:对象成员方法的使用
首先复习一下const : //const: //Complex* const pthis1 &ca; //约束指针自身 不能指向其他对象 // pthis1 &cb; err //pthis1->real; //const Complex* const pthis1 &ca;//指针指向 指针自身 都不能改 //pthis1->real; 只可读 …...
深入了解SpringMvc接收数据
目录 一、访问路径(RequestMapping) 1.1 访问路径注解作用域 1.2 路径精准(模糊)匹配 1.3 访问路径限制请求方式 1.4 进阶访问路径请求注解 1.5 与WebServlet的区别 二、接收请求数据 2.1 请求param参数 2.2 请求路径参数 2.3 请求…...

华东“启明”青少年音乐艺术实践中心揭幕暨中国“启明”巴洛克合奏团首演音乐会
2023年11月11日,华东“启明”青少年音乐艺术实践中心在上海揭幕,中国“启明”巴洛克合奏团开启了首场音乐会。 华东“启明”青少年音乐艺术实践中心由中共宁波市江北区委宣传部与上音管风琴艺术中心联合指导,宁波音乐港、宁波市江北区洛奇音乐…...

17. 机器学习——SVM
机器学习面试题汇总与解析——SVM 本章讲解知识点 什么是 SVMSVM 的基本原理线性不可分 SVM非线性 SVMSVM 优缺点本专栏适合于Python已经入门的学生或人士,有一定的编程基础。 本专栏适合于算法工程师、机器学习、图像处理求职的学生或人士。 本专栏针对面试题答案进行了优化…...

算法导论笔记5:贪心算法
P216 第15章动态规划 最优子结构 具有它可能意味着适合应用贪心策略 动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法。 剪切-粘贴技术证明 每个子问题的解就是它本身的最优解(利用反证法࿰…...

Vue的高级表格组件库【vxe-table】
文章目录 前言vxe-table官网实现表头拖拽树形表格全键盘操作后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:前端系列文章 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板…...

从0到0.01入门React | 002.精选 React 面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…...

假冒 Skype 应用程序网络钓鱼分析
参考链接: https://slowmist.medium.com/fake-skype-app-phishing-analysis-35c1dc8bc515 背景 在Web3世界中,涉及假冒应用程序的网络钓鱼事件相当频繁。慢雾安全团队此前曾发表过分析此类网络钓鱼案例的文章。由于Google Play在中国无法访问,许多用户…...
软件外包开发的需求表达方法
软件开发需求的有效表达对于项目的成功至关重要。无论选择哪种需求表达方法,清晰、详细、易于理解是关键。与开发团队建立良好的沟通渠道,确保他们对需求有充分的理解,并随着项目的推进及时调整和更新需求文档。以下是一些常用的需求表达方法…...
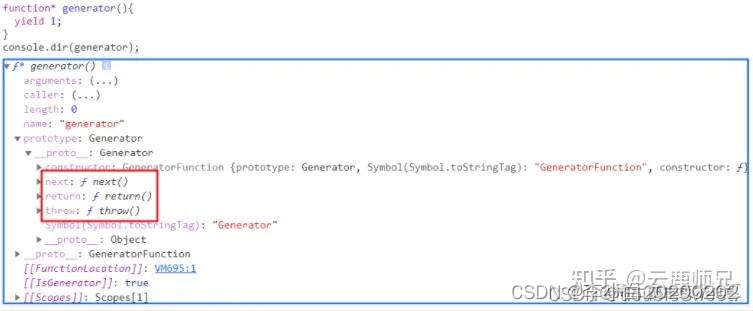
详解JS的四种异步解决方案:回调函数、Promise、Generator、async/await
同步&异步的概念 在讲这四种异步方案之前,我们先来明确一下同步和异步的概念: 所谓同步(synchronization),简单来说,就是顺序执行,指的是同一时间只能做一件事情,只有目前正在执行的事情做完之后&am…...

Python进行多线程爬取数据通用模板
首先,我们需要导入所需的库,包括requests和BeautifulSoup。requests库用于发送HTTP请求,BeautifulSoup库用于解析HTML文档。 import requests from bs4 import BeautifulSoup然后,我们需要定义一个函数来发送HTTP请求并返回响应。…...
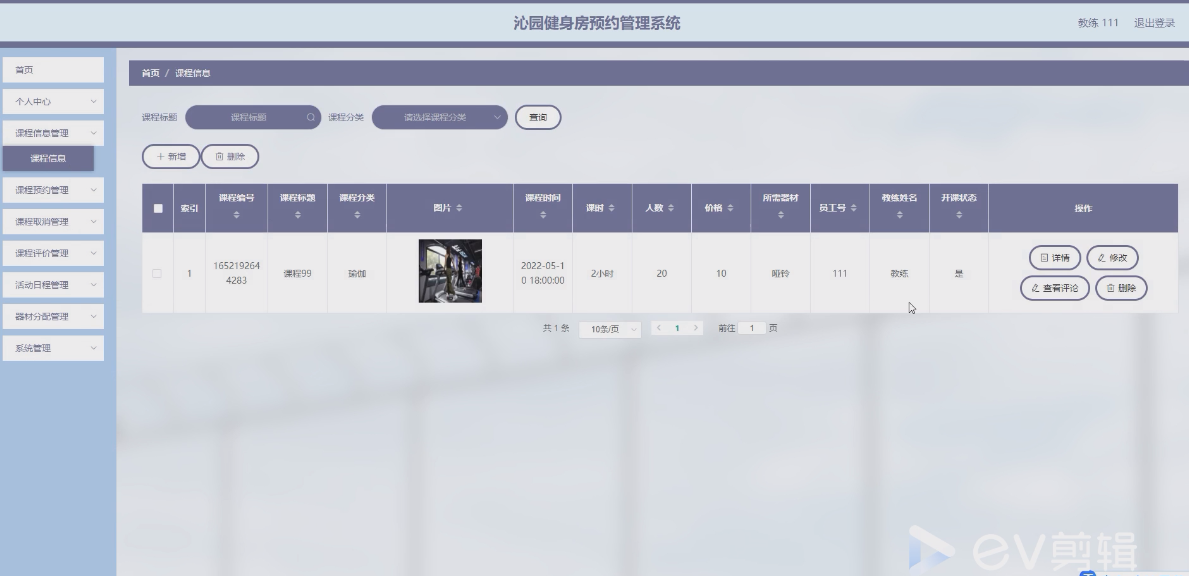
基于springboot实现沁园健身房预约管理系统【项目源码】
基于springboot实现沁园健身房预约管理系统演示 B/S架构 B/S结构是目前使用最多的结构模式,它可以使得系统的开发更加的简单,好操作,而且还可以对其进行维护。使用该结构时只需要在计算机中安装数据库,和一些很常用的浏览器就可以…...

论文笔记:Deep Trajectory Recovery with Fine-Grained Calibration using Kalman Filter
TKDE 2021 1 intro 1.1 背景 用户轨迹数据对于改进以用户为中心的应用程序很有用 POI推荐城市规划路线规划由于设备和环境的限制,许多轨迹以低采样率记录 采样的轨迹无法详细说明物体的实际路线增加了轨迹中两个连续采样点之间的不确定性——>开发有效的算法以…...

ubuntu下tensorrt环境配置
文章目录 一、Ubuntu18.04环境配置1.1 安装工具链和opencv1.2 安装Nvidia相关库1.2.1 安装Nvidia显卡驱动1.2.2 安装 cuda11.31.2.3 安装 cudnn8.21.2.4 下载 tensorrt8.4.2.4 二、编写CMakeLists.txt三、TensorRT系列教程 一、Ubuntu18.04环境配置 教程同样适用与ubuntu22.04…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
