【数据结构】非递归实现二叉树的前 + 中 + 后 + 层序遍历(听说面试会考?)

👦个人主页:@Weraphael
✍🏻作者简介:目前学习C++和算法
✈️专栏:数据结构
🐋 希望大家多多支持,咱一起进步!😁
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 📂 加关注✨
目录
- 一、需要使用到的代码
- 1.1 二叉树的基本实现
- 1.2 栈
- 1.3 队列
- 二、非递归实现二叉树的前序遍历
- 2.1 思路
- 2.2 代码实现
- 三、非递归实现二叉树的前序遍历
- 3.1 思路
- 3.2 代码实现
- 四、后序遍历
- 4.1 思路
- 4.2 代码实现
- 五、层序遍历
- 5.1 思路
- 5.2 代码实现
- 5.3 整个测试结果
- 六、总结
一、需要使用到的代码
1.1 二叉树的基本实现
二叉树的基本实现在以往博客已经详细讨论过了,这里直接给出本篇博客的所需用到的源代码。【数据结构】二叉树的链式结构(笔记总结)
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>typedef int DataType;typedef struct BinaryTree
{DataType _data;struct BinaryTree *_left;struct BinaryTree *_right;
} BinaryTree;// 创建结点
BinaryTree *CreateNode(DataType x)
{BinaryTree *newnode = (BinaryTree *)malloc(sizeof(BinaryTree));if (newnode == NULL){printf("CreateNode failed\n");return NULL;}newnode->_left = NULL;newnode->_right = NULL;newnode->_data = x;return newnode;
}// 建树
BinaryTree *CreateTree()
{// 假定树的模型如下所示// 1// 2 3// 4 5 6BinaryTree *node1 = CreateNode(1);BinaryTree *node2 = CreateNode(2);BinaryTree *node3 = CreateNode(3);BinaryTree *node4 = CreateNode(4);BinaryTree *node5 = CreateNode(5);BinaryTree *node6 = CreateNode(6);node1->_left = node2;node1->_right = node3;node2->_left = node4;node2->_right = node5;node3->_right = node6;return node1;
}// 递归实现前序遍历
void PreOrder(BinaryTree *root)
{if (root == NULL)return;printf("%d ", root->_data);PreOrder(root->_left);PreOrder(root->_right);
}// 递归实现中序遍历
void InOrder(BinaryTree *root)
{if (root == NULL)return;InOrder(root->_left);printf("%d ", root->_data);InOrder(root->_right);
}// 递归实现后序遍历
void PostOrder(BinaryTree *root)
{if (root == NULL)return;PostOrder(root->_left);PostOrder(root->_right);printf("%d ", root->_data);
}
在以上源代码中,我另外给出了递归实现遍历的版本,目的是为了和非递归(迭代)版进行对比。
1.2 栈
// 需要存储的数据类型是二叉树结构体的指针!
typedef BinaryTree *DataType1;typedef struct stack
{DataType1 *_a;int size;int capacity;
} stack;void StackInit(stack *st)
{st->_a = (DataType1 *)malloc(sizeof(DataType1) * 4); // 假设默认大小为4if (st->_a == NULL){printf("st->_a malloc failed\n");return;}st->capacity = 4;st->size = 0;
}// 入栈
void PushStack(stack *st, DataType1 val)
{if (st->capacity == st->size){// 每次扩大两倍DataType1 *newcapacity = (DataType1 *)realloc(st->_a, sizeof(DataType1) * 4 * 2); if (newcapacity == NULL){printf("st->_a realloc failed\n");return;}st->_a = newcapacity;st->capacity *= 2;}st->_a[st->size] = val;st->size++;
}// 判断栈是否为空
bool StackEmpty(stack *st)
{return st->size == 0;
}// 出栈
void PopStack(stack *st)
{if (StackEmpty(st)){printf("stack is empty\n");return;}st->size--;
}// 访问栈顶元素
DataType1 StackTop(stack *st)
{return st->_a[st->size - 1];
}
栈是后面前、中、后序遍历所需要的。但是需要注意的是:栈需要存储的数据类型是二叉树结构体的指针。为什么?在后面会详细说明。
1.3 队列
// 需要存储的数据类型是二叉树结构体的指针
typedef BinaryTree *QueueType;
typedef struct QueueNode
{QueueType _val;struct QueueNode *_next;
} QueueNode;typedef struct Queue
{QueueNode *tail;QueueNode *head;
} Queue;// 初始化队列
void InitQueue(Queue *q)
{q->tail = q->head = NULL;
}// 插入元素
void PushQueue(Queue *q, QueueType x)
{QueueNode *newnode = (QueueNode *)malloc(sizeof(QueueNode));if (newnode == NULL){printf("newnode create failed\n");return;}newnode->_next = NULL;newnode->_val = x;if (q->head == NULL){if (q->tail != NULL)return;q->head = q->tail = newnode;}else{q->tail->_next = newnode;q->tail = newnode;}
}// 判断队列是否为空
bool QueueEmpty(Queue *q)
{return (q->head == NULL) && (q->tail == NULL);
}// 队头元素
QueueType FrontQueue(Queue *q)
{return q->head->_val;
}// 出队列
void PopQueue(Queue *q)
{if (QueueEmpty(q)){printf("Queue is empty\n");return;}if (q->head->_next == NULL){free(q->head);q->head = q->tail = NULL;}else{QueueNode *next = q->head->_next;free(q->head);q->head = next;}
}
队列是为层序遍历所准备的。同理地,队列存储的数据类型同样也要是二叉树结构体指针。
为了快速实现二叉树的遍历,以上栈和队列的细节代码并不完整。详细的可以参考往期博客:点击跳转
话不多说,现在进入正题!
二、非递归实现二叉树的前序遍历
2.1 思路
请看下图
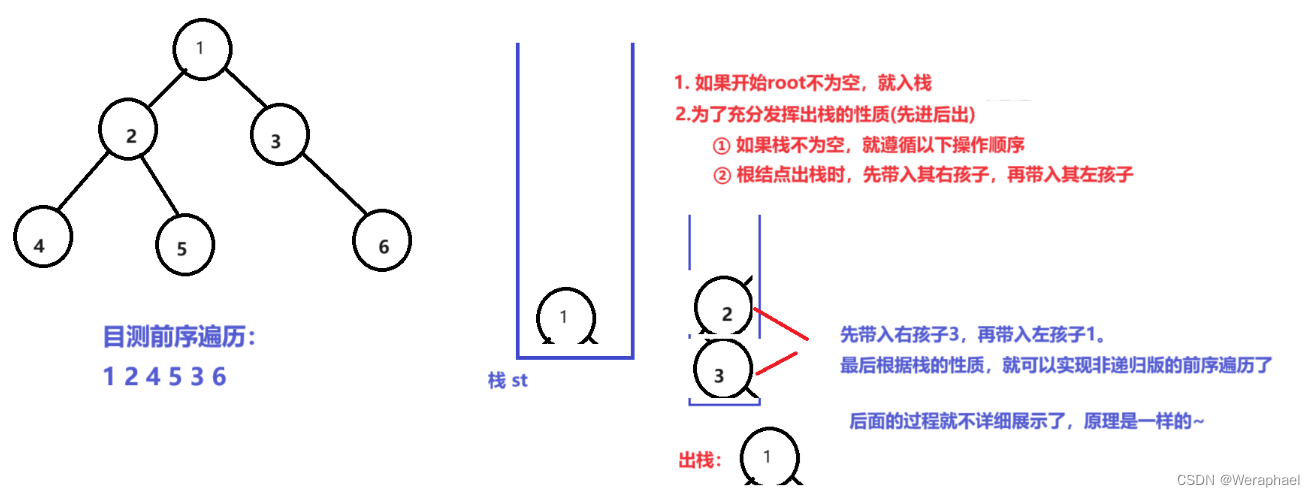
最后回过头来讲讲为什么栈的存储的类型要是二叉树结构体的指针?
通过上图,我们总结了:结点出栈,需要带入其左右孩子。因此,如果不是其结构体指针,那么也就无法将root的左右孩子入栈了。注意:也不能存结构体。因为一个结构体太大了,而指针的大小只有4/8字节
2.2 代码实现
// 非递归实现前序遍历
void PreOrder_nonR(BinaryTree *root)
{// 1. 需要一个赋值栈stack st;StackInit(&st);// 2. 如果根结点不为空入栈if (root != NULL){PushStack(&st, root);}while (!StackEmpty(&st)){// 记录栈顶元素BinaryTree *top = StackTop(&st);// 3. 出栈后带入其左右孩子PopStack(&st);printf("%d ", top->_data);// !要注意顺序:先带右孩子,再带左孩子 if (top->_right)PushStack(&st, top->_right);if (top->_left)PushStack(&st, top->_left);}
}
三、非递归实现二叉树的前序遍历
3.1 思路
请看下图
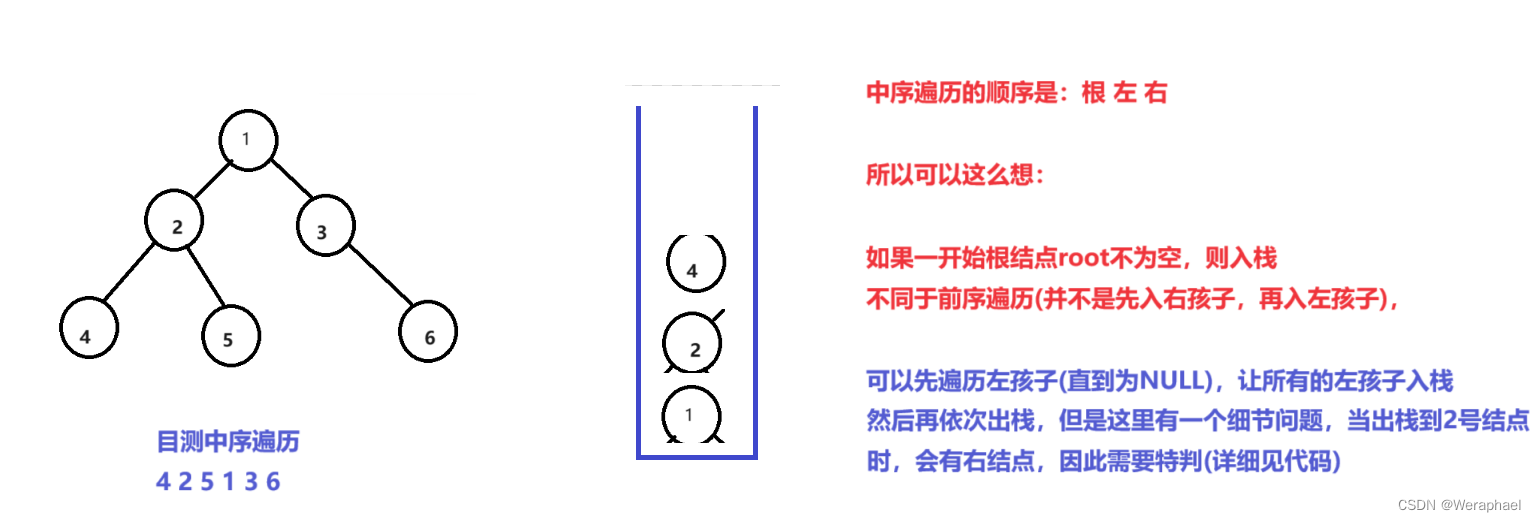
3.2 代码实现
void InOrder_nonR(BinaryTree *root)
{// 1. 需要一个辅助栈stack st;StackInit(&st);// 如果一开始根结点为NULL// 直接返回if (root == 0)return;// 2.遍历左孩子,将其全部入栈BinaryTree *cur = root;while (cur){PushStack(&st, cur);cur = cur->_left;}while (!StackEmpty(&st)){// 出栈打印BinaryTree *top = StackTop(&st);PopStack(&st);printf("%d ", top->_data);// 特判:出栈结点存在右孩子if (top->_right){// 将其入栈PushStack(&st, top->_right);// 然后还要特殊判断这个右孩子有没有左孩子// 因为我们要保证 先左 再根 再右BinaryTree *cur2 = top->_right;while (cur2->_left){PushStack(&st, cur2->_left);cur2 = cur2->_left;}}}
}
四、后序遍历
4.1 思路
后序遍历我就不画图了,本人一开始写非递归后序遍历写了好久,都失败了(太菜了)。直到我看到一个视频,才知道原来后序遍历这么简单!
首先可以参考前序遍历(根左右)。因此,我们只要将前序遍历的代码逻辑的遍历顺序左和右对调一下,就变成根右左,最后再对其逆序,就是左右根,也就是后序遍历的结果了
4.2 代码实现
void PostOrder_nonR(BinaryTree *root)
{int res[6]; // 为了逆序int i = 0; // 用于遍历res数组memset(res, 0, sizeof(int));stack st;StackInit(&st);if (root != NULL){PushStack(&st, root);}while (!StackEmpty(&st)){BinaryTree *top = StackTop(&st);PopStack(&st);res[i++] = top->_data;// 将前序遍历的代码逻辑的遍历顺序对调if (top->_left)PushStack(&st, top->_left);if (top->_right)PushStack(&st, top->_right);}// 最后逆序输出即可for (int k = i - 1; k >= 0; k--){printf("%d ", res[k]);}printf("\n");
}
五、层序遍历
5.1 思路
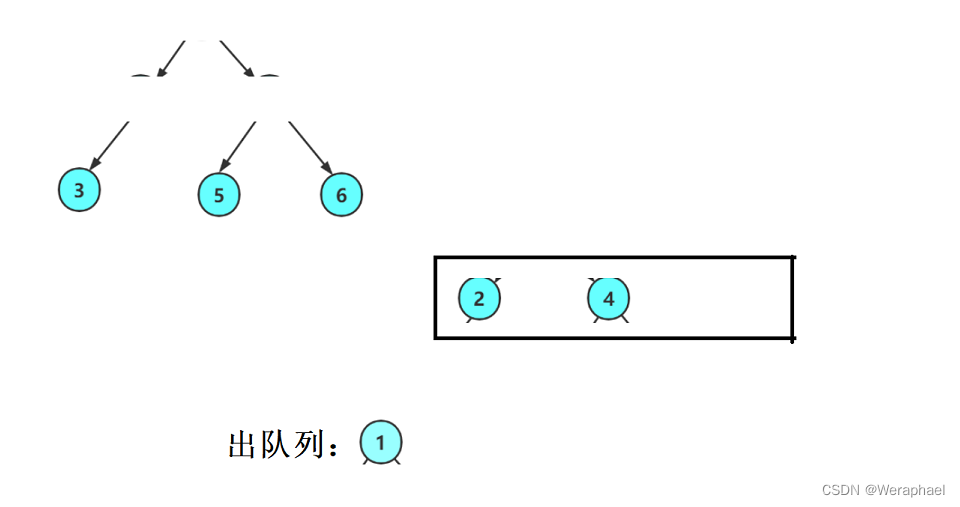
层序遍历顾名思义就是一层一层遍历,那么就不能使用栈,得使用队列。
步骤:使用一个队列,出一个结点,带入它的孩子结点
如果树不为空,就先让根结点入队列
然后出队列(打印
1),再把1的左孩子和右孩子带入队列
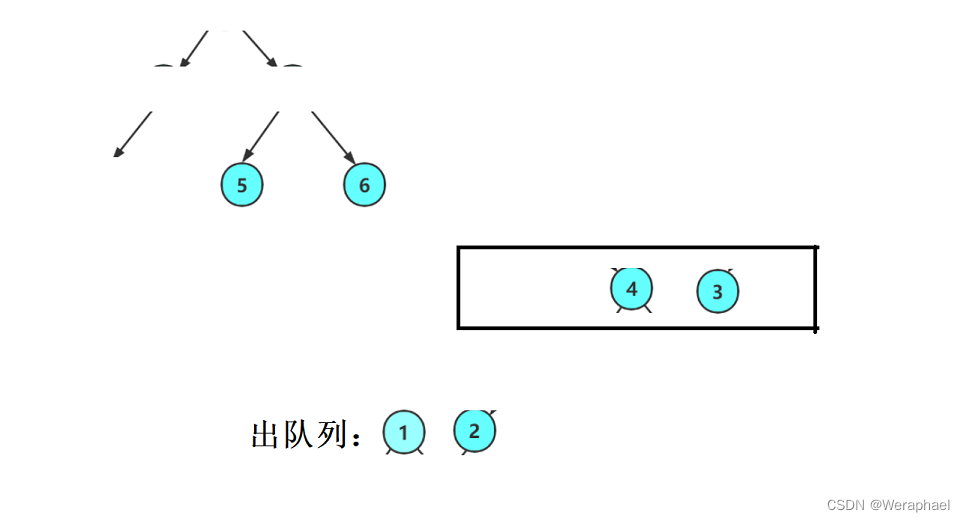
接着让
2出队列,再把2的孩子入队列
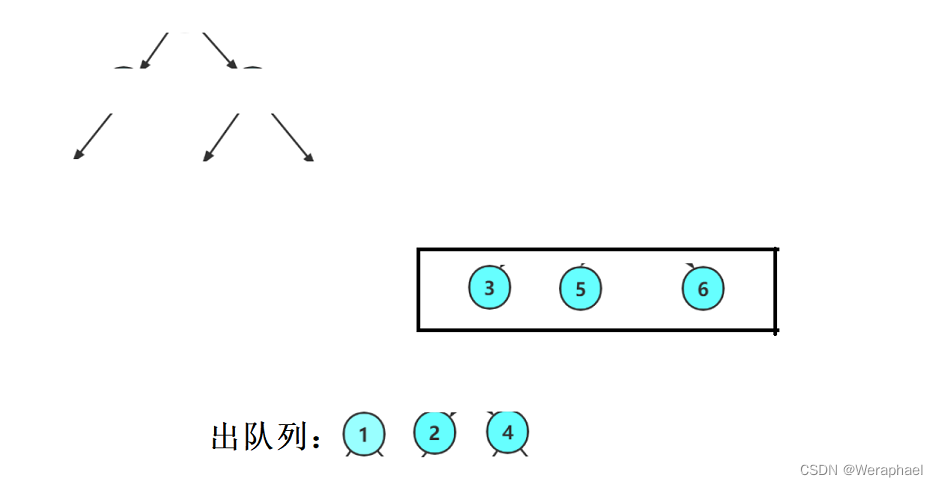
同理,再让
4出队列,把它的孩子入队列
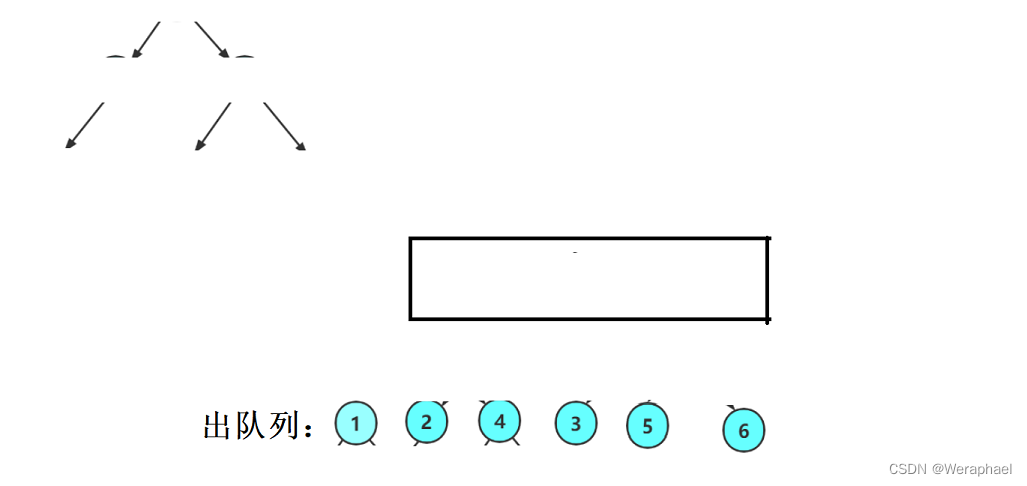
最后如果队列为空,即完成层序遍历
5.2 代码实现
void LevelOrder(BinaryTree *root)
{// 1. 需要辅助队列Queue q;InitQueue(&q);// 如果一开始根结点root不为空// 则入队列if (root != NULL)PushQueue(&q, root);// 然后出双亲结点,带入子结点while (!QueueEmpty(&q)){BinaryTree *front = FrontQueue(&q);PopQueue(&q);printf("%d ", front->_data);// 带入子结点if (front->_left)PushQueue(&q, front->_left);if (front->_right)PushQueue(&q, front->_right);}
}
5.3 整个测试结果

六、总结
对于数据结构,还是得建议多画画图。最后我不将所有的代码整合到一块,读者只需理解,最好自己实现一遍。
相关文章:

【数据结构】非递归实现二叉树的前 + 中 + 后 + 层序遍历(听说面试会考?)
👦个人主页:Weraphael ✍🏻作者简介:目前学习C和算法 ✈️专栏:数据结构 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞&…...

32 Feign性能优化
2.3.Feign使用优化 Feign底层发起http请求,依赖于其它的框架。其底层客户端实现包括: •URLConnection:默认实现,不支持连接池 •Apache HttpClient :支持连接池 •OKHttp:支持连接池 因此提高Feign的…...

星岛专栏|从Web3发展看金融与科技的融合之道
11月起,欧科云链与香港主流媒体星岛集团开设Web3.0安全技术专栏,该专栏主要面向香港从业者、交易机构、监管机构输出专业性的安全合规建议,旨在促进香港Web3.0行业向安全与合规发展。 出品|欧科云链研究院 自2016年首届香港金融…...

什么是网络爬虫?
网络爬虫是一种自动化程序,可以自动地浏览网站并从网站上抽取数据。APP数据抓取实际上也是运用了网络爬虫的技术,只不过抓取的对象不是网站上的信息,而是手机APP上的数据。下面详细介绍APP数据抓取的过程。 1、确定数据需求 首先需要明确要抓…...
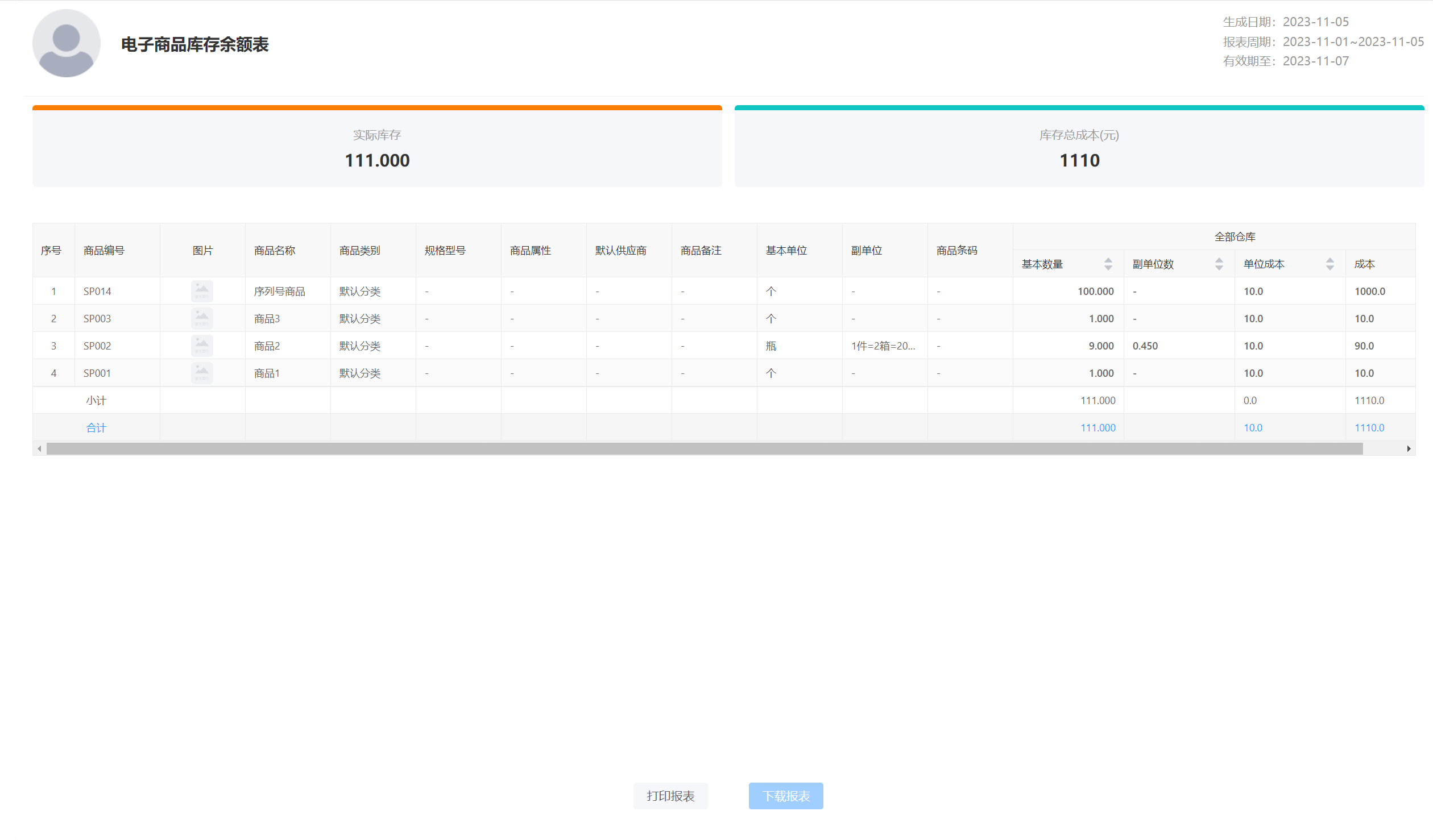
酷柚易汛ERP - 商品库存余额表操作指南
1、应用场景 商品库存余额表用于查询商品在各仓库的实际结存量、单位成本以及成本等明细。 2、主要操作 打开【仓库】-【商品库存余额表】,可筛选仓库、商品、商品类别,导出/打印等操作见【销货单】不再赘述。 3、分享操作 库存余额分享,…...

第27期 | GPTSecurity周报
GPTSecurity是一个涵盖了前沿学术研究和实践经验分享的社区,集成了生成预训练Transformer(GPT)、人工智能生成内容(AIGC)以及大型语言模型(LLM)等安全领域应用的知识。在这里,您可以…...

大数据-玩转数据-Flume
一、Flume简介 Flume提供一个分布式的,可靠的,对大数据量的日志进行高效收集、聚集、移动的服务,Flume只能在Unix环境下运行。Flume基于流式架构,容错性强,也很灵活简单。Flume、Kafka用来实时进行数据收集,Spark、Flink用来实时处理数据,impala用来实时查询。二、Flume…...

【Linux】进程概念IV 进程地址空间
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法…感兴趣就关注我吧!你定不会失望。 本篇导航 0. 数据在内存中的分布1. 虚拟地址与真实物理地址2. 进程地址空间2.1 进程地址空间概念2.2 进程->页表->内存 0. 数据在内…...

Flink在汽车行业的应用【面试加分系列】
很多同学问我为什么要发这些大数据前沿汇报? 一方面是自己学习完后觉得非常好,然后总结发出来方便大家阅读;另外一方面,看这些汇报对你的面试帮助会很大,特别是面试前可以看看即将面试公司在大数据前沿的发展动向&…...
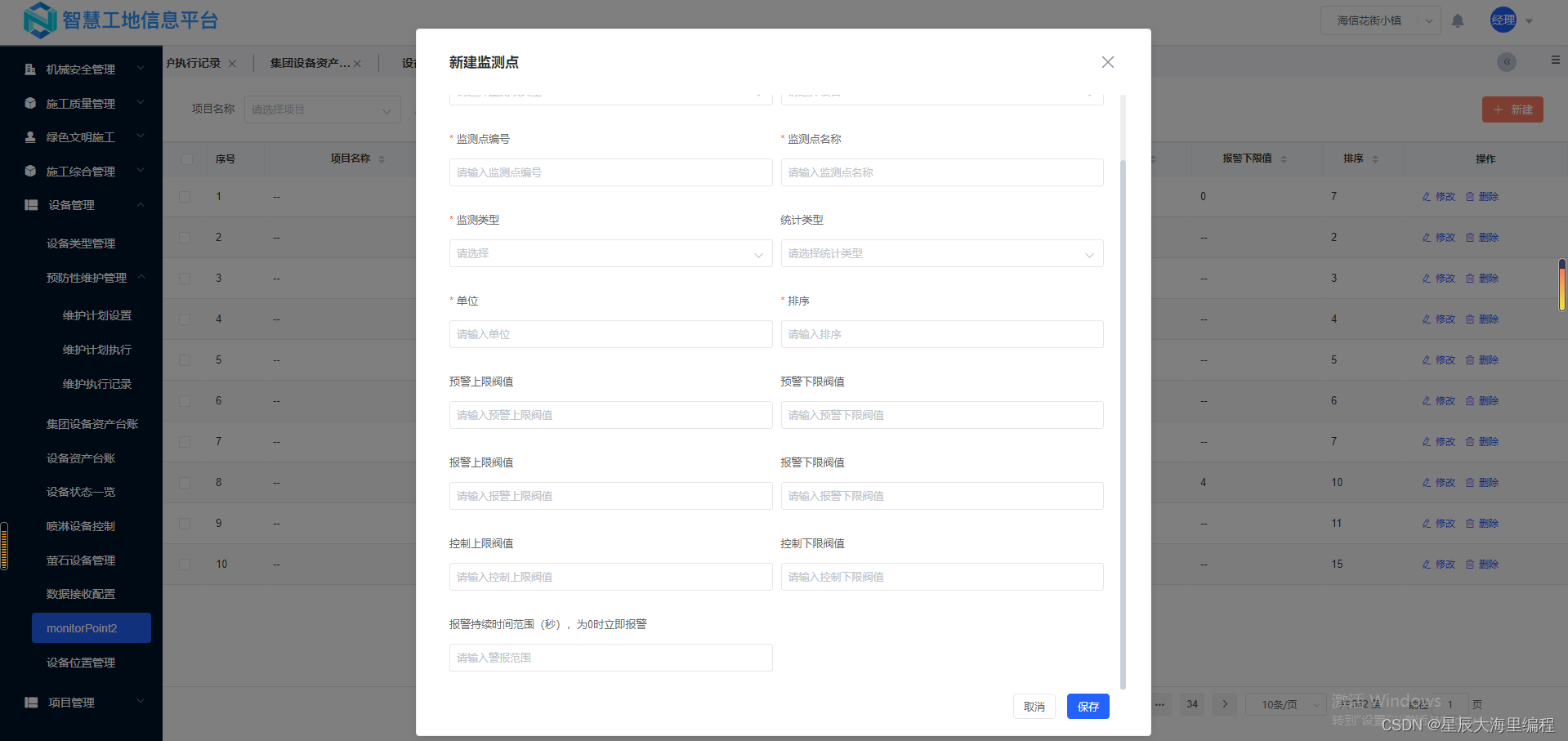
智慧工地源码:助力数字建造、智慧建造、安全建造、绿色建造
智慧工地围绕建设过程管理,建设项目与智能生产、科学管理建设项目信息生态系统集成在一起,该数据在虚拟现实环境中,将物联网收集的工程信息用于数据挖掘和分析,提供过程趋势预测和专家计划,实现工程建设的智能化管理&a…...

Spring Boot(二)
1、运行维护 1.1、打包程序 SpringBoot程序是基于Maven创建的,在Maven中提供有打包的指令,叫做package。本操作可以在Idea环境下执行。 mvn package 打包后会产生一个与工程名类似的jar文件,其名称是由模块名版本号.jar组成的。 1.2、程序…...
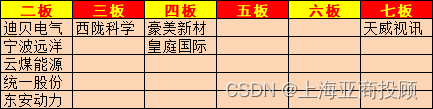
上海亚商投顾:沪指缩量调整跌 高位强势股继续退潮
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪 三大指数11月10日弱势震荡,上证50盘中跌超1%,以保险为首的权重板块走势较弱。 高位强…...

药理学试卷
1【单选题】关于尼可刹米,错误的是 C A、直接兴奋延脑呼吸中枢 B、刺激颈动脉体化学感受器 C、作用时间较长 D、过量可致惊厥 2【单选题】属于第三代头孢菌素的药物是 C A、头孢克洛 B、头孢噻吩 C、头孢曲松 D、头孢匹罗 3【单选题】不属于β受体阻断药禁…...

SpringBoot3-快速入门
1.前置知识 Java17Spring、SpringMVC、MyBatisMaven、IDEA\ 2. 环境要求 环境&工具 版本(or later) SpringBoot 3.0.5 IDEA 2021.2.1 Java 17 Maven 3.5 Tomcat 10.0 Servlet 5.0 GraalVM Community 22.3 Native Build Tools 0.9…...

具名挂载和匿名挂载
匿名卷挂载 : -v 的时候只指定容器内的路径 如下面这个:/etc/nginx 1.docker run -d -P --name nginx -v /etc/nginx nginx 2.查看所有卷 docker volume ls 这里发现,这就是匿名挂载,只指定容器内的路径,没有指定…...
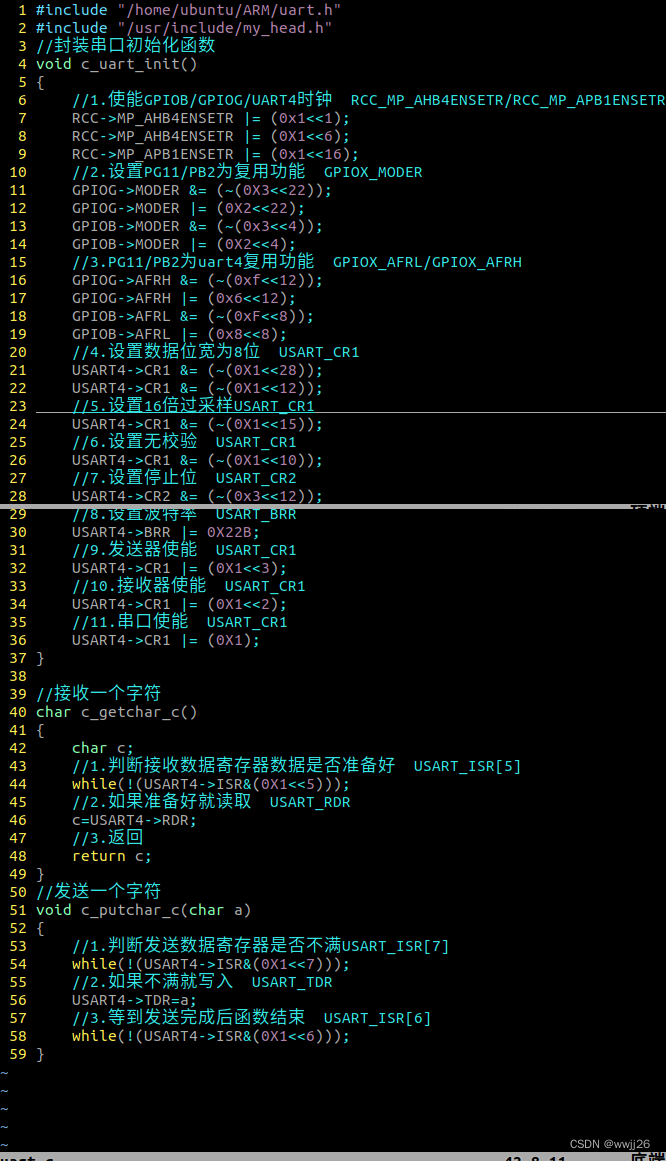
ARM串口
...
)
C++ Qt 学习(文章链接汇总)
C Qt 学习(一):Qt 入门 C Qt 学习(二):常用控件使用与界面布局 C Qt 学习(三):无边框窗口设计 C Qt 学习(四):自定义控件与 qss 应用 …...

2311d9月会议
DLF2023年9月月度会议摘要 Robert Robert,在DConf上做了一些初步的JSON5工作.他还更新了Bugzilla到GitHub的迁移脚本.他使用了"隐藏"API,现在脚本要快得多. 除此外,他在DScanner上做了一些小事,并等待JanJurzitza(Webfreak)合并它们.他指出,沃尔特曾要求他写一篇演…...
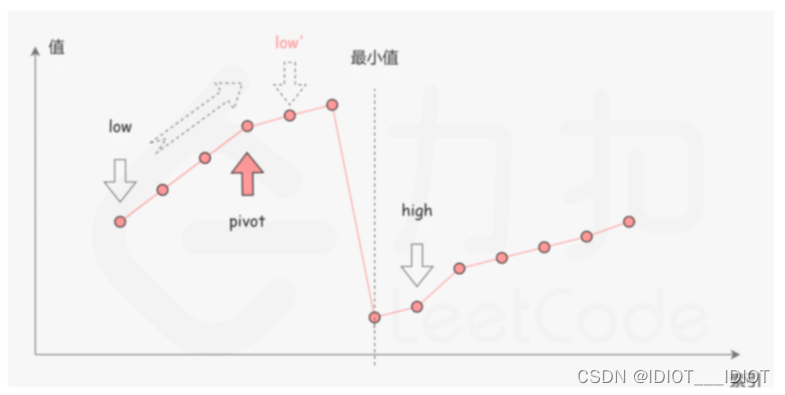
《算法通关村——二分查找在旋转数字中的应用》
《算法通关村——二分查找在旋转数字中的应用》 这里我们直接通过一个题目,来了解二分查找的应用。 153. 寻找旋转排序数组中的最小值 已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如&a…...
)
C/S架构学习之基于TCP的本地通信(服务器)
基于TCP的本地通信(服务器):创建流程:一、创建字节流式套接字(socket函数): int sock_fd socket(AF_LOCAL,SOCK_STREAM,0);二、创建服务器和客户机的本地网络信息结构体并填充服务器本地网络信…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...