智能优化算法(一):伪随机数的产生
文章目录
- 1.伪随机数介绍
- 1.1.伪随机产生的意义
- 1.2.伪随机产生的过程
- 2.产生U(0,1)的乘除同余法
- 2.1.原始的乘同余法
- 2.2.改进的乘同余法
- 3.产生正态分布的伪随机数
- 4.基于逆变法产生伪随机数
1.伪随机数介绍
1.1.伪随机产生的意义
1.随机数的产生是进行随机优化的第一步也是最重要的一步,随机优化算法运行过程中需要大量随机数。
2.传统手工方法:抽签,掷骰子,抽牌,摇号等,无法满足产生大量随机数的需求。
3.伪随机数方法:利用计算机通过某些数学公式计算而产生,从数学意义上说不是随机的,但只要通过随机数的一系列统计检验,就可以作为随机数来使用。
1.2.伪随机产生的过程
∙ \bullet ∙Step1:确定一个数学模型或某种规则。
∙ \bullet ∙Step2:规定几个初始值。
∙ \bullet ∙Step3:按照上述模型产生第一个随机数。
∙ \bullet ∙Step4:用产生的上一个随机数作为新的初值,按照相同的步骤产生下一个随机数,重复之,得到一个伪随机数序列。
2.产生U(0,1)的乘除同余法
2.1.原始的乘同余法
均匀的随机数的产生是生成其他随机数的基础,U(0,1)型随机数的产生主要是通过乘同余法进行设计生成,乘同余法的计算公式如下所示:
S k + 1 = ( A ⋅ S k ) m o d ( M ) S_{k+1}=(A\cdot S_k)\mathrm{~mod~}(M) Sk+1=(A⋅Sk) mod (M)
在公式中A表示整数常数, mod表示取模运算, M表示较大的整数
通过数论理论能够证明:
当 M = 2 L ( L > 2 ) M=2^{L}(L>2) M=2L(L>2)时,若 A = 4 k + 1 或者 A = 8 k + 3 A=4k+1或者A=8k+3 A=4k+1或者A=8k+3,且 S 0 S_{0} S0为奇数时,可以获得的最长随机数序列长度为 2 L − 2 2^{L-2} 2L−2.
算法实现如下所示:
%% 伪随机数的生成1--乘同余法
%乘同余法
%设定参数
clc;
S0=1;
A=3;
L=4;
M=2^L;
s=S0;
% 循环计算
fprintf('参数A=%d,M=%d,s0=%d的乘除同余法计算结果如下:\n',A,M,S0)
%得到的随机数循环周期为2^(L=2)个
for i =1:2^(L-2)s=mod(A*s,M);fprintf('第%d个随机数为:%d\n', i,s);
end
%如果想产生U(0,1)则需要将求出的s/M即可。
2.2.改进的乘同余法
对于普通的乘同余法只能获得周期为 2 L − 2 2^{L-2} 2L−2的随机数序列,这是远远不够的,所以我们通过添加一个与M互为质数的C来使得乘同余法获得周期为 2 L 2^{L} 2L的随机数数列,这种方法就被称作混合同余法,计算公式如下所示:
S k + 1 = ( A ⋅ S k + C ) m o d ( M ) S_{k+1}=(A\cdot S_k+C)\mathrm{~mod~}(M) Sk+1=(A⋅Sk+C) mod (M)
算法实现如下所示:
%% 伪随机数的生成2--混合乘同余法
%混合乘同余法
%设定参数
clc;
S0=1;
A=3;
L=4;
M=2^L;
s=S0;
C=3;
% 循环计算
fprintf('参数A=%d,M=%d,C=%d,S0=%d的乘除同余法计算结果如下:\n',A,M,C,S0)
%得到的随机数循环周期为2^(L)个
for i =1:2^(L)s=mod(A*s+C,M);fprintf('第%d个随机数为:%d\n', i,s);
end
%如果想产生U(0,1)则需要将求出的s/M即可。
3.产生正态分布的伪随机数
产生正态分布的伪随机数的基本原理:若 Y 1 , Y 2 , Y 3 . . . . . . Y n Y_{1},Y_{2},Y_{3}......Y_{n} Y1,Y2,Y3......Yn 是独立同分布,均值和方差分别为 μ \mu μ和 σ \sigma σ ,且 n n n较大,则 X = Y 1 + Y 2 + Y 3 . . . . . . + Y n X=Y_{1}+Y_{2}+Y_{3}......+Y_{n} X=Y1+Y2+Y3......+Yn 近似于正态分布,且满足 μ x = μ 1 + μ 2 + μ 3 . . . . . + μ n = n μ \mu_{x}=\mu_{1}+\mu_{2}+\mu_{3}.....+\mu_{n}=n\mu μx=μ1+μ2+μ3.....+μn=nμ 及 σ x 2 = σ 1 2 + σ 2 2 + σ 3 2 . . . . . + σ n 2 = n σ 2 \sigma_{x}^{2}=\sigma_{1}^{2}+\sigma_{2}^{2}+\sigma_{3}^{2}.....+\sigma_{n}^{2}=n\sigma_{}^{2} σx2=σ12+σ22+σ32.....+σn2=nσ2,即 x ∈ N ( n μ , n σ 2 ) x\in N( n \mu,n\sigma^{2}) x∈N(nμ,nσ2).
于是正态分布可以由多个U(0,1)来近似。
对于 Y ∈ U ( 0 , 1 ) Y\in U( 0,1) Y∈U(0,1) 来说,对于Y的均值有:
μ y = 1 2 \mu_y=\frac12 μy=21
对于Y的方差,计算如下所示:
σ y 2 = E ( Y 2 ) − ( E ( Y ) ) 2 = ∫ − ∞ + ∞ f ( y ) d y − ( 1 2 ) 2 = ∫ 0 1 y 2 d y − 1 4 = y 3 3 ∣ 1 0 − 1 4 = 1 12 \begin{aligned}\sigma_y^2&=E\color{r}{\left(Y^2\right)-\left(E(Y)\right)^2=\int_{-\infty}^{+\infty}f(y)dy-\left(\frac12\right)^2\\}=\int_0^1y^2dy-\frac14=\frac{y^3}3|\frac10-\frac14=\frac1{12}\end{aligned} σy2=E(Y2)−(E(Y))2=∫−∞+∞f(y)dy−(21)2=∫01y2dy−41=3y3∣01−41=121
令 z = x − μ x σ x z=\frac{x-\mu_x}{\sigma_x} z=σxx−μx,则 z ∈ N ( 0 , 1 ) z\in N(0,1) z∈N(0,1),则z的公式如下所所示:
z = ∑ y i − μ x σ x = ∑ y i − n μ y n σ y 2 = ∑ y i − n 2 n / 12 z=\frac{\sum y_i-\mu_x}{\sigma_x}=\frac{\sum y_i-n\mu_y}{\sqrt{n\sigma_y^2}}=\frac{\sum y_i-\frac n2}{\sqrt{n/_{12}}} z=σx∑yi−μx=nσy2∑yi−nμy=n/12∑yi−2n
一般取n=12,则z的计算公式为:
z = ∑ i = 1 12 y i − 6 ∈ N ( 0 , 1 ) z=\sum_{i=1}^{12}y_i-6\in N(0,1) z=i=1∑12yi−6∈N(0,1)
若想产生服从一般正态分布 N ( μ , σ 2 ) N(\mu,\sigma^{2}) N(μ,σ2) 的随机数x ,则只需产生 z ∈ N ( 0 , 1 ) z\in N(0,1) z∈N(0,1) ,再按公式 x = μ + σ z x=\mu+\sigma z x=μ+σz,即可获得 x ∈ N ( μ , σ 2 ) x\in N(\mu,\sigma^2) x∈N(μ,σ2).
算法实现如下所示(取 n = 1200 n=1200 n=1200计算结果好):
%% 伪随机数的生成3--正态分布方法
%正态分布方法
%设定参数
clc
%生成12个U(0,1)分布的随机数就直接调用包来解决
N=1200;
for i=1:1000Y=rand(N,1);z=(sum(Y)-N*0.5)/sqrt(N/12);fprintf('第%d个属于N(0,1)的随机数为:%.2f\n',i,z)
end
4.基于逆变法产生伪随机数
逆变法产生伪随机数的基本原理是设Y是(0,1)上均匀分布随机变量,F为任意一个连续分布函数,定义随机变量 X = F − 1 ( Y ) X=F^{-1}(Y) X=F−1(Y),则 X具有分布函数F。
证明如下:
F X ( a ) = P { X ≤ a } = P { F − 1 ( Y ) ≤ a } = P { Y ≤ F ( a ) } \begin{aligned}F_X(a)&=P\{X\leq a\}=P\{F^{-1}~(Y)\leq a\}=P\{Y\leq F(a)\}\end{aligned} FX(a)=P{X≤a}=P{F−1 (Y)≤a}=P{Y≤F(a)}
这里 Y ∈ U ( 0 , 1 ) Y\in U( 0,1) Y∈U(0,1) ,有
f ( y ) = 1 , F ( y ) = P { Y ≤ y } = ∫ − ∞ y f ( y ) d y = y f(y)=1,\quad F(y)=P\{Y\leq y\}=\int_{-\infty}^yf(y)dy=y f(y)=1,F(y)=P{Y≤y}=∫−∞yf(y)dy=y
最后能够推出:
F X ( a ) = F ( a ) F_X(a)=F(a) FX(a)=F(a)

相关文章:

智能优化算法(一):伪随机数的产生
文章目录 1.伪随机数介绍1.1.伪随机产生的意义1.2.伪随机产生的过程 2.产生U(0,1)的乘除同余法2.1.原始的乘同余法2.2.改进的乘同余法 3.产生正态分布的伪随机数4.基于逆变法产生伪随机数 1.伪随机数介绍 1.1.伪随机产生的意义 1.随机数的产生是进行随机优化的第一步也是最重要…...

python 调用Oracle有返回参数的存储过程
python 调用Oracle有返回参数的存储过程 1. 存储过程 create or replace procedure pro_test_args(a in integer,b in integer, c out integer) is beginc: a * b ;end pro_test_args;2. Python调用存储过程 import cx_Oracle import os import sys# 连接数据库 #conn cx_O…...

700. 二叉搜索树中的搜索
原题链接700. 二叉搜索树中的搜索 思路: 给定的就是一个二叉搜索树 二叉搜索树是一个有序树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结…...

GO学习之 互斥锁、读写锁该如何取舍
GO系列 1、GO学习之Hello World 2、GO学习之入门语法 3、GO学习之切片操作 4、GO学习之 Map 操作 5、GO学习之 结构体 操作 6、GO学习之 通道(Channel) 7、GO学习之 多线程(goroutine) 8、GO学习之 函数(Function) 9、GO学习之 接口(Interface) 10、GO学习之 网络通信(Net/Htt…...

Internet的特点
Internet是一个全球性的计算机网络系统,它将全世界各个地方已有的各种网络(如计算机网、数据通信网以及公用电话交换网等)互联起来,组成一个跨越国界范围的庞大的互联网,因此,也称为“网络的网络”。Internet在很短的时间内风靡全…...

Rust4.2 Common Collections
Rust学习笔记 Rust编程语言入门教程课程笔记 参考教材: The Rust Programming Language (by Steve Klabnik and Carol Nichols, with contributions from the Rust Community) Lecture 8: Common Collections fn main() {//Vectorlet mut v: Vec<i32> Vec::new();//…...

芸鹰蓬飞:抖音投流以后还有自然流量吗?
随着抖音平台的普及,企业和个人纷纷加入到这个短视频的热潮中。然而,一旦投入抖音投流,是否还能依赖自然流量?这是许多用户和品牌关心的问题。本文将深入剖析这一话题,探讨抖音投流与自然流量之间的关系。 一、抖音投…...
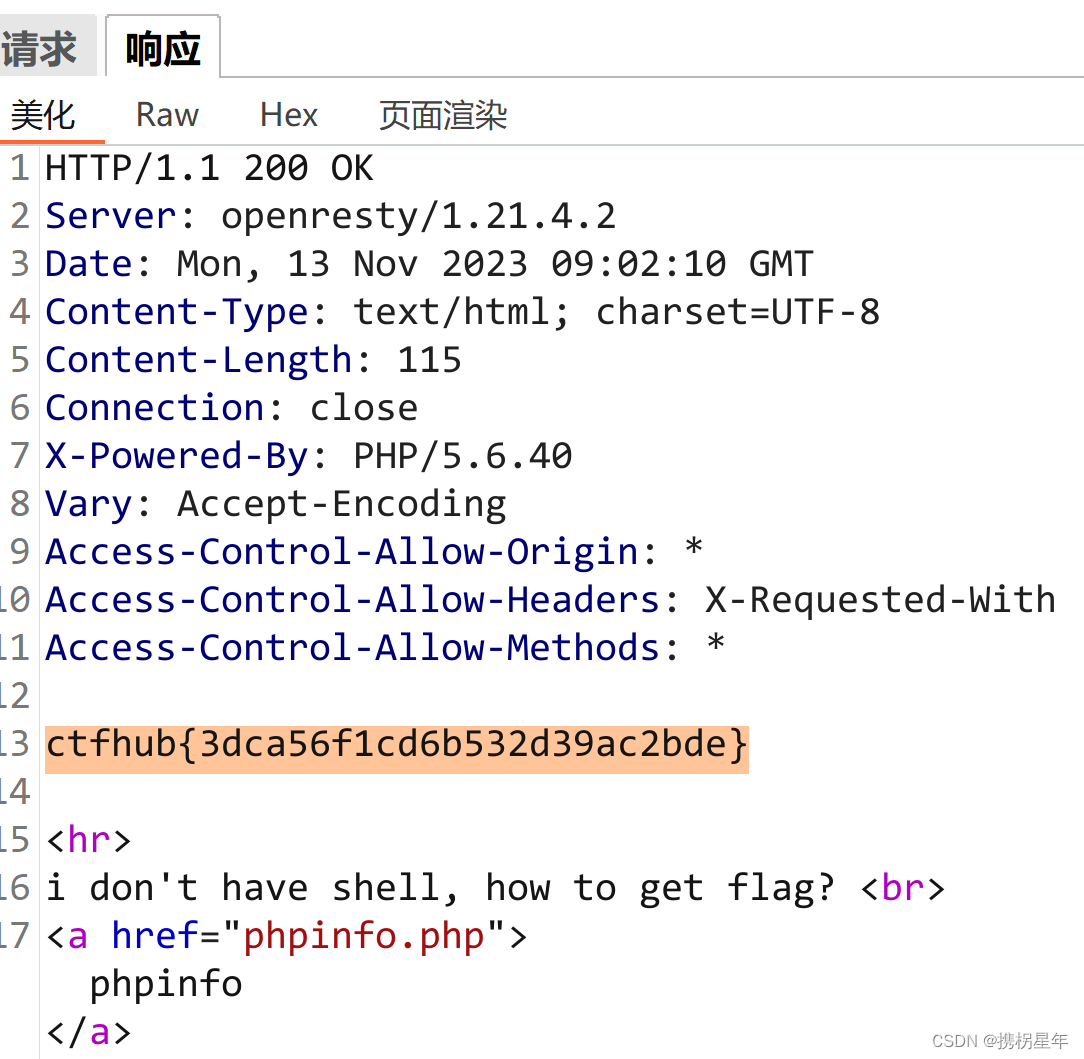
CTFhub-RCE-php://input
我们需要使用php://input来构造发送的指令 查看phpinfo,找到一下字段 证明是可以使用php://input 1. 使用Burpsuite抓包并转至Repeater 2. 构造包 方法:POST 目标:/?filephp://input Body:<?php system("ls /"…...

RISC-V处理器设计(五)—— 在 RISC-V 处理器上运行 C 程序
目录 一、前言 二、从 C 程序到机器指令 三、实验 3.1 实验环境 3.11 Windows 平台下环境搭建 3.12 Ubuntu 平台下环境搭建 3.13 实验涉及到的代码或目录 3.2 各文件作用介绍 3.2.1 link.lds 3.2.2 start.S 3.2.3 lib 和 include 目录 3.2.4 common.mk 3.2.5 demo …...
【PIE-Engine 数据资源】全球250米LAI产品
文章目录 一、 简介二、描述三、波段四、示例代码参考资料 一、 简介 数据名称全球250米LAI产品时间范围2015年空间范围全球数据来源北京师范大学肖志强教授团队代码片段var images pie.ImageCollection(“BNU/LAI/GLOBAL-250”) 二、描述 全球 250 米叶面指数产品由北京师范…...

vcomp120.dll丢失怎么办?vcomp120.dll丢失的解决方法分享
vcomp120.dll丢失”。这个错误通常会导致某些应用程序无法正常运行,给用户带来困扰。那么,当我们遇到这个问题时,应该如何修复呢?下面我将为大家介绍四个修复vcomp120.dll丢失的方法。 一、使用dll修复程序修复 可以通过百度或许…...

linux下使用Docker Compose部署Spug实现公网远程访问
📑前言 本文主要是linux下使用Docker Compose部署Spug实现公网远程访问的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是青衿🥇 ☁️博客首页:CSDN主页放风讲故事 &am…...
【STM32 CAN】STM32G47x 单片机FDCAN作为普通CAN外设使用教程
STM32G47x 单片机FDCAN作为普通CAN外设使用教程 控制器局域网总线(CAN,Controller Area Network)是一种用于实时应用的串行通讯协议总线,它可以使用双绞线来传输信号,是世界上应用最广泛的现场总线之一。CAN协议用于汽…...

Apache Log4j2漏洞
Log4j2是一个Java日志组件,被各类Java框架广泛地使用。它的前身是Log4j,Log4j2重新构建和设计了框架,可以认为两者是完全独立的两个日志组件。本次漏洞影响范围为Log4j2最早期的版本2.0-beta9到2.15.0。Log4j2分为2个jar包,一个是接口log4j-api-${版本号}.jar,一个是具体实…...
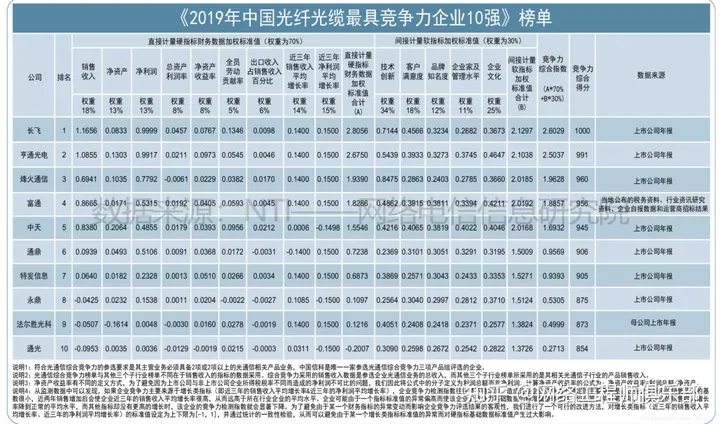
超级干货:光纤知识总结最全的文章
你们好,我的网工朋友。 光纤已经是远距离有线信号传输的主要手段,而安装、维护光纤也是很多人网络布线的基本功。 在网络布线中,通常室外楼宇间幢与幢之间使用的是光缆,室内楼宇内部大都使用的是以太网双绞线,也有使用…...
PyCharm因安装了illuminated Cloud插件导致加载项目失败
打开Pycharm时会有弹窗提示: The license for Illuminated Cloud is invalid or has expired. All Illuminated Cloud features will be disabled. 这个弹窗会导致你加载项目一直失败,close project 也关不掉,我都是用任务管理器杀死进程的…...

微服务拆分的一些基本原则
文章首发公众号:海天二路搬砖工 单一职责原则 什么是单一职责原则 单一职责原则原本是面向对象设计中的一个基本原则,它指的是一个类只负责一项职责,不要存在多于一个导致类变更的原因。 在微服务架构中,一个微服务也应该只负…...
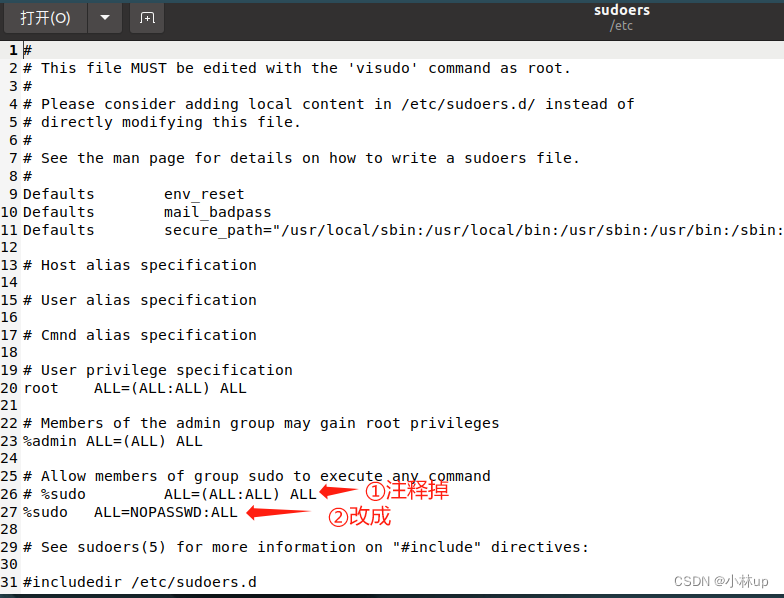
Ubuntu取消sudo的输入密码
Ubuntu最近要安装软件,每次sudo都要输入一次密码,感觉很麻烦,于是想能不能设置为不输入密码,在网上找了一下解决办法。 主要参考这篇文章: Ubuntu取消sudo时输入密码 上面这篇文章使用的是vim,但是按照博…...

基于ubuntu22.04手动安装openstack——2023.2版本(最新版)的问题汇总
前言:基本上按照openstack官方网站动手可以搭建成功(如有需要私信发部署文档)。 但是任然有些小问题,所以汇总如下。 第一个问题 问题: ubuntu搭建2023.2版本neutorn报错,ERROR neutron.plugins.ml2.driv…...

如何入门学习黑客技术?如何选择编程语言?如何选择适合黑客的操作系统?
‘ 一 ’ 了解黑客技术的基础知识 学习黑客技术需要对网络安全和计算机系统有一定的了解。可以通过参加安全培训班、阅读专业书籍和学术论文、浏览网络安全博客和论坛等方式获取基础知识。涉及的内容包括网络协议、操作系统原理、计算机网络和编程等。 ‘ 二 ’ 选择适合你的…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
