【LeetCode】67. 二进制求和
67. 二进制求和
难度:简单
题目
给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。
示例 1:
输入:a = "11", b = "1"
输出:"100"
示例 2:
输入:a = "1010", b = "1011"
输出:"10101"
提示:
1 <= a.length, b.length <= 10^4a和b仅由字符'0'或'1'组成- 字符串如果不是
"0",就不含前导零
个人题解
思路:
- 从后往前遍历字符逐个判断即可
- 最后考虑是否进位
- sum & 1 等价于 sum % 2
class Solution {public String addBinary(String a, String b) {StringBuilder ans = new StringBuilder();int ca = 0;for (int i = a.length() - 1, j = b.length() - 1; i >= 0 || j >= 0; i--, j--) {int sum = ca;sum += i>= 0 ? a.charAt(i) - '0' : 0;sum += j>= 0 ? b.charAt(j) - '0' : 0;ca = sum / 2;ans.append(sum & 1);}if (ca == 1) {ans.append(1);}return ans.reverse().toString();}
}
相关文章:

【LeetCode】67. 二进制求和
67. 二进制求和 难度:简单 题目 给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。 示例 1: 输入:a "11", b "1" 输出:"100"示例 2: 输入:a "…...

【LeetCode刷题笔记】二叉树(一)
102. 二叉树的层序遍历 解题思路: 1. BFS广度优先遍历 ,使用队列,按层访问 解题思路: 2. 前序遍历 , 递归 ,在递归方法参数中,将 层索引...

NativeScript开发ios应用,怎么生成测试程序?
在 NativeScript 中,要部署 iOS 应用程序,你需要遵循以下一般步骤: 1、确保开发环境: 确保你的开发环境中已经安装了 Xcode,并且你有一个有效的 Apple 开发者账号。 2、构建 iOS 应用: 在你的 NativeScri…...

Js面试题:说一下js的模块化?
作用: 一个模块就是实现某个特定功能的文件,在文件中定义的变量、函数、类都是私有的,对其他文件不可见。 为了解决引入多个js文件时,出现 命名冲突、污染作用域 等问题 AMD: 浏览器端模块解决方案 AMD即是“异步模块定…...
媒体转码软件Media Encoder 2024 mac中文版功能介绍
Media Encoder 2024 mac是一款媒体转码软件,它可以将视频从一种格式转码为另一种格式,支持H.265、HDR10等多种编码格式,同时优化了视频质量,提高了编码速度。此外,Media Encoder 2024还支持收录、创建代理和输出各种格…...

整治PPOCRLabel中cv2文件读取问题(更新中)
PPOCRLabel 使用PPOCRLabel对ocr预标注结果进行纠正由于PaddleOCR代码库十分混乱,路径经常乱调pip和代码库的代码(pip库和源码冲突),经常报错,因此paddleocr和ppocrlabel都是使用pip包;PPOCRLabel中使用了cv2进行图片数据的读取,…...

网络运维Day09-补充
文章目录 rsync增量同步scp与rsync的区别rsync常用选项 rsync本地实验rsync远程同步实验练习上传练习下载 总结 rsync增量同步 rsync是增量同步的一种工具,可以实现本地目录之间数据同步,也可以实现远程跨主机之间数据同步 scp与rsync的区别 scp属于全…...
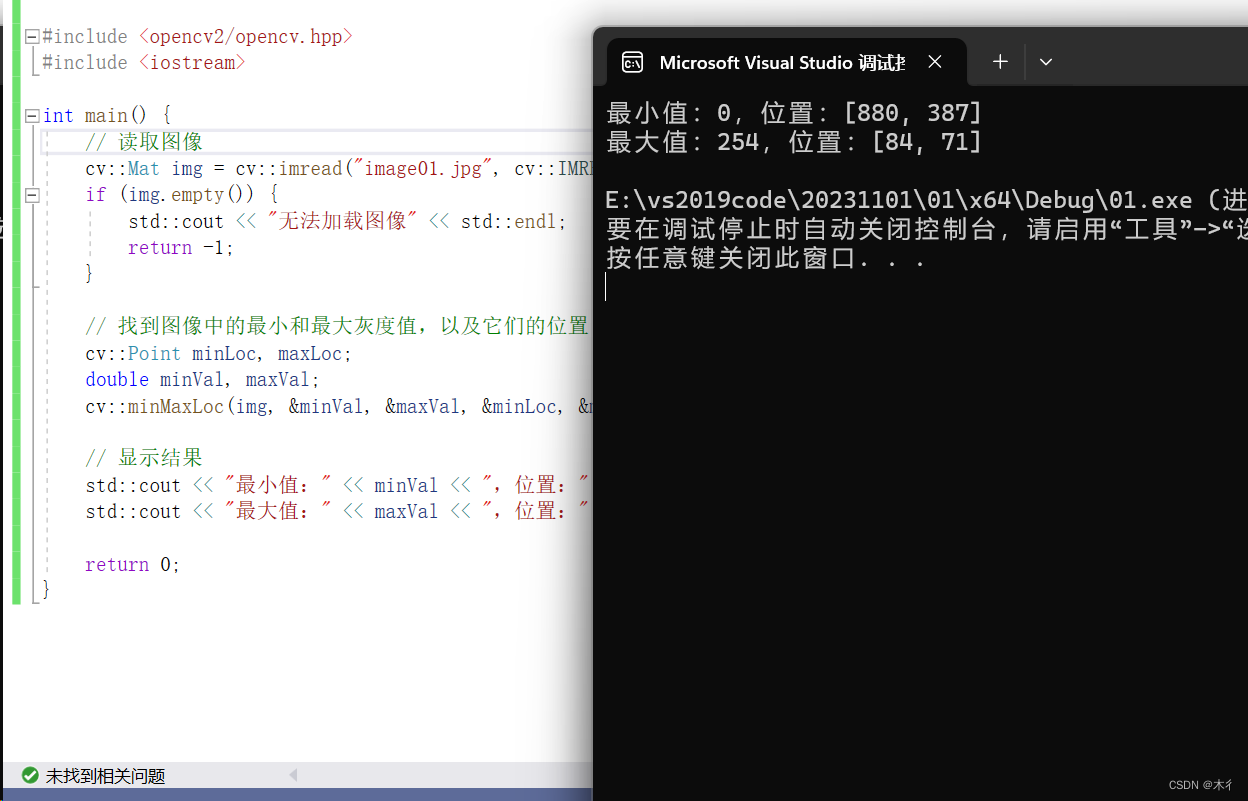
【C++】【Opencv】minMaxLoc()函数详解和示例
minMaxLoc()函数 是 OpenCV 库中的一个函数,用于找到一个多维数组中的最小值和最大值,以及它们的位置。这个函数对于处理图像和数组非常有用。本文通过参数和示例详解,帮助大家理解和使用该函数。 参数详解 函数原型…...
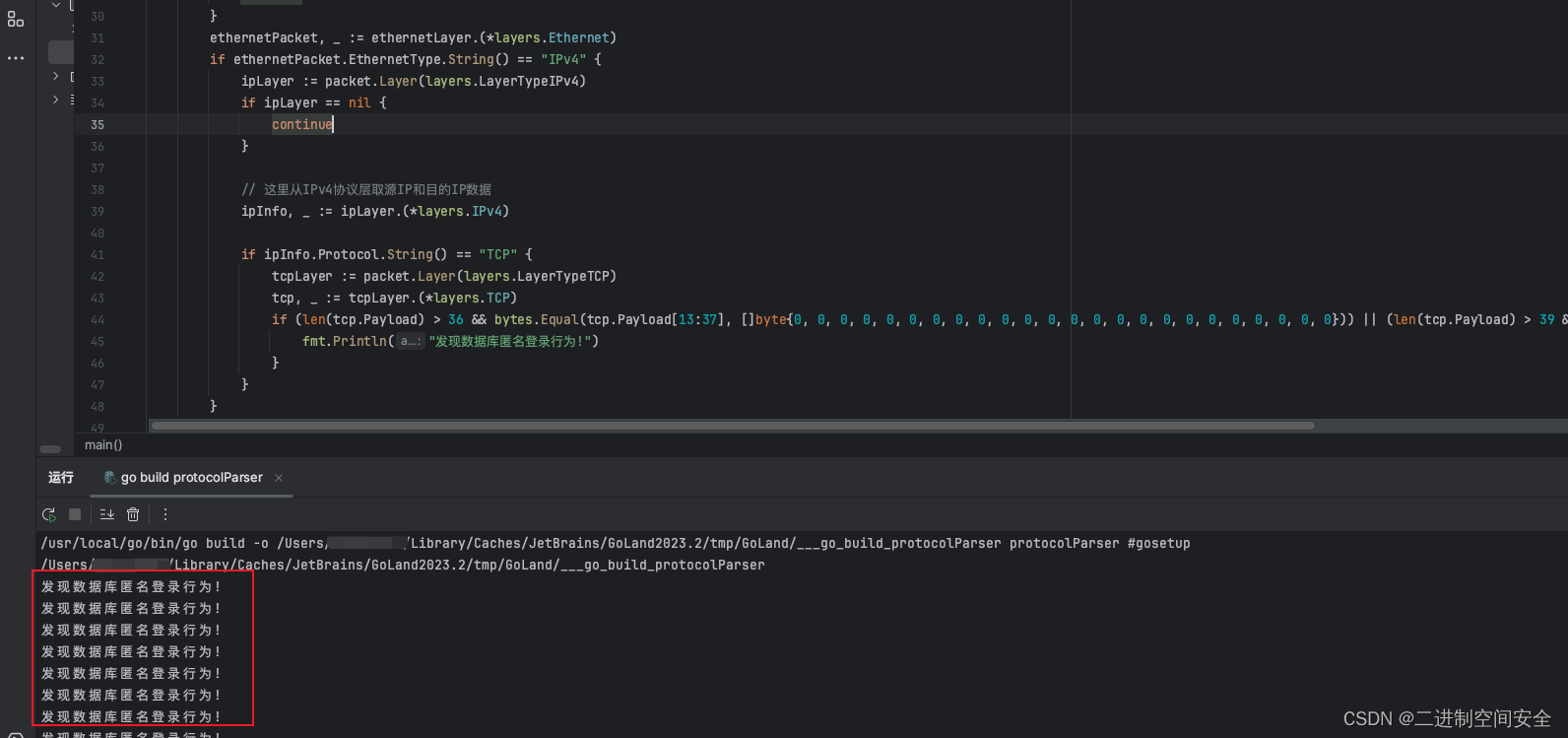
用Go实现网络流量解析和行为检测引擎
1.前言 最近有个在学校读书的迷弟问我:大德德, 有没有这么一款软件, 能够批量读取多个抓包文件,并把我想要的数据呈现出来, 比如:源IP、目的IP、源mac地址、目的mac地址等等。我说:“这样的软件你要认真找真能找出不少开源软件, 但毕竟没有你自己的灵魂在里面,要不…...

Mysql数据备份 — mysqldump
一 备份类型 - 逻辑备份(mysqldump): - 优点: - 恢复简单,可以使用管道将他们输入到mysql。 - 与存储引擎无关,因为是从MySQL服务器中提取数据而生成的,所以消除了底层数据…...

vue使用Echarts5实现词云图
先上官网 词云图有些特殊,它属于Echarts 的扩展,需要额外安装Echarts-wordcloud包。 Echarts 官网 Echarts-wordcloud 词云图官网 先安装 npm install echarts npm install echarts-wordcloud再引入 echarts选一个引入就行;4或5版本都可以 …...
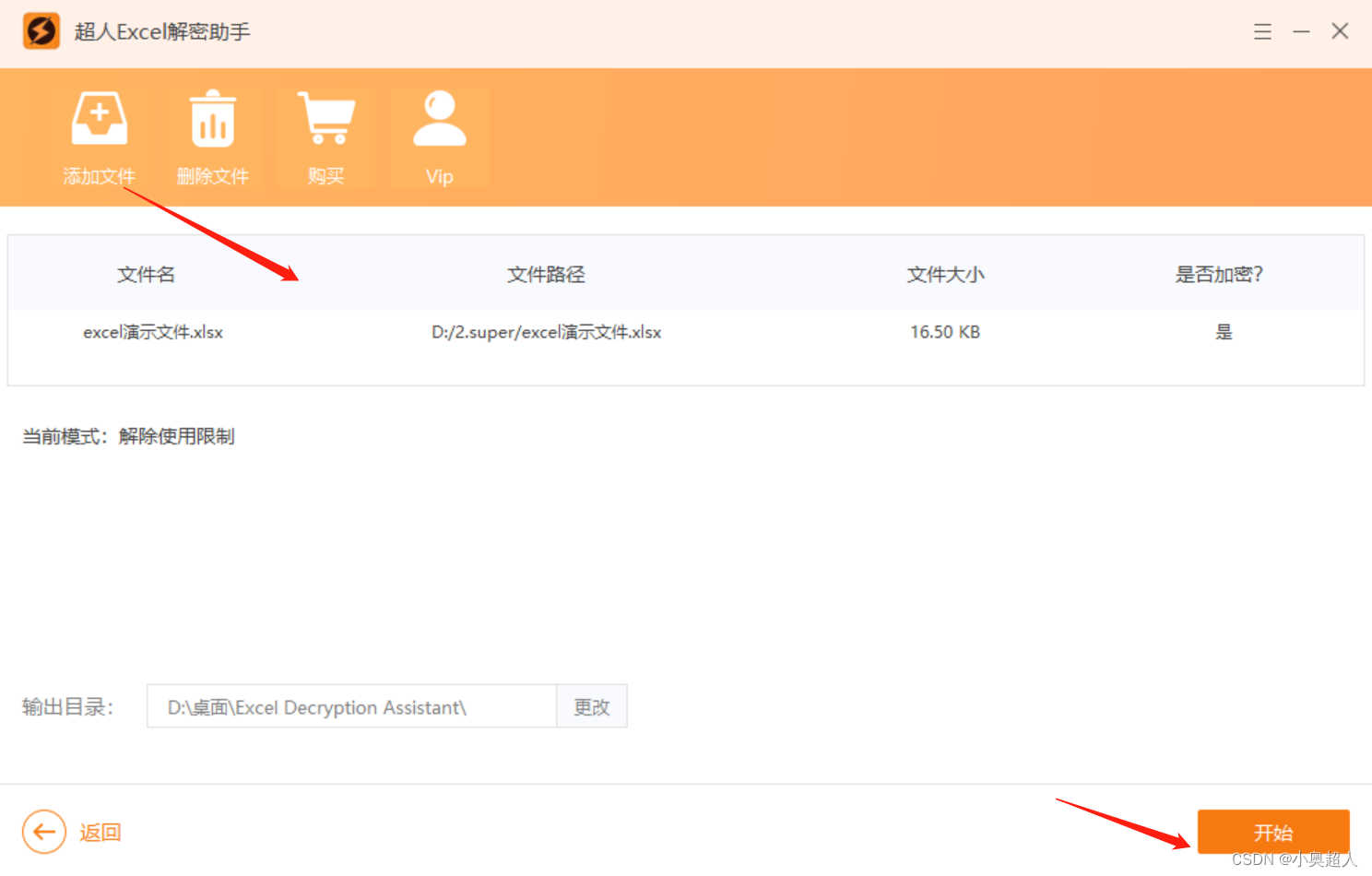
带有密码的Excel只读模式,如何取消?
Excel文件打开之后发现是只读模式,想要退出只读模式,但是只读模式是带有密码的,该如何取消带有密码的excel只读文件呢? 带有密码的只读模式,是设置了excel文件的修改权限,取消修改权限,我们需要…...

Linux下基本操作命令
一、基础命令 1. pwd 命令 pwd命令用于显示当前所在的工作目录的全路径名称。该命令无需任何参数,只需在终端窗口中输入 pwd 命令即可使用。 2. cd 命令 cd命令用于更改当前工作目录。该命令需要一个参数:目标目录名称。例如,若要进入 Do…...

JVS低代码表单自定义按钮的使用说明和操作示例
在普通的表单设计中,虽然自带的【提交】、【重置】、【取消】按钮可以满足基本操作需求,但在面对更多复杂的业务场景时,这些按钮的显示控制就显得有些力不从心。为了更好地满足用户在表单操作过程中的个性化需求,JVS低代码推出了表…...
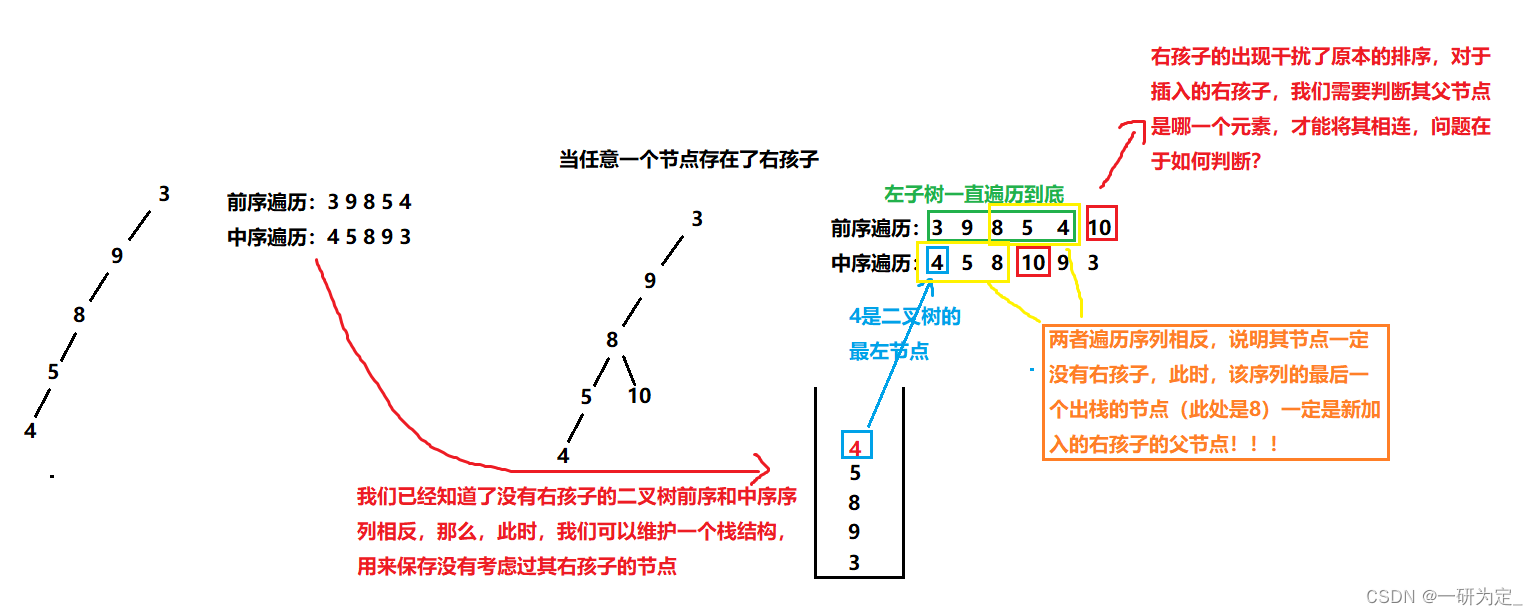
C++--二叉树经典例题
本文,我们主要讲解一些适合用C的数据结构来求解的二叉树问题,其中涉及了二叉树的遍历,栈和队列等数据结构,递归与回溯等知识,希望可以帮助你进一步理解二叉树。 目录 1.二叉树的层序遍历 2.二叉树的公…...

软件测试需要学习什么?好学吗?需要学多久?到底是报班好还是自学好?
前言: 我发现很多的小伙伴刚刚毕业和想转行的小伙伴对于软件测试很陌生,其中很有很多的小伙伴还踩不少的坑,花费了大量的精力和时间去探索,结果还是一无所获。这里给大家出一期关于软件测试萌新的疑惑,看完这篇文章你就…...

Ubuntu搭建AI画图工具stable diffusion-webui
Ubuntu搭建 安装依赖项 安装以下依赖项: # Debian-based: sudo apt install wget git python3 python3-venv libgl1 libglib2.0-0# Red Hat-based: sudo dnf install wget git python3# Arch-based: sudo pacman -S wget git python3下载并安装WebUI 进入您想要安…...

智能优化算法(一):伪随机数的产生
文章目录 1.伪随机数介绍1.1.伪随机产生的意义1.2.伪随机产生的过程 2.产生U(0,1)的乘除同余法2.1.原始的乘同余法2.2.改进的乘同余法 3.产生正态分布的伪随机数4.基于逆变法产生伪随机数 1.伪随机数介绍 1.1.伪随机产生的意义 1.随机数的产生是进行随机优化的第一步也是最重要…...

python 调用Oracle有返回参数的存储过程
python 调用Oracle有返回参数的存储过程 1. 存储过程 create or replace procedure pro_test_args(a in integer,b in integer, c out integer) is beginc: a * b ;end pro_test_args;2. Python调用存储过程 import cx_Oracle import os import sys# 连接数据库 #conn cx_O…...

700. 二叉搜索树中的搜索
原题链接700. 二叉搜索树中的搜索 思路: 给定的就是一个二叉搜索树 二叉搜索树是一个有序树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
