博弈论入门
目录
什么是博弈?
博弈论的发展历史?
博弈的要素有哪些?
博弈的分类?
博弈论的应用
收益矩阵
纳什均衡的定义
博弈论的例子
1、田忌赛马
2、穷途困境
2.1优化反应函数法
2.2Nashpy库
2.3顶点枚举算法
3、Nash游戏
4、巴什博奕(Bash Game)
5、威佐夫博弈(Whthoff Game)
6、电子商务中的定价策略
什么是博弈?
概念1:博弈是指在一定的游戏规则约束下,基于直接相互作用的环境条件,各参与人依靠所掌握的信息,选择各自策略(行动),以实现利益最大化和风险成本最小化的过程。简单说就是人与人之间为了谋取利益而竞争。
概念2:博弈是指在平等的对决中参与双方分别根据对方的策略指定自己的应对策略,从而取得胜利。
博弈论的发展历史?
博弈论的发展历史可以追溯到两千多年前的中国和古希腊,最早的博弈案例包括《孙子兵法》、《孙膑兵法》、《三十六计》、《六韬》等书籍中的故事。然而,博弈论真正成为一门系统的学科,是在20世纪初。
在20世纪20年代,法国数学家波莱尔首次用数学语言刻画了博弈问题,提出了“策略”和“混和策略”概念,并用最佳策略和概念研究了下棋等决策问题。同时,德国哲学家和数学家莱布尼茨在1710年就预言了关于策略博弈理论出现的必要性和可能性。
随后,在1928年,约翰·冯·诺依曼与奥斯卡·摩根斯坦合作出版了《博弈论与经济行为》,标志着博弈论的正式诞生。他们提出了两人零和博弈的极小极大定理,并证明了博弈论的基本定理。
在20世纪50年代,博弈论发展到了鼎盛时期,包括纳什、海萨尼和泽尔腾等人在内的众多学者做出了重要贡献。纳什提出了“纳什均衡”的概念,海萨尼和泽尔腾等人也在合作博弈领域做出了重要贡献。
自那时起,博弈论在经济学、政治学、生物学等多个领域得到了广泛应用。尤其是经济学领域,许多学者如纳什、海萨尼和泽尔腾等,在博弈论领域做出了重要贡献。1994年,纳什、海萨尼和泽尔腾因在博弈论领域的突出贡献获得了诺贝尔经济学奖。
博弈论在军事战略、国际关系、法律等领域也有着广泛的应用。它提供了一种方法来理解和预测在特定环境中的行为结果,帮助人们制定出最优策略。
博弈的要素有哪些?
参与者:至少有两个参与者,他们之间存在相互依赖的关系。
策略集:每个参与者都有一套完整的策略集,定义了在不同状态下他们可以选择的行动。
效用函数:衡量参与者在每一组策略组合下的收益,参与者总是愿意选择高收益而不是低收益。
信息:参与者根据他们所掌握的信息做出决策。
博弈的分类?
博弈可以根据不同的标准进行分类,以下是一些常见的分类方式:
按照参与人数分类:可以分为单人博弈、双人博弈、多人博弈。
按照策略数量分类:可以分为有限策略博弈和无限策略博弈。
按照参与人对其他参与人的了解程度分类:可以分为静态博弈和动态博弈。
按照其他因素分类:例如,按照博弈中的得益分类,可以分为零和博弈、常和博弈、变和博弈;按照参与人之间是否合作分类,可以分为合作博弈和非合作博弈等。
此外,根据博弈的研究范式和研究方法的不同,博弈论还可以分为传统博弈论和演化博弈论等。
博弈论的应用
博弈论在许多领域都有广泛的应用,如生物学、经济学、国际关系、计算机科学、政治学、军事战略等。在经济学中,博弈论已经成为标准分析工具之一,生物学家使用博弈理论来理解和预测进化论的某些结果。
此外,博弈论也可以被视为一种思维方式和决策方法。它帮助人们分析问题,找到最优策略,以及理解和预测他人的行为。在商业、政治和日常生活中,博弈论都有广泛的应用,如商业策略、国际关系分析、法律和政策制定等。

收益矩阵
有两名玩家A 和 B ,每个玩家都有两种策略,A 可以选择“TOP”或者“Bottom”,B 可以选择“Left”或者“Right”。做出不同的行为所对应的收益也是不同的。将二者的收益整理成如下矩阵,A的策略在左边,红色表示A的收益;B的策略在上边,蓝色表示B的收益。
纳什均衡的定义
在博弈论中,纳什均衡是指在博弈中所有参与者都采取最优策略的状态。具体来说,如果在一个博弈中,每参与者都选择了一种策略,且没有任何一个参与者可以通过改变自己的策略来获得更好的结果,那么这个状态就是一个纳什均衡。
纳什均衡可以分成两类:“纯策略纳什均衡”和“混合策略纳什均衡”。
纯策略(pure strategies)指的是如果一个策略规定参与人在每一个给定的信息情况下只选择一种特定的行动,称为纯策略,简称“策略” ,即参与人在其策略空间中选取唯一确定的策略。纯策略纳什均衡指的是,参与人采用纯策略确定的均衡。
混合策略(mixed strategies)指的是如果一个策略规定参与人在给定的信息情况下以某种概率分布随机地选择不同的行动,称为混合策略。参与人采取的不是明确唯一的策略,而是其策略空间上的一种概率分布。混合策略纳什均衡指的是,参与人采用混合策略确定的均衡。

博弈论的例子
1、田忌赛马
齐国大将田忌很喜欢赛马。他和齐威王约定,进行一次赛马比赛。他们各自将自己的马分为上、中、下三等,依次派出上等马、中等马和下等马,进行三轮比赛。由于齐威王每个等级的马都比田忌强,三场比赛下来,田忌都失败了。田忌军师孙膑帮他想了一个对策,建议田忌调整赛马顺序,先用下等马对齐威王的上等马,再拿上等马对齐威王的中等马,最后拿中等马对齐威王的下等马,三局两胜,以弱胜强,反败为胜!
以下为单次对决的代码:
import nashpy as nash
import numpy as np
'''
假设田忌有3匹马(A、B、C),
齐王有4匹马(a、b、c)
Aa上等马
Bb中等马
Cc下等马
'''
tianji_strategies = ["A", "B", "C"]
qiwang_strategies = ["a", "b", "c"]
tianji_payoff = np.array([[-1, 1, 2],[-2, -1, 1],[-3, -2, -1]])
qiwang_payoff = np.array([[1, -1, -2],[2, 1, -1],[3, 2, 1]])
game = nash.Game(tianji_payoff, qiwang_payoff)
equilibria = game.support_enumeration()
for eq in equilibria:print("纳什均衡策略组合:", eq)
# #重复博弈
# for _ in range(3):
# game = nash.Game(tianji_payoff, qiwang_payoff)
# equilibria = game.support_enumeration()
# tianji_payoff, qiwang_payoff = qiwang_payoff, tianji_payoff # 交换角色
# print(list(equilibria))纳什均衡策略组合:(array([1., 0., 0.]), array([1., 0., 0.]))
2、穷途困境
两个人因盗窃被捕,警方怀疑其有抢劫行为,但未获得确凿证据可以判他们犯了抢劫罪,除非有一个人供认或两个人都供认。即使两个人都不供认,也可判他们犯盗窃物品的轻罪。犯罪嫌疑人被分离审查,不允许他们之间互通消息,并交代政策如下:如果两个人都供认,每个人都将因抢劫罪加盗窃罪被判2年监禁;如果两个人都拒供,则两个人都将因盗窃罪被判处半年监禁;如果一个人供认而另一个拒供,则供认者被认为有立功表现而免受处罚,拒供者将因抢劫罪,盗窃罪以及抗拒从严而被重判5年。
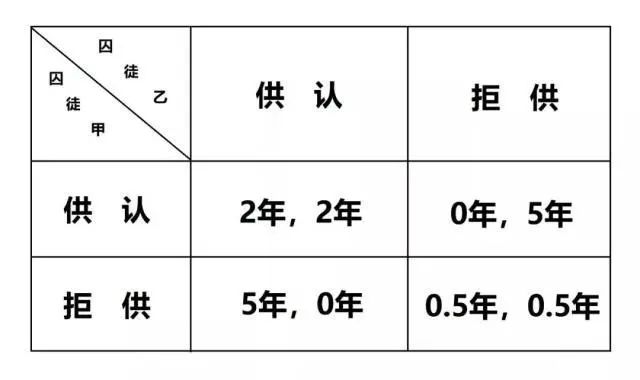
2.1优化反应函数法
import numpy as np
# 定义博弈矩阵
A = np.array([[[-2, -2], [0, -5]],[[-5, 0], [-0.5, -0.5]]
])
# 计算最优反应函数
def best_response(A,i):j = 1 - ireturn np.unravel_index(np.argmax(A[i, :, j]), A.shape[:2])[0]
# 计算纳什均衡
br1 = best_response(A, 0)
br2 = best_response(A, 1)
if A[br1, br2, 0] == A[br1, br2, 1]:print(f'({br1}, {br2}) is a Nash equilibrium')
else:print('No Nash equilibrium')(0, 0) is a Nash equilibrium
0-供认,1-拒供
甲乙都供认
2.2Nashpy库
纯策略
import numpy as np
import nashpy as nash
A = np.array([[-2, 0], [-5, -0.5]])
B = np.array([[-2, -5], [0, -0.5]])
game = nash.Game(A, B)
eqs = game.support_enumeration()
for eq in eqs:eq_left, eq_right = eqexpected_payoff_left = np.dot(eq_left, A).dot(eq_right)expected_payoff_right = np.dot(eq_left, B).dot(eq_right)print("左方策略:", eq_left, ",右方策略:", eq_right, ",左方期望效用值:", expected_payoff_left, ",右方期望效用值:", expected_payoff_right)左方策略:[1. 0.] ,右方策略:[1. 0.] ,左方期望效用值:-2.0 ,右方期望效用值:-2.0
0-供认,1-拒供
甲乙都供认,即刑期2年,
混合策略
import nashpy as ns
import numpy as np
A = np.array([[2, 0], [5, 0.5]])
B = np.array([[2, 5], [0, 0.5]])
payoff = ns.Game(A, B)
r = np.array([.5, .5]) # A玩家对应策略概率
c = np.array([0.7, 0.3]) # B玩家对应策略概率
payoff = ns.Game(A, B)
print(payoff[r, c])[-2.525 -1.525]
甲以0.5的概率选这供认,0.5的概率选择拒供,收益2.525年刑期
甲以0.7的概率选这供认,0.3的概率选择拒供,收益1.525年刑期
2.3顶点枚举算法
import numpy as np
# 两个玩家的收益矩阵
A = np.array([[2, 0], [5, 0.5]])
B = np.array([[2, 5], [0, 0.5]])
# 玩家策略空间
strats_A = [0, 1]
strats_B = [0, 1]
def vertex_enumeration(A, B, strats_A, strats_B):
equilibria = []
# 枚举所有顶点for s_A in strats_A:for s_B in strats_B:
# 计算最优响应br_A = np.argmax(A[s_B, :])br_B = np.argmax(B[:, s_A])
# 判断均衡if s_A == br_A and s_B == br_B:equilibria.append((s_A, s_B))
return equilibria
print(vertex_enumeration(A, B, strats_A, strats_B))[(0, 0)]
3、Nash游戏
裁判拿出n个棋子,n可能很多。你和对手轮流取子,规则是:
当n是奇数时,你和对手都只容许拿走1颗棋子,
n是偶数时,有两个选择:拿走一个,或拿走一半,由自己判断选择采取哪一种做法。取胜的条件是:拿走棋子数量最多的取胜或没有棋子拿的失败。
4、巴什博奕(Bash Game)
一堆n个物品,两个人轮流从中取出(1~m)个,轮到谁取时发现物品没有了,判定该玩家输。
def bash_game(n, m):# 判断当前轮到的玩家是否处于必胜状态if n % (m + 1) == 0:return "后手必胜"else:return "先手必胜"
# 输入物品数量n和每轮最多取出的数量m
n = int(input("请输入物品数量n:"))
m = int(input("请输入每轮最多取出的数量m:"))
# 调用函数并输出结果
result = bash_game(n, m)
print(result)
5、威佐夫博弈(Whthoff Game)
有两堆各若干个物品,两位玩家轮流从任意一堆中取出至少一个或者同时从两堆中取出同样多的物品,规定每次至少取一个,至多不限(两堆不一定一样多),轮到谁取时发现物品没有了,判定该玩家输。
6、电子商务中的定价策略
两家公司A和B在网上销售同一产品。公司A可以选择以10美元或20美元的价格出售其产品,而公司B可以选择以10美元或15美元的价格出售其产品。给出每家公司的最优定价策略?
参考文献1、https://nashpy.readthedocs.io/en/stable/text-book/index.html2、《哈林顿博弈论》,哈林顿,中国人民大学出版社3、《用博弈的思维看世界》,蒋文华,浙江大学出版社
相关文章:

博弈论入门
目录 什么是博弈? 博弈论的发展历史? 博弈的要素有哪些? 博弈的分类? 博弈论的应用 收益矩阵 纳什均衡的定义 博弈论的例子 1、田忌赛马 2、穷途困境 2.1优化反应函数法 2.2Nashpy库 2.3顶点枚举算法 3、Nash游戏 …...

php加密解密
public static function encrypt($data, $key) {$key 111;// 生成盐值$salt openssl_random_pseudo_bytes(16);// 使用盐值和密钥进行加密$encrypted openssl_encrypt($data, AES-128-CBC, $key, 0, $salt);// 将盐值和加密后的数据拼接$result base64_encode($salt . $enc…...

基于YOLOv8的输电线路异物识别算法应用
基于 YOLOv8 的输电线路异物识别算法应用 输电线路作为电力系统的重要一环,保证其安全稳定运行是十分必要的。由于长期暴露于室外,线路所面临的不安全因素繁多,异物入侵便是其中之一。异物可能会引起线路短路甚至诱发火灾,因此要加…...
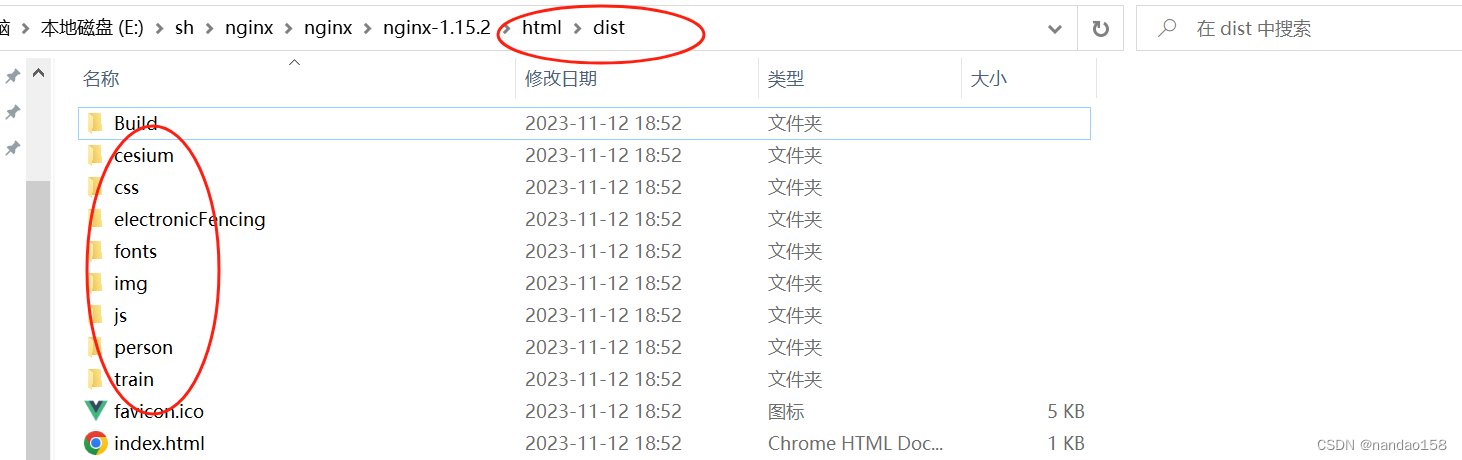
win环境Jenkins部署前端项目
今天分享win环境Jenkins部署前端vue项目,使用的版本jenkins版本Jenkins 2.406版本。 前提是jenkins安装好了,通用配置已经配置好了,可以参考上两篇博客。 1、前端项目依赖nodejs,需要安装相关插件 点击进入 安装成功标准 jenki…...

DDD领域驱动设计模式结构图面向接口编程
DDD领域驱动设计模式结构图面向接口编程 9.资源库 在刚接触资源库(Repository)时,第一反应便是这就是个 DAO 层,访问数据库,然后吧啦吧啦,但是,当接触的越久,越发认识到第一反应是错的,资源库更…...

Ubuntu中安装R语言环境并在jupyter kernel里面增加R kernel
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️ 👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
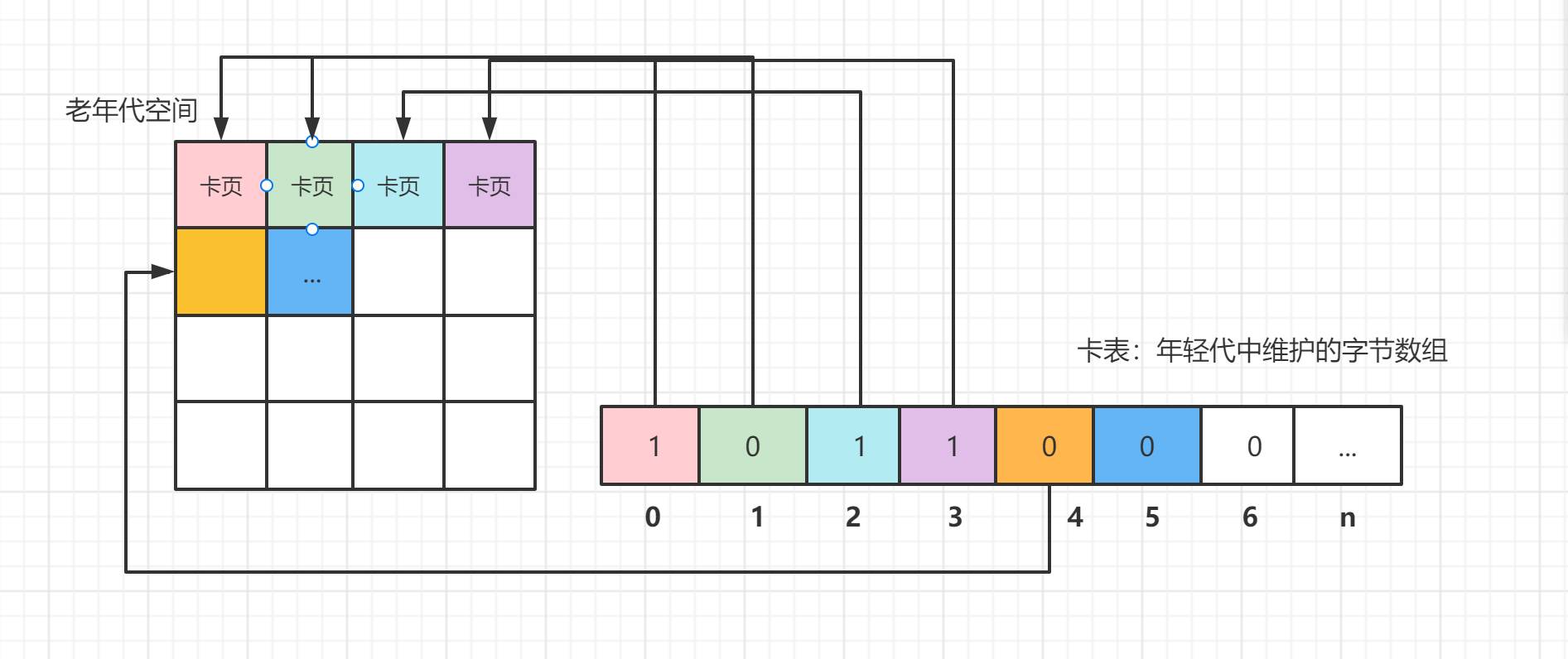
JVM:如果是你,你如何解决跨代引用的问题?(记忆集和卡集)
这部分内容主要是为了稍后介绍各款垃圾收集器时做前置知识铺垫,如果对这部分内容感到枯燥或者疑惑,可以先放下看,等后续遇到要使用它们的实际场景、实际问题时再结合问题,再回来阅读和理解。 记忆集和卡集 前面在分代收集理论那…...
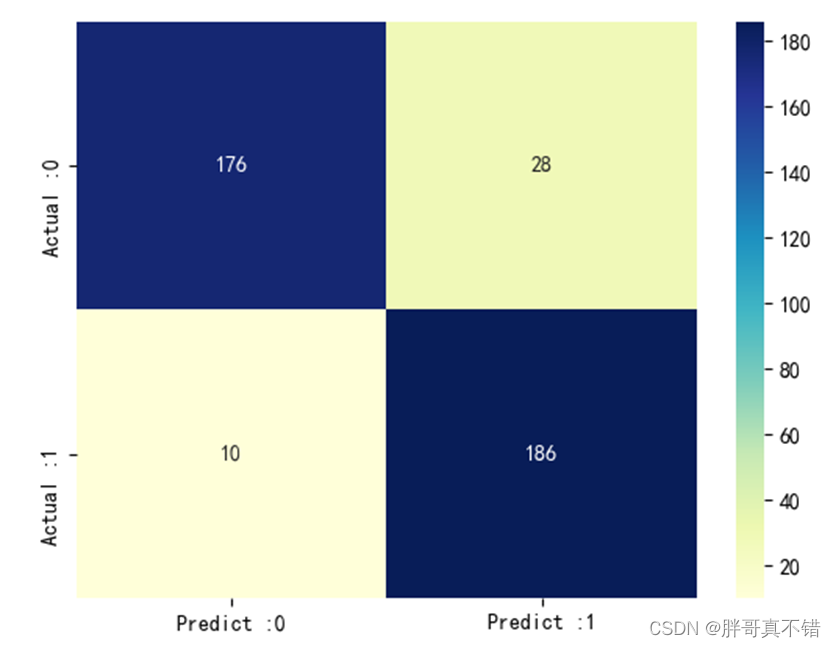
Python实现WOA智能鲸鱼优化算法优化卷积神经网络分类模型(CNN分类算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 鲸鱼优化算法 (whale optimization algorithm,WOA)是 2016 年由澳大利亚格里菲斯大学的Mirjalili 等提…...

使用 Qt 实现监听网页是否响应,导出 Excel 表
Qt 实现监听网页是否响应 要使用 Qt 实现监听网页是否响应,可以利用 QNetworkAccessManager 类来发送 HTTP 请求并处理响应。以下是一个示例代码: #include <QtNetwork>int main(int argc, char *argv[]) {QCoreApplication a(argc, argv);// 创…...

Java通过JNI技术调用C++动态链接库的helloword测试
JNI调用原理 原理就不细说了,其实就是写个库给Java调,可以百度一下Java JNI,下面是HelloWorld代码测试 编写一个本地测试类 package com.my.study.cpp_jni;/*** 测试Java调用C库* <p>使用命令javac -h . NativeTest.java自动生成C头…...

Python爬虫所需的常用库
爬虫是指通过程序自动访问互联网上的各种网站,并从网站上抓取所需的数据。Python作为一门强大的编程语言,拥有丰富的库和工具,使得编写爬虫变得更加容易和高效。本文将介绍一些Python爬虫中常用的库,包括网络请求库、解析库、数据…...
Android Studio真机运行时提示“安装失败”
用中兴手机真机运行没问题,用Vivo运行就提示安装失败。前提,手机已经打开了调试模式。 报错 Android Studio报错提示: Error running app The application could not be installed: INSTALL_FAILED_TEST_ONLY 手机报错提示: 修…...
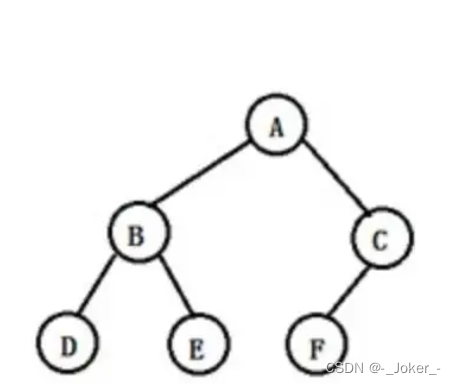
【C语言数据结构————————二叉树】
文章目录 文章目录 一、什么是树 树的定义 树的种类 树的深度 树的基本术语 二、满二叉树 定义 满二叉树的特点 三、完全二叉树 定义 特点 四、二叉树的性质 五、二叉树的存储结构 顺序存储结构 链式存储结构 六、二叉树的基本操作 七、二叉树的创建 八、二叉树…...
分组取每组数据的最大值和最小值的方法思路,为类似场景的数据分析提取提供思路,例如提取宗地内建筑的最高层数等可参考此方法思路
目录 一、实现效果 二、实现过程 1.读取并剔除无效数据 2.数据分组 3.提取最大值 4.提取最小值 三、总结 使用FME实现批量分组取每组数据的最大值和最小值,为类似场景的数据分析提取提供思路,例如提取宗地内建筑的最高层数等可参考此方法思路。关…...
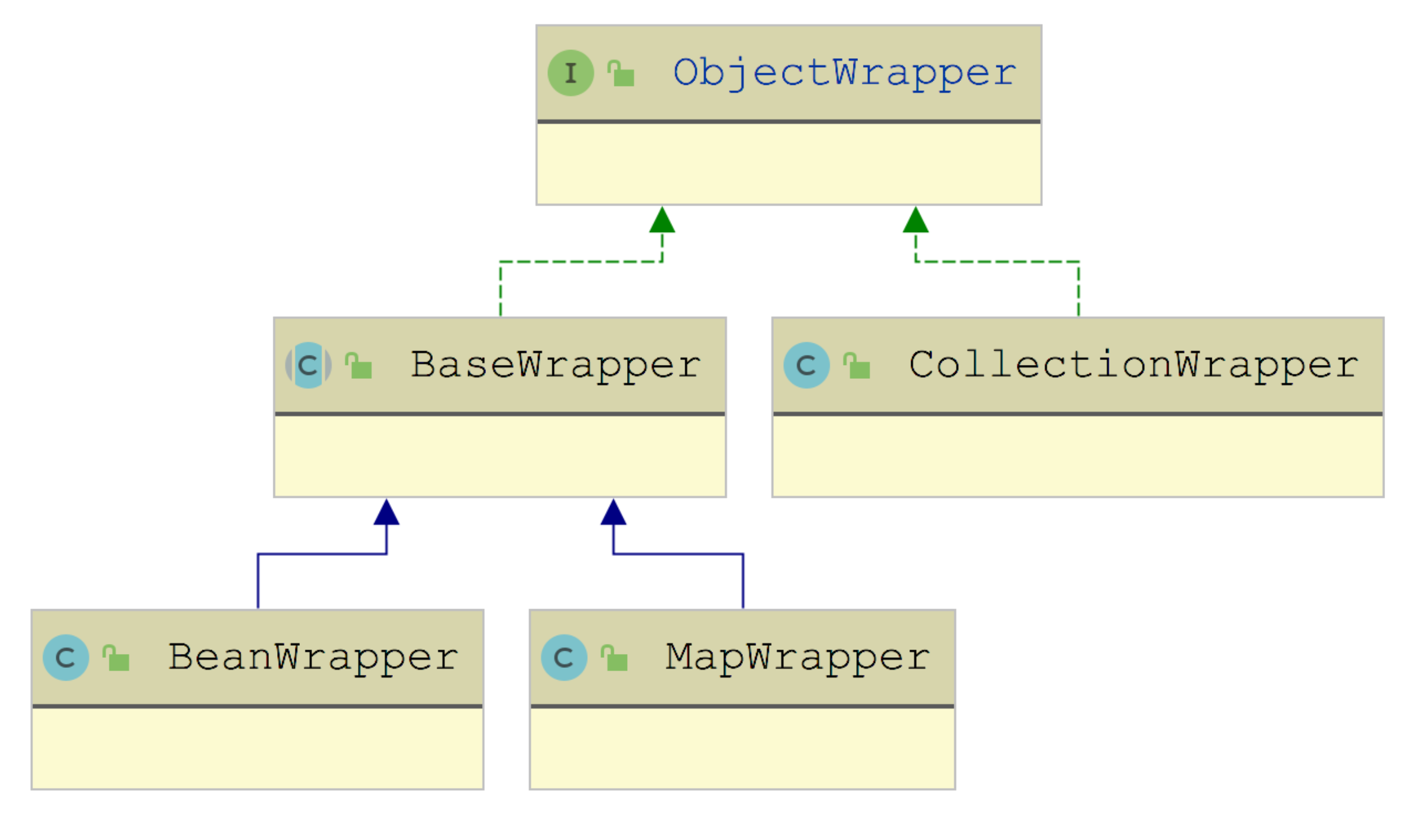
MyBatis 反射工具箱:带你领略不一样的反射设计思路
反射是 Java 世界中非常强大、非常灵活的一种机制。在面向对象的 Java 语言中,我们只能按照 public、private 等关键字的规范去访问一个 Java 对象的属性和方法,但反射机制可以让我们在运行时拿到任何 Java 对象的属性或方法。 有人说反射打破了类的封装…...
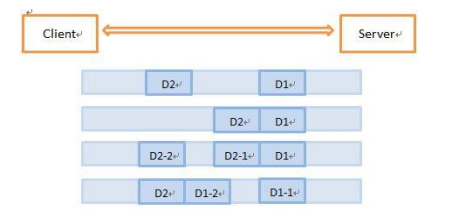
Netty第三部
继续Netty第二部的内容 一、ChannelHandler 1、ChannelHandler接口 ChannelHandler是Netty的主要组件,处理所有的入站和出站数据的应用程序逻辑的容器,可以应用在数据的格式转换、异常处理、数据报文统计等 继承ChannelHandler的两个子接口ÿ…...

【C++入门篇】保姆级教程篇【下】
目录 一、运算符重载 1)比较、赋值运算符重载 2) 流插入留提取运算符重载 二、剩下的默认成员函数 1)赋值运算符重载 2)const成员函数 3)取地址及const取地址操作符重载 三、再谈构造函数 1)初始化列表 …...

CCLink转Modbus TCP网关_CCLINK参数配置
CCLink转Modbus TCP网关(XD-ETHCL20),具有CCLINK主从站功能。主要用途是将各种MODBUS-TCP设备接入到CCLINK总线中。它可以作为从站连接到CCLINK总线上,也可以作为主站或从站连接到MODBUS-MTP总线上。 1、 配置网关的CCLINK参数&am…...
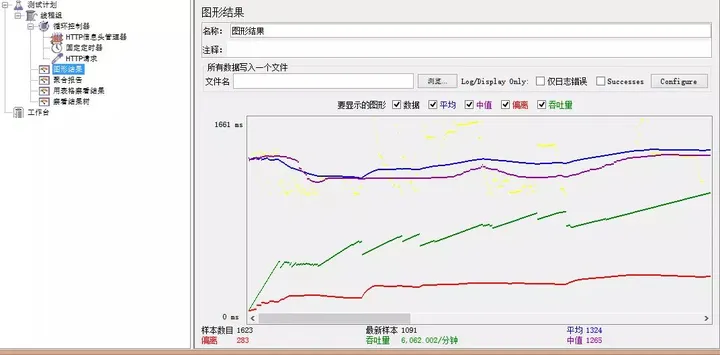
一文2000字从0到1使用压测神器JMeter进行压力测试!
概 述 Apache JMeter 是 Apache组织开发的基于 Java的压力测试工具。用于对软件做压力测试,它最初被设计用于 Web应用测试但后来扩展到其他测试领域。它可以用于测试静态和动态资源例如静态文件、Java 小服务程序、CGI 脚本、Java 对象、数据库, FTP 服…...

极狐GitLab CI 助力 .Net 项目研发效率和质量双提升
目录 .NET nuget 自动生成测试包(prerelease)版本号 .NET 版本号规范 持续集成自动打包 持续集成自动修改版本号 .NET 行级增量代码规范——拯救老项目 本地全量代码规范 行级增量代码规范 很多团队或开发者都会使用 C#、VB 等语言开发 .Net 应用…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
