【算法优选】 动态规划之斐波那契数列模型
文章目录
- 🎋前言
- 🍀[第 N 个泰波那契数](https://leetcode.cn/problems/n-th-tribonacci-number/)
- 🚩题目描述
- 🚩算法流程
- 🚩代码实现
- 🎄[使用最小花费爬楼梯](https://leetcode.cn/problems/min-cost-climbing-stairs/)
- 🚩题目描述
- 🚩算法思路
- 🎈解法⼀:
- 🎈解法⼆:
- 🚩代码实现:
- 解法一:
- 解法二:
- 🌲[解码方法](https://leetcode.cn/problems/decode-ways/submissions/)
- 🚩题目描述
- 🚩算法思路
- 🚩代码实现
- ⭕总结
🎋前言
动态规划相关题目都可以参考以下五个步骤进行解答:
-
状态表⽰
-
状态转移⽅程
-
初始化
-
填表顺序
-
返回值
后面题的解答思路也将按照这五个步骤进行讲解。
🍀第 N 个泰波那契数
🚩题目描述
泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数 n,请返回第 n 个泰波那契数 Tn 的值。
-
示例 1:
输入:n = 4
输出:4
解释:
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4 -
示例 2:
输入:n = 25
输出:1389537
class Solution {public int tribonacci(int n) {}
}
🚩算法流程
- 状态表⽰:
这道题可以「根据题⽬的要求」直接定义出状态表⽰:
dp[i] 表⽰:第 i 个泰波那契数的值。
- 状态转移⽅程:
题⽬已经⾮常贴⼼的告诉我们了:
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]
- 初始化:
从我们的递推公式可以看出, dp[i] 在 i = 0 以及 i = 1 的时候是没有办法进⾏推导的,因为 dp[-2] 或 dp[-1] 不是⼀个有效的数据。因此我们需要在填表之前,将 0, 1, 2 位置的值初始化。题⽬中已经告诉我们 dp[0] = 0,dp[1] = dp[2] = 1 。
- 填表顺序:
毫⽆疑问是「从左往右」。
- 返回值:
应该返回 dp[n] 的值。
🚩代码实现
class Solution {public int tribonacci(int n) {int[] dp = new int[n + 3];dp[0] = 0;dp[1] = 1;dp[2] = 1;for(int i = 0; i < n; i++) {dp[i + 3] = dp[i] + dp[i + 1] + dp[i + 2];}return dp[n];}
}
🎄使用最小花费爬楼梯
🚩题目描述
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
- 示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
-支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。 - 示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
-支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
-支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
-支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
-支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
-支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
-支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
class Solution {public int minCostClimbingStairs(int[] cost) {}
}
🚩算法思路
🎈解法⼀:
- 状态表⽰:
这道题可以根据「经验+题⽬要求」直接定义出状态表⽰:
第⼀种:以 i 位置为结尾,然后一系列操作
dp[i] 表⽰:到达 i 位置时的最⼩花费。(注意:到达 i 位置的时候, i 位置的钱不需要算上)
- 状态转移⽅程:
根据最近的⼀步,分情况讨论:
▪ 先到达 i - 1 的位置,然后⽀付 cost[i - 1] ,接下来⾛⼀步⾛到 i 位置:dp[i - 1] + csot[i - 1] ;
▪ 先到达 i - 2 的位置,然后⽀付 cost[i - 2] ,接下来⾛⼀步⾛到 i 位置:dp[i - 2] + csot[i - 2] 。
- 初始化:
从我们的递推公式可以看出,我们需要先初始化 i = 0 ,以及 i = 1 位置的值。容易得到 dp[0] = dp[1] = 0 ,因为不需要任何花费,就可以直接站在第 0 层和第 1 层上。
- 填表顺序:
根据「状态转移⽅程」可得,遍历的顺序是「从左往右」。
- 返回值:
根据「状态表⽰以及题⽬要求」,需要返回 dp[n] 位置的值。
🎈解法⼆:
- 状态表⽰:
这道题可以根据「经验+题⽬要求」直接定义出状态表⽰:第⼆种:以 i 位置为起点,进行一系列操作。
dp[i] 表⽰:从 i 位置出发,到达楼顶,此时的最⼩花费。
- 状态转移⽅程:
根据最近的⼀步,分情况讨论:
▪ ⽀付 cost[i] ,往后⾛⼀步,接下来从 i + 1 的位置出发到终点: dp[i + 1] + cost[i] ;
▪ ⽀付 cost[i] ,往后⾛两步,接下来从 i + 2 的位置出发到终点: dp[i + 2] + cost[i] ;
我们要的是最⼩花费,因此 dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i] 。
- 初始化:
为了保证填表的时候不越界,我们需要初始化最后两个位置的值,结合状态表⽰易得: dp[n - 1] = cost[n - 1], dp[n - 2] = cost[n - 2]
- 填表顺序:
根据「状态转移⽅程」可得,遍历的顺序是「从右往左」。
- 返回值:
根据「状态表⽰以及题⽬要求」,需要返回 dp[n] 位置的值。也就是dp[0]与dp[1]中的较小值
🚩代码实现:
解法一:
class Solution {public int minCostClimbingStairs(int[] cost) {int n = cost.length;int[] dp = new int[n + 1];for(int i = 2; i <= n; i++) {dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[n];}
}
解法二:
class Solution {public int minCostClimbingStairs(int[] cost) {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回值int n = cost.length;int[] dp = new int[n];dp[n - 1] = cost[n - 1]; dp[n - 2] = cost[n - 2];for(int i = n - 3; i >= 0; i--) {dp[i] = Math.min(dp[i + 1], dp[i + 2]) + cost[i];}return Math.min(dp[0], dp[1]);}
}
🌲解码方法
🚩题目描述
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
‘A’ -> “1”
‘B’ -> “2”
…
‘Z’ -> “26”
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,“11106” 可以映射为:
“AAJF” ,将消息分组为 (1 1 10 6)
“KJF” ,将消息分组为 (11 10 6)
注意,消息不能分组为 (1 11 06) ,因为 “06” 不能映射为 “F” ,这是由于 “6” 和 “06” 在映射中并不等价。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。
题目数据保证答案肯定是一个 32 位 的整数。
-
示例 1:
输入:s = “12”
输出:2
解释:它可以解码为 “AB”(1 2)或者 “L”(12)。 -
示例 2:
输入:s = “226”
输出:3
解释:它可以解码为 “BZ” (2 26), “VF” (22 6), 或者 “BBF” (2 2 6) 。 -
示例 3:
输入:s = “06”
输出:0
解释:“06” 无法映射到 “F” ,因为存在前导零(“6” 和 “06” 并不等价)。
class Solution {public int numDecodings(String s) {}
}
🚩算法思路
类似于斐波那契数列~
- 状态表⽰:
根据以往的经验,对于⼤多数线性 dp ,我们经验上都是「以某个位置结束或者开始」做⽂章,这⾥我们继续尝试「⽤i位置为结尾」结合「题⽬要求」来定义状态表⽰。dp[i] 表⽰:字符串中 [0,i] 区间上,⼀共有多少种编码⽅法。
- 状态转移⽅程:
定义好状态表⽰,我们就可以分析 i 位置的 dp 值,如何由「前⾯」或者「后⾯」的信息推导出
来。
关于 i 位置的编码状况,我们可以分为下⾯两种情况:
- 让 i 位置上的数单独解码成⼀个字⺟;
- 让 i 位置上的数与 i - 1 位置上的数结合,解码成⼀个字⺟。
下⾯我们就上⾯的两种解码情况,继续分析:
-
- 让i位置上的数单独解码成⼀个字⺟,就存在「解码成功」和「解码失败」两种情况:
-
-
- 解码成功:当 i 位置上的数在 [1, 9] 之间的时候,说明 i 位置上的数是可以单独解码的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 1] 区间上的解码⽅法。因为 [0, i - 1] 区间上的所有解码结果,后⾯填上⼀个 i 位置解码后的字⺟就可以了。此时 dp[i] = dp[i - 1] ;
-
-
-
- 解码失败:当 i 位置上的数是 0 的时候,说明 i 位置上的数是不能单独解码的,那么此时 [0, i] 区间上不存在解码⽅法。因为 i 位置如果单独参与解码,但是解码失败了,那么前⾯做的努⼒就全部⽩费了。此时 dp[i] = 0 。
-
-
- 让 i 位置上的数与 i - 1 位置上的数结合在⼀起,解码成⼀个字⺟,也存在「解码成功」和「解码失败」两种情况:
-
-
- 解码成功:当结合的数在 [10, 26] 之间的时候,说明 [i - 1, i] 两个位置是可以解码成功的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 2 ]区间上的解码⽅法,原因同上。此时dp[i] = dp[i - 2] ;
-
-
-
- 解码失败:当结合的数在 [0, 9] 和 [27 , 99] 之间的时候,说明两个位置结合后解码失败(这⾥⼀定要注意 00 01 02 03 04 …这⼏种情况),那么此时 [0, i] 区间上的解码⽅法就不存在了,原因依旧同上。此时 dp[i] = 0 。
-
综上所述: dp[i] 最终的结果应该是上⾯四种情况下,解码成功的两种的累加和(因为我们关⼼的是解码⽅法,既然解码失败,就不⽤加⼊到最终结果中去),因此可以得到状态转移⽅程( dp[i] 默认初始化为 0 ):
- 当 s[i] 上的数在 [1, 9] 区间上时: dp[i] += dp[i - 1] ;
- 当 s[i - 1] 与 s[i] 上的数结合后,在 [10, 26] 之间的时候: dp[i] += dp[i - 2] ;
如果上述两个判断都不成⽴,说明没有解码⽅法, dp[i] 就是默认值 0 。
- 初始化:
- ⽅法⼀(直接初始化):
由于可能要⽤到 i - 1 以及 i - 2 位置上的 dp 值,因此要先初始化「前两个位置」。
初始化 dp[0] : -
- 当 s[0] == ‘0’ 时,没有编码⽅法,结果 dp[0] = 0 ;
-
- 当 s[0] != ‘0’ 时,能编码成功, dp[0] = 1
初始化 dp[1] :
-
- 当 s[1] 在 [1,9] 之间时,能单独编码,此时 dp[1] += dp[0] (原因同上,dp[1] 默认为 0 )
-
- 当 s[0] 与 s[1] 结合后的数在 [10, 26] 之间时,说明在前两个字符中,⼜有⼀种编码⽅式,此时 dp[1] += 1
-
⽅法⼆(添加辅助位置初始化):
可以在最前⾯加上⼀个辅助结点,帮助我们初始化。使⽤这种技巧要注意两个点: -
- 辅助结点⾥⾯的值要保证后续填表是正确的;
-
- 下标的映射关系
- 填表顺序:
毫⽆疑问是「从左往右」
- 返回值:
应该返回 dp[n - 1] 的值,表⽰在 [0, n - 1] 区间上的编码⽅法。
🚩代码实现
class Solution {public int numDecodings(String ss) {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回值int n = ss.length();char[] s = ss.toCharArray();int[] dp = new int[n];if(s[0] != '0') {dp[0] = 1; // 初始化第⼀个位置}if(n == 1) {return dp[0]; // 处理边界情况}// 初始化第⼆个位置if(s[1] != '0' && s[0] != '0') {dp[1] += 1;}int t = (s[0] - '0') * 10 + s[1] - '0';if(t >= 10 && t <= 26) {dp[1] += 1;}for(int i = 2; i < n; i++) {// 先处理第⼀种情况if(s[i] != '0') {dp[i] += dp[i - 1];}// 处理第⼆种情况int tt = (s[i - 1] - '0') * 10 + s[i] - '0';if(tt >= 10 && tt <= 26) {dp[i] += dp[i - 2];}}return dp[n - 1];}
}
代码优化如下:
class Solution {public int numDecodings(String ss) {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回值int n = ss.length();char[] s = ss.toCharArray();int[] dp = new int[n + 1];dp[0] = 1; // 保证后续填表是正确的if(s[1 - 1] != '0') dp[1] = 1;for(int i = 2; i <= n; i++) {// 先处理第⼀种情况if(s[i - 1] != '0') {dp[i] += dp[i - 1];}// 处理第⼆种情况int tt = (s[i - 2] - '0') * 10 + s[i - 1] - '0';if(tt >= 10 && tt <= 26) {dp[i] += dp[i - 2]; }}return dp[n];}
}
⭕总结
关于《【算法优选】 动态规划之斐波那契数列模型》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!
相关文章:

【算法优选】 动态规划之斐波那契数列模型
文章目录 🎋前言🍀[第 N 个泰波那契数](https://leetcode.cn/problems/n-th-tribonacci-number/)🚩题目描述🚩算法流程🚩代码实现 🎄[使用最小花费爬楼梯](https://leetcode.cn/problems/min-cost-climbing…...
FreeRTOS知识梳理
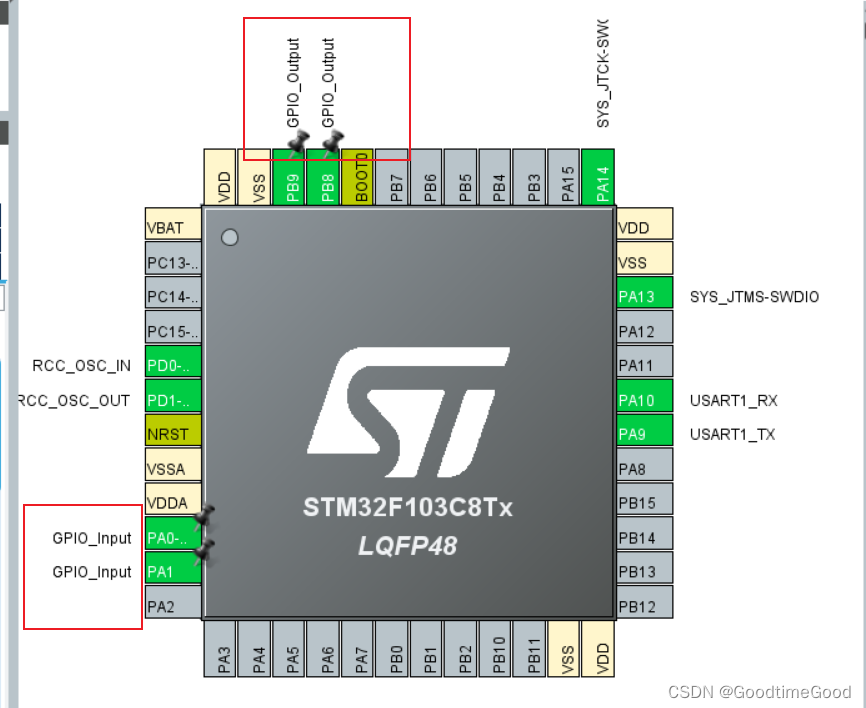
一、RTOS:Real time operating system,中文意思为 实时操作系统,它是一类操作系统,比如uc/OS、FreeRTOS、RTX、RT-Thread 这些都是实时操作系统。 二、移植FreeRTOS到STM32F103C8T6上 interface选择CMSIS_V1,RCC选择Crystal Ceramic Resonator 。 …...
)
冒泡排序算法(C++版)
1、什么是冒泡排序? 冒泡排序(Bubble Sort)是一种简单的排序算法,其基本思想是多次遍历待排序的元素序列,每次比较相邻两个元素,如果它们的顺序不正确就交换它们,直到整个序列有序。在每一轮遍…...

第22章_数据库的设计规范
文章目录 范式的概念三范式范式一范式二范式三 反范式总结 范式的概念 为了建立冗余较小、结构合理的数据库,设计数据库时必须遵循一定的规则。在关系型数据库中这种规则就称为范式。范式是符合某一种设计要求的总结。要想设计一个结构合理的关系型数据库ÿ…...

5. 深度学习——正则化
机器学习面试题汇总与解析——正则化 本章讲解知识点 什么是正则化为什么要使用正则化?详细讲解正则化本专栏适合于Python已经入门的学生或人士,有一定的编程基础。本专栏适合于算法工程师、机器学习、图像处理求职的学生或人士。本专栏针对面试题答案进行了优化,尽量做到好…...

【链表和顺序表的优缺点】
...

iOS移动应用安全加固:保护您的App免受恶意攻击的重要步骤
目录 iOS移动应用安全加固:保护您的App免受恶意攻击的重要步骤 摘要 引言 一、APP加固的概念 二、APP加固方案的比较 三、保护iOS应用的安全 四、总结 参考资料 摘要 本文介绍了移动应用程序(App)加固的概念和流程,以及市…...

C# .NET Core API 注入Swagger
C# .NET Core API 注入Swagger 环境 Windows 10Visual Studio 2019(2017就有可以集中发布到publish目录的功能了吧)C#.NET Core 可跨平台发布代码,超级奈斯NuGet 套件管理dll将方法封装(据说可以提高效率,就像是我们用的dll那种感觉)Swagger 让接口可视化编写时间2020-12-09 …...

家庭安全计划 挑战赛| 溺水预防
溺水预防 从了解到行动 家庭安全计划 | 少年急救官 地震避险逃生该怎么做? 起火了该如何应对? 哪些行为容易导致溺水? 家庭风险隐患有哪些? 家庭逃生演练四步骤你会吗? 国际救助儿童会(英国ÿ…...

飞书开发学习笔记(五)-Python快速开发网页应用
飞书开发学习笔记(五)-Python快速开发网页应用 一.下载示例代码 首先进入飞书开放平台: https://open.feishu.cn/app 凭证与基础信息 页面,在 应用凭证 中获取 App ID 和 App Secret 值。 教程和示例代码位置:https://open.feishu.cn/document/home/integrating-…...

对测试职业发展的思考
虽然在测试行业摸爬滚打了很年,随着年龄的增长,职位的升迁,似乎已经走到了尽头,因而还是时不时觉得自己的职业发展目标很模糊,这是最近对自己职业发展的一些思考,希望与大家进行分享和探讨: 1、…...
博弈论入门
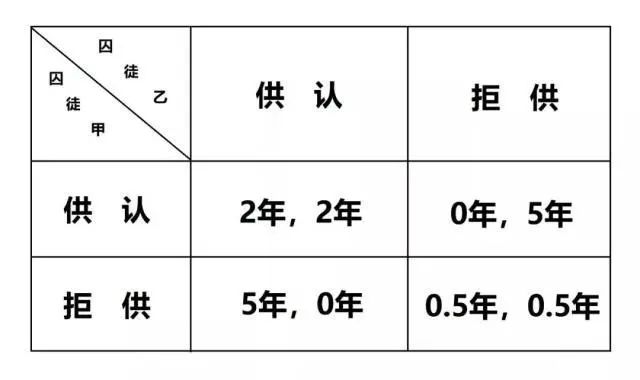
目录 什么是博弈? 博弈论的发展历史? 博弈的要素有哪些? 博弈的分类? 博弈论的应用 收益矩阵 纳什均衡的定义 博弈论的例子 1、田忌赛马 2、穷途困境 2.1优化反应函数法 2.2Nashpy库 2.3顶点枚举算法 3、Nash游戏 …...

php加密解密
public static function encrypt($data, $key) {$key 111;// 生成盐值$salt openssl_random_pseudo_bytes(16);// 使用盐值和密钥进行加密$encrypted openssl_encrypt($data, AES-128-CBC, $key, 0, $salt);// 将盐值和加密后的数据拼接$result base64_encode($salt . $enc…...

基于YOLOv8的输电线路异物识别算法应用
基于 YOLOv8 的输电线路异物识别算法应用 输电线路作为电力系统的重要一环,保证其安全稳定运行是十分必要的。由于长期暴露于室外,线路所面临的不安全因素繁多,异物入侵便是其中之一。异物可能会引起线路短路甚至诱发火灾,因此要加…...
win环境Jenkins部署前端项目
今天分享win环境Jenkins部署前端vue项目,使用的版本jenkins版本Jenkins 2.406版本。 前提是jenkins安装好了,通用配置已经配置好了,可以参考上两篇博客。 1、前端项目依赖nodejs,需要安装相关插件 点击进入 安装成功标准 jenki…...

DDD领域驱动设计模式结构图面向接口编程
DDD领域驱动设计模式结构图面向接口编程 9.资源库 在刚接触资源库(Repository)时,第一反应便是这就是个 DAO 层,访问数据库,然后吧啦吧啦,但是,当接触的越久,越发认识到第一反应是错的,资源库更…...

Ubuntu中安装R语言环境并在jupyter kernel里面增加R kernel
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️ 👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
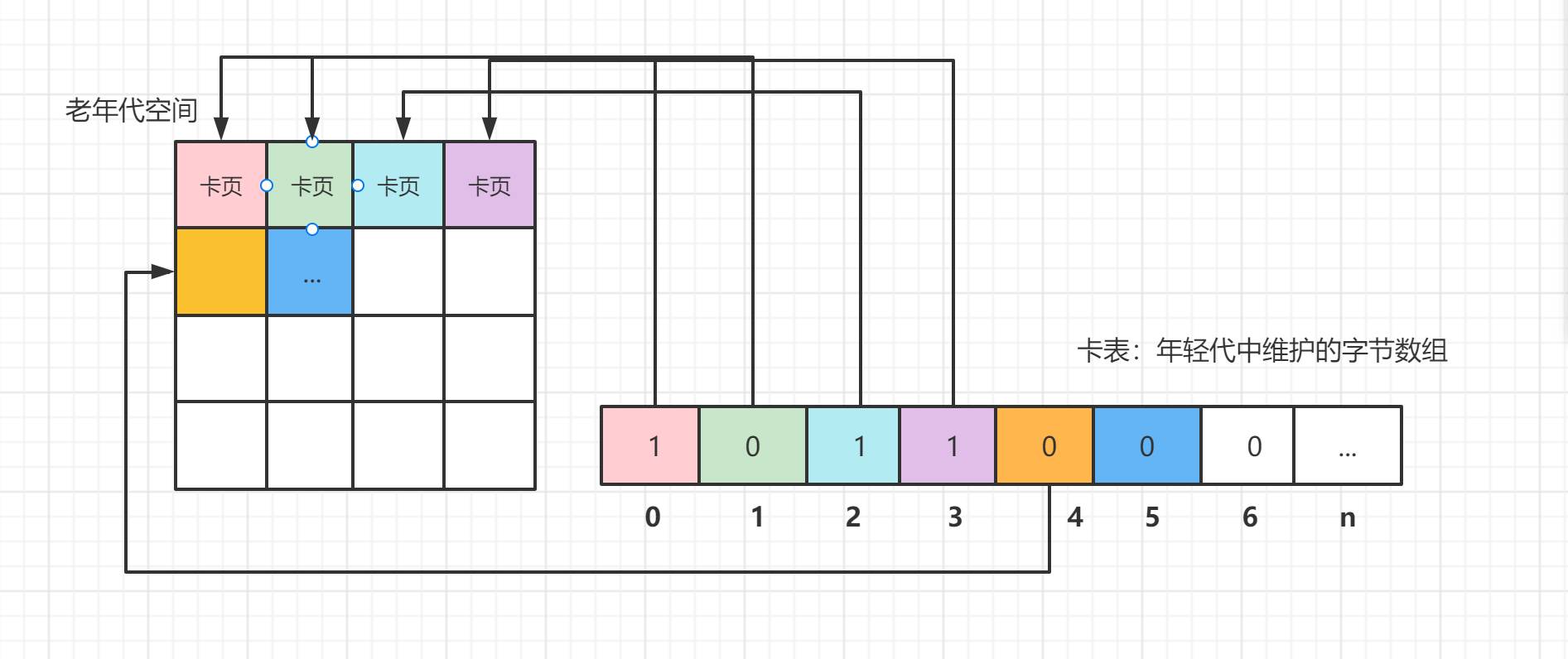
JVM:如果是你,你如何解决跨代引用的问题?(记忆集和卡集)
这部分内容主要是为了稍后介绍各款垃圾收集器时做前置知识铺垫,如果对这部分内容感到枯燥或者疑惑,可以先放下看,等后续遇到要使用它们的实际场景、实际问题时再结合问题,再回来阅读和理解。 记忆集和卡集 前面在分代收集理论那…...
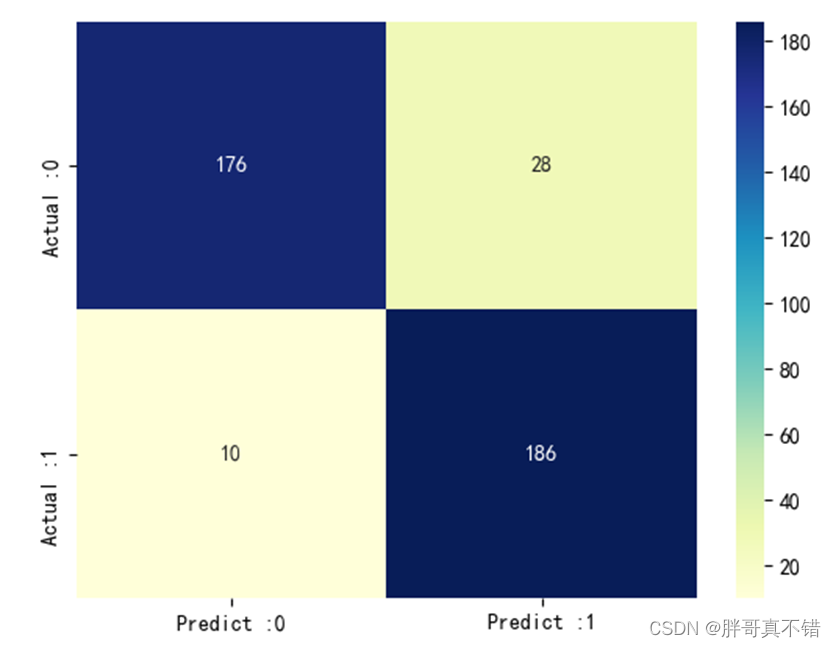
Python实现WOA智能鲸鱼优化算法优化卷积神经网络分类模型(CNN分类算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 鲸鱼优化算法 (whale optimization algorithm,WOA)是 2016 年由澳大利亚格里菲斯大学的Mirjalili 等提…...

使用 Qt 实现监听网页是否响应,导出 Excel 表
Qt 实现监听网页是否响应 要使用 Qt 实现监听网页是否响应,可以利用 QNetworkAccessManager 类来发送 HTTP 请求并处理响应。以下是一个示例代码: #include <QtNetwork>int main(int argc, char *argv[]) {QCoreApplication a(argc, argv);// 创…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
