数据结构—二叉树的模拟实现(c语言)
目录
一.前言
二.模拟实现链式结构的二叉树
2.1二叉树的底层结构
2.2通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
2.3二叉树的销毁
2.4二叉树查找值为x的节点
2.5二叉树节点个数
2.6二叉树叶子节点个数
2.7二叉树第k层节点个数
三.二叉树的遍历
3.1前序遍历
3.2中序遍历
3.3后序遍历
3.4层序遍历
一.前言
详解—数据结构《树和二叉树》-CSDN博客
上一节课我们详解了树和二叉树,这一篇博客我来带领大家来模拟实现二叉树
二.模拟实现链式结构的二叉树
2.1二叉树的底层结构
首先,有一个数据域
然后有俩个二叉树指针,分别指向他们的左孩子和右孩子
typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;2.2通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
1、按照前序遍历(先走根,再走左子树,再走右子树)的方法,我们首先了解大概思路
2、数组里面的#就相当于为空,所以,我们先判断if 我们的数组为#,就返回空
3、然后我们创建一个节点,如果开辟失败,返回空,我们进行判断
4、然后放入数据,
5、再然后递归开始走左子树,右子树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int * pi)
{if ('#' == a[*pi]){++(*pi);return NULL;}BTNode * root = (BTNode *)malloc (sizeof(BTNode));if (root == NULL){perror("malloc");return;}root->data = a[(*pi)++];root->left = BinaryTreeCreate(a, n, pi);root->right = BinaryTreeCreate(a, n, pi);return root;
}
2.3二叉树的销毁
销毁一颗二叉树
1.首先判断如果是空树,直接返回
2.利用递归从最左边的树开始进行一个节点一个节点的删除
void BinaryTreeDestory(BTNode** root)
{if (*root == NULL)return;BinaryTreeDestory((*root)->left);BinaryTreeDestory((*root)->right);free(*root);*root = NULL;
}
2.4二叉树查找值为x的节点
二叉树的查找在这里我用的前序遍历递归
1.先确定递归的退出条件,root等于空就返回
2.然后进行前序遍历
3.判断一下当前节点是不是x
4.在开始走左子树
5.开始走右子树
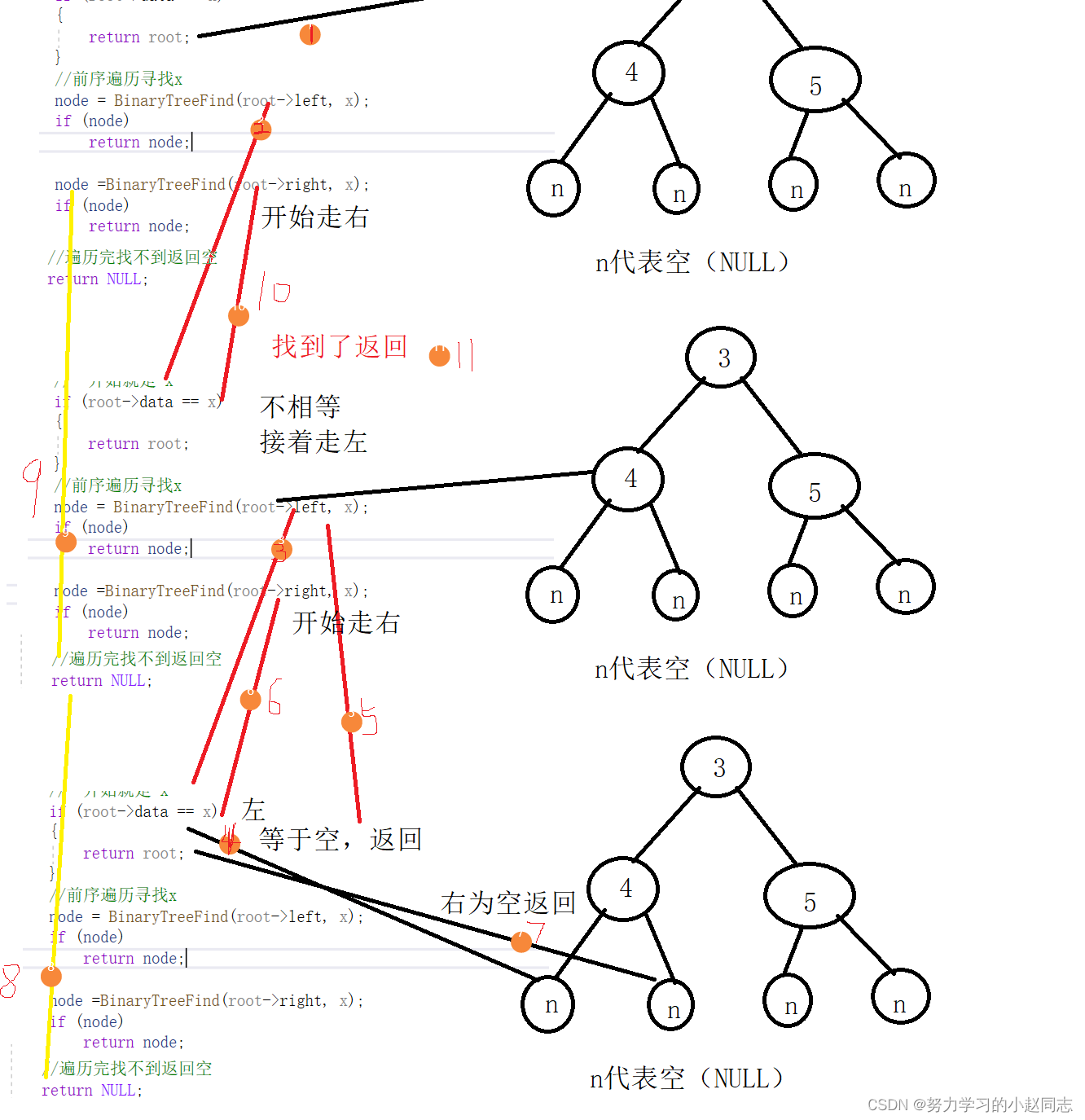
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{BTNode* node;if (root == NULL)return NULL ;//一开始就是 xif (root->data == x){return root;}//前序遍历寻找xnode = BinaryTreeFind(root->left, x);if (node)return node;node =BinaryTreeFind(root->right, x);if (node)return node;//遍历完找不到返回空return NULL;
}
2.5二叉树节点个数
二叉树的节点个数就是二叉树,左子树加上右子树加上根
这里我用的也是递归的方法,同学们可以看一下
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right) + 1;
}2.6二叉树叶子节点个数
叶节点或终端节点:度为0的节点称为叶节点;
可以观看上一篇文章取了解叶子节点
详解—数据结构《树和二叉树》-CSDN博客
查找叶子节点,也是用的递归方法,
首先,增加递归退出条件root==0
然后,如果所在的节点他的左右子树都为空,那么他就是叶子节点,返回1
最后递归遍历所有的叶子节点进行相加
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}2.7二叉树第k层节点个数
在二叉树中我们想知道,每一层有多少个节点
1.确定递归退出条件
2.如果k=1,返回1,代表找到了这一层的一个节点
3.进行递归,每一层k-1,当k=1是找到所在k层,返回一,进行相加查找当前层数据
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) +BinaryTreeLevelKSize(root->right, k - 1);}三.二叉树的遍历
3.1前序遍历
二叉树的遍历了解可以详细看看上一章节
详解—数据结构《树和二叉树》-CSDN博客
前序遍历的遍历方法,就是先走根然后左子树,右子树
我们这里还是用的递归
1.先确定递归条件
2.打印当前节点
3.走左子树
4.走右子树
void BinaryTreePrevOrder(BTNode * root)
{if (root == NULL){return;}printf("%c ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}3.2中序遍历
中序遍历的顺序是先走左子树,再走根,再走右子树
我们的实现方法如下:
1.确定递归条件
2.走左子树
3.打印当前节点
4.走右子树
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){return;}BinaryTreeInOrder(root->left);printf("%c ", root->data);BinaryTreeInOrder(root->right);
}3.3后序遍历
后序遍历的顺序是先走左子树,再走右子树,再走根
我们的实现方法如下:
1.确定递归条件
2.走左子树
3.走右子树
4.打印当前节点
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%c ", root->data);
}3.4层序遍历
首先,我们层序遍历,需要用到队列,我们先添加前几章写的队列到当前项目中,然后进行调用
1.创建并初始化一个队列
2.当根不为空时,将根节点入队,
3.保存根节点地址,访问其数据域,之后出队;
4.若根节点的左子树不为空,入队左子树,
5.判断根节点的右子树不为空,入队右子树,
6.保存队头节点地址,访问其数据域,之后出队;
8.重复上述过程的条件是队列不为空
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;//初始化队列QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);printf("%c ", front->data);QueuePop(&q);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");//销毁队列QueueDestroy(&q);
}相关文章:

数据结构—二叉树的模拟实现(c语言)
目录 一.前言 二.模拟实现链式结构的二叉树 2.1二叉树的底层结构 2.2通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树 2.3二叉树的销毁 2.4二叉树查找值为x的节点 2.5二叉树节点个数 2.6二叉树叶子节点个数 2.7二叉树第k层节点个数 三.二叉树的遍历 3.1…...

COCO数据集下载
文章目录 COCO官网貌似全部失效百度网盘提取码一直是1152 COCO官网 官网下载 train2017.zip annotations_trainval2017.zip val2017.zip stuff_annotations_trainval2017.zip test2017.zip image_info_test2017.zip 貌似全部失效 百度网盘提取码一直是1152 stuff_annotatio…...
基于安卓android微信小程序的校园互助平台
项目介绍 随着社会的发展,社会的方方面面都在利用信息化时代的优势。互联网的优势和普及使得各种系统的开发成为必需。 本文以实际运用为开发背景,运用软件工程原理和开发方法,它主要是采用java语言技术和mysql数据库来完成对系统的设计。整…...
)
Spring整合Junit(4、5)
在之前的测试方法中,几乎都能看到以下的两行代码: ApplicationContext context new classPathXmlApplicationContext("xxx.xm"); XXXX XXX context.getBean(Xxxx.cTass); 这两行代码的作用是创建Spring容器,最终获取到对象,但是每…...
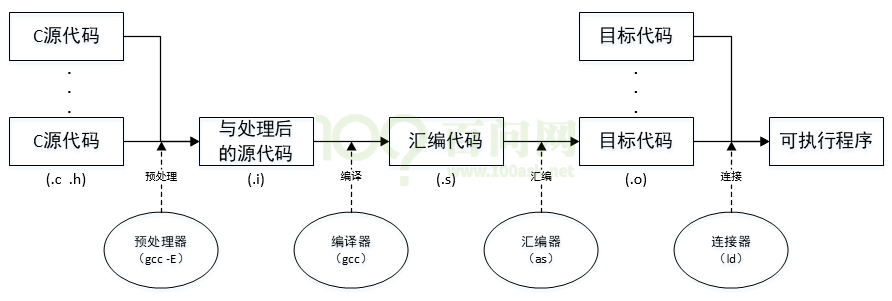
Linux 程序开发流程 / 基本开发工具 / Vim / GCC工具链 / Make 工具 / Makefile 模板
编辑整理 by Staok。 本文部分内容摘自 “100ask imx6ull” 开发板的配套资料(如 百问网的《嵌入式Linux应用开发完全手册》,在 百问网 imx6ull pro 开发板 页面 中的《2.1 100ASK_IMX6ULL_PRO:开发板资料》或《2.2 全系列Linux教程…...

2023.11.13【读书笔记】丨生物信息学与功能基因组学(第六章 多重序列比对 下)
目录 6.4 多重序列比对数据库6.5 基因组区域的多重序列比对6.6 展望6.7 常见问题总结 6.4 多重序列比对数据库 Pfam:基于谱隐马尔可夫模型构建的蛋白质家族数据库 SMART:简易分子构型研究工具,与细胞信号传导、细胞外结构域以及染色质功能…...
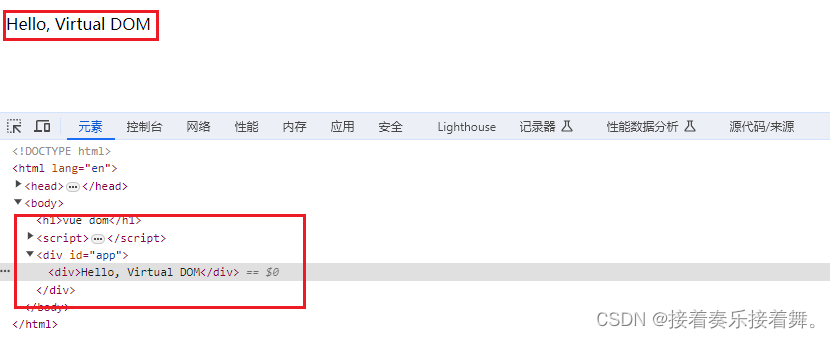
【vue】虚拟dom的原理是什么?手写实现虚拟dom !
1.虚拟dom的原理 虚拟 DOM 是对 DOM 的抽象,本质上就是用 JavaScript 对象来描述 DOM 结构。Vue.js 中关于虚拟 DOM 的实现主要进行了以下几个步骤: 1.生成虚拟 DOM: Vue.js 使用 render 函数来依据模板代码生成虚拟 DOM。在这个过程中&a…...
CentOS 7 双网卡绑定热备 —— 筑梦之路
为什么需要? 1. 增强网络的可靠性 2. 保障服务的可持续性 3. 降低网卡故障带来的不良影响 有哪些模式? 模式0:轮询策略(round robin),mode0,优点:流量提高一倍缺点:需要接…...

Qt绘制简单图表
Qt图表类似于model/view,chart就是model。 创建图表的各个部件: QChart *chart new QChart();chart->setTitle(tr("简单函数曲线")); // chart->setAcceptHoverEvents(true);ui->chartView->setChart(chart);ui->chartVi…...

CCLink转Modbus TCP网关_MODBUS网口设置
兴达易控CCLink转Modbus TCP网关是一种用于连接CCLink网络和Modbus TCP网络的设备。它提供了简单易用的MODBUS网口设置,可以帮助用户轻松地配置和管理网络连接 1 、网关做为MODBUS主站 (1)将电脑用网线连接至网关的P3网口上。 (…...

Vux购物车案例
一、综合案例 - 创建项目 本案例主要针对Vuex共享数据的练习以及父子组件数据的共享。 脚手架新建项目 (注意:勾选vuex) 版本说明: vue2 vue-router3 vuex3 vue3 vue-router4 vuex4/pinia vue create vue-cart-demo将原本src内容清空,替换…...
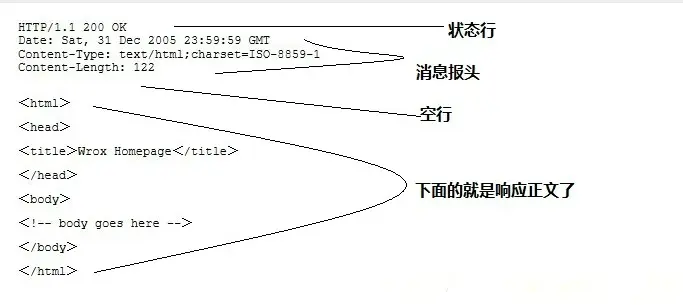
浅析网络协议-HTTP协议
1.HTTP简介 HTTP协议是Hyper Text Transfer Protocol(超文本传输协议)的缩写,是用于从万维网(WWW:World Wide Web )服务器传输超文本到本地浏览器的传送协议。 HTTP是一个基于TCP/IP通信协议来传递数据(HTML 文件, 图…...
启动Docker服务后显示Docker Engine stopped
1、重新启动Docker服务:打开Windows服务管理器(可以在开始菜单中搜索),找到"Docker Desktop Service"或类似命名的服务,右键单击并选择"重启"。稍等片刻,看看是否重新启动成功 2、尝试…...

Centos7 升级到 Centos8 教程以及关于dnf包管理工具的若干问题解决方案
目录 为什么升级一、参考文档二、升级步骤三、安装git编码错误缓存问题安装git依赖冲突问题解决办法 为什么升级 jenkins 2.4版本需要CentOS8 一、参考文档 点我 二、升级步骤 1.安装epel源 yum -y install epel-release2.安装rpmconf和yum-utils yum -y install rpmco…...

计算机网络技术(一)
深入浅出计算机网络 微课视频_哔哩哔哩_bilibili 第一章概述 1.1 信息时代的计算机网络 1. 计算机网络各类应用 2. 计算机网络带来的负面问题 3. 我国互联网发展情况 1.2 因特网概述 1. 网络、互连网(互联网)与因特网的区别与关系 如图所示࿰…...

redis监听key失效
前言 使用redis进行大数据量信息存储时,如存储百万级别设备/通道信息,如果我们想获取设备/通道是否失效,常规的方法是定时获取,但是这样对于应用来说太消耗性能。 redis提供了一种key事件监听的机制,应用可以监…...
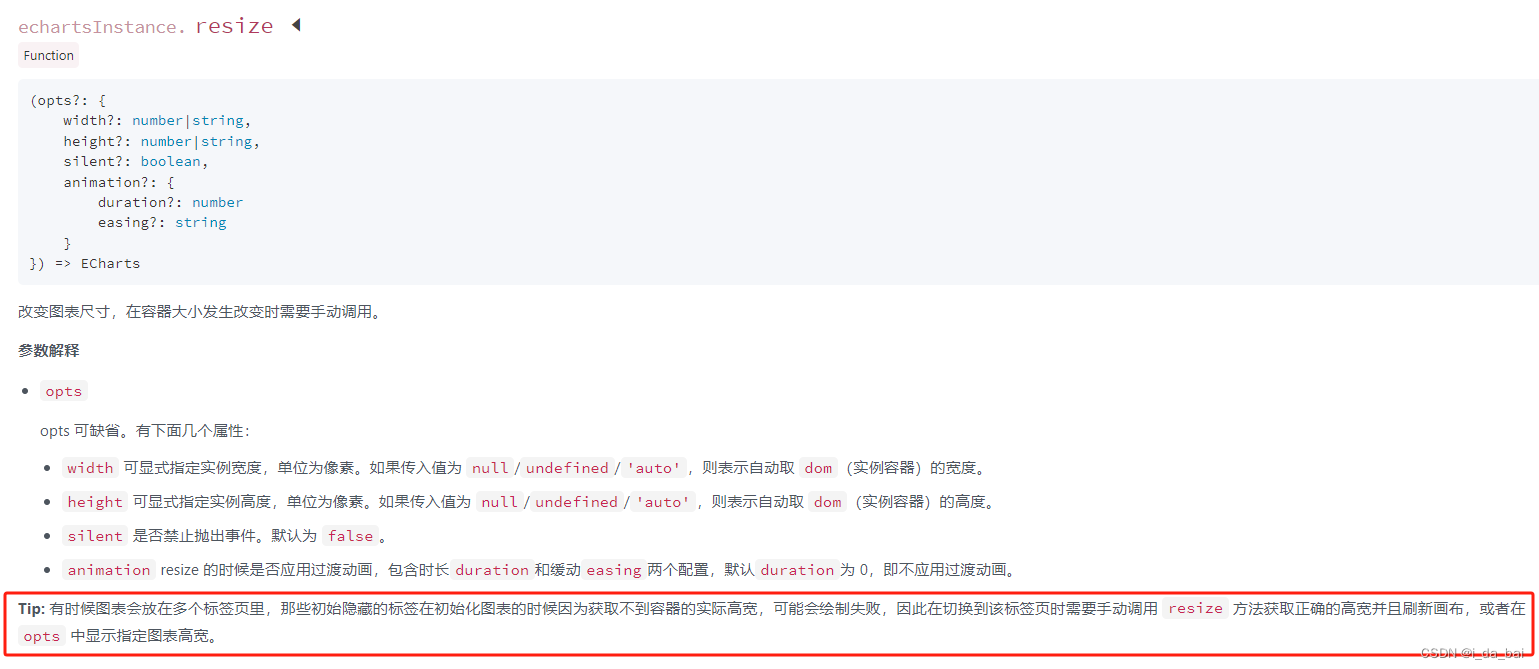
echart宽度100px原因(解决el-tabs里的echarts图表宽度不自适应,只有100px问题)
目录 问题描述产生原因处理方法1.使用echart 的API —— resize()2.使用 v-if 总结 问题描述 项目中在el-tabs下面使用了图表,发现图表的宽度始终只有100px 产生原因 首先echart初始化的组件宽度设置了width: 100%,那么本来这个时候,echar…...
【使用教程】在Ubuntu下PMM60系列一体化伺服电机通过PDO跑循环同步位置模式详解
本教程将指导您在Ubuntu操作系统下使用PDO来配置和控制PMM60系列一体化伺服电机以实现循环同步位置模式。我们将介绍必要的步骤和命令,以确保您能够成功地配置和控制PMM系列一体化伺服电机。 一、准备工作 在正式介绍之前还需要一些准备工作:1.装有lin…...
【机器学习】七、降维与度量学习
1. 维数灾难 样本的特征数称为维数(dimensionality),当维数非常大时,也就是现在所说的维数灾难。 维数灾难具体表现在:在高维情形下,数据样本将变得十分稀疏,因为此时要满足训练样本为“密采样…...

Yolov5 + 界面PyQt5 +.exe文件部署运行
介绍 Yolov5是一种基于深度学习的目标检测算法,PyQt5是一个Python编写的GUI框架,用于创建交互式界面。在部署和运行Yolov5模型时,结合PyQt5可以方便地创建一个用户友好的界面,并将代码打包为.exe文件以供其他人使用。 下面是一个…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
