VIF原理
文章目录
- 一、VIF公式和原理
- 对于R方
- 一般回归模型
- 皮尔逊相关系数中的方差
VIF原理:
一、VIF公式和原理
所谓VIF方法,计算难度并不高。在线性回归方法里,应用最广泛的就是最小二乘法(OLS),只不过我们对每个因子,用其他N个因子进行回归解释。(n+1自变量)
其中有一个检验模型解释能力的检验统计指标为R2(样本可决系数),R2的大小决定了解释变量对因变量的解释能力。而为了检验因子之间的线性相关关系,我们可以通过OLS对单一因子和解释因子进行回归,然后如果其R^2较小,说明此因子被其他因子解释程度较低,线性相关程度较低。
注:之所以不使用协方差计算相关性是由于协方差难以应用在多元线性相关情况下。给出VIF计算方法:
VIF=1/(1−R2)VIF = 1/{}(1-R^2) VIF=1/(1−R2)
(实际-平均/估计-实际) 10 5
从上文很容易看出,VIF越高解释变量和因变量之间线性相关性就越强。
(应该是一个偏离的程度)
R方的解释
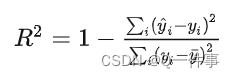
对应上面(10、5)的是,9/10(n变量越能解释1个变量) 4/5(n越大越)----(其他的变量能解释这个变量的90%)
估计-实际/实际-平均
参考:使用方差膨胀因子(Variance Inflation Factor)来特征选择
[1] VIF方法(方差膨胀因子)因子独立性检验 全流程解读
[2] vif: Variance Inflation Factors
[3]Computing Variance Inflation Factor VIF in R Studio
对于R方
一般回归模型
R方是统计学里常用的统计量,在不同任务模型下的解读和用途不一,有时候会出现误用情况。本文总结了对R方的理解和用法,遵循“从一般到特殊”的思路,先讲一般回归模型中的R方,再讲线性回归模型里的R方。"一般"回归模型包括线性模型,随机森林,神经网络等。
- R方的定义
R方的名字是coefficient of determination,另一个名字是Nash–Sutcliffe model efficiency coefficient。给定一系列真值 yi 和对应的预测值y^i,R方的定义为
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CSnx5f5I-1676030637238)(assets/image-20221201205758230.png)]](https://img-blog.csdnimg.cn/51ee490ba69e46ba87eb6a7771d174ee.png)
R方的含义是,预测值解释了 yi 变量的方差的多大比例,衡量的是预测值对于真值的拟合好坏程度。通俗理解,假定 yi 的方差为1个单位,则R方表示"使用该模型之后, yi 的残差的方差减少了多少"。比如R方等于0.8,则使用该模型之后残差的方差为原始 yi 值方差的20%。
- R方=1:最理想情况,所有的预测值等于真值。
- R方=0:一种可能情况是"简单预测所有y值等于y平均值",即所有 y^i 都等于y¯(即真实y值的平均数),但也有其他可能。
- R方<0:模型预测能力差,比"简单预测所有y值等于y平均值"的效果还差。这表示可能用了错误模型,或者模型假设不合理。
- R方的最小值没有下限,因为预测可以任意程度的差。因此,R方的范围是 (−∞,1] 。
- 注意:R方并不是某个数的平方,因此可以是负值。
参考文献:https://zhuanlan.zhihu.com/p/143132259
皮尔逊相关系数中的方差
对于不固定截距的简单线性模型(y = mx + b), R方等于x和y的pearson correlation coefficient的平方。因此,此处的R方范围是[0,1]。R方等于0,表示x和y的散点图完全随机,没有线性关系(或者说,线性相关关系等于0)。R方等于1,表示所有(x,y)散点落在一条直线上。
(ArcGIS Pro How Band Collection Statistics works)
The covariance matrix contains values of variances and covariances. The variance is a statistical measure showing how much variance there is from the mean. To calculate these variances, the squares of the differences between each cell value and the mean value of all cells are averaged. The variances for every layer can be read along the diagonal of the covariance matrix moving from the upper left to the lower right. The variances are expressed in cell-value units squared.
The remaining entries within the covariance matrix are the covariances between all pairs of input rasters. The following formula is used to determine the covariance between layers i and j:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jqG771li-1676030637239)(F:\BaiduSyncdisk\西安生态修复论文\221011分区\assets\GUID-F94265F1-70FD-4FF8-A7AE-9B87BC4EA47D-web.gif)]](https://img-blog.csdnimg.cn/3464e649521341d387456e632c3df602.png)
-
where:
Z - value of a cell
i, j - are layers of a stack
µ - is the mean of a layer
N - is the number of cells
k - denotes a particular cell
The covariance of two layers is the intersection of the appropriate row and column. The covariance between layers 2 and 3 is the same as the covariance between layers 3 and 2. The values of the covariance matrix are dependent on the value units, while the values of the correlation matrix are not.
The correlation matrix shows the values of the correlation coefficients that depict the relationship between two datasets. In the case of a set of raster layers, the correlation matrix presents the cell values from one raster layer as they relate to the cell values of another layer. The correlation between two layers is a measure of dependency between the layers. It is the ratio of the covariance between the two layers divided by the product of their standard deviations. Because it is a ratio, it is a unitless number. The equation to calculate the correlation is as follows:
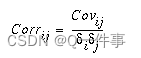
Correlation ranges from +1 to -1. A positive correlation indicates a direct relationship between two layers, such as when the cell values of one layer increase, the cell values of another layer are also likely to increase. A negative correlation means that one variable changes inversely to the other. A correlation of zero means that two layers are independent of one another.
The correlation matrix is symmetrical. Its diagonal from the upper left to lower right is 1.0000 since the correlation coefficient of identical layers is +1.(参考文献:)
这里的R方
R 平方,也称为决定系数,是一种统计量度,表示可从自变量预测的因变量方差的比例。 它是一个介于 0 到 1 之间的数字,用于评估回归模型的拟合优度。 在 Pearson 系数的背景下,R 平方提供了对两个变量之间线性关系强度的估计。
值为 0 表示模型没有解释因变量的任何变化,值为 1 表示模型完美地解释了因变量的变化。 R 平方的中间值表示因变量中由自变量解释的方差的比例。
总之,Pearson 系数的 R 平方值提供了有关回归模型对数据的拟合程度以及变量之间线性关系强度的信息。
参考文献:https://zhuanlan.zhihu.com/p/143132259
总之,Pearson 系数的 R 平方值提供了有关回归模型对数据的拟合程度以及变量之间线性关系强度的信息。
参考文献:https://zhuanlan.zhihu.com/p/143132259
相关文章:
VIF原理
文章目录一、VIF公式和原理对于R方一般回归模型皮尔逊相关系数中的方差VIF原理:一、VIF公式和原理 所谓VIF方法,计算难度并不高。在线性回归方法里,应用最广泛的就是最小二乘法(OLS),只不过我们对每个因子…...

nginx相关反爬策略总结笔记
引言 互联网站点的流量一部分由人类正常访问行为产生,而高达30%-60%的流量则是由网络爬虫产生的,其中一部分包含友好网络爬虫,如搜索引擎的爬虫、广告程序、第三方合作伙伴程序、Robots协议友好程序等;而并非所有的网络爬虫都是友好的&#x…...

【Vue3】电商网站吸顶功能
头部分类导航-吸顶功能 电商网站的首页内容会比较多,页面比较长,为了能让用户在滚动浏览内容的过程中都能够快速的切换到其它分类。需要分类导航一直可见,所以需要一个吸顶导航的效果。 目标:完成头部组件吸顶效果的实现 交互要求 滚动距离大…...

HOMER docker版本安装详细流程
概述 HOMER是一款100%开源的针对SIP/VOIP/RTC的抓包工具和监控工具。 HOMER是一款强大的、运营商级、可扩展的数据包和事件捕获系统,是基于HEP/EEP协议的VoIP/RTC监控应用程序,并可以使用即时搜索、处理和存储大量的信令、RTC事件、日志和统计信息。 …...
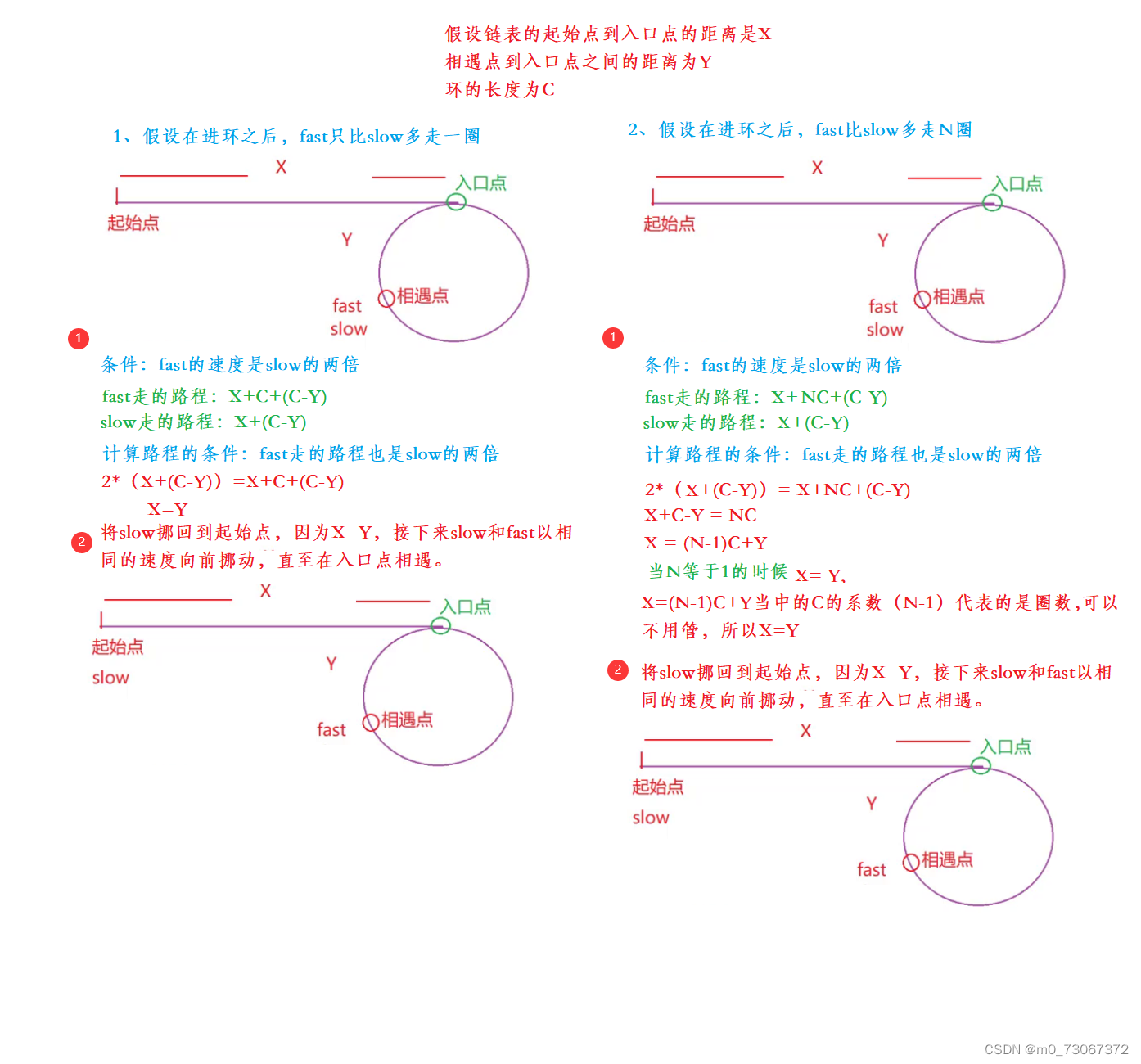
【数据结构】单向链表的练习题
目录 前言 1、删除链表中等于给定值val的所有节点。 【题目描述】 【代码示例】 【 画图理解】 2、反转一个点链表 【题目描述】 【 代码思路】 【代码示例】 【画图理解】 3、给定一个带有头节点head的非空单链表,返回链表的中间节点,如果有两个…...
我的企业需要一个网站吗?答案是肯定的 10 个理由
如果您的企业在没有网站的情况下走到了这一步,您可能会想:我的企业需要一个网站吗?如果我的企业没有一个就已经成功了,那又有什么意义呢?简短的回答是,现在是为您的企业投资网站的最佳或更重要的时机。网站…...
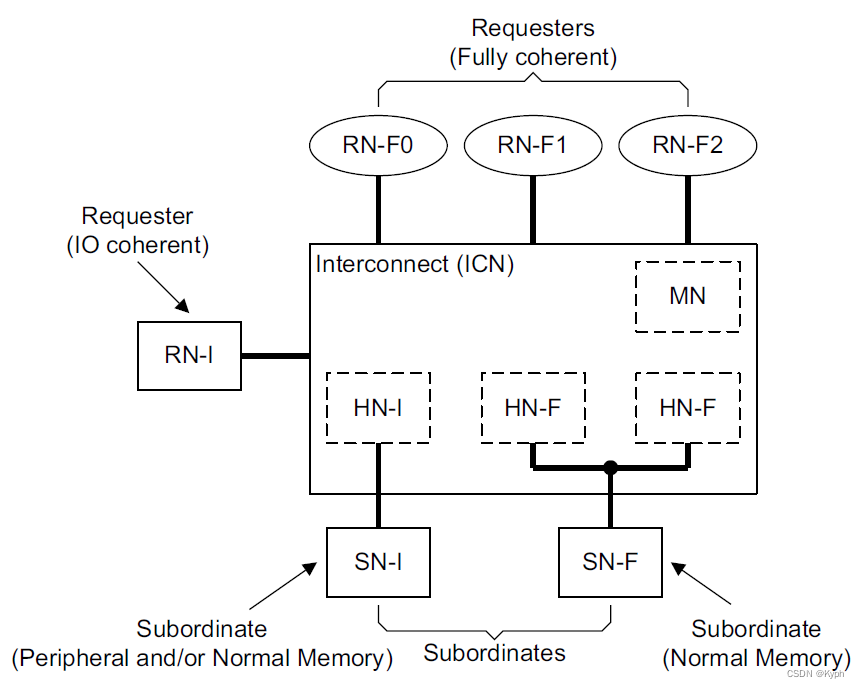
CHI协议定义的NOC组件
请求结点RN 可以向NOC发送读/写等请求事务,有以下几种类型的RN: RN-F 一般是处理器核或者核簇结点,包含了局部cache和一致性部件snoopee。与NOC上的一致性部件一起,维护“可缓存”数据的一致性(这种可缓存数据…...
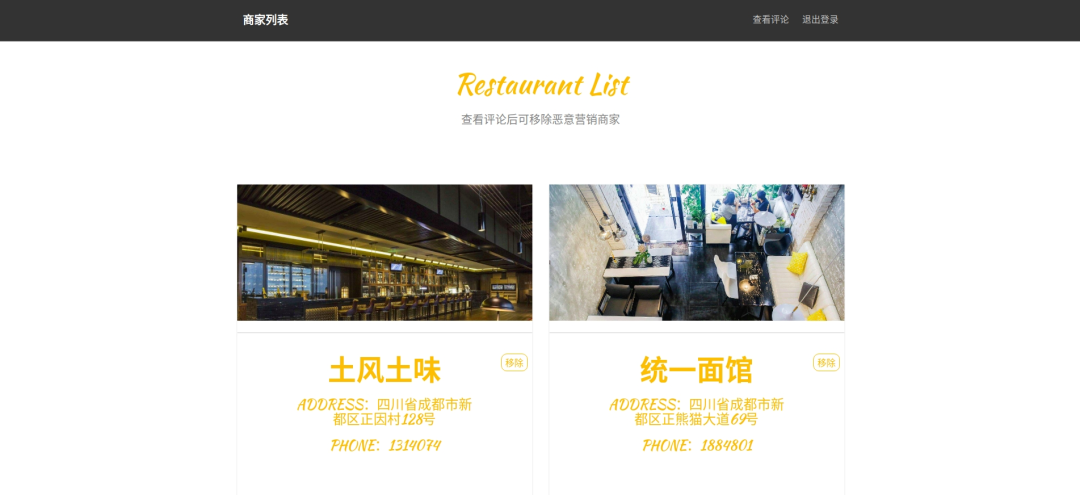
Python+Flask+MySQL开发的在线外卖订餐系统(附源码)
文章目录一、项目模块及功能介绍1、登录模块2、注册模块3、商家用户模块4、买家用户模块5、系统管理员模块源码二、项目结构三、环境依赖四、运行方法五、系统部分界面展示1、首页2、注册界面3、登录界面4、商家主界面5、商家菜单界面6、商家添加菜品界面7、商家修改菜品界面8、…...
 | 部署Placement)
OpenStack云平台搭建(4) | 部署Placement
目录 安装部署Placement 1、登录数据库授权 2、安装palcement-api 安装部署Placement 【Placement】服务 是从【nova】服务中拆分出来的组件,作用是收集各个【node】节点的可用资源,把【node】节点的资源统计写入到【MySQL】【Placement】服务会被【n…...

GNN图神经网络原理解析
一、GNN基本概念 1. 图的基本组成 图神经网络的核心就是进行图模型搭建,图是由点和边组成的。在计算机处理时,通常将数据以向量的形式进行存储。因此,在存储图时,就会有点的向量,点与点之间边的向量,全局向量(描述整张图),邻接矩阵(记录哪些点之间存在关联)等。 既…...

BI-SQL丨ALL、ANY、SOME
ALL、ANY、SOME ALL、ANY和SOME,这三个关键字,在SQL中使用频率较高,通常可以用来进行数据比较筛选。 注:SQL中ALL的用法和DAX中ALL的用法是完全不同的,小伙伴不要混淆了。 那么三者之间的区别是什么呢? A…...

从0到0.1学习 maven(三:声明周期、插件、聚合与继承)
该文章为maven系列学习的第三篇,也是最后一篇 第一篇快速入口:从0到0.1学习 maven(一:概述及简单入门) 第二篇快速入口:从0到0.1学习 maven(二:坐标、依赖和仓库) 文章目录啥子叫生命周期生命周期详解clean生命周期def…...

【直击招聘C++】2.5 this指针
2.5 this指针一、要点归纳1.什么是this指针2.this指针的深入讨论程序1程序23.类成员函数返回对象和返回对象引用的区别二、面试真题解析面试题1面试题2一、要点归纳 1.什么是this指针 this指针是隐含于每一个类对象的特殊指针,该指针值是一个正在被某个成员函数操作…...

spark数据清洗练习
文章目录准备工作删除缺失值 > 3 的数据删除星级、评论数、评分中任意字段为空的数据删除非法数据hotel_data.csv通过编写Spark程序清洗酒店数据里的缺失数据、非法数据、重复数据准备工作 搭建 hadoop 伪分布或 hadoop 完全分布上传 hotal_data.csv 文件到 hadoopidea 配置…...

Android 12首次开机启动Launcher前黑屏问题解析
在工作中,对于系统开发确实有些难度,特别是在开机阶段遇到的问题,比如开机动画播放完毕进入锁屏界面黑屏几秒然后进入 锁屏界面,这就需要根据开机日志来分析问题所在,在工作中遇到的几种黑屏情况做下记录首次开机进入L…...
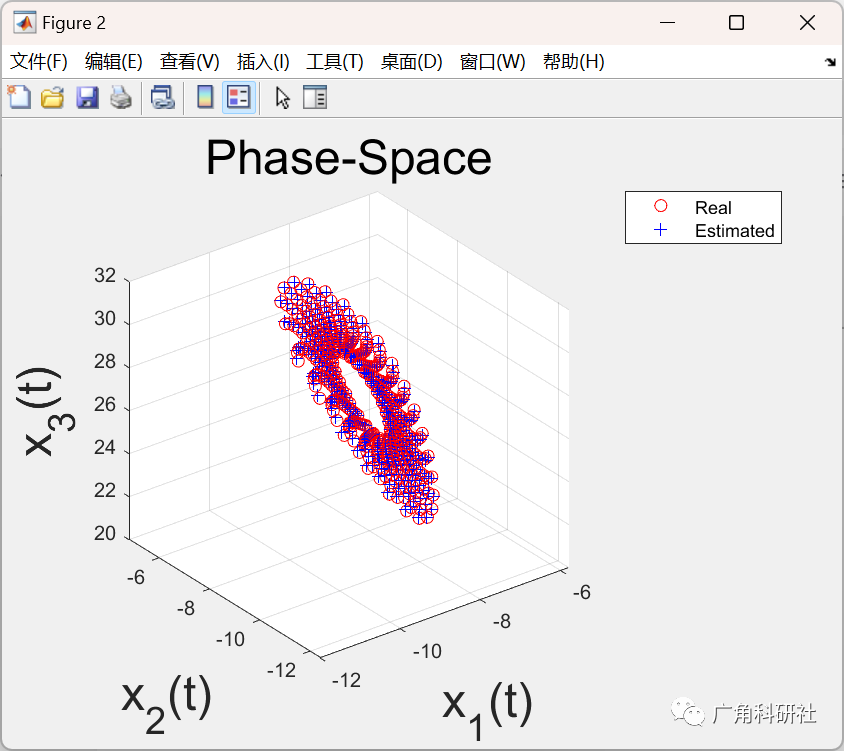
使用 LSSVM 的 Matlab 演示求解反常微分方程问题(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 LSSVM的特性 1) 同样是对原始对偶问题进行求解,但是通过求解一个线性方程组(优化目标中的线性约束导致…...
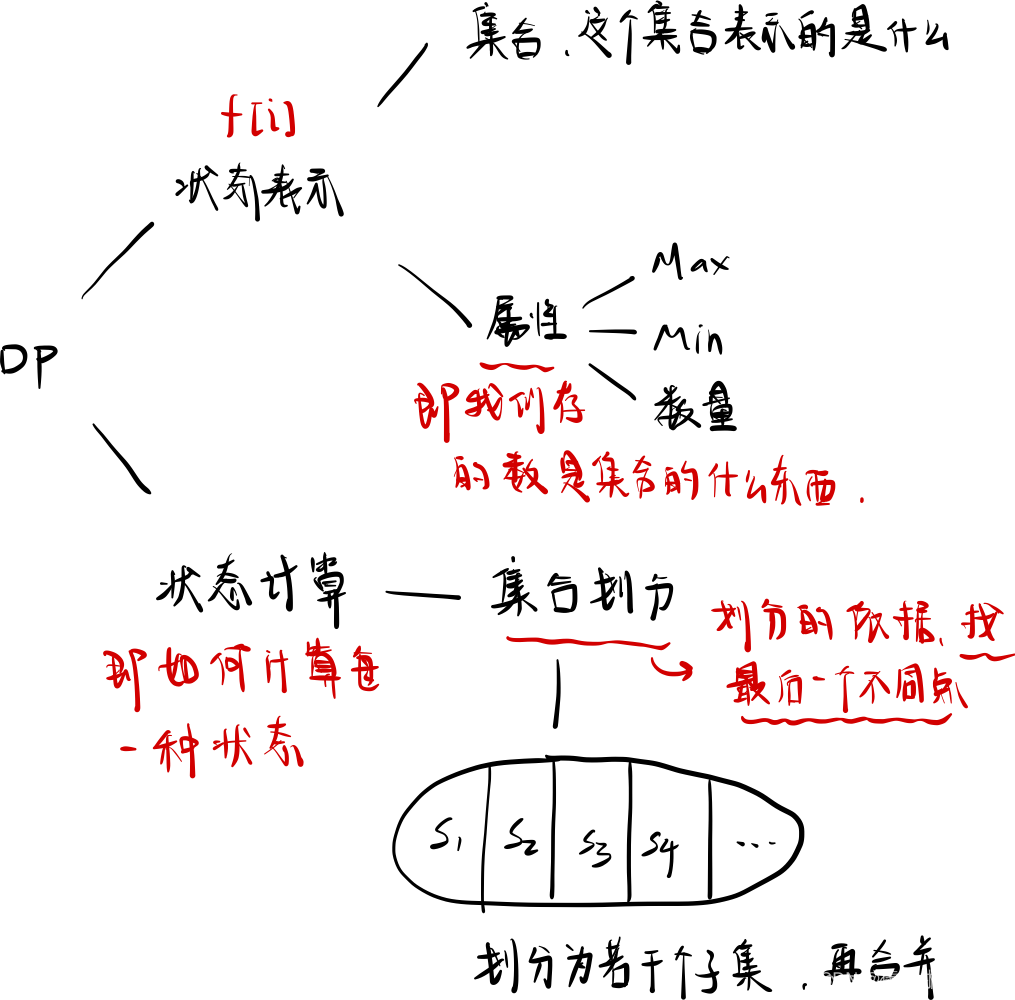
动态规划-背包问题
文章目录一、背包问题1. 背包问题简介2. 背包问题解决方法二、01 背包问题1. 实现思路2. 实现代码三、完全背包问题1. 实现思路2. 实现代码四、多重背包问题(一)1. 实现思路2. 实现代码五、多重背包问题(二)1. 实现思路2. 实现代码…...

计算24点与运算符重载
十几年前写过一个算24点的程序。记得当时有点费劲,不过最后总算捣鼓出来了。前几天突然想再写一次,结果轻松地写出来了。C,总行数不多,带命令行界面和注释共200行不到;利用了面向对象和运算符重载来简化代码。 首先谈…...

MES系统智能工厂,搭上中国制造2025顺风车
MES在电子制造业中的应用日益广泛,越来越多的厂商已经购置或自行开发了MES,并将其作为“智能化工厂”。国内大大小小、各行各业都有上百个MES系统,还有很多的国外MES系统,怎么才能在MES系统公司中找到适合自己的MES?希…...
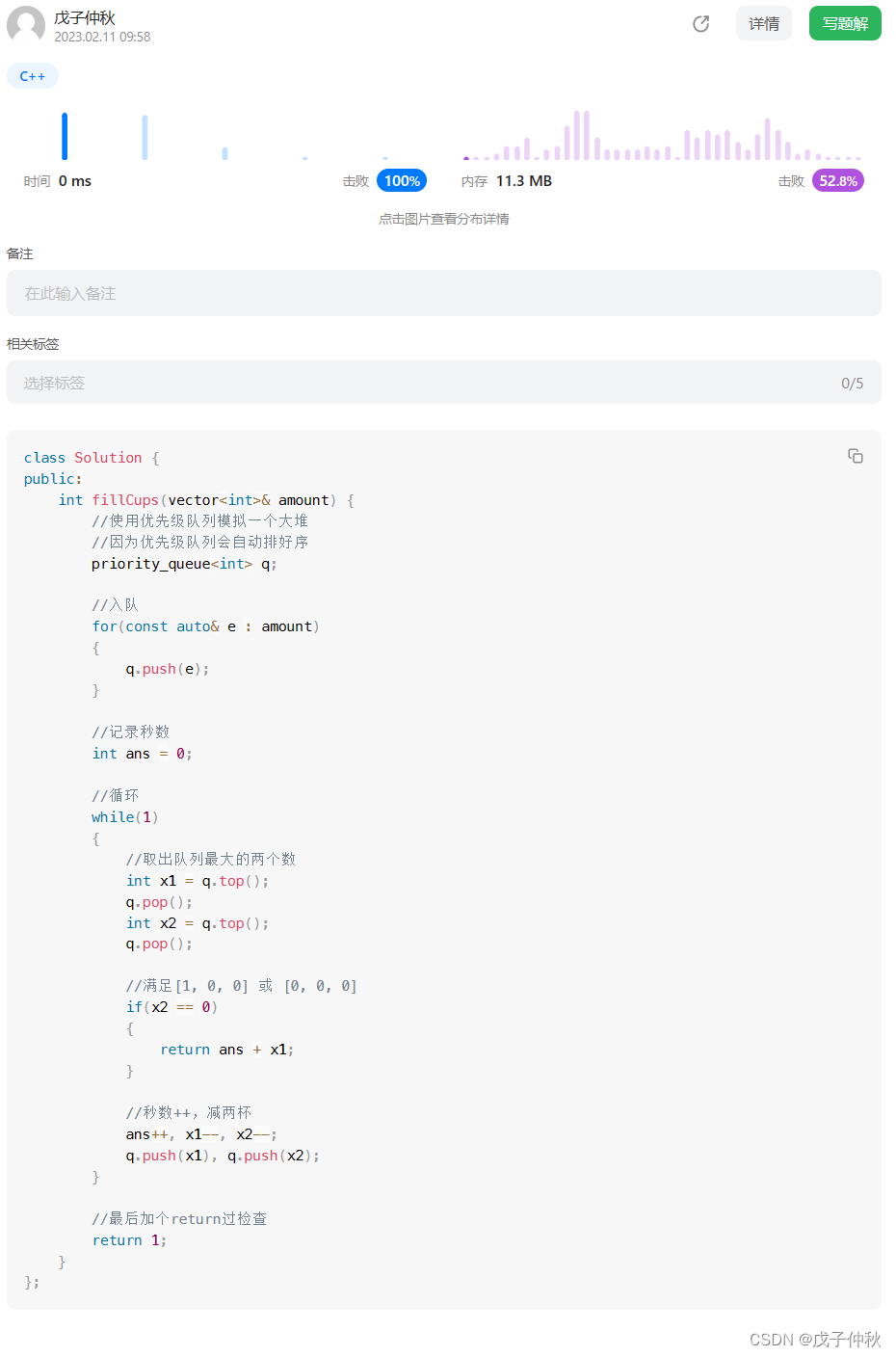
【LeetCode】每日一题(1)
目录 题目: 解题思路: 代码: 写在最后: 题目: 这是他给出的接口: class Solution { public:int fillCups(vector<int>& amount) {} }; 作为一个数学学渣,我想不出厉害的数学算法…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
