动态规划-背包问题
文章目录
- 一、背包问题
- 1. 背包问题简介
- 2. 背包问题解决方法
- 二、01 背包问题
- 1. 实现思路
- 2. 实现代码
- 三、完全背包问题
- 1. 实现思路
- 2. 实现代码
- 四、多重背包问题(一)
- 1. 实现思路
- 2. 实现代码
- 五、多重背包问题(二)
- 1. 实现思路
- 2. 实现代码
- 六、分组背包问题
- 1. 实现思路
- 2. 实现代码
一、背包问题
1. 背包问题简介
- 背包问题可以理解为,给定一个背包容量 target,再给定一个数组 nums(用以表示物品),能否按一定方式选取 nums 中的元素得到 target。
- 这里需要注意的有以下几点:
- (1) 背包容量 target 和物品 nums 的类型可能是数,也可能是字符串。
- (2) target 可能题目已经给出(显式),也可能是需要我们从题目的信息中挖掘出来(非显式)(常见的非显式 target 比如 sum/2 等)。
- (3) 选取方式有常见的一下几种:每个元素选一次/每个元素选多次/选元素进行排列组合 那么对应的背包问题就是下面我们要讲的背包分类。
- 背包问题主要可以分为四类,分别是:01 背包问题,完全背包问题,多重背包问题和分组背包问题。
- (1) 01 背包问题
- 01 背包问题是一种非常经典的背包问题。
- 01 背包问题主要是给定一个背包容量 VVV,再给定 NNN 件物品,每个物品有两种属性,分别是体积 viv_ivi 和价值(权重) wiw_iwi,每件物品最多可以使用一次(即不是 0 次就是 1 次两种选择)。
- 问题是要在背包能装下的情况下,所挑出的物品总价值最大。
- (2) 完全背包问题
- 完全背包问题每件物品有无限个,只要背包的体积够用,就可以无限装同一个物品。
- (3) 多重背包问题
- 每个物品最多有 sis_isi 个,包含一个朴素版和优化版。
- (4) 分组背包问题
- 有 NNN 组物品,每一组物品有若干个,每组物品当中只可以选一个,在此限制条件下求物品的最大价值。
- 上述的四种问题都是在背包体积足够的情况下,求解所能容纳物品的最大价值,这里需要注意的是,背包不一定非要装满。
2. 背包问题解决方法
- 对于上述问题,我们常使用动态规划解决此类问题。
- 动态规划总共包括两大部分,分别是状态表示(判断是几维,两维就是 f(i,j)f(i,j)f(i,j),每一个状态的含义是什么)和状态计算(如何计算出每一个 f(i,j)f(i,j)f(i,j))。
- 动态规划的优化通常都是对代码或者计算方程进行等价变化。
- f(i,j)f(i,j)f(i,j) 表示的选择方法只指从前 iii 个物品中选和总体积不超过 jjj。
- 状态表示可分为集合(每一个状态表示的都是一个集合)和属性(包括最大值,最小值,元素的数量,我们的背包问题就是属性当中的最大值)。
- 状态计算对应的是集合的划分(每一个元素当前只会属于一个集合,每一个元素都存在),将 f(i,j)f(i,j)f(i,j) 划分为若干个子集和,每一个子集合都可以由更小的子集合表示。
二、01 背包问题
题目描述
有 NNN 件物品和一个容量是 VVV 的背包。每件物品只能使用一次。
第 iii 件物品的体积是 viv_ivi,价值是 wiw_iwi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,NNN,VVV,用空格隔开,分别表示物品数量和背包容积。
接下来有 NNN 行,每行两个整数 vi,wiv_i,w_ivi,wi,用空格隔开,分别表示第 iii 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤10000<N,V≤10000<N,V≤1000
0<vi,wi≤10000<v_i,w_i≤10000<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
8
具体实现
1. 实现思路
- 01 背包问题的集合划分是一种非常经典的划分方法,可整体划分为两部分,不包含 iii 和包含 iii。
- 不包含 iii 可以理解为,从 1到i−11到i-11到i−1 当中选取物品,总体积不大于 jjj,该集合的最大值就是 f(i−1,j)f(i-1,j)f(i−1,j)。
- 包含 iii 可以理解为,从 1到i1到i1到i 当中选取物品,总体积不大于 jjj,该集合的最大值直接求取的困难很大,我们可以曲线救国,先将所有选法当中的第 iii 个物品去掉(最大的那部分是依旧是最大的),便转换为从 1到i−11到i-11到i−1 当中选取物品,总体积不大于 j−vij-v_ij−vi,此时所有选法的最大值就是 f(i−1,j−vi)f(i-1,j-v_i)f(i−1,j−vi),但由于我们去掉过第 iii 个物品,因此,原本的最大值就是 f(i−1,j−vi)+wif(i-1,j-v_i)+w_if(i−1,j−vi)+wi。
- 那么,最后所有的最大值就是 max(f(i−1,j),f(i−1,j−vi)+wi)max(f(i-1,j),f(i-1,j-v_i)+w_i)max(f(i−1,j),f(i−1,j−vi)+wi)。
- 上述采用的是二维实现方法,对此,可以使用滚动数组将二维降阶为一维。
2. 实现代码
#include <bits/stdc++.h>using namespace std;const int N = 1010;//n, m表示物品种数和背包体积
int n, m;
//v[N], w[N]表示物品的体积和价值
int v[N], w[N];
//f[N][N]表示总价值
int f[N][N];int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ){cin >> v[i] >> w[i];}//二维实现方法for (int i = 1; i <= n; i ++ ){for (int j = 0; j <= m; j ++ ){f[i][j] = f[i - 1][j];if (j >= v[i]) //如果可以装下当前第i个物品{f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);}}} cout << f[n][m] << endl;return 0;
}
三、完全背包问题
题目描述
有 NNN 种物品和一个容量是 VVV 的背包,每种物品都有无限件可用。
第 iii 种物品的体积是 viv_ivi,价值是 wiw_iwi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,NNN,VVV,用空格隔开,分别表示物品种数和背包容积。
接下来有 NNN 行,每行两个整数 vi,wiv_i,w_ivi,wi,用空格隔开,分别表示第 iii 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤10000<N,V≤10000<N,V≤1000
0<vi,wi≤10000<v_i,w_i≤10000<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
10
具体实现
1. 实现思路
- 完全背包问题和 01 背包问题的区别在于完全背包问题当中的物品可以被选择无数次。
- 完全背包问题可以选择使用一维或二维进行解决,如果直接使用与 01 背包问题相同的方法是三个 for 循环,此时会超时,就需要进行优化。
- 那么,f[i]f[i]f[i] 就表示体积是 iii 的情况下,最大价值是多少(状态表示)。
- f[0……m]f[0……m]f[0……m] 当中的最大值就是我们所求的结果。
2. 实现代码
#include <bits/stdc++.h>using namespace std;const int N = 1010;//n, m表示物品数量和背包体积
int n, m;
//v[N], w[N]表示物品的体积和价值
int v[N], w[N];
//f[N]表示总价值
int f[N];int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ){cin >> v[i] >> w[i];}for (int i = 1; i <= n; i ++ ){for (int j = v[i]; j <= m; j ++ ){f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[m] << endl;return 0;
}
四、多重背包问题(一)
题目描述
有 NNN 种物品和一个容量是 VVV 的背包。
第 iii 种物品最多有 sis_isi 件,每件体积是 viv_ivi,价值是 wiw_iwi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,NNN,VVV,用空格隔开,分别表示物品种数和背包容积。
接下来有 NNN 行,每行三个整数 vi,wi,siv_i,w_i,s_ivi,wi,si,用空格隔开,分别表示第 iii 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000<N,V≤1000<N,V≤100
0<vi,wi,si≤1000<v_{i},w_{i},s_{i}≤1000<vi,wi,si≤100
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例
10
具体实现
1. 实现思路
- 多重背包问题与上述两种背包问题的区别在于每个物品最多有 sis_isi 个。
- 此题与 01 背包问题基本相同。
2. 实现代码
#include <bits/stdc++.h>using namespace std;const int N = 110;//n, m表示物品种数和背包体积
int n, m;
//v[N], w[N],s[N]表示物品的体积,价值,数量
int v[N], w[N], s[N];
//f[N][N]表示价值
int f[N][N];int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ){cin >> v[i] >> w[i] >> s[i];}for (int i = 1; i <= n; i ++ ){for (int j = 0; j <= m; j ++ ){for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ ){f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);}}}cout << f[n][m] << endl;return 0;
}
五、多重背包问题(二)
题目描述
有 NNN 种物品和一个容量是 VVV 的背包。
第 iii 种物品最多有 sis_isi 件,每件体积是 viv_ivi,价值是 wiw_iwi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,NNN,VVV,用空格隔开,分别表示物品种数和背包容积。
接下来有 NNN 行,每行三个整数 vi,wi,siv_i,w_i,s_ivi,wi,si,用空格隔开,分别表示第 iii 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N≤10000<N≤10000<N≤1000
0<V≤20000<V≤20000<V≤2000
0<vi,wi,si≤20000<v_{i},w_{i},s_{i}≤20000<vi,wi,si≤2000
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例
10
具体实现
1. 实现思路
- 多重背包问题(二)与多重背包问题(一)的区别在于(二)的数据范围进行了扩大,如果直接暴力做法会导致超时,因此,需要进行优化。
- 由于(一)当中的做法与 01 背包问题基本相同,所以,我们只需要对与 01 背包问题相同的那一段进行优化。
- 这里引入二进制优化方法(用二进制表示十进制)。
- 举例说明,如果我们要从 0 枚举到 1023,十进制的做法需要我们枚举 1023 次,如果采用二进制做法,我们需要将 1023 分成十组,分别是 1,2,4,8,16,32,64,128,256 和 512,我们在这十组数字当中,每组任意取出一个数字,组合起来就可以得到 0 到1023 当中的任何数字,此时,我们只需要枚举 10 次即可。
2. 实现代码
#include <bits/stdc++.h>using namespace std;const int N = 12010, M = 2010;//n,m表示物品种数和背包容积
int n, m;
//v[N], w[N]表示每组物品的总体积和总价值
int v[N], w[N];
//f[M]表示价值
int f[M];int main()
{cin >> n >> m;//二进制枚举int cnt = 0;//将物品重新分组后的顺序for (int i = 1; i <= n; i ++ ){//a, b, s表示是每种物品的体积、价值和数量。int a, b, s;cin >> a >> b >> s;int k = 1; //二进制拆分,打包时每组中有 k 个同种物品while (k <= s) //最后一组的物品个数 < 2^(n+1) 1 2 4 8 16 ... 2^n 2^(n+1){cnt ++ ;v[cnt] = a * k;// 每组的体积w[cnt] = b * k;// 每组的价值s -= k; //得到剩余的物品数量k *= 2;// 注意是 k * 2,每次增长一倍,不是k * k}if (s > 0)// 二进制拆分完之后 剩下的物品个数分为新的一组{cnt ++ ;v[cnt] = a * s;w[cnt] = b * s;}}n = cnt; //将所得组数赋值给物品种数for (int i = 1; i <= n; i ++ ){for (int j = m; j >= v[i]; j -- ){f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[m] << endl;return 0;
}
六、分组背包问题
题目描述
有 NNN 组物品和一个容量是 VVV 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 vijv_{ij}vij,价值是 wijw_{ij}wij,其中 iii 是组号,jjj 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 NNN,VVV,用空格隔开,分别表示物品组数和背包容量。
接下来有 NNN 组数据:
- 每组数据第一行有一个整数 SiS_iSi,表示第 iii 个物品组的物品数量;
- 每组数据接下来有 SiS_iSi 行,每行有两个整数 vij,wijv_{ij},w_{ij}vij,wij,用空格隔开,分别表示第 iii 个物品组的第 jjj 个物品的体积和价值;
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000<N,V≤1000<N,V≤100
0<Si≤1000<Si≤1000<Si≤100
0<vij,wij≤1000<v_{ij},w_{ij}≤1000<vij,wij≤100
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例
8
具体实现
1. 实现思路
- 分组背包问题是指我们有 NNN 组物品,每组物品当中有若干个物品,每个物品的体积和价值各有不同,每组物品当中最多只能选一个(可以不选)。
2. 实现代码
#include <bits/stdc++.h>using namespace std;const int N = 110;//n,m表示物品组数和背包容积
int n, m;
//v[N][N], w[N][N], s[N]表示物品的体积,价值和数量
int v[N][N], w[N][N], s[N];
//f[N]表示总价值
int f[N];int main()
{cin >> n >> m;//每组物品的数据进行读入for (int i = 1; i <= n; i ++ ){cin >> s[i];for (int j = 1; j < s[i]; j ++ ){cin >> v[i][j] >> w[i][j];}}for (int i = 1; i <= n; i ++ ){for (int j = m; j >= 0; j -- ){for (int k = 0; k < s[i]; k ++ ){if (v[i][k] <= j){f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);}}}}cout << f[m] << endl;return 0;
}
相关文章:

动态规划-背包问题
文章目录一、背包问题1. 背包问题简介2. 背包问题解决方法二、01 背包问题1. 实现思路2. 实现代码三、完全背包问题1. 实现思路2. 实现代码四、多重背包问题(一)1. 实现思路2. 实现代码五、多重背包问题(二)1. 实现思路2. 实现代码…...

计算24点与运算符重载
十几年前写过一个算24点的程序。记得当时有点费劲,不过最后总算捣鼓出来了。前几天突然想再写一次,结果轻松地写出来了。C,总行数不多,带命令行界面和注释共200行不到;利用了面向对象和运算符重载来简化代码。 首先谈…...

MES系统智能工厂,搭上中国制造2025顺风车
MES在电子制造业中的应用日益广泛,越来越多的厂商已经购置或自行开发了MES,并将其作为“智能化工厂”。国内大大小小、各行各业都有上百个MES系统,还有很多的国外MES系统,怎么才能在MES系统公司中找到适合自己的MES?希…...
【LeetCode】每日一题(1)
目录 题目: 解题思路: 代码: 写在最后: 题目: 这是他给出的接口: class Solution { public:int fillCups(vector<int>& amount) {} }; 作为一个数学学渣,我想不出厉害的数学算法…...
SpringCloud-Netflix学习笔记11——Hystrix实现服务降级
服务降级 是什么? 整体资源快不够了,忍痛将某些服务先关掉,待渡过难关,再开启回来。 如下图,在某一个时间段,访问服务A的请求特别多,而访问服务B和服务C的请求特别少,这时我们可以把…...

Oracle Dataguard(主库为 Oracle rac 集群)配置教程(03)—— 创建 dataguard 数据库之前的准备工作
Oracle Dataguard(主库为 Oracle rac 集群)配置教程(03)—— 创建 dataguard 数据库之前的准备工作 / 本专栏详细讲解 Oracle Dataguard(Oracle 版本为11g,主库为双节点 Oracle rac 集群)的配置…...

零代码做分析报表的bi软件才是好软件
有些数据分析软件对IT的依赖比较重,在制作报表的过程中需要用到SQL,这就导致了IT人员懂技术不懂业务,业务人员懂业务不懂技术,数据分析做来做去总是差点什么的局面。要是遇到了IT部门相对较弱的情况,还会加重IT负担&am…...

linux ALSA 驱动架构
一、kernel Audio驱动架构主流有两大类,一类是SOC Machine架构,另一类是simple-card架构。 MTK、QCom主要采用machine架构,rockchip采用simple card架构。 二、Machine架构驱动介绍 machine 架构每家平台实现并不完全相同,mach…...

JDK 8 JVM内存结构详解
前言 本文所介绍的是 JDK 1.8 版本,其他版本的 JDK 在这里并不一定正确;内容主要摘自周志明的《深入理解Java虚拟机》一书的关键点,并根据自身的理解进行记录。感兴趣的同学可以去阅读原著。 JVM 的内存结构,主要包括以下 5 个区…...
黑马程序员 Linux 教程
目录Linux 简介不同应用领域主流操作系统Linux 系统历史Linux 系统版本Linux 安装安装方式网卡设置安装 SSH 连接工具使用 FinalShell 连接到 LinuxLinux 和 Windows 目录结构对比Linux 目录介绍Linux 常用命令Linux 命令初体验Linux 命令使用技巧Linux 命令格式文件目录操作命…...

文件操作 -- IO
文章目录文件操作 -- IO文件 :文件路径 :文件的类型java 中的文件操作文件内容的相关操作字节流的读和写操作字符流的读和写操作代码案例代码案例一 :代码案例二 :代码案例三 :文件操作 – IO 文件 : 文件相比大家都不陌生把 , 打…...

FPGA解析串口协议帧3.0版本,增加了错误重发功能,提供仿真文件以及源码
FPGA解析串口协议帧已经发布2个版本了,分别如下: 版本1:点击查看版本1 版本1详细介绍了串口协议帧的帧组成和设计思想,但设计粗糙,注释不详细; 版本1:点击查看版本2 版本2优化了代码,…...
365天深度学习训练营 第P6周:好莱坞明星识别
🍨 本文为🔗365天深度学习训练营 内部限免文章(版权归 K同学啊 所有)🍦 参考文章地址: 🔗第P6周:好莱坞明星识别 | 365天深度学习训练营🍖 作者:K同学啊 | 接…...

一文读懂 Zebec Chain 的“先行网络” Nautilus 链
最近,Zebec 上线了 DAO 治理系统后,上线并通过了关于 Nautilus 链的提案,这也是DAO系统上线后通过的首个提案。 Nautilus 链可以被看作是Zebec Chain上线前的“先行”链,并且是目前行业内为数不多的以“Layer3”作为特点的模块化通…...

FuzzyMathematicalModel模糊数学模型-2-多目标模糊综合评价案例分享
主函数:clc, clear% 输入模糊矩阵的原型x [4700 6700 5900 8800 76005000 5500 5300 6800 600004.0 06.1 05.5 07.0 06.80030 0050 0040 0200 01601500 0700 1000 0050 0100];r muti_objective_fuzzy_analysis(x);% 各指标在决策中占的权重(专家系统,自…...

单链表--C语言版(从0开始,超详细解析,小白一看就会)
目录 一、前言 🍎 为什么要学习链表 💦顺序表有缺陷 💦 优化方案:链表 二、链表详解 🍐链表的概念 🍉链表的结构组成:节点 🍓链表节点的连接(逻辑结构与物理结构的区…...
)
cv2-特征点匹配(bf、FLANN)
cv2-特征点匹配(bf、KNN、FLANN) 文章目录cv2-特征点匹配(bf、KNN、FLANN)1. 暴力匹配法(bf)1.1 bf.match()1.2 bf.knnMatch()3. FLANN匹配法4. 总结1. 暴力匹配法(bf) (…...
基于matlab多功能相控阵雷达资源管理的服务质量优化
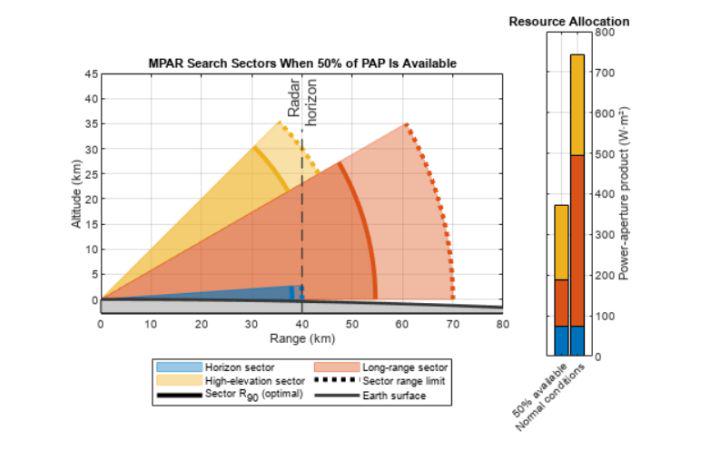
一、前言此示例说明如何为基于服务质量 (QoS) 优化的多功能相控阵雷达 (MPAR) 监控设置资源管理方案。它首先定义必须同时调查的多个搜索扇区的参数。然后,它介绍了累积检测范围作为搜索质量的度量,并展示了…...
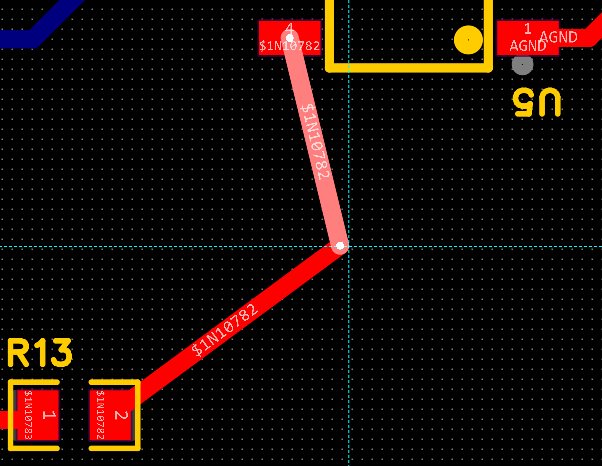
立创eda专业版学习笔记(6)(pcb板移动节点)
先要看一个设置方面的东西: 进入设置-pcb-通用 我鼠标放到竖着的线上面,第一次点左键是这样选中的: 再点一次左键是这样选中的: 这个时候,把鼠标放到转角的地方,点右键,就会出现对于节点的选项…...

Java面试——MyBatis相关知识
目录 1.什么是MyBatis 2.MyBatis优缺点 3.MyBatis工作原理 4.MyBatis缓存模式 5.MyBatis代码相关问题 6.MyBatis和hibernate区别 1.什么是MyBatis MyBatis是一个半ORM持久层框架(对象关系映射),基于JDBC进行封装,使得开发者…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
