使用 LSSVM 的 Matlab 演示求解反常微分方程问题(Matlab代码实现)
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
👨💻4 Matlab代码
💥1 概述
LSSVM的特性
1) 同样是对原始对偶问题进行求解,但是通过求解一个线性方程组(优化目标中的线性约束导致的)来代替SVM中的QP问题(简化求解过程),对于高维输入空间中的分类以及回归任务同样适用;
2) 实质上是求解线性矩阵方程的过程,与高斯过程(Gaussian processes),正则化网络(regularization networks)和费雪判别分析(Fisher discriminant analysis)的核版本相结合;
3) 使用了稀疏近似(用来克服使用该算法时的弊端)与稳健回归(稳健统计);
4) 使用了贝叶斯推断(Bayesian inference);
5) 可以拓展到非监督学习中:核主成分分析(kernel PCA)或密度聚类;
6) 可以拓展到递归神经网络中。
📚2 运行结果

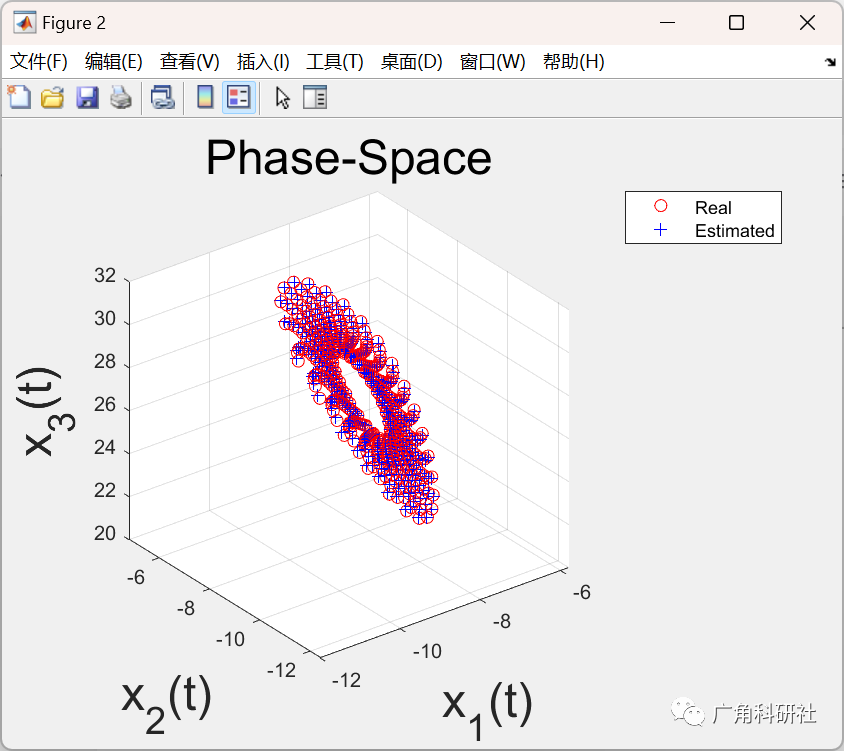
主函数部分代码:
% dot(x1) = a * (x_2 -x_1)
% dot(x_2) = x_1 * (b- x_3) - x_2
% dot(x_3) = x_1 * x_2 -c* x_3
% 0 <= t < = t_f
% Initial Condition
% x_1(0) = -9.42, x_2(0)= -9.34, x_3(0)=28.3
% Theta=[a, b, c] = [10, 28, 8/3]
%% ============================================================================
clear all; close all; clc
t0=0;
tf=10;
sampling_time=0.05;
t=(t0:sampling_time:tf)';
initial=[-9.42 -9.34 28.3]; % initial values of the ODE used for generating simulated data
ExactTheta=[10; 28 ; 8/3]; % The exact parameters of the lorenz system used for generating simulated data
cprintf( [1 0.1 0],'**** Excat parameters of the Lorenz system ***** \n\n');
fprintf('True theta_1= %f \n', ExactTheta(1));
fprintf('True theta_2= %f \n', ExactTheta(2));
fprintf('True theta_3= %f \n\n', ExactTheta(3));
fprintf( '************************************* \n\n');
%% ========= Generating the simulation data ======================
options = odeset('RelTol',1e-5,'AbsTol',[1e-5 1e-5 1e-5]);
sol = ode45(@ridg,[t0 tf],initial,options,ExactTheta);
Y=deval(sol,t);
Y=Y';
noise_level=0.01; % 0.03, 0.05, 0.07, 0.1
noise=noise_level*randn(size(t,1),1);
y1=Y(:,1)+noise;
y2=Y(:,2)+noise;
y3=Y(:,3)+noise;
%% Estimating the parameters of the ODE system:
num_realization =3;
K_fold=3;
num_grid_gam=10;
num_grid_sig=10;
gamma_range = logspace(0,6,num_grid_gam);
sigma_range = logspace(-3,1,num_grid_sig);
ER1=[];
ER2=[];
ER3=[];
Par1=zeros(num_realization,1);
Par2=zeros(num_realization,1);
Par3=zeros(num_realization,1);
BB1=zeros(num_grid_gam,num_grid_sig);
BB2=zeros(num_grid_gam,num_grid_sig);
BB3=zeros(num_grid_gam,num_grid_sig);
for itr=1:num_realization
cprintf( [1 0.1 0],'**** iteration =%d\n',itr);
n=size(t,1);
ind=crossvalind('Kfold', n, K_fold);
for gamma_idx=1:size(gamma_range,2)
gamma = gamma_range(gamma_idx);
for sig_idx=1:size(sigma_range,2)
sig = sigma_range(sig_idx);
test_errors_1=zeros(K_fold,1);
test_errors_2=zeros(K_fold,1);
test_errors_3=zeros(K_fold,1);
for i=1:K_fold
Xte=t(ind==i,1);
Yte_1=y1(ind==i,1);
Yte_2=y2(ind==i,1);
Yte_3=y3(ind==i,1);
Xtr=t(ind~=i,1);
Ytr_1=y1(ind~=i,1);
Ytr_2=y2(ind~=i,1);
Ytr_3=y3(ind~=i,1);
K=KernelMatrix(Xtr,'RBF_kernel', sig);
m=size(K,1);
A= [K + (1/gamma) * eye(m), ones(m,1);...
ones(m,1)' ,0];
B1= [Ytr_1;0];
B2= [Ytr_2;0];
B3= [Ytr_3;0];
result1=A\B1;
result2=A\B2;
result3=A\B3;
alpha1=result1(1:m);
b1=result1(end);
alpha2=result2(1:m);
b2=result2(end);
alpha3=result3(1:m);
b3=result3(end);
yhattr1 = K * alpha1 + b1;
yhattr2 = K * alpha2 + b2;
yhattr3 = K * alpha3 + b3;
🎉3 参考文献
[1]姜星宇. 基于动态粒子群算法的DPSO-LSSVM模型在短期电力负荷预测中的应用研究[D].沈阳农业大学,2022.DOI:10.27327/d.cnki.gshnu.2022.000596.
👨💻4 Matlab代码
相关文章:

使用 LSSVM 的 Matlab 演示求解反常微分方程问题(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 LSSVM的特性 1) 同样是对原始对偶问题进行求解,但是通过求解一个线性方程组(优化目标中的线性约束导致…...
动态规划-背包问题
文章目录一、背包问题1. 背包问题简介2. 背包问题解决方法二、01 背包问题1. 实现思路2. 实现代码三、完全背包问题1. 实现思路2. 实现代码四、多重背包问题(一)1. 实现思路2. 实现代码五、多重背包问题(二)1. 实现思路2. 实现代码…...

计算24点与运算符重载
十几年前写过一个算24点的程序。记得当时有点费劲,不过最后总算捣鼓出来了。前几天突然想再写一次,结果轻松地写出来了。C,总行数不多,带命令行界面和注释共200行不到;利用了面向对象和运算符重载来简化代码。 首先谈…...

MES系统智能工厂,搭上中国制造2025顺风车
MES在电子制造业中的应用日益广泛,越来越多的厂商已经购置或自行开发了MES,并将其作为“智能化工厂”。国内大大小小、各行各业都有上百个MES系统,还有很多的国外MES系统,怎么才能在MES系统公司中找到适合自己的MES?希…...
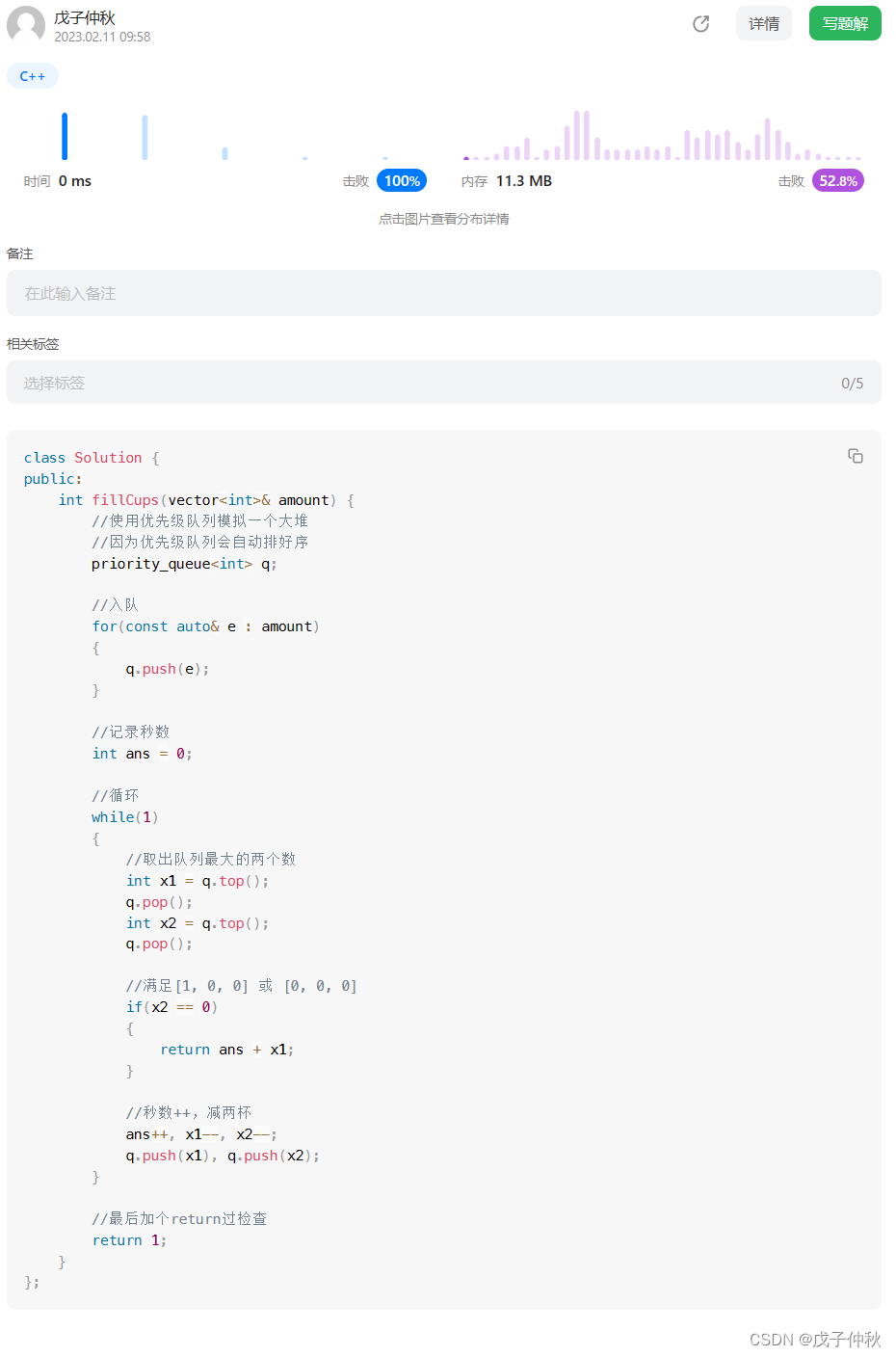
【LeetCode】每日一题(1)
目录 题目: 解题思路: 代码: 写在最后: 题目: 这是他给出的接口: class Solution { public:int fillCups(vector<int>& amount) {} }; 作为一个数学学渣,我想不出厉害的数学算法…...
SpringCloud-Netflix学习笔记11——Hystrix实现服务降级
服务降级 是什么? 整体资源快不够了,忍痛将某些服务先关掉,待渡过难关,再开启回来。 如下图,在某一个时间段,访问服务A的请求特别多,而访问服务B和服务C的请求特别少,这时我们可以把…...

Oracle Dataguard(主库为 Oracle rac 集群)配置教程(03)—— 创建 dataguard 数据库之前的准备工作
Oracle Dataguard(主库为 Oracle rac 集群)配置教程(03)—— 创建 dataguard 数据库之前的准备工作 / 本专栏详细讲解 Oracle Dataguard(Oracle 版本为11g,主库为双节点 Oracle rac 集群)的配置…...

零代码做分析报表的bi软件才是好软件
有些数据分析软件对IT的依赖比较重,在制作报表的过程中需要用到SQL,这就导致了IT人员懂技术不懂业务,业务人员懂业务不懂技术,数据分析做来做去总是差点什么的局面。要是遇到了IT部门相对较弱的情况,还会加重IT负担&am…...

linux ALSA 驱动架构
一、kernel Audio驱动架构主流有两大类,一类是SOC Machine架构,另一类是simple-card架构。 MTK、QCom主要采用machine架构,rockchip采用simple card架构。 二、Machine架构驱动介绍 machine 架构每家平台实现并不完全相同,mach…...

JDK 8 JVM内存结构详解
前言 本文所介绍的是 JDK 1.8 版本,其他版本的 JDK 在这里并不一定正确;内容主要摘自周志明的《深入理解Java虚拟机》一书的关键点,并根据自身的理解进行记录。感兴趣的同学可以去阅读原著。 JVM 的内存结构,主要包括以下 5 个区…...
黑马程序员 Linux 教程
目录Linux 简介不同应用领域主流操作系统Linux 系统历史Linux 系统版本Linux 安装安装方式网卡设置安装 SSH 连接工具使用 FinalShell 连接到 LinuxLinux 和 Windows 目录结构对比Linux 目录介绍Linux 常用命令Linux 命令初体验Linux 命令使用技巧Linux 命令格式文件目录操作命…...

文件操作 -- IO
文章目录文件操作 -- IO文件 :文件路径 :文件的类型java 中的文件操作文件内容的相关操作字节流的读和写操作字符流的读和写操作代码案例代码案例一 :代码案例二 :代码案例三 :文件操作 – IO 文件 : 文件相比大家都不陌生把 , 打…...

FPGA解析串口协议帧3.0版本,增加了错误重发功能,提供仿真文件以及源码
FPGA解析串口协议帧已经发布2个版本了,分别如下: 版本1:点击查看版本1 版本1详细介绍了串口协议帧的帧组成和设计思想,但设计粗糙,注释不详细; 版本1:点击查看版本2 版本2优化了代码,…...
365天深度学习训练营 第P6周:好莱坞明星识别
🍨 本文为🔗365天深度学习训练营 内部限免文章(版权归 K同学啊 所有)🍦 参考文章地址: 🔗第P6周:好莱坞明星识别 | 365天深度学习训练营🍖 作者:K同学啊 | 接…...

一文读懂 Zebec Chain 的“先行网络” Nautilus 链
最近,Zebec 上线了 DAO 治理系统后,上线并通过了关于 Nautilus 链的提案,这也是DAO系统上线后通过的首个提案。 Nautilus 链可以被看作是Zebec Chain上线前的“先行”链,并且是目前行业内为数不多的以“Layer3”作为特点的模块化通…...

FuzzyMathematicalModel模糊数学模型-2-多目标模糊综合评价案例分享
主函数:clc, clear% 输入模糊矩阵的原型x [4700 6700 5900 8800 76005000 5500 5300 6800 600004.0 06.1 05.5 07.0 06.80030 0050 0040 0200 01601500 0700 1000 0050 0100];r muti_objective_fuzzy_analysis(x);% 各指标在决策中占的权重(专家系统,自…...

单链表--C语言版(从0开始,超详细解析,小白一看就会)
目录 一、前言 🍎 为什么要学习链表 💦顺序表有缺陷 💦 优化方案:链表 二、链表详解 🍐链表的概念 🍉链表的结构组成:节点 🍓链表节点的连接(逻辑结构与物理结构的区…...
)
cv2-特征点匹配(bf、FLANN)
cv2-特征点匹配(bf、KNN、FLANN) 文章目录cv2-特征点匹配(bf、KNN、FLANN)1. 暴力匹配法(bf)1.1 bf.match()1.2 bf.knnMatch()3. FLANN匹配法4. 总结1. 暴力匹配法(bf) (…...
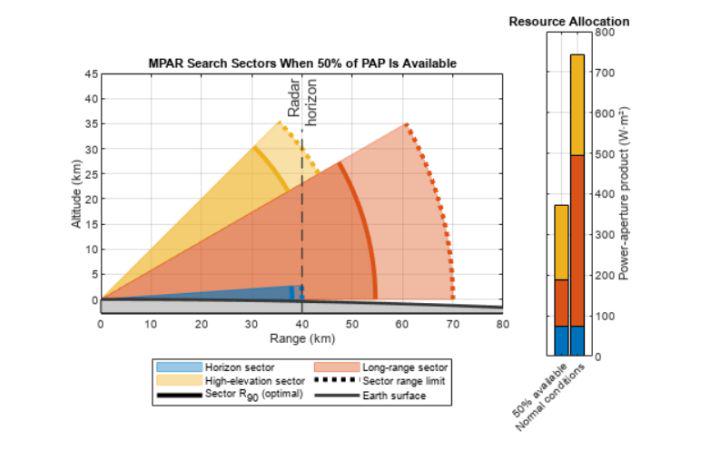
基于matlab多功能相控阵雷达资源管理的服务质量优化
一、前言此示例说明如何为基于服务质量 (QoS) 优化的多功能相控阵雷达 (MPAR) 监控设置资源管理方案。它首先定义必须同时调查的多个搜索扇区的参数。然后,它介绍了累积检测范围作为搜索质量的度量,并展示了…...
立创eda专业版学习笔记(6)(pcb板移动节点)
先要看一个设置方面的东西: 进入设置-pcb-通用 我鼠标放到竖着的线上面,第一次点左键是这样选中的: 再点一次左键是这样选中的: 这个时候,把鼠标放到转角的地方,点右键,就会出现对于节点的选项…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
