图论14-最短路径-Dijkstra算法+Bellman-Ford算法+Floyed算法
文章目录
- 0 代码仓库
- 1 Dijkstra算法
- 2 Dijkstra算法的实现
- 2.1 设置距离数组
- 2.2 找到当前路径的最小值 curdis,及对应的该顶点cur
- 2.3 更新权重
- 2.4 其他接口
- 2.4.1 判断某个顶点的连通性
- 2.4.2 求源点s到某个顶点的最短路径
- 3使用优先队列优化-Dijkstra算法
- 3.1 设计内部类node
- 3.2 入队
- 3.3 记录路径
- 3.4 整体
- 4 Bellman-Ford算法
- 4.1 松弛操作
- 4.2 负权环
- 4.3 算法思想
- 4.4 进行V-1次松弛操作
- 4.5 判断负权环
- 4.6 整体
- 5 Floyed算法
- 5.1 设置记录两点最短距离的数组,并初始化两点之间的距离
- 5.2 更新两点之间的距离
0 代码仓库
https://github.com/Chufeng-Jiang/Graph-Theory/tree/main/src/Chapter11_Min_Path
1 Dijkstra算法
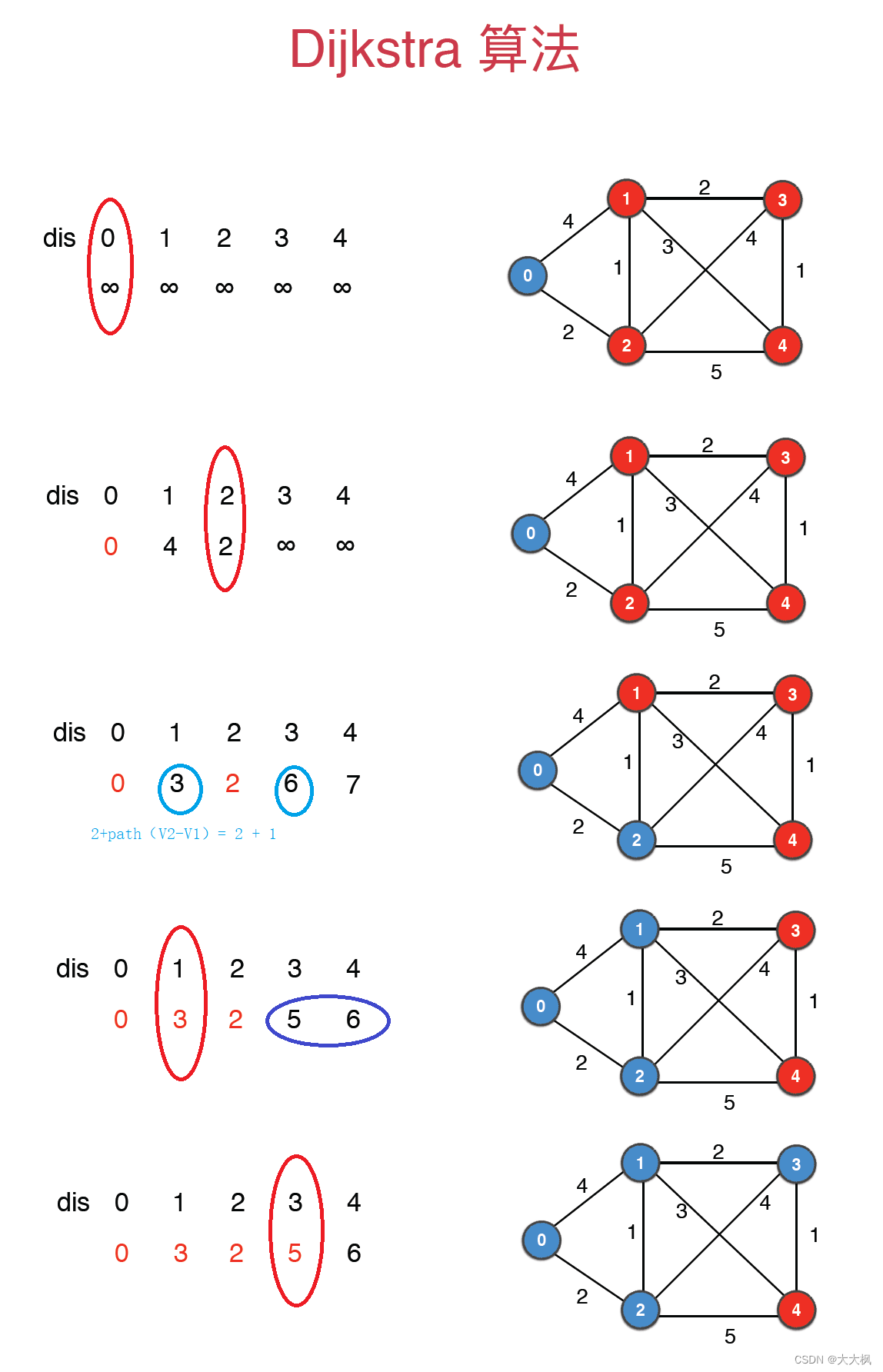
2 Dijkstra算法的实现
2.1 设置距离数组
//用于存储从源点到当前节点的距离,并初始化
dis = new int[G.V()];
Arrays.fill(dis, Integer.MAX_VALUE);
dis[s] = 0;
2.2 找到当前路径的最小值 curdis,及对应的该顶点cur
int cur = -1, curdis = Integer.MAX_VALUE;for(int v = 0; v < G.V(); v ++)if(!visited[v] && dis[v] < curdis){curdis = dis[v];cur = v;}
2.3 更新权重
visited[cur] = true;
for(int w: G.adj(cur))if(!visited[w]){if(dis[cur] + G.getWeight(cur, w) < dis[w])dis[w] = dis[cur] + G.getWeight(cur, w);}
2.4 其他接口
2.4.1 判断某个顶点的连通性
public boolean isConnectedTo(int v){G.validateVertex(v);return visited[v];
}
2.4.2 求源点s到某个顶点的最短路径
public int distTo(int v){G.validateVertex(v);return dis[v];
}
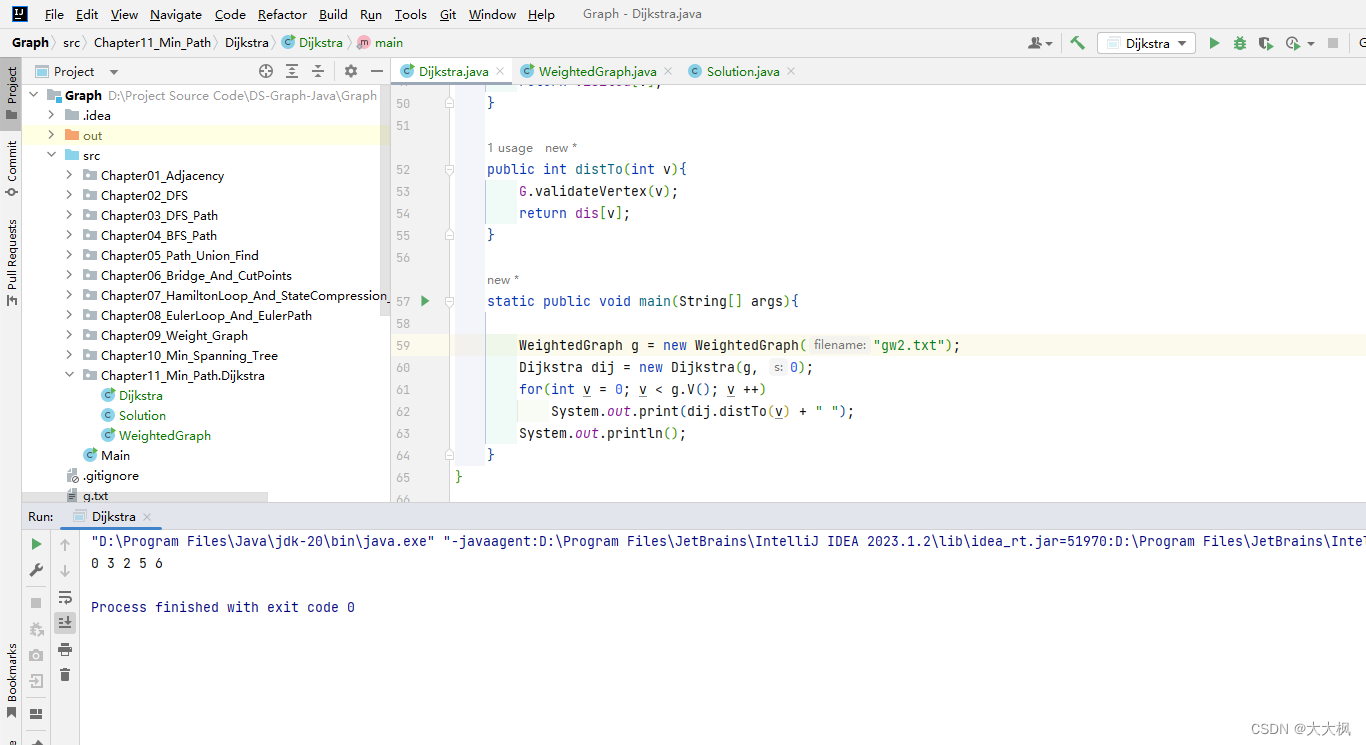
3使用优先队列优化-Dijkstra算法
3.1 设计内部类node
存放节点编号和距离
private class Node implements Comparable<Node>{public int v, dis;public Node(int v, int dis){this.v = v;this.dis = dis;}@Overridepublic int compareTo(Node another){return dis - another.dis;}}
3.2 入队
PriorityQueue<Node> pq = new PriorityQueue<Node>();pq.add(new Node(s, 0));
这里的缺点就是,更新node时候,会重复添加节点相同的node,但是路径值不一样。不影响最后结果。
while(!pq.isEmpty()){int cur = pq.remove().v;if(visited[cur]) continue;visited[cur] = true;for(int w: G.adj(cur))if(!visited[w]){if(dis[cur] + G.getWeight(cur, w) < dis[w]){dis[w] = dis[cur] + G.getWeight(cur, w);pq.add(new Node(w, dis[w]));pre[w] = cur;}}
}
3.3 记录路径
private int[] pre;
- 更新pre数组
for(int w: G.adj(cur))if(!visited[w]){if(dis[cur] + G.getWeight(cur, w) < dis[w]){dis[w] = dis[cur] + G.getWeight(cur, w);pq.add(new Node(w, dis[w]));pre[w] = cur;}}
- 输出路径
public Iterable<Integer> path(int t){ArrayList<Integer> res = new ArrayList<>();if(!isConnectedTo(t)) return res;int cur = t;while(cur != s){res.add(cur);cur = pre[cur];}res.add(s);Collections.reverse(res);return res;}
3.4 整体
package Chapter11_Min_Path.Dijkstra_pq;import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.PriorityQueue;public class Dijkstra {private WeightedGraph G;private int s;private int[] dis;private boolean[] visited;private int[] pre;private class Node implements Comparable<Node>{public int v, dis;public Node(int v, int dis){this.v = v;this.dis = dis;}@Overridepublic int compareTo(Node another){return dis - another.dis;}}public Dijkstra(WeightedGraph G, int s){this.G = G;G.validateVertex(s);this.s = s;dis = new int[G.V()];Arrays.fill(dis, Integer.MAX_VALUE);pre = new int[G.V()];Arrays.fill(pre, -1);dis[s] = 0;pre[s] = s;visited = new boolean[G.V()];PriorityQueue<Node> pq = new PriorityQueue<Node>();pq.add(new Node(s, 0));while(!pq.isEmpty()){int cur = pq.remove().v;if(visited[cur]) continue;visited[cur] = true;for(int w: G.adj(cur))if(!visited[w]){if(dis[cur] + G.getWeight(cur, w) < dis[w]){dis[w] = dis[cur] + G.getWeight(cur, w);pq.add(new Node(w, dis[w]));pre[w] = cur;}}}}public boolean isConnectedTo(int v){G.validateVertex(v);return visited[v];}public int distTo(int v){G.validateVertex(v);return dis[v];}public Iterable<Integer> path(int t){ArrayList<Integer> res = new ArrayList<>();if(!isConnectedTo(t)) return res;int cur = t;while(cur != s){res.add(cur);cur = pre[cur];}res.add(s);Collections.reverse(res);return res;}static public void main(String[] args){WeightedGraph g = new WeightedGraph("g.txt");Dijkstra dij = new Dijkstra(g, 0);for(int v = 0; v < g.V(); v ++)System.out.print(dij.distTo(v) + " ");System.out.println();System.out.println(dij.path(3));}
}4 Bellman-Ford算法
4.1 松弛操作
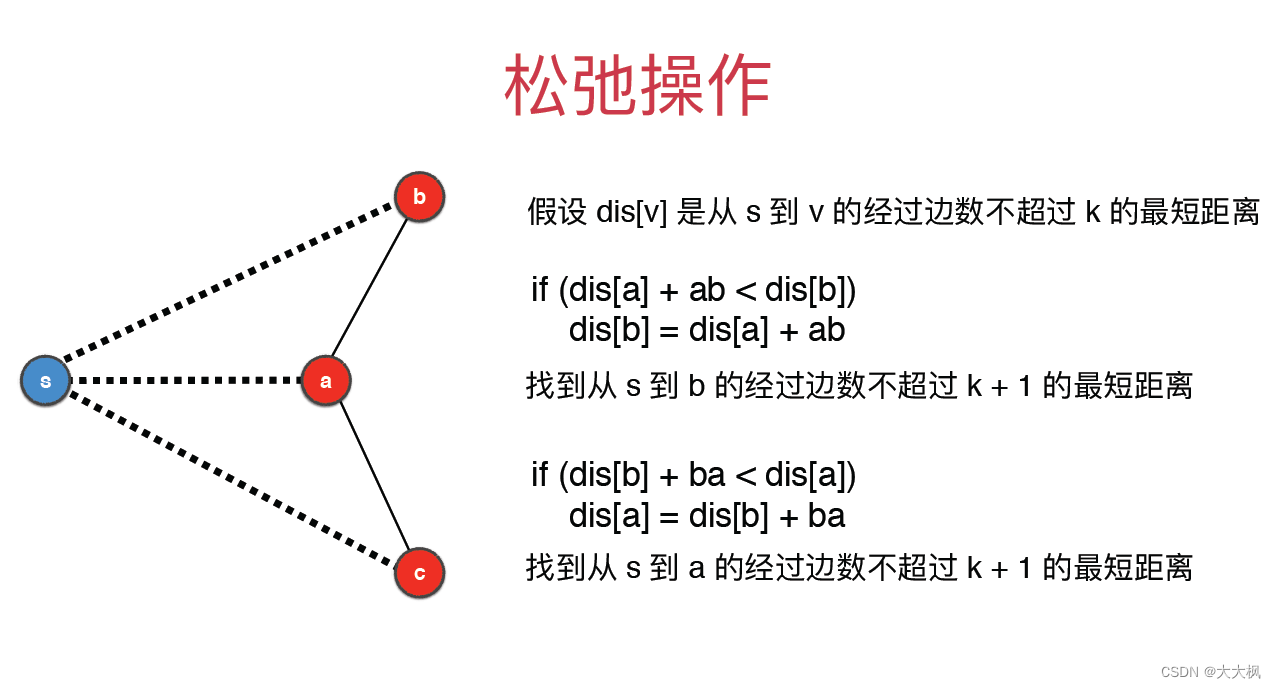
4.2 负权环
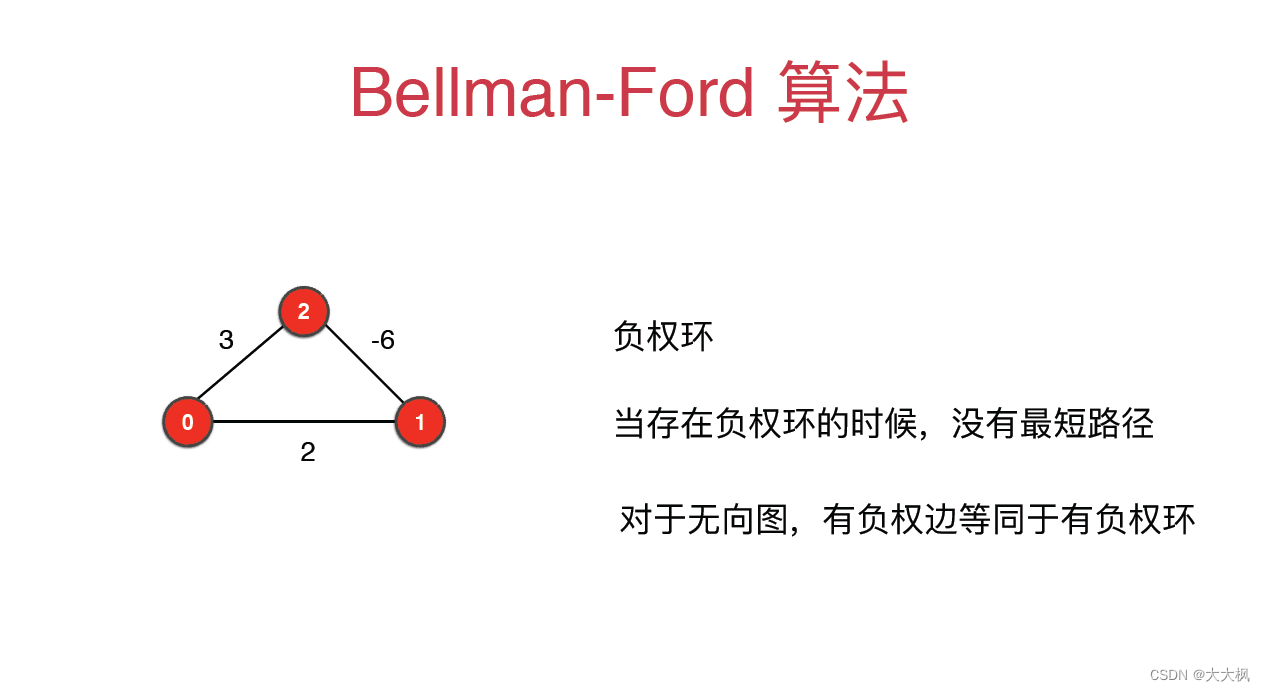
4.3 算法思想

4.4 进行V-1次松弛操作
// 进行V-1次松弛操作
for(int pass = 1; pass < G.V(); pass ++){for(int v = 0; v < G.V(); v ++)for(int w: G.adj(v))if(dis[v] != Integer.MAX_VALUE && // 避免对无穷值的点进行松弛操作dis[v] + G.getWeight(v, w) < dis[w]){dis[w] = dis[v] + G.getWeight(v, w);pre[w] = v;}
}
4.5 判断负权环
// 多进行一次操作,如果还有更新,那么存在负权换
for(int v = 0; v < G.V(); v ++)for(int w : G.adj(v))if(dis[v] != Integer.MAX_VALUE &&dis[v] + G.getWeight(v, w) < dis[w])hasNegCycle = true;
4.6 整体
package Chapter11_Min_Path.BellmanFord;import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;public class BellmanFord {private WeightedGraph G;private int s;private int[] dis;private int[] pre;private boolean hasNegCycle = false;public BellmanFord(WeightedGraph G, int s){this.G = G;G.validateVertex(s);this.s = s;dis = new int[G.V()];Arrays.fill(dis, Integer.MAX_VALUE);dis[s] = 0;pre = new int[G.V()];Arrays.fill(pre, -1);// 进行V-1次松弛操作for(int pass = 1; pass < G.V(); pass ++){for(int v = 0; v < G.V(); v ++)for(int w: G.adj(v))if(dis[v] != Integer.MAX_VALUE && // 避免对无穷值的点进行松弛操作dis[v] + G.getWeight(v, w) < dis[w]){dis[w] = dis[v] + G.getWeight(v, w);pre[w] = v;}}// 多进行一次操作,如果还有更新,那么存在负权换for(int v = 0; v < G.V(); v ++)for(int w : G.adj(v))if(dis[v] != Integer.MAX_VALUE &&dis[v] + G.getWeight(v, w) < dis[w])hasNegCycle = true;}public boolean hasNegativeCycle(){return hasNegCycle;}public boolean isConnectedTo(int v){G.validateVertex(v);return dis[v] != Integer.MAX_VALUE;}public int distTo(int v){G.validateVertex(v);if(hasNegCycle) throw new RuntimeException("exist negative cycle.");return dis[v];}public Iterable<Integer> path(int t){ArrayList<Integer> res = new ArrayList<Integer>();if(!isConnectedTo(t)) return res;int cur = t;while(cur != s){res.add(cur);cur = pre[cur];}res.add(s);Collections.reverse(res);return res;}static public void main(String[] args){WeightedGraph g = new WeightedGraph("gw2.txt");BellmanFord bf = new BellmanFord(g, 0);if(!bf.hasNegativeCycle()){for(int v = 0; v < g.V(); v ++)System.out.print(bf.distTo(v) + " ");System.out.println();System.out.println(bf.path(3));}elseSystem.out.println("exist negative cycle.");WeightedGraph g2 = new WeightedGraph("g2.txt");BellmanFord bf2 = new BellmanFord(g2, 0);if(!bf2.hasNegativeCycle()){for(int v = 0; v < g2.V(); v ++)System.out.print(bf2.distTo(v) + " ");System.out.println();}elseSystem.out.println("exist negative cycle.");}
}5 Floyed算法

5.1 设置记录两点最短距离的数组,并初始化两点之间的距离
private int[][] dis;
- 初始化两点之间的距离
for(int v = 0; v < G.V(); v ++){dis[v][v] = 0;for(int w: G.adj(v))dis[v][w] = G.getWeight(v, w);
}
5.2 更新两点之间的距离
第一重循环:测试两点之间经过点t是否存在更短的路径。
for(int t = 0; t < G.V(); t ++)for(int v = 0; v < G.V(); v ++)for(int w = 0; w < G.V(); w ++)if(dis[v][t] != Integer.MAX_VALUE && dis[t][w] != Integer.MAX_VALUE&& dis[v][t] + dis[t][w] < dis[v][w])dis[v][w] = dis[v][t] + dis[t][w];

相关文章:

图论14-最短路径-Dijkstra算法+Bellman-Ford算法+Floyed算法
文章目录 0 代码仓库1 Dijkstra算法2 Dijkstra算法的实现2.1 设置距离数组2.2 找到当前路径的最小值 curdis,及对应的该顶点cur2.3 更新权重2.4 其他接口2.4.1 判断某个顶点的连通性2.4.2 求源点s到某个顶点的最短路径 3使用优先队列优化-Dijkstra算法3.1 设计内部类…...
OpenCV 实现透视变换
一:OpenCV透视变换的概念 仿射变换(affine transform)与透视变换(perspective transform)在图像还原、图像局部变化处理方面有重要意义。通常,在2D平面中,仿射变换的应用较多,而在3D平面中,透视变换又有了自己的一席之…...

ChinaSoft 论坛巡礼|开源软件供应链论坛
2023年CCF中国软件大会(CCF ChinaSoft 2023)由CCF主办,CCF系统软件专委会、形式化方法专委会、软件工程专委会以及复旦大学联合承办,将于2023年12月1-3日在上海国际会议中心举行。 本次大会主题是“智能化软件创新推动数字经济与社…...

VUE 组合式API
响应式 data 选项式API_响应式 <template><h3>选项式API</h3><p>{{ message }}</p> </template> <script> export default {data(){return{message:"选项式API 绑定数据"}} } </script>组合式API_响应式 <…...
尝试使用php给pdf添加水印
在开发中增加pdf水印的功能是很常见的,经过实验发现这中间还是会有很多问题的。第一种模式,采用生成图片的方式把需要添加的内容保存成图片,再将图片加到pdf中间,这种方法略麻烦一些,不过可以解决中文乱码的问题&#…...
ubuntu上安装edge浏览器
1下载edge浏览器 官网下载 edge浏览器的linux版本可在上面的官网中寻找。 我选择的是Linux(.deb)。 2 安装 可在终端的edge安装包所在的路径下输入下面命令安装。 sudo dpkg -i edge安装包的名称.deb3 安装可能存在的问题 1dpkg:依赖关系问题使得edge-stable的配置工作不…...

动态切换 Spring Boot 打包配置:使用 Maven Profiles 管理 JAR 和 WAR
引言 在多环境开发中,我们经常需要根据部署环境来改变 Spring Boot 应用的打包方式。本文将探讨如何使用 Maven Profiles 结合依赖排除来动态地切换 JAR 和 WAR 打包配置。 1. 修改 pom.xml 以支持 WAR 包 转换 Spring Boot 应用从 JAR 到 WAR 时,首先…...

微信小程序使用阿里巴巴矢量图标
一,介绍 微信小程序使用图标有两种方式,一种是在线获取,一种是下载到本地使用, 第一种在线获取的有个缺点就是图标是灰色的,不能显示彩色图标,而且第一种是每次请求资源的,虽然很快࿰…...
使用JAVA pdf转word
使用spire.pdf 非常简单。 查看 https://mvnrepository.com/artifact/e-iceblue/spire.pdf 注意,这个包在 e-iceblue 下。 下面开始撸代码 先来pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://mav…...

成都瀚网科技有限公司抖音带货的正规
成都瀚网科技有限公司,一家在科技领域有着深厚积累的公司,近年来也开始涉足电子商务领域,特别是在抖音等短视频平台上进行带货活动。在这个充满机遇与挑战的时代,该公司以其独特的商业模式和运营策略,正在赢得消费者的…...

windows服务器热备、负载均衡配置
安装网络负载平衡 需要加入的服务器上全部需要安装网络负载平衡管理器 图形化安装:使用服务器管理器安装 在服务器管理器中,使用“添加角色和功能”向导添加网络负载均衡功能。 完成向导后,将安装 NLB,并且不需要重启计算机。 …...

samba服务器搭建 挂载远程目录 常用配置参数介绍
samba 直接复用linux的用户,但是Linux 用户的密码和 smbpasswd 设置的密码是分开的。 Linux 用户的密码是存储在 Linux 系统的用户数据库中,通常是 /etc/shadow 文件中以加密形式存储的。Samba 用户的密码是存储在专门的 Samba 密码数据库中 smbpasswd…...

Ansible命令使用
ansible ansible的命令 ansible命令模块Pingcommand 模块shell 模块copy 模块file 模块fetch 模块cron 模块yum 模块service 模块user 模块group 模块script 模块setup 模块get_url模块stat模块unarchive模块unarchive模块 ansible的命令 /usr/bin/ansible Ansibe AD-Hoc 临…...
element 周选择器el-date-picker
2023.11.13今天我学习了在使用element 周选择器的时候,我们会发现默认的时间选择为星期日到下一个星期一,如图: 我们需要改成显示星期一到星期天,只需要加一行代码:picker-options <el-date-pickertype"week&…...

No200.精选前端面试题,享受每天的挑战和学习
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…...
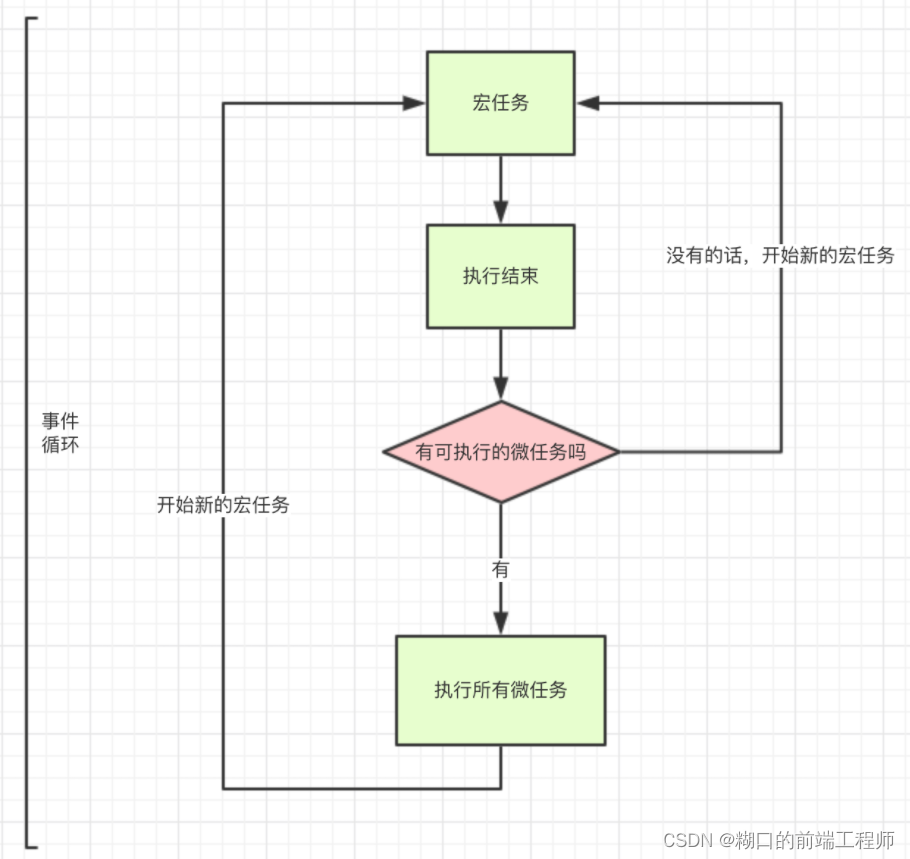
前端面试之事件循环
什么是事件循环 首先, JavaScript是一门单线程的语言,意味着同一时间内只能做一件事,这并不意味着单线程就是阻塞,而是实现单线程非阻塞的方法就是事件循环 在JavaScript中,所欲任务都可以分为: 同步任务…...

sass 封装媒体查询工具
背景 以往写媒体查询可能是这样的: .header {display: flex;width: 100%; }media (width > 320px) and (width < 480px) {.header {height: 50px;} }media (width > 480px) and (width < 768px) {.header {height: 60px;} }media (width > 768px) …...

眼科动态图像处理系统使用说明(2023-8-11 ccc)
眼科动态图像处理系统使用说明 2023-8-11 ccc 动态眼科图像捕捉存贮分析与传输系统,是由计算机软件工程师和医学专家组结合,为满足医院临床工作的需要,在2000年开发的专门用于各类眼科图像自动化分析、处理和传输的软件系统。该系统可以和各…...
国际阿里云:提高CDN缓存命中率教程!!!
CDN缓存命中率低会导致源站压力大,静态资源访问效率低。您可以根据导致CDN缓存命中率低的具体原因,选择对应的优化策略来提高CDN的缓存命中率。 背景信息 CDN通过将静态资源缓存在CDN节点上实现资源访问加速。当客户端访问某资源时,如果CDN节…...

关于“谈谈你对 ES 的理解”
普通人 它是一个基于 Apache Lucene 开源的一个分布式搜索引擎框架。 一般用它来做 ● 日志记录和分析 ● 公共数据采集 ● 全文检索 ● 数据可视化分析等等 高手 Elasticsearch ,简称 ES 。它是建立在全文搜索引擎库 Apache Lucene 基础之上的一个开源的搜索…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
