基于连续Hopfield神经网络优化——旅行商问题优化计算
大家好,我是带我去滑雪!
利用神经网络解决组合优化问题是神经网络应用的一个重要方面。所谓组合优化问题,就是在给定约束条件下,使目标函数极小(或极大)的变量组合问题。将Hopfield网络应用于求解组合优化问题,把目标函数转化为网络的能量函数,把问题的变量对应到网络的状态,这样,当网络的能量函数收敛于极小值时,问题的最优解也随之求出。由于神经网络是并行计算的,其计算量不随维数的增加而发生指数性“爆炸”,因而对于组合优化问题的高速计算特别有效。典型的组合优化问题有旅行商问题、0-1背包问题、装箱问题、图着色问题、聚类问题等问题。这些问题的描述都非常简单,但优化求解很困难,其主要原因是求解这些问题的算法运行时,需要极长的运行时间和极大的存储空间。
本期使用连续Hopfield神经网络实现旅行商问题优化计算。
一、问题与模型设计
(1)问题描述
旅行商问题,(Traveling Saleman Problem,TSP)是VRP的特例,由于Gaery[1]已证明TSP问题是NP难题,因此,VRP也属于NP难题。旅行商问题(TSP)又译为旅行推销员问题、货郎担问题,简称为TSP问题,是最基本的路线问题,该问题是在寻求单一旅行者由起点出发,通过所有给定的需求点之后,最后再回到原点的最小路径成本。
现对于一个城市数量为10的TSP问题,要求设计一个可以对其组合优化的连续型Hopfield神经网络模型,利用改模型可以快速地找到最优(或者近似最优)的一条路线。
(2)模型建立思路
由于连续型Hopfield神经网络具有优化计算的特性,因此将TSP问题的目标函数(即最短路径)与网络的能量函数相对应,将经过的城市顺序与网络的神经元状态相对应。这样,由连续型Hopfield神经网络的稳定性定理知,当网络的能量函数趋于最小值时,网络的神经元状态也趋于平衡点,此时对应的城市顺序即为最佳的路线。
(3)设计步骤
模型映射:为了将TSP问题映射为一个神经网络的动态过程,Hopfield神经网络采取换位矩阵的表示方式,用NxN的矩阵表示商人访问N个城市。对于N个城市TSP问题,使用NxN个神经元来实现,而每行每列只能有一个1,其余都是0,矩阵中1的和为N,该矩阵成为换位矩阵。
构造网络能量函数和动态方程:设计的Hopfield神经网络的能量函数与目标函数(即最短路径)相对应的。同时,考虑到有效解的实际意义,即换位矩阵的每行每列都只能有一个1。因此,网络的能量函数包含目标项和约束项两部分。
初始化网络:Hopfield神经网络迭代过程对网络的能量函数及动态方程的系数十分敏感,在总结前人经验及多次实验的基础上,网络输入初始化选取如下:A=200,D=100,采样时间设置为0.0001,迭代次数为10000。
优化计算:当网络的结果及参数设计完成后,迭代优化计算的过程就变得非常简单,具体步骤:
步骤1:导入N个城市的位置坐标并计算城市之间的距离;
步骤2:网络初始化;
步骤3:计算能量函数;
步骤4:判断迭代次数是否结束,若迭代次数大于10000,则终止。
二、代码实现
(1)清空环境变量、声明全局变量
clear all
clc
global A D(2)城市位置导入并计算城市间距离
load city_location
distance = dist(citys,citys');(3)初始化网络
N = size(citys,1);
A = 200;
D = 100;
U0 = 0.1;
step = 0.0001;
delta = 2 * rand(N,N) - 1;
U = U0 * log(N-1) + delta;
V = (1 + tansig(U/U0))/2;
iter_num = 10000;
E = zeros(1,iter_num);(4)寻优迭代
寻优迭代过程包括动态方程计算、输入神经元状态更新、输出神经元状态更新、能量函数计算四个步骤。
for k = 1:iter_num dU = diff_u(V,distance);U = U + dU*step;V = (1 + tansig(U/U0))/2;e = energy(V,distance);E(k) = e;
end(5)动态方程计算
function du=diff_u(V,d)
global A D
n=size(V,1);
sum_x=repmat(sum(V,2)-1,1,n);
sum_i=repmat(sum(V,1)-1,n,1);
V_temp=V(:,2:n);
V_temp=[V_temp V(:,1)];
sum_d=d*V_temp;
du=-A*sum_x-A*sum_i-D*sum_d;(6)能量函数计算
function E=energy(V,d)
global A D
n=size(V,1);
sum_x=sumsqr(sum(V,2)-1);
sum_i=sumsqr(sum(V,1)-1);
V_temp=V(:,2:n);
V_temp=[V_temp V(:,1)];
sum_d=d*V_temp;
sum_d=sum(sum(V.*sum_d));
E=0.5*(A*sum_x+A*sum_i+D*sum_d);(7)主函数
[rows,cols] = size(V);
V1 = zeros(rows,cols);
[V_max,V_ind] = max(V);
for j = 1:colsV1(V_ind(j),j) = 1;
end
C = sum(V1,1);
R = sum(V1,2);
flag = isequal(C,ones(1,N)) & isequal(R',ones(1,N));%% 结果显示
if flag == 1% 计算初始路径长度sort_rand = randperm(N);citys_rand = citys(sort_rand,:);Length_init = dist(citys_rand(1,:),citys_rand(end,:)');for i = 2:size(citys_rand,1)Length_init = Length_init+dist(citys_rand(i-1,:),citys_rand(i,:)');end% 绘制初始路径figure(1)plot([citys_rand(:,1);citys_rand(1,1)],[citys_rand(:,2);citys_rand(1,2)],'o-')for i = 1:length(citys)text(citys(i,1),citys(i,2),[' ' num2str(i)])endtext(citys_rand(1,1),citys_rand(1,2),[' 起点' ])text(citys_rand(end,1),citys_rand(end,2),[' 终点' ])title(['优化前路径(长度:' num2str(Length_init) ')'])axis([0 1 0 1])grid onxlabel('城市位置横坐标')ylabel('城市位置纵坐标')% 计算最优路径长度[V1_max,V1_ind] = max(V1);citys_end = citys(V1_ind,:);Length_end = dist(citys_end(1,:),citys_end(end,:)');for i = 2:size(citys_end,1)Length_end = Length_end+dist(citys_end(i-1,:),citys_end(i,:)');enddisp('最优路径矩阵');V1% 绘制最优路径figure(2)plot([citys_end(:,1);citys_end(1,1)],...[citys_end(:,2);citys_end(1,2)],'o-')for i = 1:length(citys)text(citys(i,1),citys(i,2),[' ' num2str(i)])endtext(citys_end(1,1),citys_end(1,2),[' 起点' ])text(citys_end(end,1),citys_end(end,2),[' 终点' ])title(['优化后路径(长度:' num2str(Length_end) ')'])axis([0 1 0 1])grid onxlabel('城市位置横坐标')ylabel('城市位置纵坐标')% 绘制能量函数变化曲线figure(3)plot(1:iter_num,E);ylim([0 2000])title(['能量函数变化曲线(最优能量:' num2str(E(end)) ')']);xlabel('迭代次数');ylabel('能量函数');
elsedisp('寻优路径无效');
end(8)结果输出
优化前的路径:

优化后的路径图:

优化后的路径距离相比于没有优化的路径距离更短。
能量函数变化曲线:
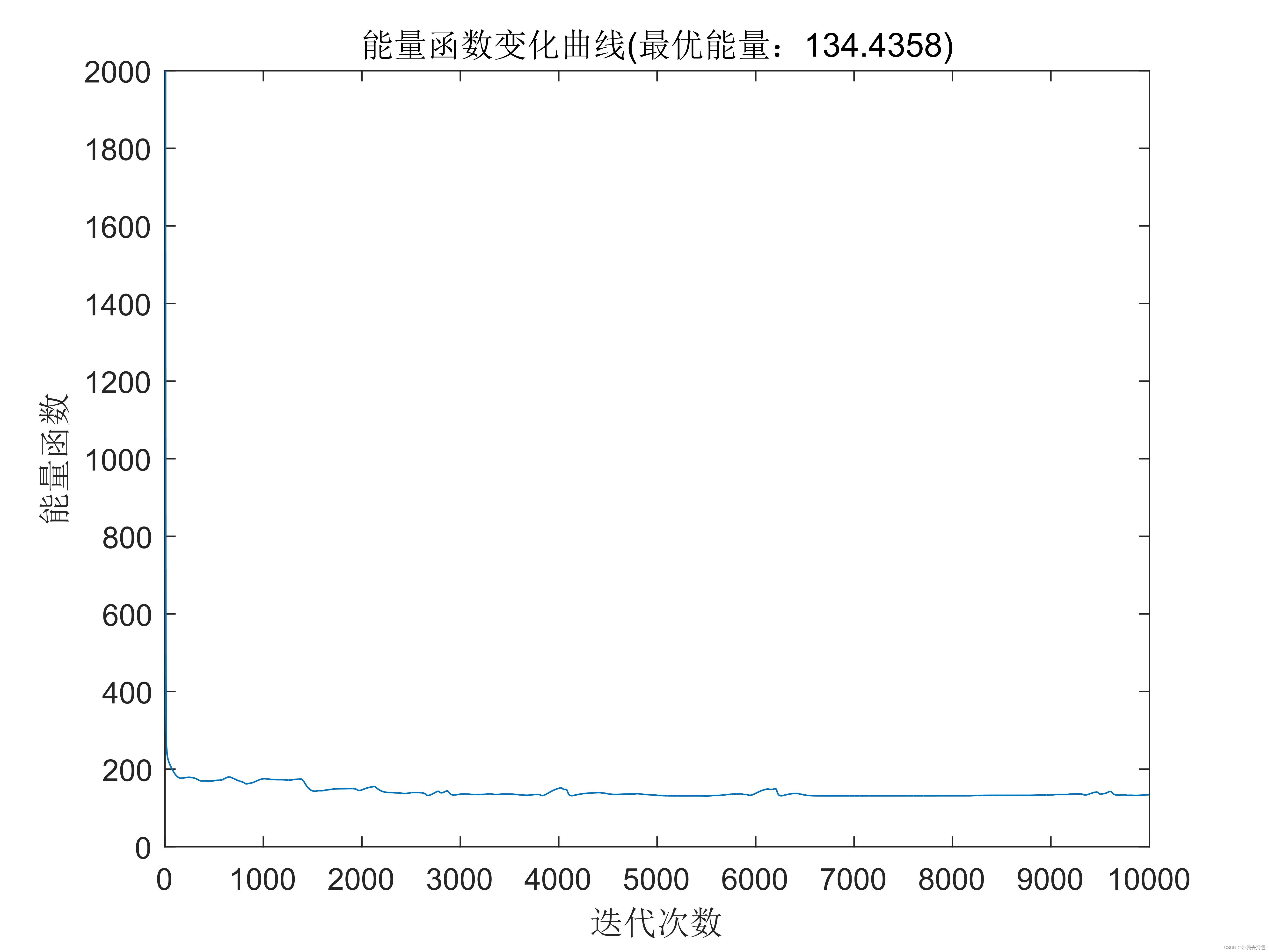
结果表明:利用Hopfield神经网络 ,可以快速准确地解决TSP问题。同理,对于其他利用枚举法会产生“组合爆炸”的组合优化问题,利用连续型Hopfield神经网络也可以进行优化计算。
需要数据集的家人们可以去百度网盘(永久有效)获取:
链接:
提取码:2138
更多优质内容持续发布中,请移步主页查看。
点赞+关注,下次不迷路!
相关文章:

基于连续Hopfield神经网络优化——旅行商问题优化计算
大家好,我是带我去滑雪! 利用神经网络解决组合优化问题是神经网络应用的一个重要方面。所谓组合优化问题,就是在给定约束条件下,使目标函数极小(或极大)的变量组合问题。将Hopfield网络应用于求解组合优化问…...
SpringBoot整合Activiti7——定时器事件(九)
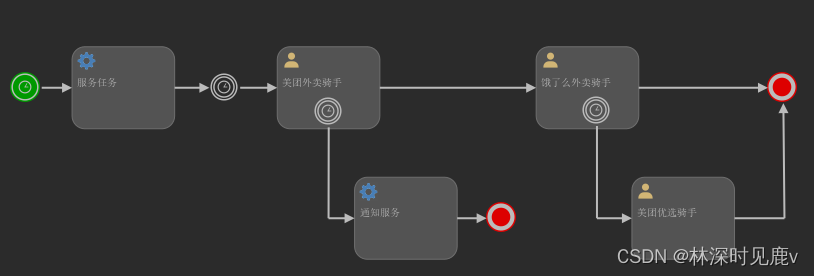
文章目录 定时器事件时间定义时间固定时间段时间周期 1.开始事件2.中间事件3.边界事件代码实现xml文件自定义服务任务监听器自定义用户任务监听器测试流程流程执行步骤 定时器事件 可以用在开始事件、中间事件、边界事件上,边界事件可以是中断和非中断边界事件 需要…...

轻量封装WebGPU渲染系统示例<29>- 深度模糊DepthBlur(源码)
实现方式: step1. 通过mrt机制,输出颜色和深度相关数据的两张rtt纹理。 step2. 基于上述颜色纹理,生成一张模糊之后的新rtt纹理。 setp3. 基于深度(也就是距离摄像机的远近)数据,合成颜色和模糊纹理数据,并最终输出。 当前示例…...

LeetCode226. Invert Binary Tree
文章目录 一、题目二、题解2.1 前序遍历版本2.2 中序遍历版本2.3 后序遍历版本 一、题目 Given the root of a binary tree, invert the tree, and return its root. Example 1: Input: root [4,2,7,1,3,6,9] Output: [4,7,2,9,6,3,1] Example 2: Input: root [2,1,3] Ou…...

Java设计模式-创建型模式-建造者模式
建造者模式 建造者模式案例与工厂模式的区别:Builder 注解 建造者模式 建造者模式是将一个复杂对象的构件与表示分离,使得同样的构件过程可以创建不同的表示。 建造者模式将内部构件的创建和组装分割开,一般使用链式编程,代码整洁…...
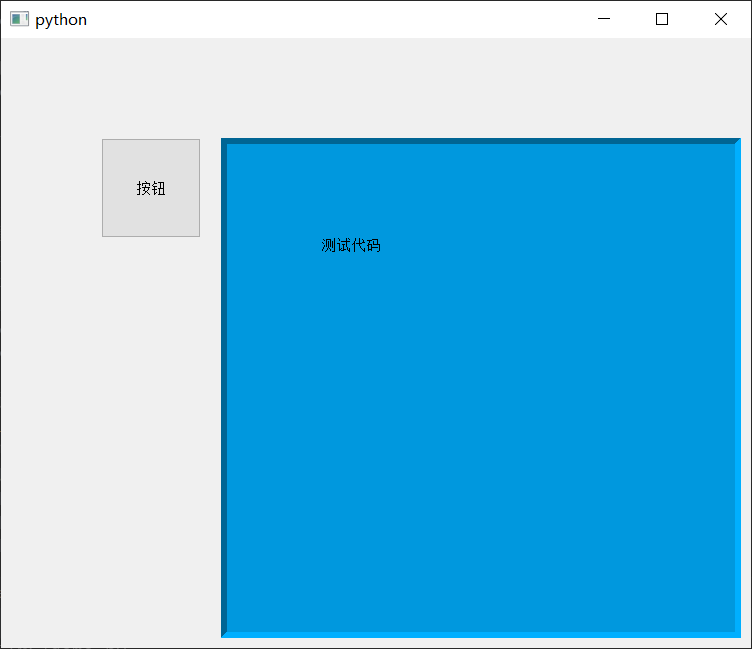
PyQt中QFrame窗口中的组件不显示的原因
文章目录 问题代码(例)原因和解决方法 问题代码(例) from PyQt5.QtWidgets import * from PyQt5.QtGui import QFont, QIcon, QCursor, QPixmap import sysclass FrameToplevel(QFrame):def __init__(self, parentNone):super().…...
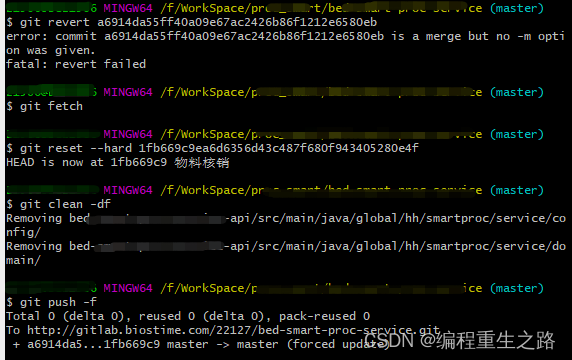
git 命令行回退版本
git 命令行回退版本 git 命令行回退版本命令: 1.切换到需要回退的分支 git checkout branch-v2.0.02.更新远程分支 git fetch3.找到需要回退版本的版本号git revert a6914da55ff40a09e67ac2426b86f1212e6580eb4.清除工作区缓存git clean -df5.强制提交git push -f...

IntelliJ IDEA 安装 GitHub Copilot插件 (最新)
注意: GitHub Copilot 插件对IDEA最低版本要求是2021.2,建议直接用2023.3,一次到位反正后续要升级的。 各个版本的依赖关系,请参照: ##在线安装: 打开 IntelliJ IDEA扩展商店,输入 "Git…...

viewpage选择器
GitHub - hackware1993/MagicIndicator: A powerful, customizable and extensible ViewPager indicator framework. As the best alternative of ViewPagerIndicator, TabLayout and PagerSlidingTabStrip —— 强大、可定制、易扩展的 ViewPager 指示器框架。是ViewPagerIndi…...

vue中如何将json数组指定的key赋值给el-form-item并均匀的分成2列
在Vue中,你可以使用v-for指令来遍历JSON数组,并将指定的key赋值给el-form-item。下面是一个示例: <template><el-form><el-row><el-col :span"6" v-for"item in jsonArray" :key"item.key&qu…...
笔记本分屏怎么操作?3个方法提高工作效率!
“有朋友知道笔记本怎么才能实现分屏吗?我在工作时,经常需要来回切换屏幕,效率真的太低了,有什么方法可以实现两个屏幕同时使用吗?” 在现代生活中,多任务处理已成为常态,而笔记本分屏技术为用户…...

Android 使用poi生成Excel ,word并保存在指定路径内
一添加依赖(一定要用新版依赖防止一些bug) minSdk 26 //注意最小支持SDK26 dependencies {implementation org.apache.poi:poi:5.2.4implementation org.apache.poi:poi-ooxml:5.2.4implementation javax.xml.stream:stax-api:1.0-2 }二,创…...
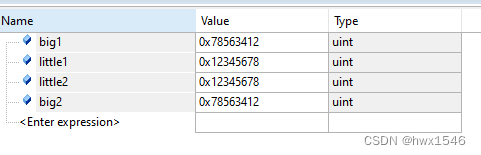
嵌入式杂记 -- MCU的大小端模式
MCU的大小端模式 大端模式小端模式大小端模式测试联合体概念MCU大小端模式测试大端模式测试小端模式测试 大小端模式转换 在进行MCU开发的时候,我们需要注意MCU的数据存储模式,在嵌入式中有两种不同的存储模式,分别是 大端模式和小端模式。 …...

对这套BI零售数据分析方案心动,是零售人天性
零售数据分析做了这么多年,难道真的没累积点经验,摸索出一条又快又能满足绝大多数需求的数据分析捷径?别人不知道,奥威BI还真就有这么一套标准化的BI零售数据分析方案,不管是服装零售、医药连锁、商超都能利用这套方案…...

vuekeyclock 集成
前端集成keycloak鉴权的主要写法, 在main.js里面写 import VueKeycloakJs from dsb-norge/vue-keycloak-js import { KeycloakInstance } from "keycloak-js";// 回调地址 const pageIndex process.env.NODE_ENV production ? http://xxxx/#/ : http:…...

ARM Linux 基础学习 / 配置交叉编译工具链 / 编译 Linux 应用和驱动 / 编译内核
编辑整理 by Staok。 本文部分内容摘自 “100ask imx6ull” 开发板的配套资料(如 百问网的《嵌入式Linux应用开发完全手册》,在 百问网 imx6ull pro 开发板 页面 中的《2.1 100ASK_IMX6ULL_PRO:开发板资料》或《2.2 全系列Linux教程…...
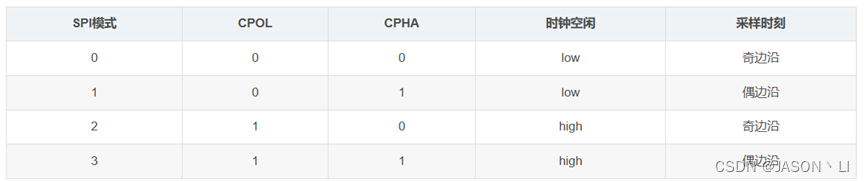
通讯协议学习之路(实践部分):SPI开发实践
通讯协议之路主要分为两部分,第一部分从理论上面讲解各类协议的通讯原理以及通讯格式,第二部分从具体运用上讲解各类通讯协议的具体应用方法。 后续文章会同时发表在个人博客(jason1016.club)、CSDN;视频会发布在bilibili(UID:399951374) 本文…...
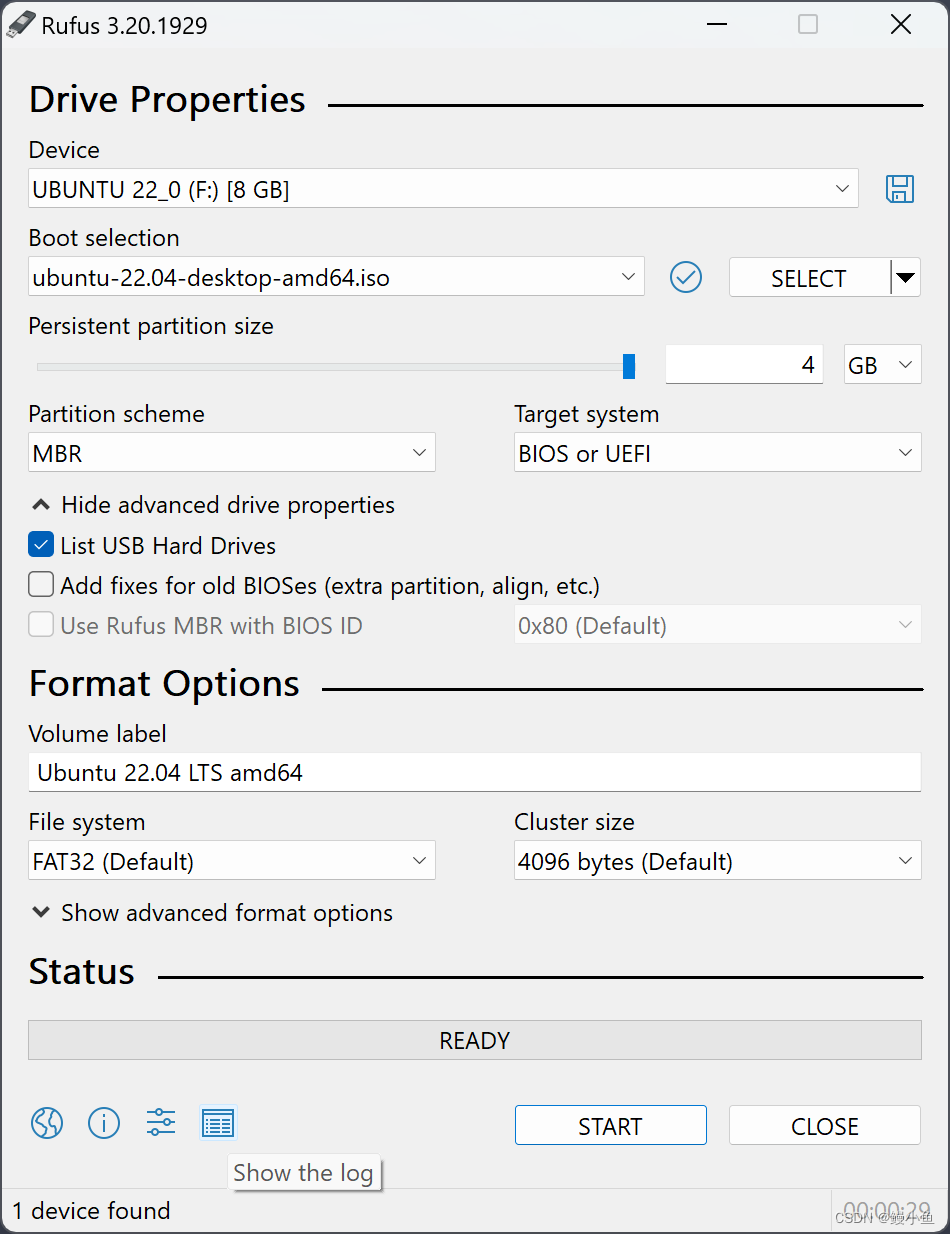
【系统安装】ubuntu20.04启动盘制作,正经教程,小白安装教程,百分百成功安装
1.所需材料: 64GBU盘(其实8g和16g也可以) 2.制作U盘启动盘 使用windows制作ubuntu 20.04启动盘 1)下载制作工具:Rufus:Rufus - 轻松创建 USB 启动盘 2)插入用来做启动盘的U盘 3࿰…...

2023云计算发展趋势
目录 一、云计算是什么? 二、云计算发展趋势 三、总结 一、云计算是什么? 云计算是一种基于互联网的计算方式,通过网络连接的方式提供计算能力、存储服务、应用程序和数据资源。它通常通过虚拟化技术实现多个计算机资源的池化,…...

C# .NET Core API Controller以及辅助专案
准备工作 Windows 10Visual Studio 2019(2017就有可以集中发布到publish目录的功能了吧)C#将方法封装(据说可以提高效率,就像是我们用的dll那种感觉新增专案作为我们API的辅助专案(作用类似dll,此处,你也可以在你自己的API专案里建文件夹,但…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
