[PyTorch][chapter 62][强化学习-基本概念]
前言:
目录:
- 强化学习概念
- 马尔科夫决策
- Bellman 方程
- 格子世界例子
一 强化学习
强化学习 必须在尝试之后,才能发现哪些行为会导致奖励的最大化。
当前的行为可能不仅仅会影响即时奖赏,还有影响下一步奖赏和所有奖赏
强化学习五要素如下:
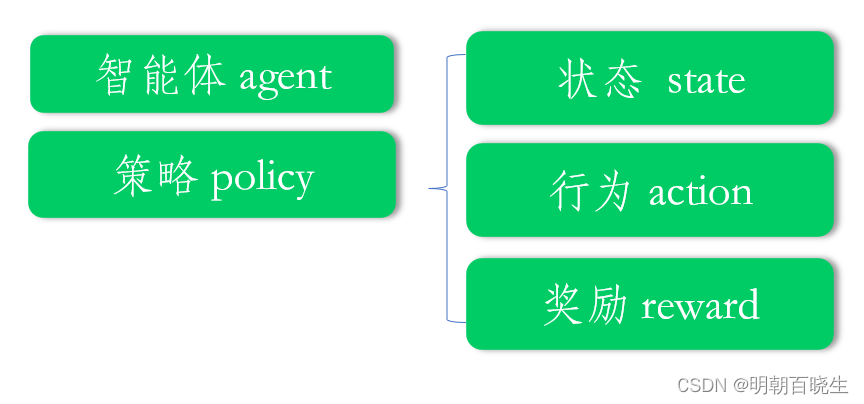
1.2 强化学习流程

1: 产生轨迹(trajectory)
2: 策略评估(policy-evaluate)
3: 策略提升(policy-improve)
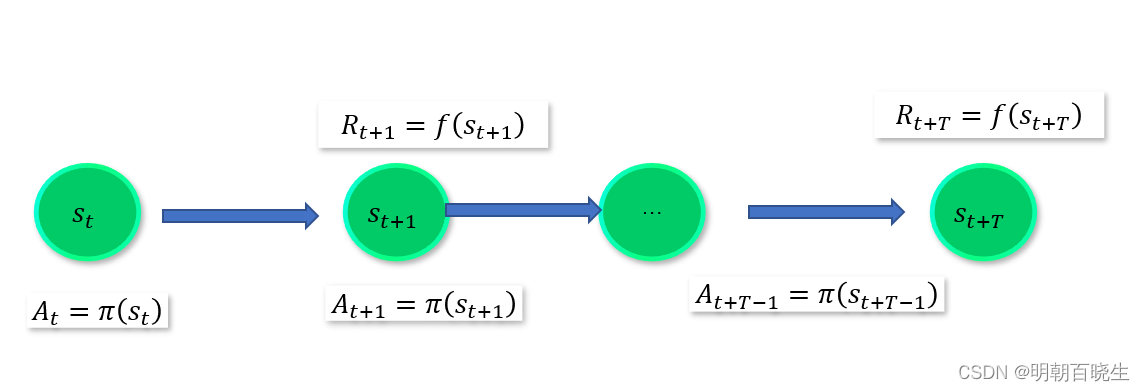
这里重点讲一下 产生轨迹:
当前处于某个state 下面,
按照策略选择 action =
根据新的state 给出 reward:
最后产生了轨迹链
二 马尔科夫决策
2.1 马尔科夫决策要求:
1: 能够检测到理想的状态
2: 可以多次尝试
3: 系统的下个状态只与当前信息有关,与更早的状态无关。
决策过程中还可和当前采取的动作有关.
2.2 马尔科夫决策五要素
S: 状态集合 states
A: 动作集合 actions
P: 状态转移概率
R: 奖励函数(reward function) ,agent 采取某个动作后的及时奖励
r: 折扣系数意味当下的reward 比未来反馈更重要
2.3 主要流程
1: Agent 处于状态
2: 按照策略 选择动作
3:执行该动作后,有一定的概率转移到新的状态

2.4 价值函数
当前时刻处于状态s,未来获得期望的累积奖赏
分为两种: state 价值函数 state-action 价值函数
最优价值函数:
不同策略下, 累积奖赏最大的
2.5 策略 policy
当前状态s 下,按照策略,要采用的动作
三 Bellman 方程
4.1 状态值函数为:
: T 步累积奖赏
:
折扣累积奖赏,
4.2 Bellman 方程
证明:
r折扣奖赏bellman 方程
四 格子世界例子
在某个格子,执行上下左右步骤,其中步骤最短的
为最优路径
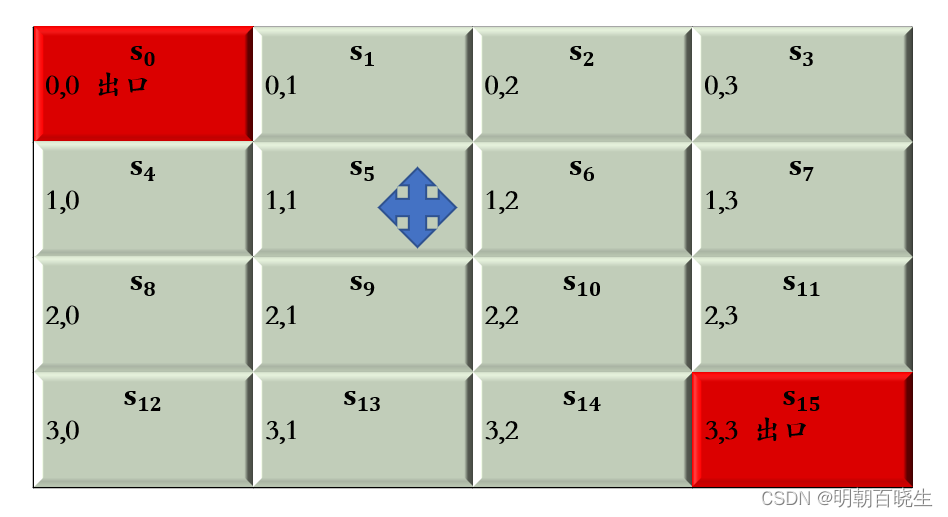
5.1:gridword.py
import numpy as np#手动输入格子的大小
WORLD_SIZE = 4
START_POS = [0,0]
END_POS = [WORLD_SIZE-1, WORLD_SIZE-1]
prob = 1.0
#折扣因子
DISCOUNT = 0.9
# 动作集={上,下,左,右}
ACTIONS = [np.array([0, -1]), #leftnp.array([-1, 0]), # upnp.array([0, 1]), # rightnp.array([1, 0])] # downclass GridwordEnv():def action_name(self, action):if action ==0:name = "左"elif action ==1:name = "上"elif action ==2:name = "右"else:name = "上"return namedef __init__(self):self.nA = 4 #action:上下左右self.nS = 16 #state: 16个状态self.S = []for i in range(WORLD_SIZE):for j in range(WORLD_SIZE):state =[i,j]self.S.append(state)def step(self, s, a):action = ACTIONS[a]state = self.S[s]done = Falsereward = 0.0next_state = (np.array(state) + action).tolist()if (next_state == START_POS) or (state == START_POS):next_state = START_POSdone = Trueelif (next_state == END_POS) or (state == START_POS):next_state = END_POSdone = Trueelse:x, y = next_state# 判断是否出界if x < 0 or x >= WORLD_SIZE or y < 0 or y >= WORLD_SIZE:reward = -1.0next_state = stateelse:reward = -1.0return prob, next_state, reward,done
5.2 main.py
# -*- coding: utf-8 -*-
"""
Created on Mon Nov 13 09:39:37 2023@author: chengxf2
"""import numpy as npdef init_state(WORLD_SIZE):S =[]for i in range(WORLD_SIZE):for j in range(WORLD_SIZE):state =[i,j]S.append(state) print(S)# -*- coding: utf-8 -*-
"""
Created on Fri Nov 10 16:48:16 2023@author: chengxf2
"""import numpy as np
import sys
from gym.envs.toy_text import discrete #环境
from enum import Enum
from gridworld import GridwordEnvclass Agent():def __init__(self,env):self.discount_factor = 1.0 #折扣率self.theta = 1e-3 #最大偏差self.S = []self.env = env#当前处于的位置,V 累积奖赏def one_step_lookahead(self,s, v):R = np.zeros((env.nA)) #不同action的累积奖赏for action in range(env.nA):prob, next_state,reward, done = env.step(s, action) #只有一个next_state_index = self.env.S.index(next_state)#print("\n state",s ,"\t action ",action, "\t new_state ", next_state,"\t next_state_index ", next_state_index,"\t r: ",reward)r= prob*(reward + self.discount_factor*v[next_state_index])R[action] +=r#print("\n state ",s, "\t",R) return Rdef value_iteration(self, env, theta= 1e-3, discount_factor =1.0):v = np.zeros((env.nS)) #不同状态下面的累积奖赏,16个状态iterNum = 0while True:delta = 0.0for s in range(env.nS):R = self.one_step_lookahead(s,v)#在4个方向上面得到的累积奖赏best_action_value = np.max(R)#print("\n state ",s, "\t R ",R, "\t best_action_value ",best_action_value)bias = max(delta, np.abs(best_action_value-v[s]))v[s] =best_action_value#if (s+1)%4 == 0:#print("\n -----s ------------",s)iterNum +=1if bias<theta:breakprint("\n 迭代次数 ",iterNum)return vdef learn(self):policy = np.zeros((env.nS,env.nA))v = self.value_iteration(self.env, self.theta, self.discount_factor)for s in range(env.nS):R = self.one_step_lookahead(s,v)best_action= np.argmax(R)#print(s,best_action_value )policy[s,best_action] = 1.0return policy,vif __name__ == "__main__":env = GridwordEnv()agent =Agent(env)policy ,v = agent.learn()for s in range(env.nS):action = np.argmax(policy[s])act_name = env.action_name(action)print("\n state ",s, "\t action ",act_name, "\t 累积奖赏 ",v[s])参考:
【强化学习玩游戏】1小时竟然就学会了强化学习dqn算法原理及实战(人工智能自动驾驶/深度强化学习/强化学习算法/强化学习入门/多智能体强化学习)_哔哩哔哩_bilibili
2-强化学习基本概念_哔哩哔哩_bilibili
3-马尔科夫决策过程_哔哩哔哩_bilibili
4-Bellman方程_哔哩哔哩_bilibili
5-值迭代求解_哔哩哔哩_bilibili
相关文章:

[PyTorch][chapter 62][强化学习-基本概念]
前言: 目录: 强化学习概念 马尔科夫决策 Bellman 方程 格子世界例子 一 强化学习 强化学习 必须在尝试之后,才能发现哪些行为会导致奖励的最大化。 当前的行为可能不仅仅会影响即时奖赏,还有影响下一步奖赏和所有奖赏 强…...
使用 Stable Diffusion Img2Img 生成、放大、模糊和增强
在线工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 3D数字孪生场景编辑器 Stable Diffusion 2022.1 Img5Img 于 2 年发布,是一款革命性的深度学习模型,正在重新定义和推动照片级真实…...

【Git】第一篇:Git安装(centos)
git查看安装版本 以我自己的centos7.6为例,我们可以输入以下指令查看自己是否安装了git. git --version安装了的话就会显示自己安装的版本。 git 安装 安装很简单,一条命令即可 sudo yum install git -ygit 卸载 sudo yum remove git -y...

在uniapp中通过自定义事件使页面之间传递数据
在uniapp中,可以使用uni.$emit来在页面之间传递数据。uni.emit是一个事件触发器,可以在一个页面中触发一个自定义事件,并在其他页面中监听和处理这个事件。 // A页面 uni.$emit(dataChanged, { message: Hello from A page! });在接收数据的…...
【Windows Docker:安装nginx】
拉镜像 docker pull nginx运行初始镜像 docker run -d -p 80:80 --name nginx nginx拷贝文件 docker cp nginx:/etc/nginx/nginx.conf D:/dockerFile/nginx/nginx.conf docker cp nginx:/etc/nginx/conf.d D:/dockerFile/nginx/conf.d docker cp nginx:/usr/share/nginx/htm…...
ElasticSearch7.x - HTTP 操作 - 查询文档操作
查询索引下的所有文档 http://192.168.254.101:9200/shopping/_search 条件查询 请求路径上添加条件:http://192.168.254.101:9200/shopping/_search?q=category:小米 请求体上添加条件:http://192.168.254.101:9200/shopping/_search 请求体内容 {"query" :{&qu…...
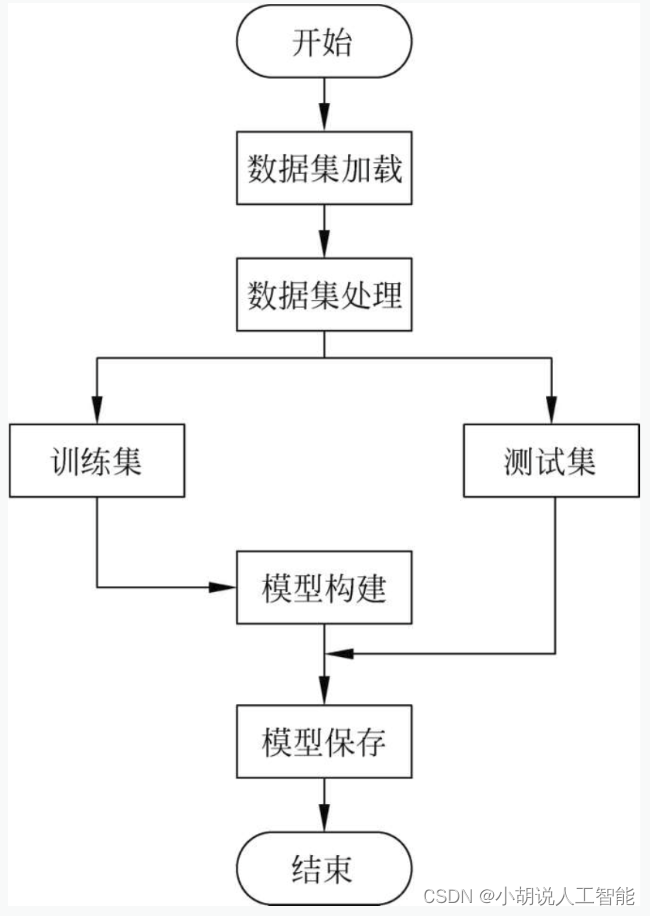
基于opencv+tensorflow+神经网络的智能银行卡卡号识别系统——深度学习算法应用(含python、模型源码)+数据集(一)
目录 前言总体设计系统整体结构图系统流程图 运行环境Python环境TensorFlow 环境OpenCV环境 相关其它博客工程源代码下载其它资料下载 前言 本项目基于从网络获取的多种银行卡数据集,采用OpenCV库的函数进行图像处理,并通过神经网络进行模型训练。最终实…...

如何使用`open-uri`模块
首先,我们需要使用open-uri模块来打开网页,并使用Nokogiri模块来解析网页内容。然后,我们可以使用Nokogiri的css方法来选择我们想要的元素,例如标题,作者,内容等。最后,我们可以使用open-uri模块…...
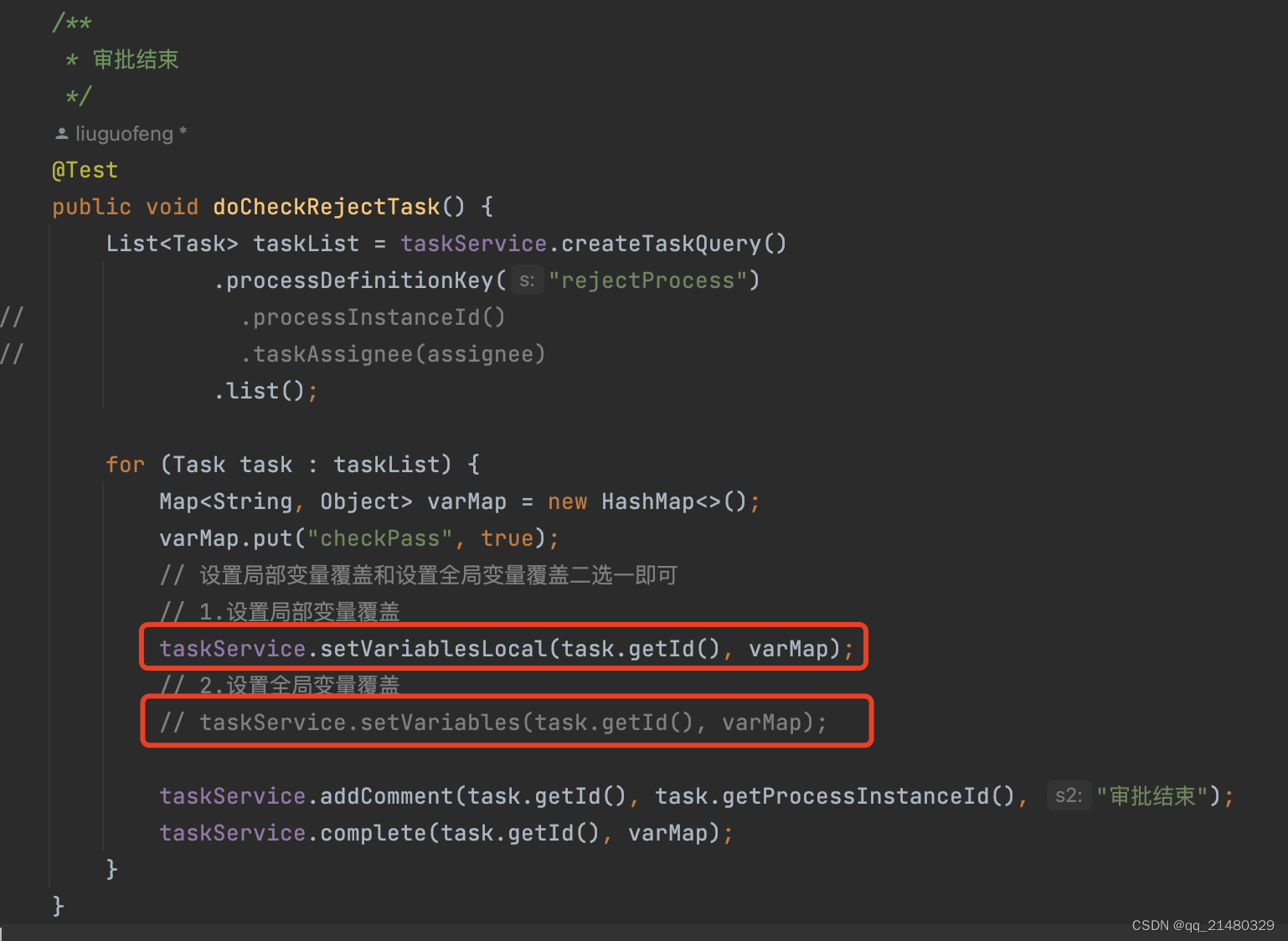
activiti7审批驳回,控制变量无法覆盖,导致无限循环驳回,流程无法结束
项目开发过程中使用工作流,因此考虑使用activiti7做完工作流引擎。项目开发过程中,发现流程驳回时,再次执行流程,控制变量无法覆盖,导致无限循环驳回,流程无法结束。流程图如下图所示: 驳回控制…...

世界互联网大会|云轴科技ZStack受邀分享云原生超融合
11月8日至10日“世界互联网大会乌镇峰会”在浙江嘉兴的乌镇开幕,大会的主题为“建设包容、普惠、有韧性的数字世界——携手构建网络空间命运共同体”,全球各界代表就热点焦点问题展开讨论,反映产业各界对互联网发展的前瞻思考,引领…...
k8s ingress基础
一、ingress 简介 在k8s集群中,service和pod的ip为内网ip,仅集群内部才可以访问。如果外部应用想要直接访问集群内的服务,就需要把外部请求通过负载均衡转发到service上,然后再由kube-proxy组件将其转发给后端pod。一般service可…...
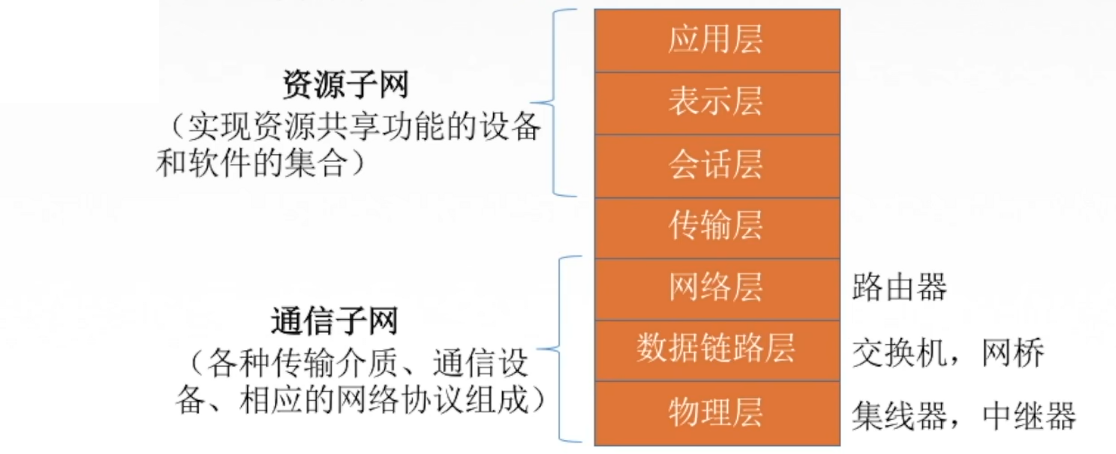
【网络奇缘】我和英特网再续前缘
🌈个人主页: Aileen_0v0🔥系列专栏: 一见倾心,再见倾城 --- 计算机网络~💫个人格言:"没有罗马,那就自己创造罗马~" 目录 计算机网络的概念 计算机网络的功能 ⭐1.数据通信 ⭐2.资源共享 ⭐3.分布式处理 ⭐4.提高可靠性 ⭐…...
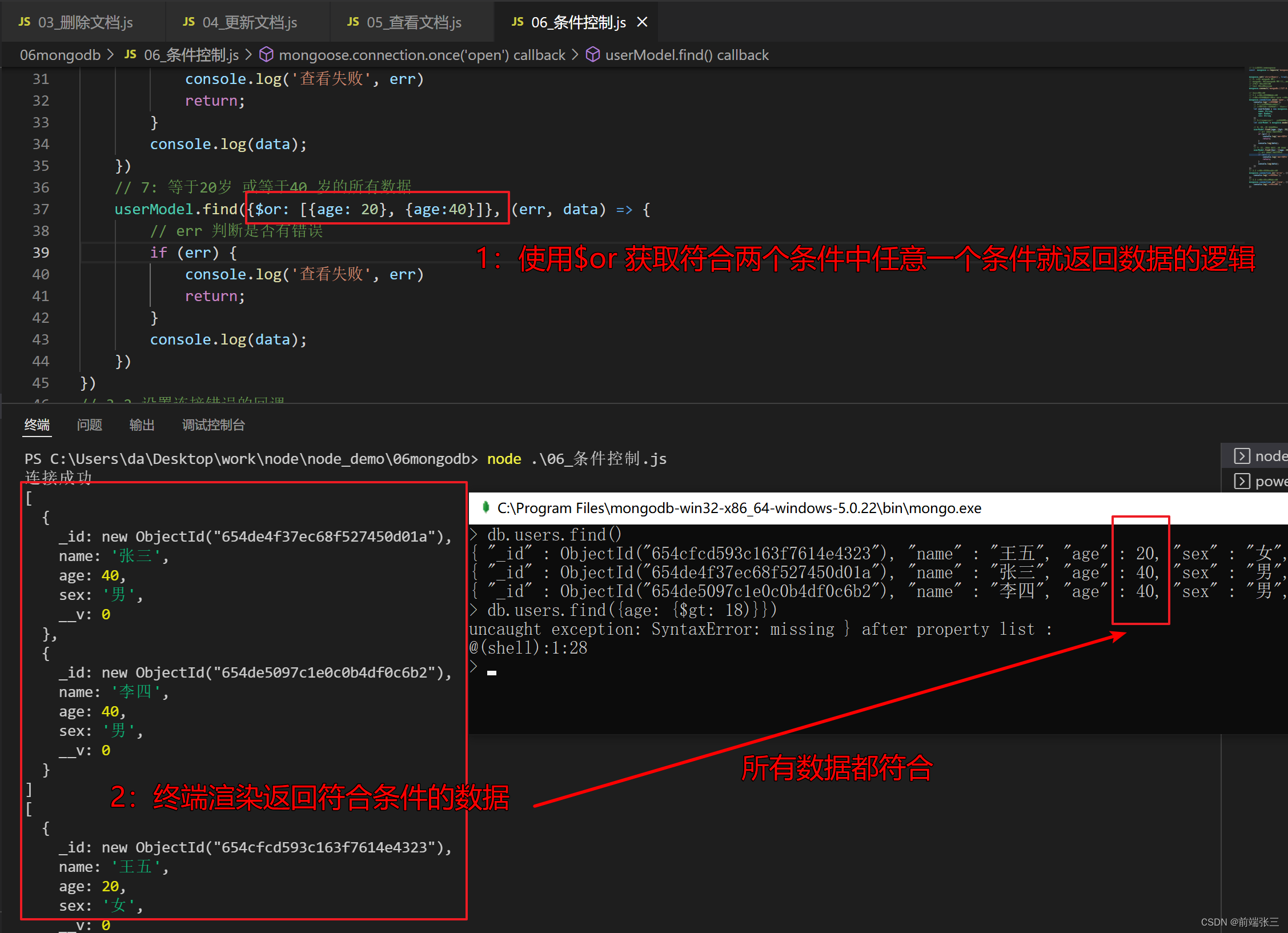
node插件MongoDB(四)—— 库mongoose 的条件控制(三)
文章目录 前言一、运算符二、逻辑运算1. $or 逻辑或2. $and 逻辑与 三、正则匹配 前言 在mongodb 不能使用 > < > < ! 等运算符,需要使用替代符号。 一、运算符 > 使用 $gt< 使用 $lt> 使用 $gte< 使用 $lte! 使用 $ne 例子:获…...
【Amazon】云上探索实验室—了解 AI 编程助手 Amazon Codewhisperer
文章目录 一、前言📢二、关于云上探索实验室🕹️三、领学员需要做什么?✴️四、领学员能获得什么?🔣五、学课通道入口👇1️⃣CSDN平台2️⃣网易云课堂3️⃣Skill Builder 平台 六、活动详情链接 一、前言&a…...

【安卓13】谷歌原生桌面launcher3 禁止桌面图标拖拽和所有应用拖拽
前言 如果我们需要固定住布局,不给用户拖拽,可以通过修改长按点击监听事件来达到禁止拖拽的目的二、代码追踪 1、src/com/android/launcher3/touch/ItemLongClickListener.java 在这个类开头注册了两种类型的监听,一个是在桌面拖拽应用&…...

SA实战 ·《SpringCloud Alibaba实战》第13章-服务网关:项目整合SpringCloud Gateway网关
大家好,我是冰河~~ 一不小心[SpringCloud Alibaba实战》专栏都更新到第13章了,再不上车就跟不上了,小伙伴们快跟上啊! 在《SpringCloud Alibaba实战》专栏前面的文章中,我们实现了用户微服务、商品微服务和订单微服务之间的远程调用,并且实现了服务调用的负载均衡。也基于…...

海外ASO优化之谷歌商店的评论优化
应用商店中的评分和评论,显示我们的应用程序的受欢迎程度以及用户对该应用程序的看法。评分和评论是以前或者是现在的用户分享的经验和公开的反馈。 1、提高应用评分评论。 高评分的应用可以从应用商店内的搜索流量中获得更多的点击量,通过推荐和推荐获…...
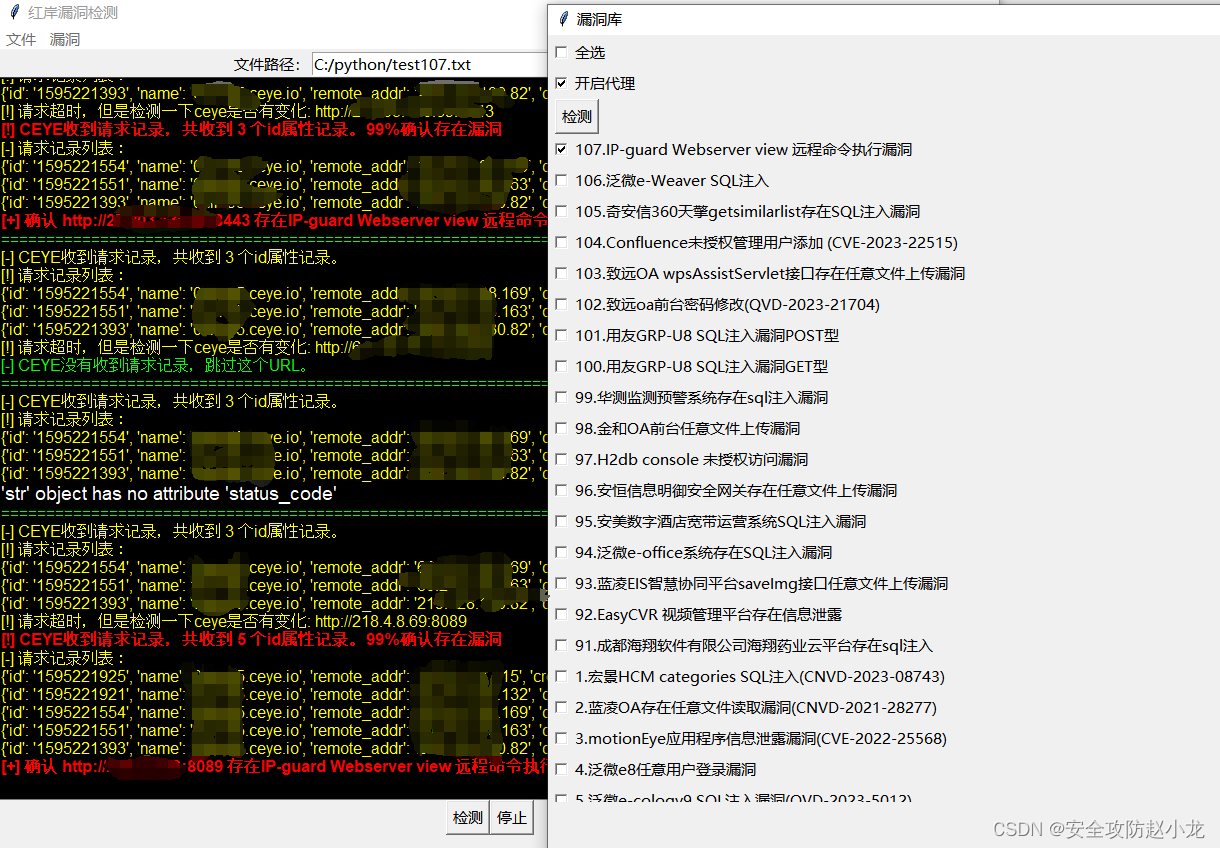
IP-guard Webserver view 远程命令执行漏洞【2023最新漏洞】
IP-guard Webserver view 远程命令执行漏洞【2023最新漏洞】 一、漏洞描述二、漏洞影响三、漏洞危害四、FOFA语句五、漏洞复现1、手动复现yaml pocburp发包 2、自动化复现小龙POC检测工具下载地址 免责声明:请勿利用文章内的相关技术从事非法测试,由于传…...

专访|OpenTiny 社区 Mr 栋:结合兴趣,明确定位,在开源中给自己一些技术性挑战
前言 OpenTiny 开源之夏项目终于迎来了圆满的结局。借此机会,我们采访了 TinyReact 的共建者 Mr 栋同学。 Mr 栋同学是一位热衷于前端技术的开发者,对前端开发充满了激情和热爱。同时他也是一位即将毕业的大四在校生。在 OpenTiny 开源项目中࿰…...
2023年11月PHP测试覆盖率解决方案
【题记:最近进行了ExcelBDD PHP版的开发,查阅了大量资料,发现PHP测试覆盖率解决方案存在不同的历史版本,让我花费了蛮多时间,为了避免后人浪费时间,整理本文,而且网上没有给出Azure DevOps里面P…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...
