每日一题(LeetCode)----数组--长度最小的子数组
每日一题(LeetCode)----数组–长度最小的子数组
1.题目( 209.长度最小的子数组)
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度**。**如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 1091 <= nums.length <= 1051 <= nums[i] <= 105
进阶:
- 如果你已经实现
O(n)时间复杂度的解法, 请尝试设计一个O(n log(n))时间复杂度的解法。
2.解题思路
思路一: 暴力法
暴力法是最直观的方法。初始化子数组的最小长度为无穷大,枚举数组 nums 中的每个下标作为子数组的开始下标,对于每个开始下标 iii,需要找到大于或等于 iii 的最小下标 j,使得从 nums[i] 到 nums[j] 的元素和大于或等于 s,并更新子数组的最小长度(此时子数组的长度是 j−i+1j-i+1j−i+1)。
原作者:力扣官方题解
链接:https://leetcode.cn/problems/backspace-string-compare/
方法二:前缀和 + 二分查找
方法二的时间复杂度是 O(n2),因为在确定每个子数组的开始下标后,找到长度最小的子数组需要 O(n) 的时间。如果使用二分查找,则可以将时间优化到 O(logn)
为了使用二分查找,需要额外创建一个数组 sums 用于存储数组 nums 的前缀和,其中 sums[i]\text{sums}[i]sums[i] 表示从 nums[0] 到 nums[i−1]的元素和。得到前缀和之后,对于每个开始下标 iii,可通过二分查找得到大于或等于 iii 的最小下标 bound,使得 sums[bound]−sums[i−1]≥s,并更新子数组的最小长度(此时子数组的长度是 bound−(i−1))。
因为这道题保证了数组中每个元素都为正,所以前缀和一定是递增的,这一点保证了二分的正确性。如果题目没有说明数组中每个元素都为正,这里就不能使用二分来查找这个位置了。
这里最开始没有看懂,看了力扣上这位网友的评论明白了很多
原作者:力扣官方题解
链接:https://leetcode.cn/problems/backspace-string-compare/

思路三: 滑动窗口
其实滑动窗口就是双指针,我们定义两个指针分别表示滑动窗口的起始位置和结束位置,滑动窗口就是子数组,以此我们就可以求出子数组的总和,看是否符合条件了
初始时滑动窗口的起始位置和结束位置都是数组的首元素,然后我们向右移动滑动窗口的结束位置,相当于是向右遍历一遍数组,每向右移动一位我们都看一下滑动窗口的总和是否大于等于目标值,如果大于我们就计算一下当前子数组长度,然后更新一下答案,之后让滑动窗口的起始位置向后移动一位,直到滑动窗口的总和下于目标值了,我们继续向右遍历,直到遍历结束,得到最终的答案
3.写出代码
思路一的代码:
class Solution {
public:int minSubArrayLen(int s, vector<int>& nums) {int n = nums.size();if (n == 0) {return 0;}int ans = INT_MAX;for (int i = 0; i < n; i++) {int sum = 0;for (int j = i; j < n; j++) {sum += nums[j];if (sum >= s) {ans = min(ans, j - i + 1);break;}}}return ans == INT_MAX ? 0 : ans;}
};原作者:力扣官方题解
链接:https://leetcode.cn/problems/backspace-string-compare/
思路二的代码:
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int length=nums.size();vector<int> sum(length+1,0);int ans=0x7fffffff;//得到前缀和for(int i=1;i<=length;i++){sum[i]=sum[i-1]+nums[i-1];}//遍历得到答案for(int i=1;i<=length;i++){int temp=target+sum[i-1];int bound=lower_bound(sum.begin(),sum.end(),temp)-sum.begin();//注意:lower_bound函数的返回值是第一个大于等于目标值的地址,所以我们这里减去首元素的地址就可以获得第一个大于等于目标值的下标了if(bound<length+1){ans=min(ans,bound-(i-1));}}if(ans==0x7fffffff){return 0;}else{return ans;}}
};
思路三的代码:
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int length=nums.size();int i=0;int sum=0;int result=0x7fffffff;for(int j=0;j<length;j++){sum+=nums[j];while(sum>=target){result=min(result,j-i+1);sum-=nums[i];i++;}}if(result==0x7fffffff){return 0;}else{return result;}}
};
相关文章:

每日一题(LeetCode)----数组--长度最小的子数组
每日一题(LeetCode)----数组–长度最小的子数组 1.题目( 209.长度最小的子数组) 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl1, ..., numsr-1, numsr] &…...
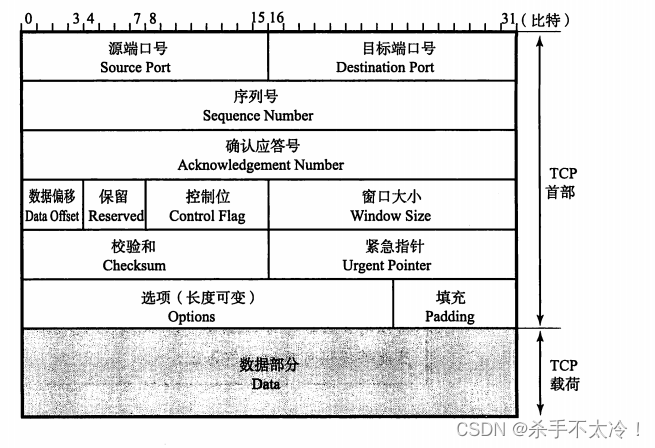
TCP与UDP
文章目录 TCP与UDP传输层的作用端口号UDPTCPUDP首部的格式TCP首部格式 TCP与UDP TCP/IP中有两个具有代表性的传输层协议,它们分别是TCP和UDP。TCP提供可靠的通信传输,而UDP则常被用于让广播和细节控制交给应用的通信传输。总之,根据通信的具…...

js实现对象数组去重
数组去重,一般会在面试的时候才会碰到,要求手写数组去重方法的代码。如果是被提问到,数组去重的方法有哪些?你能答出其中的10种,面试官很有可能对你刮目相看。 在实际项目中碰到的数组去重,一般都是后台去处…...

2023 极术通讯-安谋科技发布“山海”S20F安全解决方案,持续加码智能汽车“芯”赛道
导读:极术社区推出极术通讯,引入行业媒体和技术社区、咨询机构优质内容,定期分享产业技术趋势与市场应用热点。 芯方向 AMBA向多芯片和CHI C2C进发 Arm的Advanced Microcontroller Bus Architecture(AMBA)在与生态系…...

GRPC学习
GRPC元数据 在gRPC中,元数据(metadata)是用于在gRPC请求和响应中传递附加信息的一种机制。元数据是以键值对(key-value pairs)的形式组织的信息,它可以包含请求的上下文信息、安全凭证、消息传输相关的信息…...

c++ latch 使用详解
c latch 使用详解 std::latch c20 头文件 #include <latch>。作用:提供了一种机制,可以让一个或多个线程等待,直到计数器减为零。注意事项: latch 为向下计数器,即只能减少不能增加或者重置。这也使得其只能单…...

linux 下正确使用cp命令复制目录
linux下复制目录时,cp -r 没有 cp -a 好: 使用cp -r 拷贝数据,拷贝的结果是生成新的时间戳等信息 使用cp -a 相当于将原数据原封不动的拷贝过来,不改变里面的任何信息 指定目录时, 源目录/* 【说明:斜…...

CTF----Web真零基础入门
目录 前置知识导图: TCP/IP体系结构(IP和端口): IP是什么:是计算机在互联网上的唯一标识(坐标,代号),用于在互联网中寻找计算机。 内网(局域网…...

css实现元素四周阴影
前言 首先确定的是需要使用box-shadow这一属性 语法如下: box-shadow: h-shadow v-shadow blur spread color inset; h-shadow:表示水平方向上的阴影偏移量,必须指明,可以是正数、负数、0,如果为正数左方有阴影&…...

《QT从基础到进阶·二十五》界面假死处理
假如有这样一种情况,我们在主线程写了一个死循环,当程序运行到主线程的死循环代码后界面便卡死点了没有反应,这里提供几种方法处理界面假死的情况,保证比如主线程在执行死循环没有退出的时候点击界面不会卡死能继续执行其他功能。…...
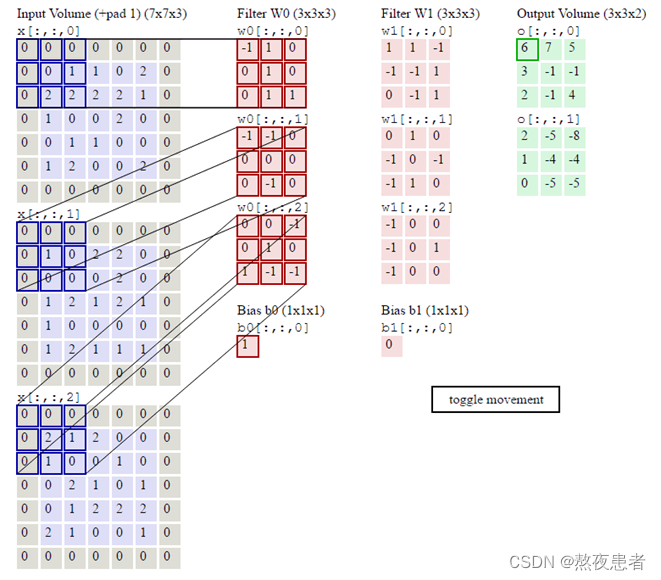
卷积神经网络(1)
目录 卷积 1 自定义二维卷积算子 2 自定义带步长和零填充的二维卷积算子 3 实现图像边缘检测 4 自定义卷积层算子和汇聚层算子 4.1 卷积算子 4.2 汇聚层算子 5 学习torch.nn.Conv2d()、torch.nn.MaxPool2d();torch.nn.avg_pool2d(),简要介绍使用方…...

Mysql中名叫infomaiton_schema的数据库是什么东西?
在 MySQL 中,information_schema 是一个系统数据库,用于存储关于数据库服务器元数据的信息。它并不存储用户数据,而是包含有关数据库、表、列、索引、权限等方面的元数据信息。这些信息可以通过 SQL 查询来获取,用于了解和管理数据…...
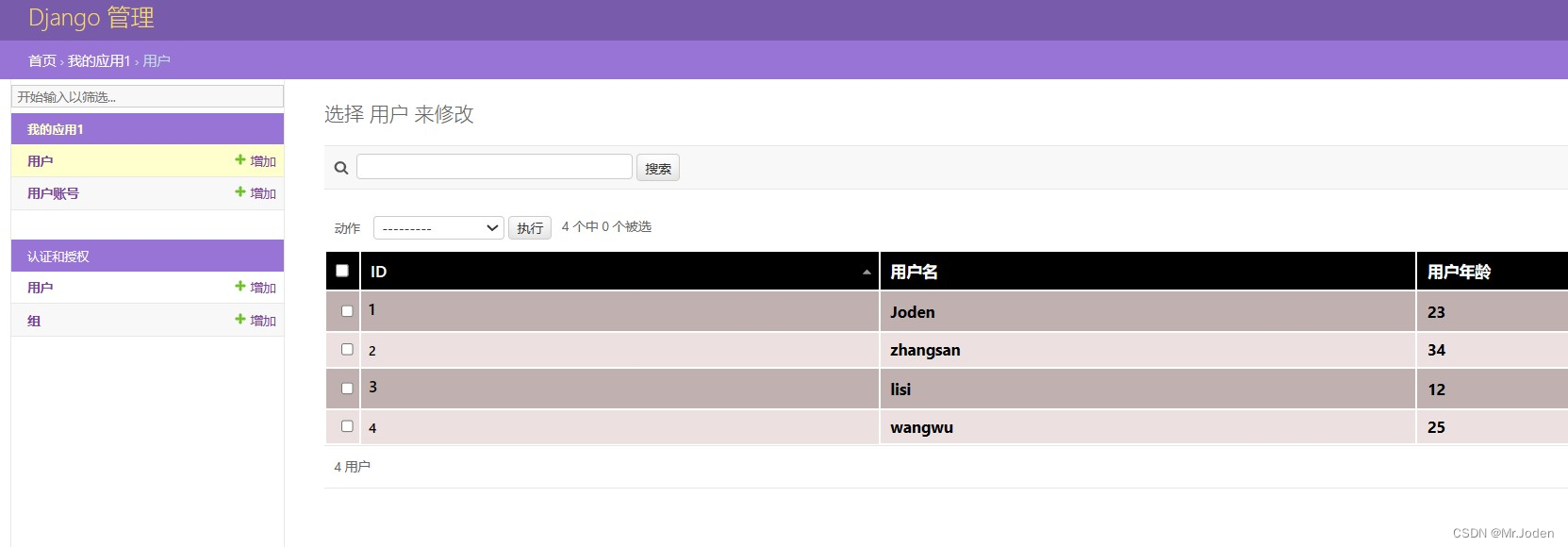
Django(复习篇)
项目创建 1. 虚拟环境 python -m venv my_env cd my_env activate/deactivate pip install django 2. 项目和app创建 cd mypros django-admin startproject Pro1 django-admin startapp app1 3. settings配置INSTALLED_APPS【app1"】TEMPLATES【 DIRS: [os.pat…...

MySQL里对时间的加减操作及常用语法
查询当前时间: select NOW(); //2023-11-14 11:36:03 select CURDATE(); //2023-11-14 SELECT CURTIME(); //11:36:03日期加日期: select date_add(NOW(), interval 1 year); //加1年 select date_add(NOW(), interval 1 month); …...

『MySQL快速上手』-⑨-复合查询
文章目录 1.基本查询回顾2.多表查询案例3.自链接案例4.子查询4.1 单行子查询4.2 多行子查询4.3 多列子查询4.4 在from子句中使用子查询5.合并查询5.1 union5.2 union all6.表的内连和外连6.1 内连接6.2 外连接6.2.1 左外连接6.2.2 右外连接...
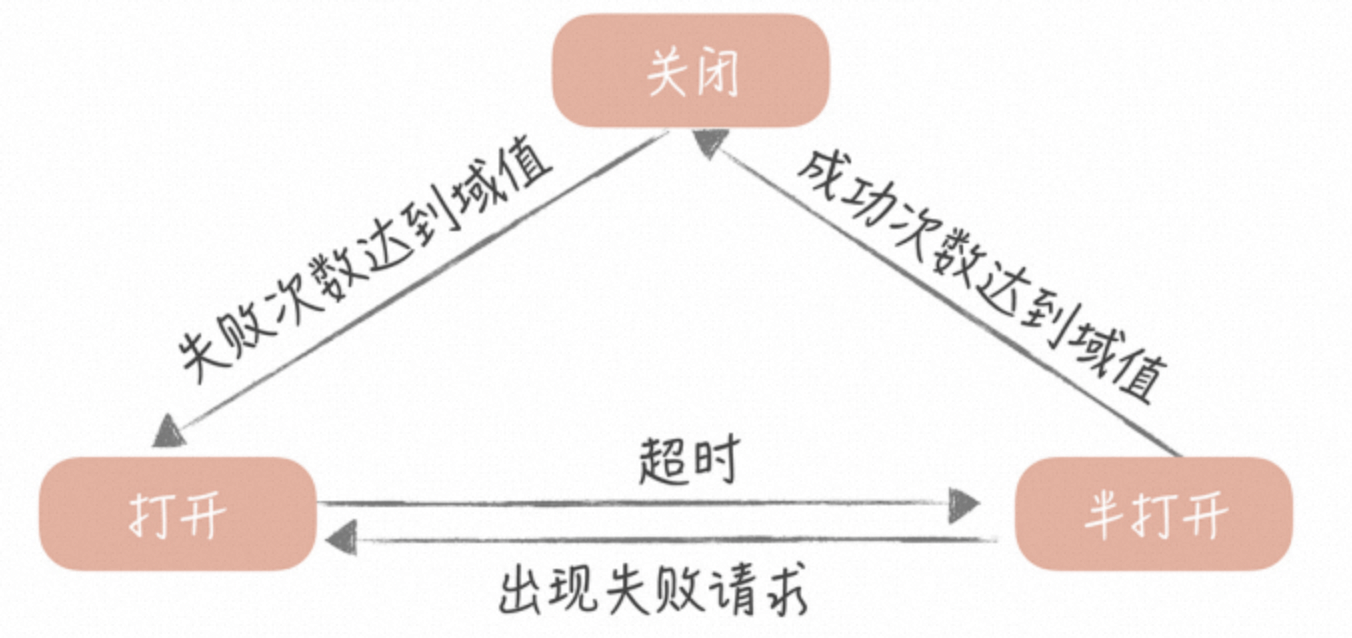
高并发架构设计(三大利器:缓存、限流和降级)
引言 高并发背景 互联网行业迅速发展,用户量剧增,系统面临巨大的并发请求压力。 软件系统有三个追求:高性能、高并发、高可用,俗称三高。三者既有区别也有联系,门门道道很多,全面讨论需要三天三夜&#…...
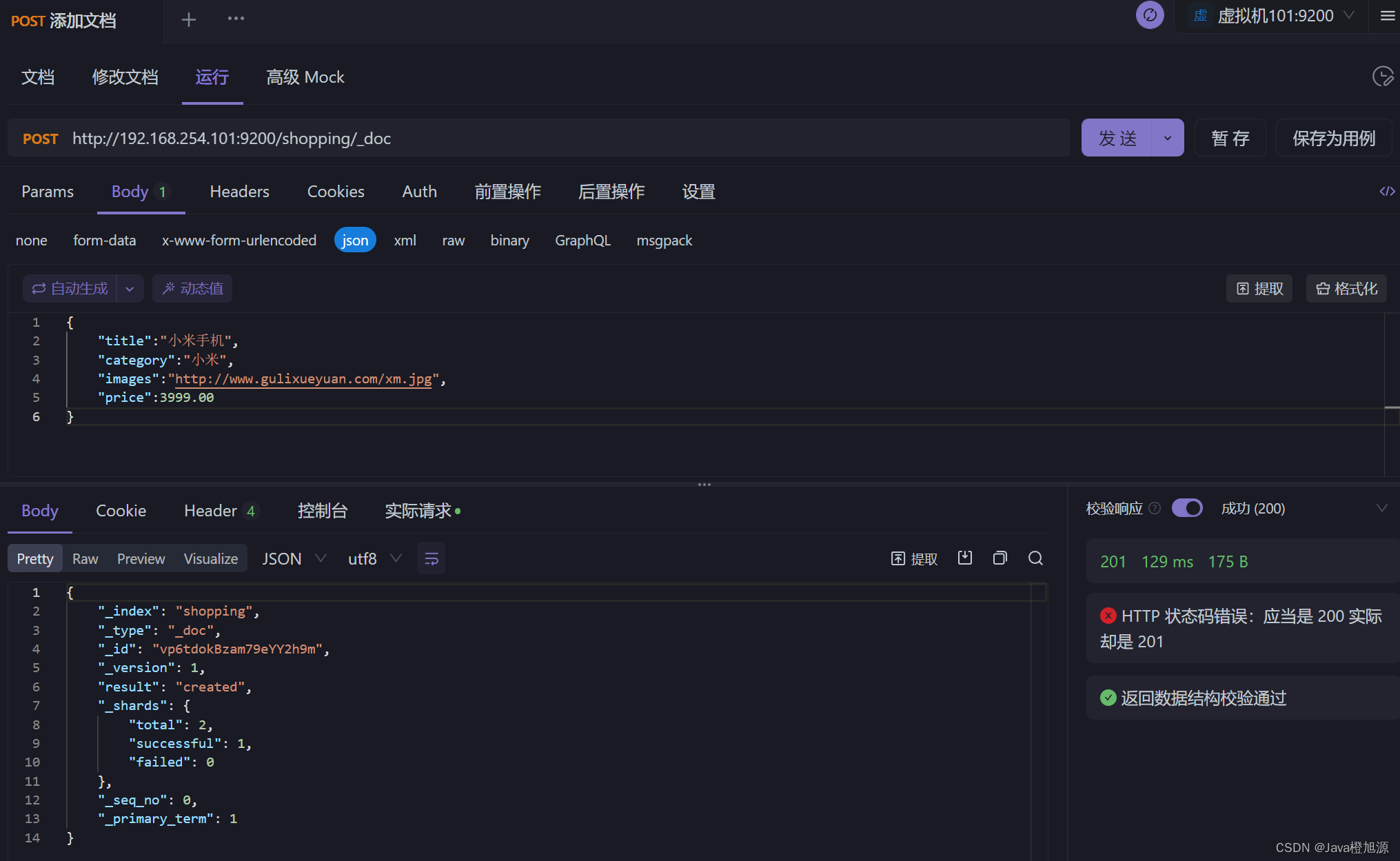
ElasticSearch7.x - HTTP 操作 - 文档操作
创建文档(添加数据) 索引已经创建好了,接下来我们来创建文档,并添加数据。这里的文档可以类比为关系型数 据库中的表数据,添加的数据格式为 JSON 格式 向 ES 服务器发 POST 请求 :http://192.168.254.101:9200/shopping/_doc 请求体内容为: {"title":"小…...
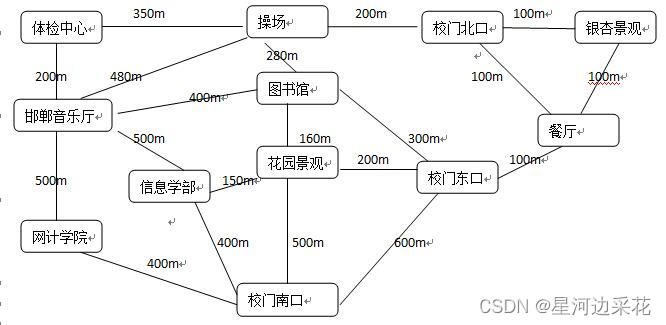
[数据结构大作业]HBU 河北大学校园导航
校园导航实验报告 问题描述: 以我校为例,设计一个校园导航系统,主要为来访的客人提供信息查询。系统有两类登陆账号,一类是游客,使用该系统方便校内路线查询;一类是管理员,可以使用该系统查询…...

立体库堆垛机控制程序手动功能实现
手动操作功能模块 手动前后保护锁 *************提升手动程序段 手动上升,下降保护锁 **********货叉手动程序段...

git commit提交报错
git commit -m 名字’时报一下错误: [FAILED] npm run lint-staged:js [FAILED] [FAILED] npm run lint-staged:js [FAILED] [SUCCESS] Running tasks for staged files..npm ERR! code EPERM npm ERR! syscall open npm ERR! path C:\Program Files\nodejs\node_c…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
