【算法每日一练]-图论(保姆级教程 篇1(模板篇)) #floyed算法 #dijkstra算法 #spfa算法
今天开始讲图论
目录
图的存储
算任意两点的最短路径:
floyed算法:
算一个点到其他所有点的最短距离
dijkstra算法:
spfa算法:
图的存储
其实:邻接矩阵和链式向前星都能存边的信息,vector只能存点的信息,再搭配上v[]便可存点的权值,如果是树的话也建议vector)
邻接矩阵:(可存边信息)
邻接表:vector法(存点信息)(也可以搞一个fa[]存每个点父亲)链式向前星(存边信息)
下面是链式向前星的模板
#include <bits/stdc++.h>
using namespace std;
int tot,n,m;
int head[100];//存放每个点起边的标号
struct edge{int to,w,next;//to是边终点,next是下一条边的标号(不用存起点,因为我们是通过起点来找边号的)
}e[100];//存储边,每条边都有唯一下标
void add(int u,int v,int w){e[++tot].to=v; //这里我们一般从1开始存边,是因为head里面我们默认0时无边 !!!e[tot].w=w;e[tot].next=head[u]; head[u]=tot;//后来的边就插在最前面(这里有个细节:因为最开始head内容是0,所以最后一个边的next一定是0)
}
int main(){int u,v,w;cin>>n>>m; //n个点,m个边for(int i=1;i<=m;i++){cin>>u>>v>>w;add(u,v,w);}for(int x=1;x<=n;x++){//把每个起点都遍历一遍for(int i=head[x];i!=0;i=e[i].next){ //遍历每个点连的边icout<<x<<','<<e[i].to<<'\n';}}
}
算任意两点的最短路径:
floyed算法:
O(n^3) 可以处理负权图,不能判断负环图
思想:从第一个点开始,循环n次,依次加入每个点,看看因为这个点的加入,所有点间距离因此而变小就更新
int main(){ //floyed算法int n;cin>>n;int w[n+1][n+1];memset(w,0x3f,sizeof(w));//若是无向图,对角点初始化为0即可,有联系的点间放权值即可;对角点要初始化for(int k=1;k<=n;k++)//依次放入每个点进行中转,这一层是可以单独拿出来的for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){if(w[i][j]>w[i][k]+w[k][j])//距离变短就更新w[i][j]=w[i][k]+w[k][j]; }
}
算一个点到其他所有点的最短距离
spfa算法:O(nm)=O(KV) 可以处理负权图,判断负环图(负环就是一圈相加起来的权值是个负数)
思想:先将起点加入队列,每次从队列中取出一个点,遍历相邻边找到因该点加入而距离变小的点更新,更新成功的点重新入队,重复至队空
bellman-ford算法:
时间复杂度O(nm) 可以处理负权图,判断负环图
dijkstra算法:
O(n^2)或O(nlogn) 只能处理非负权图
思想:每次贪心地选出一个最小路径的点变成白点(确定点),遍历相邻边找到因该点加入而距离变小的点更新,重复至队空(白点自动会跳过)(如果出现负权,这会直接导致选白点的时候就出错了,因此就不能使用该算法)
题:

dijkstra算法:
(原理:贪心思想,确定白点的过程就是贪心,故不能处理负边权)
1. 初始化dis[s]=0,其余点dis为无穷大.
2. 取出队中dis值最小的蓝点cur,变成白点后遍历周围点v,当dis[cur]+w<dis[v],就更新dis[v] (若cur已为白点,就跳过,这点不同于spfa)
3,被更新的点入队,等待重新更新周围点
4,重复操作,直到队空,也就是所有点都变成了白点
(注意队列一些点的dis值会越来越多,分两种情况:(对蓝点)取出来的一定是可以变成白点的,不用管; (对白点)dis中值一定比队列中的小,我们跳过即可)
我们提供有两种判断办法:
第一种是对出队元素pos的dis和dis[cur]比较,若不相等则说明选出旧白点了,就跳过
第二种方法是对已经成为白点的进行标记,若出队元素早已经是白点了,就跳过
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> pa; //pair中first是距离,second是起点到的它点
const int N=1e5+10,M=2e5+10;
int n,m,s,t,tot;
int pre[N];
int head[N],dis[N],vis[N]; //head[i]存放起点i周围的边号,vis标记此点是否为白点(即已确定的点)
struct edge {int to,w,next; } e[M];//如果N,M没有const修饰,这里要报错的
priority_queue<pa,vector<pa>,greater<pa>> Q; //小根堆,按dis升序排列void add(int u,int v,int w) {e[++tot]=(edge){v,w,head[u]};head[u]=tot;}
void dijkstra(int s) {memset(dis,0x3f,sizeof(dis));dis[s]=0;Q.push(make_pair(0,s)); //make_pair函数的返回值是一个pair,功能是将两个数据合成一个pairwhile (!Q.empty()) {int cur=Q.top().second;Q.pop();//出队就相当于取出最小蓝点if (vis[cur]) continue;//跳过旧白点vis[cur]=1;for (int i=head[cur];i;i=e[i].next) { //i为边号 遍历cur连向周围所有边i的点vint v=e[i].to,w=e[i].w; if (dis[cur]+w<dis[v]) dis[v]=dis[cur]+w,Q.push(make_pair(dis[v],v));//更新后就要入队,等待重新更新周围点}}
}
int main() {cin>>n>>m>>s;int u,v,w;for (int i=1;i<=m;++i) {cin>>u>>v>>w;add(u,v,w);}dijkstra(s);for (int i=1;i<=n;++i) cout<<dis[i]<<' ';return 0;
}
//另一个判断方式+具体路径输出
void print(int u){if(u==0)return;print(pre[u]);cout<<u<<"->";
}
void dijkstra(int s) {memset(dis,0x3f,sizeof(dis));dis[s]=0;Q.push(make_pair(0,s)); while (!Q.empty()) {int pos=Q.top().second,dis_=Q.top().first; Q.pop();if (dis_!=dis[pos]) continue;//跳过旧白点for (int i=head[pos];i;i=e[i].next) { int to=e[i].to,w=e[i].w; if (dis[pos]+w<dis[to]) dis[to]=dis[pos]+w,pre[v]=cur,Q.push(make_pair(dis[to],to));}}
}
main:for (int i=1;i<=n;++i) {cout<<dis[i]<<": ";print(i);cout<<'\n';}
spfa算法步骤:
(原理就是线性dp,由以确定点按拓扑序推下个未确定点,然后未确定点由前面多个以确定点决策,就是按层递推)
1. 初始化dis[s]=0,其余dis为无穷大(vis[s]=1)
2,cur出队,遍历周围点v,当dis[cur]+w<dis[v],就更新dis[v](vis[cur]=0)
3,(松弛,入队)被更新的且不在队伍的点入队,等待重新更新周围点(vis[v]=1)(这一步与dijkstra不同,因为已经入过队的可能还会入队,故可处理负边权)
4,重复操作,直到队空
不过此题卡spfa,但是因为还是要给出来,因为spfa算法可用地方太多了,比如spfa还可以处理最长路问题
#include <bits/stdc++.h>
using namespace std;
const int N=1e4, M=1e4;
int head[N],vis[N],dis[N],tot,n,m;//head是表头(head[i]表示i起点的边号),vis表示该点是否已在队列中,为了防止同个点重复入队
struct node{int to,w,next;} e[M];
void add(int u,int v,int w){e[++tot]=(node){v,w,head[u]};head[u]=tot;}
void spfa(int t){queue<int> q;memset(dis,0x3f,sizeof(dis));dis[t]=0; vis[t]=1; //注意vis等于1表示队列中已经存在此点q.push(t);while(!q.empty()){int cur=q.front(); q.pop();vis[cur]=0;//扩展后此点出队for(int i=head[cur];i;i=e[i].next){//i是边号 遍历点cur连向的周围边i的点vint v=e[i].to,w=e[i].w;if(dis[v]>dis[cur]+w){//判断是否需要更新,更新过的且不在队伍的点才入队,方便找更优解dis[v]=dis[cur]+w;if(!vis[v])q.push(v),vis[v]=1;}}}
}
int main(){int n,m,t;cin>>n>>m>>t;for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;add(u,v,w);}spfa(t);for(int i=1;i<=n;i++){cout<<dis[i]<<" ";}return 0;
}
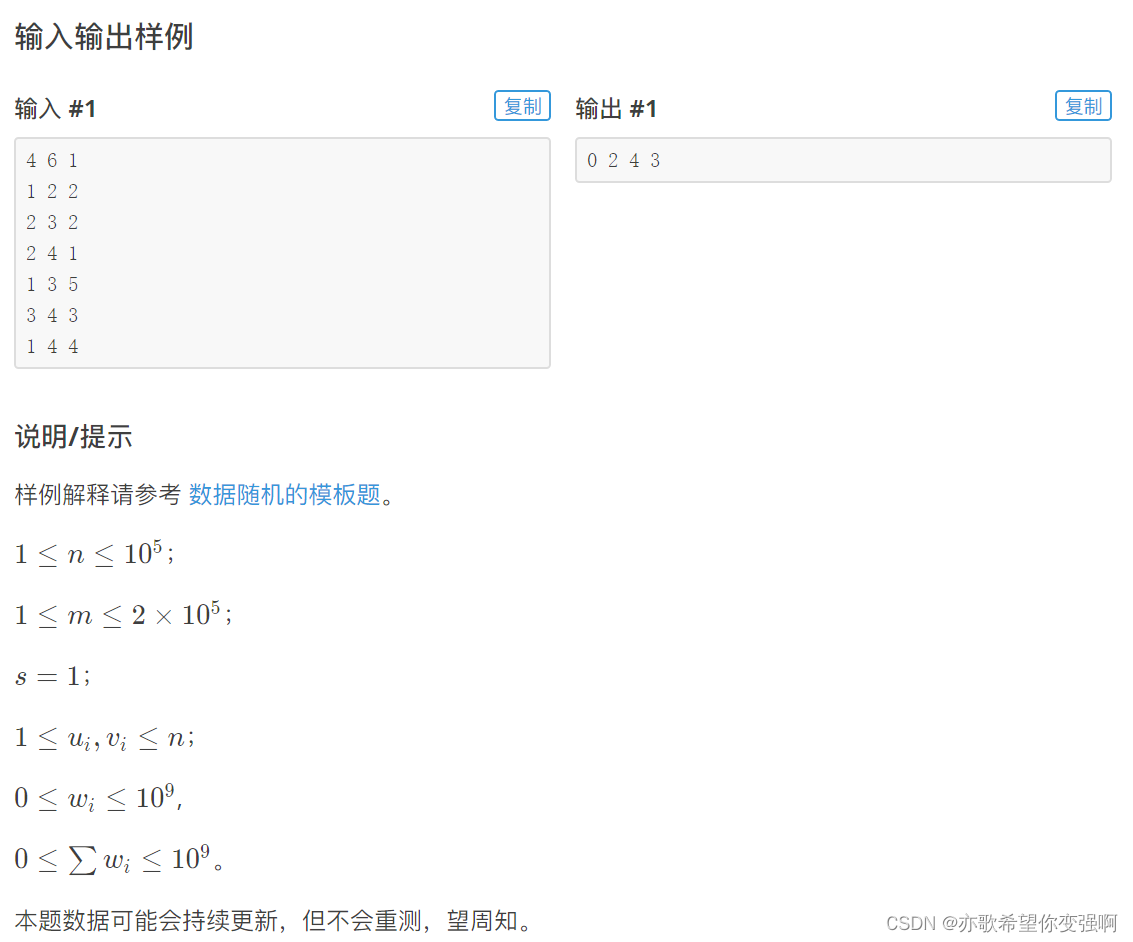
题目:我们把上百件衣服从商店运回赛场,求最短的从上商店到赛场的路线
输入:第一行N(<=100),M(<=10000),N表示有几个路口(1号路口是商场所在地,n号是赛场)M表示有几条路,N=M=0时输入结束,接下来M行每行包括A,B,C表示A,B两口路需要耗时C时间
输出:对每组输入,输出一行,表示工作人员从商店到赛场的最短时间
样例: 2 1 输出:3
1 2 3 2
3 3
1 2 5
2 3 5
3 1 2
0 0
#include <bits/stdc++.h>
using namespace std;
const int N=1e4+10;
const int M=1e4+10;
long long dis[N],u[N],v[N],w[N];//按边初始化无向图
int n,m,cnt;
long long ans;
long long bellman_fold(int s,int t){memset(dis,0x3f,sizeof(dis));//初始化无穷大dis[s]=0;for(int i=1;i<=n-1;i++){//最多松弛n-1次int check=0;//是否可以提前结束松弛for(int j=1;j<=cnt;j++){//对每条边进行松弛,更新disif(dis[u[j]]+w[j]<dis[v[j]]){dis[v[j]]=dis[u[j]]+w[j];check=1;}}if(check==0)break;}return dis[t];
}
int main(){while((cin>>n>>m)&&(n+m)){cnt=1;for(int i=1;i<=m;i++){//初始化无向图(按边),因为只需要用到每条边,所有初始化只需要按边初始化即可int x,y,z;cin>>x>>y>>z;u[cnt]=x;v[cnt]=y;w[cnt]=z;//w表示每条边的长度,u表示对应边的起点,v表示对边的终点,这样方便对每条边访问cnt++;u[cnt]=y;v[cnt]=x;w[cnt]=z;cnt++;}ans=bellman_fold(1,n);cout<<ans<<endl;}
}不过bellman我不怎么用,只是给出来一下。
相关文章:

【算法每日一练]-图论(保姆级教程 篇1(模板篇)) #floyed算法 #dijkstra算法 #spfa算法
今天开始讲图论 目录 图的存储 算任意两点的最短路径: floyed算法: 算一个点到其他所有点的最短距离 dijkstra算法: spfa算法: 图的存储 其实:邻接矩阵和链式向前星都能存边的信息,vector只能存点的信息,再搭配上v[]…...

c语言数据结构---十字链表
#include<stdio.h> #include<stdlib.h> typedef struct node{//十字链表 输入三元组返回矩阵 int row,col,val;struct node *down,*right; }JD,*J; typedef struct {J *rhead,*chead;int mu,nu,tu;//行列非0元 }CS; CS creat(CS M){int m,n,t;;int k,j,e;JD *p,*q…...
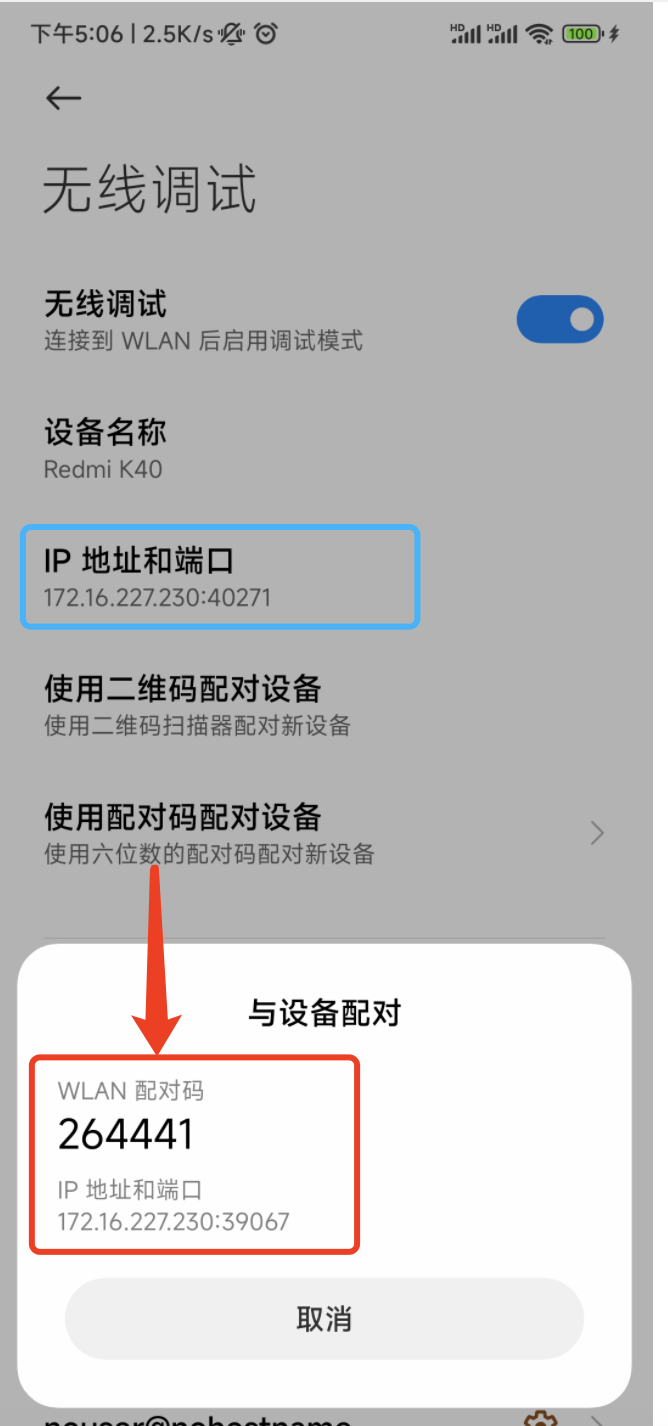
使用python电脑轻量级控制手机—adb命令和手机投屏
文章目录 一、通过无线连接手机和电脑二、使用adb命令轻量级控制手机二、使用scrcpy控制手机 通过电脑控制手机有多种方式如appnium等,本文介绍的是两种轻量级的方案,使用adb命令刚和手机投屏。 一、通过无线连接手机和电脑 1、手机设置 开发者选项—us…...

VBA技术资料MF82:替换文件夹中文件名中的字符
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…...
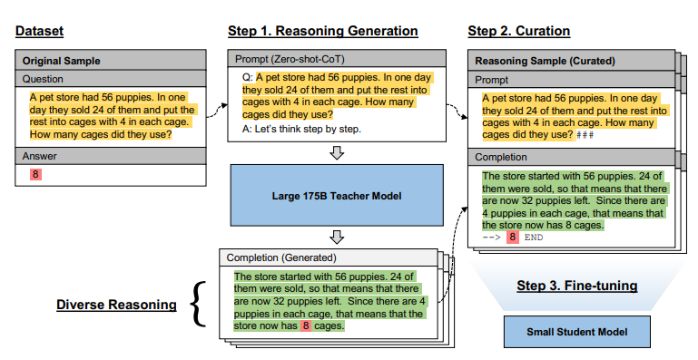
如何利用大模型蒸馏出小模型实现降本
如何让小模型的推理效果在某些领域比 ChatGPT 这样的大模型还要更强?这篇论文提供了一个思路:https://arxiv.org/abs/2212.10071,借助思维链(CoT)逐步解决复杂推理任务的能力,可以使用大模型作为推理教师&a…...

CentOS 中启动 Jar 包
在 CentOS 中启动一个 Jar 包,可以通过 java 命令来实现。具体步骤如下: 确认 Java 环境已经安装并配置好了。 打开终端或者 SSH 连接到 CentOS 服务器。 执行以下命令启动 Jar 包: 复制插入 java -jar /path/to/your/jar/file.jar复制插…...

法治智能起航 | 拓世法宝AI智慧政务一体机重塑法治格局,开启智能司法新篇章
在科技的巨轮推动下,我们的社会正快速迈向一个以数据和智能为核心的新时代。在这个波澜壮阔的变革中,人工智能(AI)显得尤为突出,它不仅是科技进步的象征,更是未来发展的助力者。 2023年,最高人…...
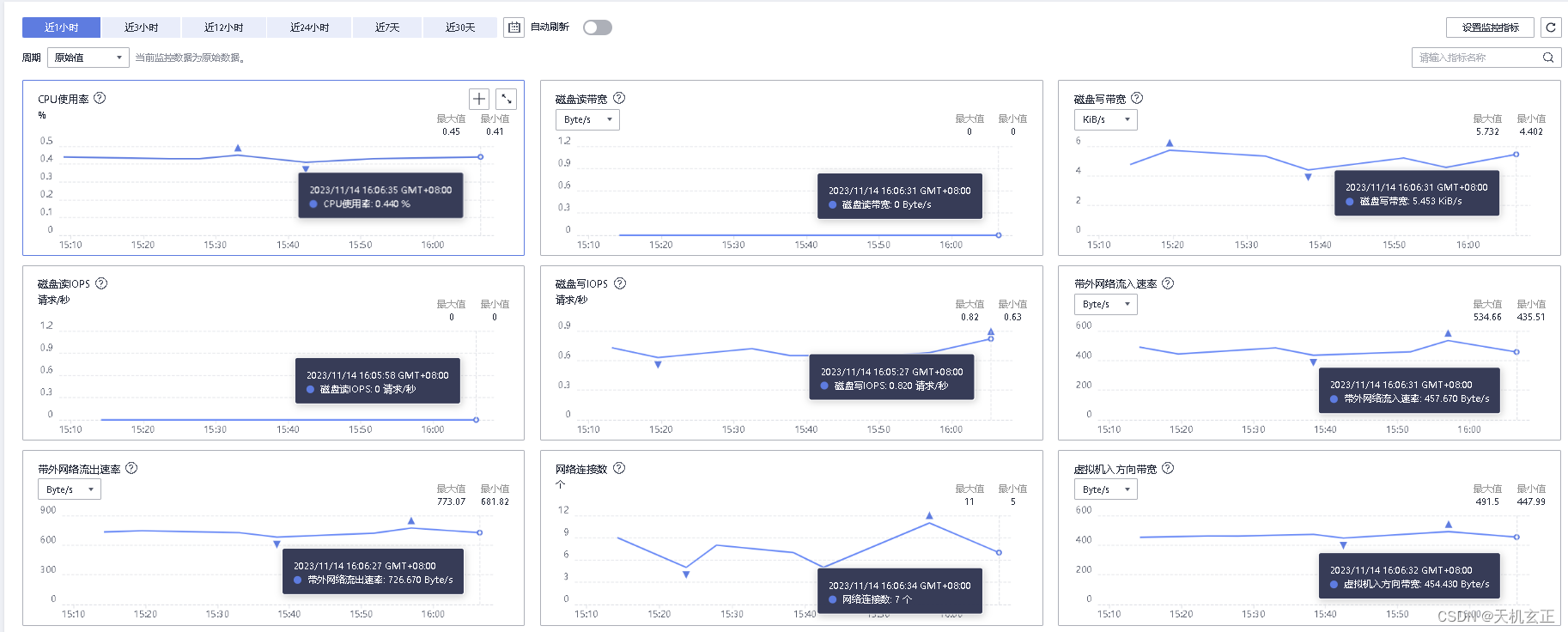
【华为云IaaS基础三件套之----计算ECS、网络EIP、存储EVS】
MD[华为云IaaS基础三件套----计算、网络、存储] 华为云IaaS基础三件套之----计算ECS、网络EIP、存储EVS 说明: 这里只是简单从计算/网络/存储,进行介绍,阐明云上对于云下的优势;因ECS是三者综合,故最后说明。 1.网络----弹性公…...

c语言数据结构---广义表
#include<stdio.h> #include<stdlib.h> typedef struct GNode{//广义表 int NodeTag; //标志域union{ char data;struct GNode *sublist;};struct GNode *next; }*PGNode,PG; void CreateGList(PGNode &GL) {char ch;scanf("%c", …...

2023.11.12使用flask对图片进行黑白处理(base64编码方式传输)
2023.11.12使用flask对图片进行黑白处理(base64编码方式传输) 由前端输入图片并预览,在后端处理图片后返回前端显示,可以作为图片处理的模板。 关键点在于对图片进行base64编码的转化。 使用Base64编码可以更方便地将图片数据嵌入…...
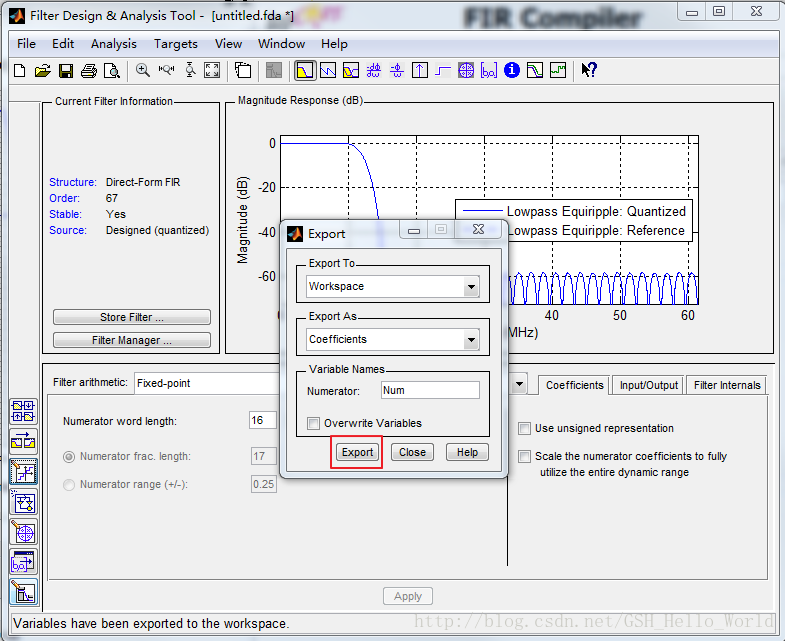
MATLAB中Filter Designer的使用以及XILINX Coefficient(.coe)File的导出
文章目录 Filter Designer的打开滤波器参数设置生成matlab代码生成XILINX Coefficient(.COE) File实际浮点数的导出官方使用教程 Filter Designer的打开 打开Filter Designer: 方法一:命令行中输入Filter Designer,再回车打开。 方法二&…...
)
js 深度学习(四)
函数 var test function test1(){var a 1,b2console.log(a,b)test1()//递归 } console.log(test.name) //test1 test1() //报错匿名函数表达式 函数自变量 var test function(){->匿名函数var a 1,b2console.log(a,b)test1()//递归 }var test function(a,b){var a 1,b2…...
leetcode刷题日记:121. Best Time to Buy and Sell Stock( 买卖股票的最佳时机)
题目给了我们一组数prices,其中prices[i]表示第i天的股票价格,需要我们求出买卖股票所能获得的最大收益。 我们的第一想法就是从算出每一种买卖股票的情况然后求出里面的最大值,这样我们就能得到最大收益是多少,但是这种情况过于复…...
Mac 本地部署thinkphp8【部署环境以及下载thinkphp】
PHP的安装以及环境变量配置 1 PHP安装:在终端输入brew install php 这里是PHP下载的最新的 如果提示‘brew’找不到,自己搜索安装吧, 不是特别难 2 环境变量配置 终端输入vim ~/.bash_profile 输入export PATH"/usr/local/Cellar/php/8.…...
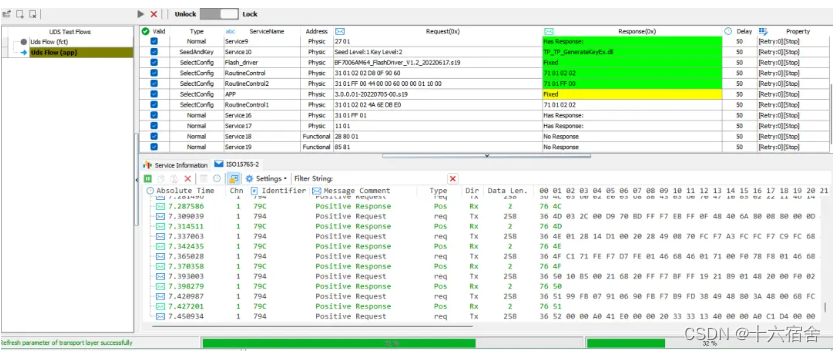
【汽车电子】CAN总线分析仪使用介绍(PCAN/同星CAN卡)
本篇文章以CAN卡的使用为基本线索,介绍了在汽车电子领域涉及的一些CAN卡使用流程,搭配强大的上位机可以实现诸多功能。文章并没有局限于一种CAN卡,而是针对PCAN和同星的CAN卡分别以常用CAN报文收发以及诊断控制台实现这两种方向进行了CAN卡使…...

C //例 7.13 有一个3*4的矩阵,求所有元素中的最大值。
C程序设计 (第四版) 谭浩强 例 7.13 例 7.13 有一个3*4的矩阵,求所有元素中的最大值。 IDE工具:VS2010 Note: 使用不同的IDE工具可能有部分差异。 代码块 方法:使用指针、动态分配内存 #include <stdio.h> …...
基于SSM的供电所档案管理系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...
excel用RAND函数生成一个大于0小于1的随机数
插入-》函数: 选择RAND函数: 点击“继续”: 点击“确定”,就生成随机数了:...
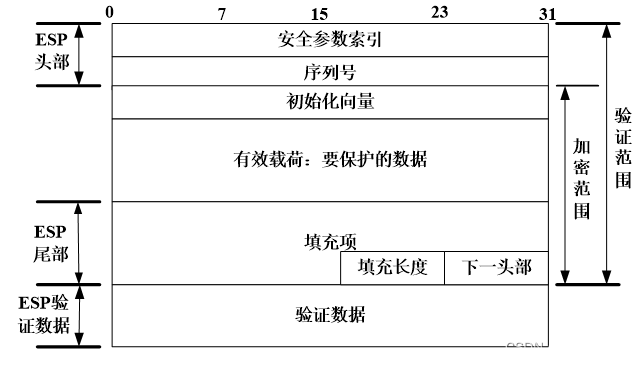
详解IP安全:IPSec协议簇 | AH协议 | ESP协议 | IKE协议
目录 IP安全概述 IPSec协议簇 IPSec的实现方式 AH(Authentication Header,认证头) ESP(Encapsulating Security Payload,封装安全载荷) IKE(Internet Key Exchange,因特网密钥…...

mysql使用--数据库的基本操作
在MYSQL中,一些表的集合称为一个数据库。MYSQL服务器管理若干个数据库,每个数据库下都可有若干个表。 1.展示数据库 SHOW DATABASES; 2.创建数据库 如:CREATE DATABASE myname; 更智能语法,可用:CREATE DATABASE IF …...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...
