算法分析与设计考前冲刺 (算法基础、数据结构与STL、递归和分治、 动态规划、贪心算法、 回溯算法)
算法分析与设计考前冲刺
算法基础
算法是一系列解决问题的清晰指令,代表着用系统的方法描述解决问题的策略机制。
程序是算法用某种程序设计语言的具体的 具体实现
算法特征: 有穷性(有限步) 确定性 输入 输出 可行性(有限时间)
算法的复杂性: 时间复杂性 和空间复杂性(算法消耗的内存空间)
数据结构与STL
栈: 先进后出
向量: 动态数组,可以随机存储
Map: 有key和value 底层是红黑树,按照key自动进行排序
list: 线性链表
set: 内部元素不允许重复
队列: 先进先出
优先队列:最大的元素位于队首 ,最大的元素优先出队
递归和分治
分治:原问题可以拆分为多个子问题,子问题之间相互独立且 与 原问题形式相同
分治步骤: 分解 解决 合并
Fab数列:
int fib(int n) //声明一个函数fib,它接受一个整数参数n,并返回一个整数。
{ if (n<=1) return 1;return fib(n-1)+fib(n-2);
}
int fib[50];
void fibonacci(int n) //定义了一个名为 fibonacci 的函数,它接受一个整数参数 n
{fib[0] = 1;fib[1] = 1; for (int i=2; i<=n; i++)fib[i] = fib[i-1]+fib[i-2]; }
二分:
int BinarySearch(Type a[],const Type& x,int n)
{int left=0; int right=n-1; while(left<=right)//左闭右闭{int middle=(left+right)>>1;if (x==a[middle]) return middle; if (x>a[middle]) left=middle+1; else right=middle-1; }
return -1; //如果循环结束后仍然没有找到目标元素
} 二分:
int BinarySearch(Type a[],const Type& x,int n)
{int left=0; int right=n; while(left<right)//左闭右开{int middle=(left+right)>>1;if (x==a[middle]) return middle; if (x>a[middle]) left=middle+1; //middle已经判断不是了else right=middle; //不-1 因为是左闭右开 }
return -1; //如果循环结束后仍然没有找到目标元素
}
动态规划:
场景:通常用与求解具有某种 最优性质 的问题
思想:是将待求解问题分解成若干个 不独立的子问题 ,先求解子问题,将子问题的答案记录在表格
步骤:
- 找出最优解的性质,并刻画其结构特征;
- 确定状态转移方程
- 以自底向上的方式计算出最优值;
- 根据计算最优值时得到的信息,构造一个最优解。
性质: 最优子结构 重叠子问题
0-1背包:
解法一:
#include<iostream>
#include<algorithm>
using namespace std;
const int M=1010;
int w[M],v[M];
int dp[M][M];
int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){ //两层循环都正序遍历 因为dp[i][j] 是由上面的元素和左上方得到的dp[i][j]=dp[i-1][j];//表示不选择第i键物品if (j>=v[i]){//当背包容量大于物品体积的时候取最大值dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);}}}cout<<dp[n][m]<<endl;return 0;
}解法二:
#include<iostream>
#include<algorithm>
#include <cstdio>
using namespace std;
const int M=1010;
const int N=1e6+10;
int w[M],v[M];
int dp[M];int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=m;j>=v[i];j--){//倒序遍历不然会存在覆盖的问题dp[j]=max(dp[j],dp[j-v[i]]+w[i]);}}cout<<dp[m]<<endl;return 0;}贪心算法
场景:只考虑当前最好的选择,讲原问题化成一个更小的与原问题具有相同形式的子问题
特点:只考虑局部最优,不从整体最优考虑
最优解有的适合可能是很好的一个近似解
选硬币:
现有面值分别为1角1分,5分,1分的硬币,请给出找1角5分钱的最佳方案。
#include <iostream>
#include <vector>std::vector<int> findChange(int amount) {std::vector<int> coins = {10, 5, 1}; // 按面值从大到小排序的硬币面值std::vector<int> result(coins.size(), 0); // 用于存储每种硬币的数量for (int i = 0; i < coins.size(); i++) {int numCoins = amount / coins[i]; // 计算当前硬币面值的数量result[i] = numCoins; // 存储数量amount -= numCoins * coins[i]; // 更新剩余金额}return result;
}int main() {int amount = 15; // 需要找零的金额,单位为分std::vector<int> change = findChange(amount);std::cout << "找零方案为:" << std::endl;std::cout << "1角1分硬币数量:" << change[0] << std::endl;std::cout << "5分硬币数量:" << change[1] << std::endl;std::cout << "1分硬币数量:" << change[2] << std::endl;return 0;
}
思路:不需要想的很清楚,想一下生活中的找钱,如果别人给你100元,花了15元,你应该是先找给他50元然后在其20 10 5,(这里默认每一种都有无数张),这就是一个贪心,贪心贪在你每次都找给他最大的,可能这个还是不是很好理解,就是1元可以给任何钱找钱,而50元只有大于50元我才可以找找,很多时候无形之中就已经使用了贪心。
背包问题:
下面是贪心做法:
//形参n是物品的数量,c是背包的容量M,数组a是按物品的性价比降序排序
double knapsack(int n, bag a[], double c)
{double cleft = c; //背包的剩余容量int i = 0;//下标double b = 0; //获得的价值//当背包还能完全装入物品iwhile(i <n && a[i].w<cleft) //这里的a[i]是一个结构体数组 元素包括重量、价值即(v,w,性价比){cleft -= a[i].w;b += a[i].v;i++;}// 物品可拆分 a[i].v/a[i].w 是i物品的单位价值if (i<n) b += 1.0*a[i].v*cleft/a[i].w;//凑满背包
return b;
}
总结:背包问题贪心贪在,你优先按照性价比降序排列,每次优先考虑价值最高的物品
回溯算法
核心:组织搜索 搜索一个问题的所有解
思想:
- 用约束函数在扩展结点处减去不满足约束条件的子树;
- 用限界函数减去不能得到最优解的子树。
素数环问题:
素数环,从1到20这20个数摆成一个环,要求相邻的两个数的和是一个素数。
//判断质数
bool pd(int x,int y){int k=2,i=x+y;while (k<=sqrt(i)&&i%k!=0) k++; //if (k>sqrt(i)) return true;//遍历半圈没有找到else return false;//前面能被整除
}
void search(int t){ int i;for (i=1;i<=20;i++) if (pd(a[t-1],i)&&(!b[i])){ //判断当前数和前一位的和是不是素数同时 当前元素没有出现过a[t]=i; //放入b[i]=1; //出现一次if (t==20) {
if (pd(a[20],a[1])) print(); }//注意边界 最后一个和第一个是连着的else
search(t+1); //递归寻找下一个数字b[i]=0;//回溯}
}
int print(){total++;cout<<"<"<<total<<">";for (int j=1;j<=20;j++)cout<<a[j]<<" ";cout<<endl; }
相关文章:
)
算法分析与设计考前冲刺 (算法基础、数据结构与STL、递归和分治、 动态规划、贪心算法、 回溯算法)
算法分析与设计考前冲刺 算法基础 算法是一系列解决问题的清晰指令,代表着用系统的方法描述解决问题的策略机制。 程序是算法用某种程序设计语言的具体的 具体实现 算法特征: 有穷性(有限步) 确定性 输入 输出 可行性(有限时间) 算法的复杂性&#…...

Spring Data JPA 实现集成实体对象数据库的创建、修改时间字段自动更新
JPA提供了一种事件监听器的机制,用于SQL审计,通过监听器我们可以很快速地去自动更新创建时间、修改时间,主要步骤如下: 一、创建基础实体,包含了创建和修改时间,然后让其他真正的实体继承该实体࿰…...

Vue3集成json-editor-vue3
安装依赖 npm install json-editor-vue3 --save引入 main.js import "jsoneditor";具体模块 import JsonEditorVue from json-editor-vue3;代码实现 <json-editor-vue ref"jsonEditor" class"editor" v-model"state.addFormField.p…...

UML建模语言
UML建模语言 类的关系 依赖关系 类的方法中使用形参、局部变量或者静态方法的方式调用其他类,表示当前类依赖其他类。 public class Main {public void eat(Person person) {person.play();// 方法参数Student student new Student();student.study();// 局部变…...
centos7系统离线安装tcpdump抓包软件、使用教程
tcpdump 是Linux系统下的一个强大的命令,可以将网络中传送的数据包完全截获下来提供分析。它支持针对网络层、协议、主机、网络或端口的过滤,并提供and、or、not等逻辑语句来帮助你去掉无用的信息。 本教程对tcpdump命令使用进行讲解说明,通…...
划分VOC数据集,以及转换为划分后的COCO数据集格式
1.VOC数据集 LabelImg是一款广泛应用于图像标注的开源工具,主要用于构建目标检测模型所需的数据集。Visual Object Classes(VOC)数据集作为一种常见的目标检测数据集,通过labelimg工具在图像中标注边界框和类别标签,为…...

JAVA基础8:方法
1.方法概念 方法(method):将具有独立功能的代码块组织成为一个整体,使其具有特殊功能的代码集。 注意事项: 方法必须先创建才可以使用,该过程称为方法定义方法创建后并不是直接运行的,需要手动使用后才执…...

域名反查Api接口——让您轻松查询域名相关信息
在互联网发展的今天,域名作为网站的唯一标识符,已经成为了企业和个人网络营销中不可或缺的一部分。为了方便用户查询所需的域名信息,API接口应运而生。本文将介绍如何使用挖数据平台《域名反查Api接口——让您轻松查询域名相关信息》进行域名…...
果儿科技:打造无代码开发的电商平台、CRM和用户运营系统
连接业务系统:果儿科技与集简云的无代码开发 北京果儿科技有限公司,自2015年成立以来,始终专注于研发创新的企业服务解决方案。其中,集简云无代码集成平台是我们的一项杰出成果,它实现了与近千款软件系统的连接&#…...

C++ 并发编程中condition_variable和future的区别
std::condition_variable 和 std::future 的区别: 用途不同: std::condition_variable: 就好比是一把魔法门,有两个小朋友,一个在门这边,一个在门那边。门上贴了一张纸,写着“开心时可以进来…...
【保姆级教程】Linux安装JDK8
本文以centos7为例,一步一步进行jdk1.8的安装。 1. 下载安装 官网下载链接: https://www.oracle.com/cn/java/technologies/downloads/#java8 上传jdk的压缩包到服务器的/usr/local目录下 在当前目录解压jdk压缩包,如果是其它版本…...
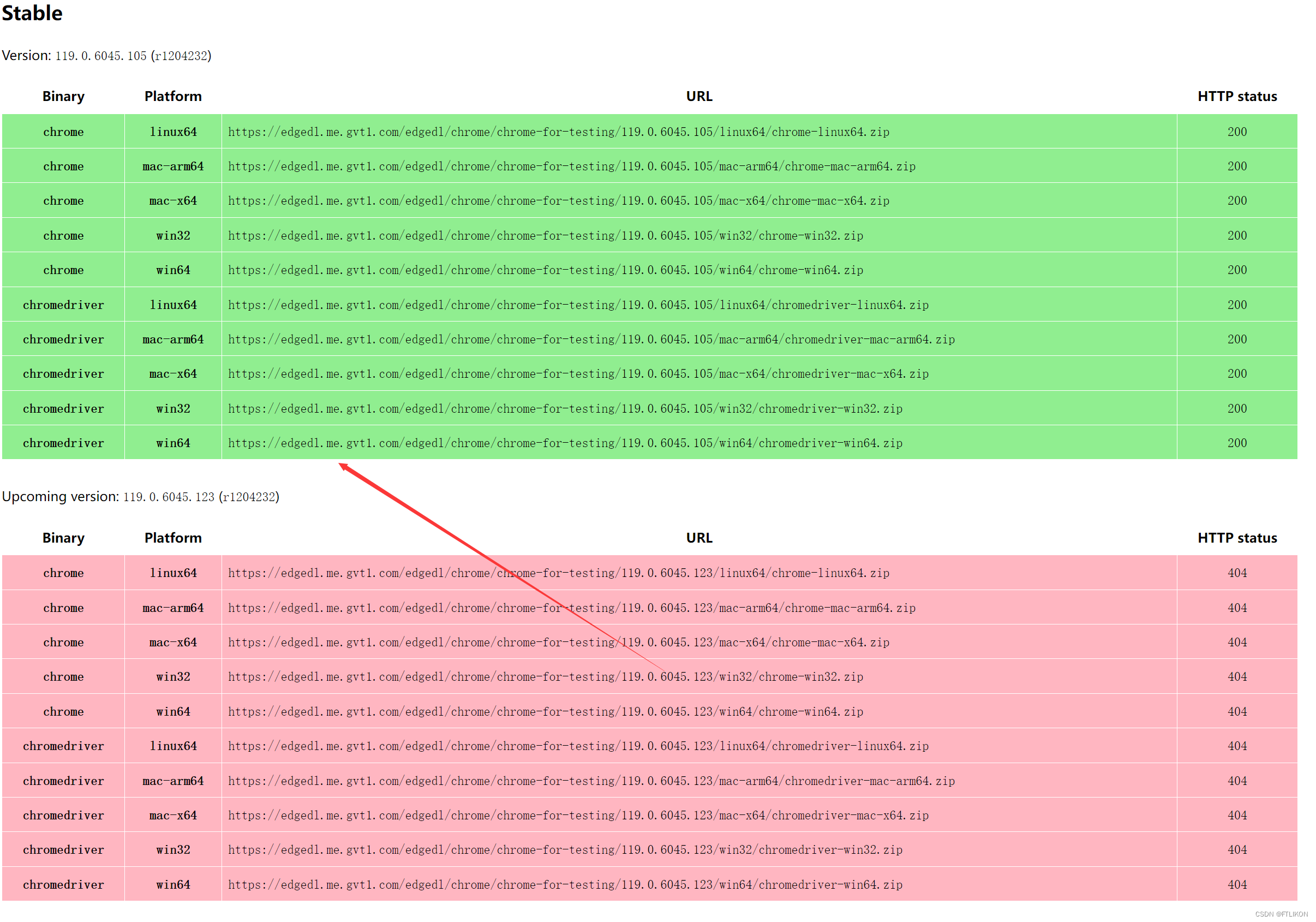
【备忘】ChromeDriver 官方下载地址 Selenium,pyppetter依赖
https://googlechromelabs.github.io/chrome-for-testing/#stable windows系统选择win64版本下载即可...

day08_osi各层协议,子网掩码,ip地址组成与分类
osi各层协议,子网掩码,ip地址组成与分类 一、上节课复习二 今日内容:1、子网划分 来源于http://egonlin.com/。林海峰老师课件 一、上节课复习 1、osi七层与数据传输 2、socketsocket是对传输层以下的封装ipport标识唯一一个基于网络通讯的软件3、tcp与…...
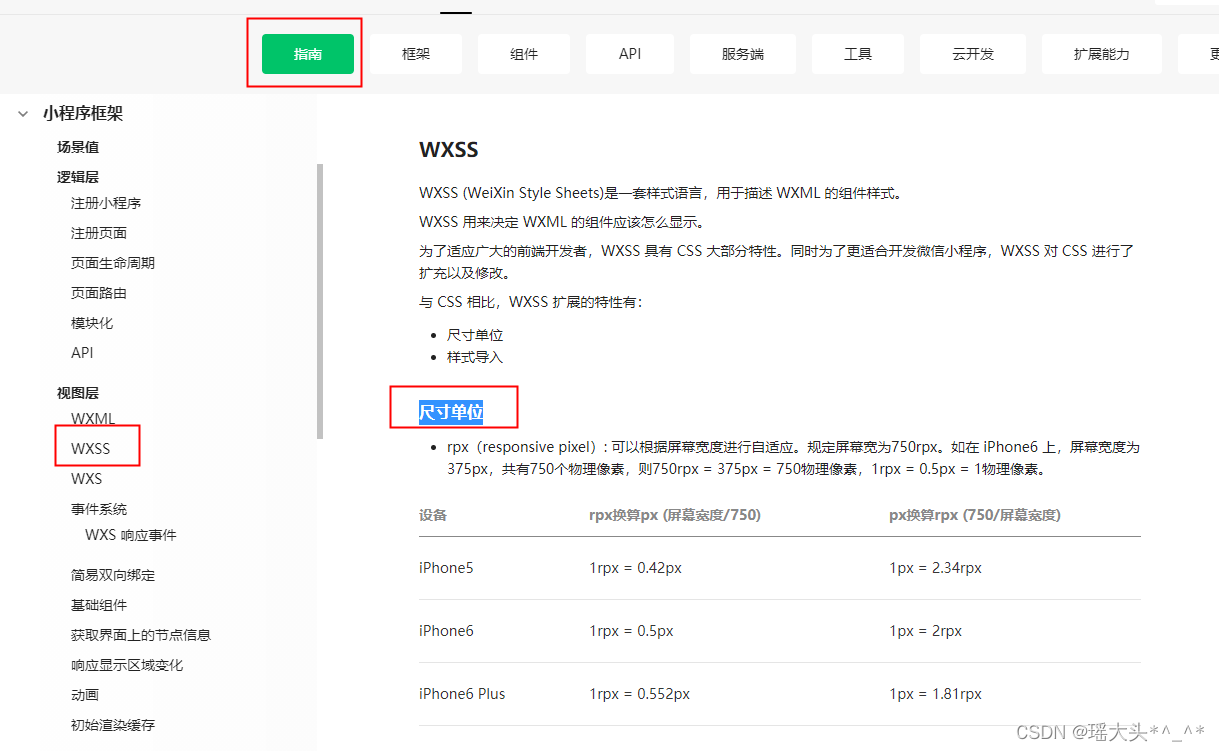
微信小程序:tabbar、事件绑定、数据绑定、模块化、模板语法、尺寸单位
目录 1. tabbar 1.1 什么是tabbar 1.2 配置tabbar 2. 事件绑定 2.1 准备表单 2.2 事件绑定 2.3 冒泡事件及非冒泡事件 3. 数据绑定 3.1 官方文档 4. 关于模块化 5. 模板语法 6. 尺寸单位 1. tabbar 1.1 什么是tabbar 下图中标记出来的部分即为tabbar:…...

AR工业眼镜:智能化生产新时代的引领者!!
科技飞速发展,人工智能与增强现实(AR)技术结合正在改变生活工作方式。AR工业眼镜在生产领域应用广泛,具有实时信息展示、智能导航定位、远程协作培训、智能安全监测等功能,提高生产效率、降低操作风险,为企…...

从0到0.01入门React | 008.精选 React 面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…...
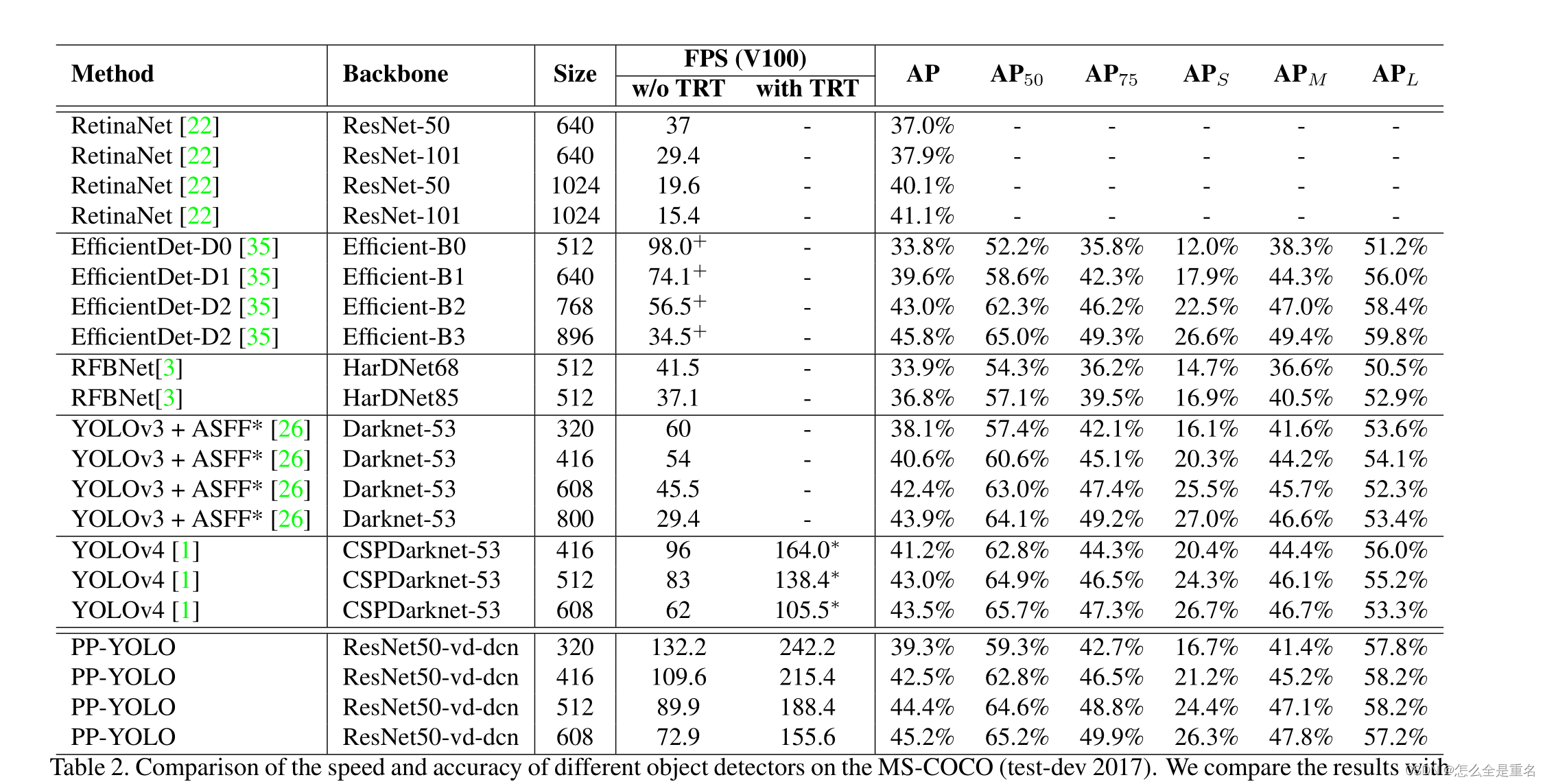
PP-YOLO: An Effective and Efficient Implementation of Object Detector(2020.8)
文章目录 Abstract1. Introduction先介绍了一堆前人的work自己的workexpect 2. Related Work先介绍别人的work与我们的区别 3.Method3.1. ArchitectureBackboneDetection NeckDetection Head 3.2. Selection of TricksLarger Batch SizeEMADropBlockIoULossIoU AwareGrid Sensi…...
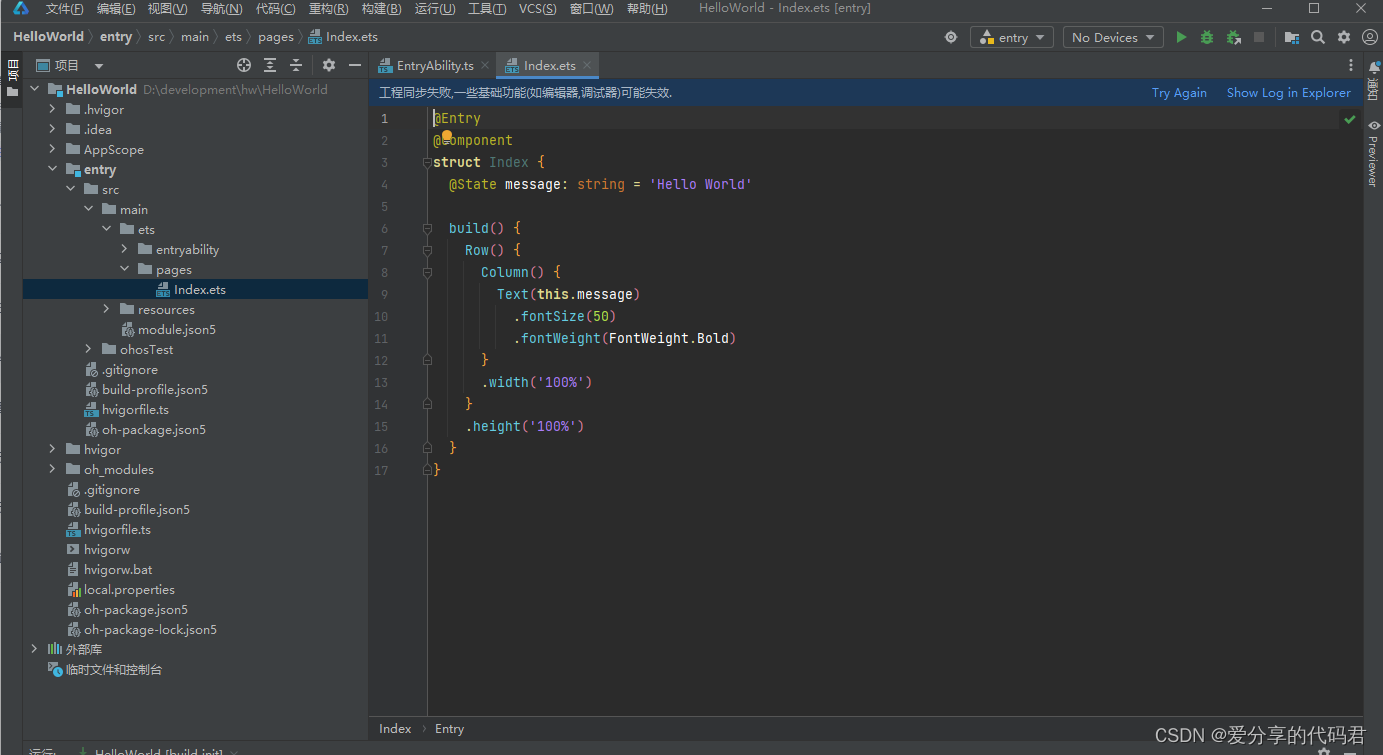
4、创建第一个鸿蒙应用
一、创建项目 此处以空模板为例来创建一个鸿蒙应用。在创建项目前请保持网页的畅通。 1、在欢迎页面点击“Create Project”。 2、左侧默认为“Application”,在“Template Market”中选择空模板(Empty Ability),点击“Next” 3…...

Docker - DockerFile
Docker - DockerFile DockerFile 描述 dockerfile 是用来构建docker镜像的文件!命令参数脚本! 构建步骤: 编写一个dockerfile 文件docker build 构建成为一个镜像docker run 运行脚本docker push 发布镜像(dockerhub࿰…...

2311rust模式匹配
原文 在Rust中混合匹配,改变和移动 结构模式匹配:极大的改进了C或Java风格的switch语句. Match包含命令式和函数式编程风格:可继续使用break语句,赋值等,不必面向表达式. 按需匹配"借用"或"移动",:Rust鼓励开发者仔细考虑所有权和借用.设计匹配时仅支持…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
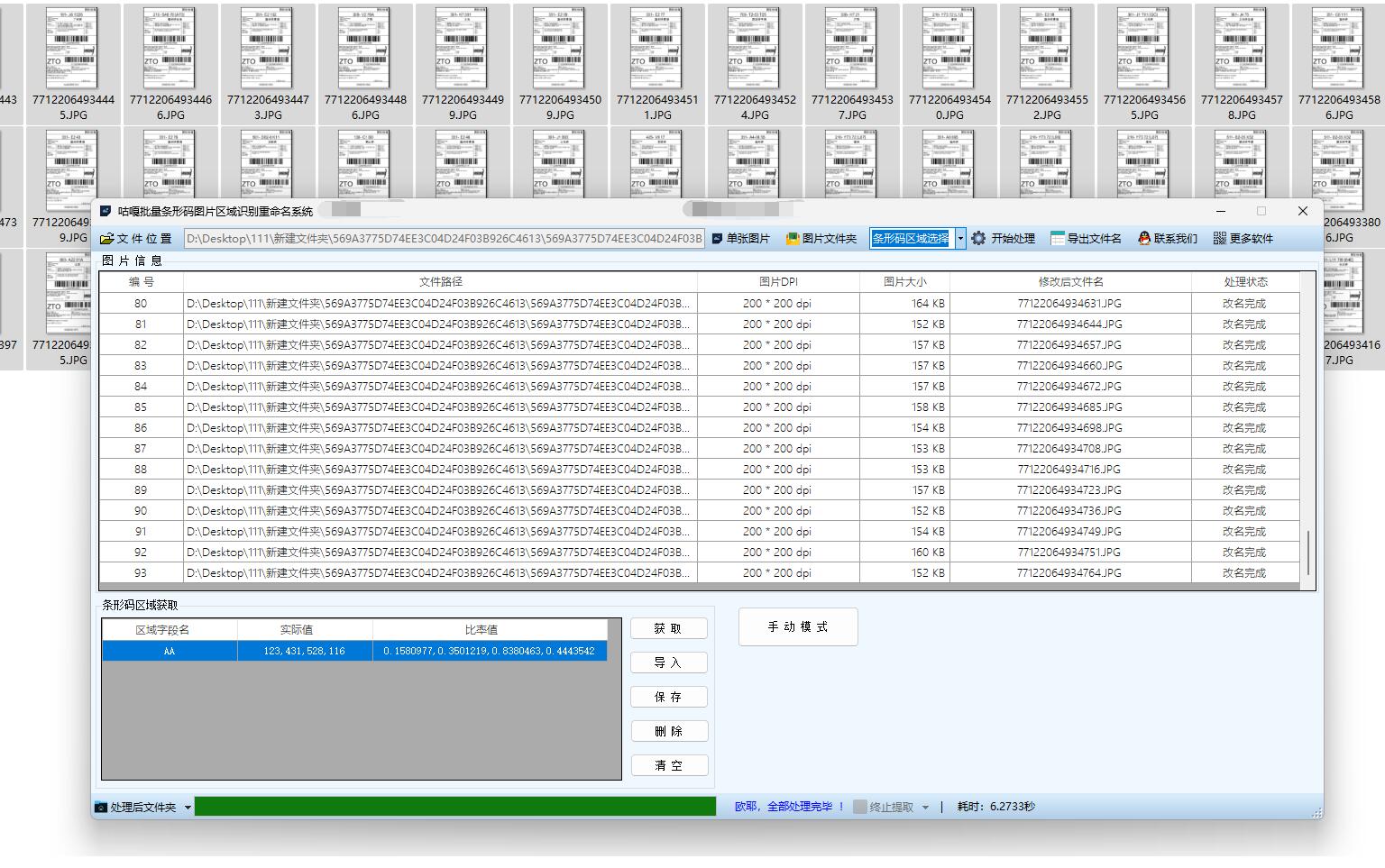
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...
