深度学习优化算法总结
深度学习的优化算法
-
优化的目标
优化提供了一种最大程度减少深度学习损失函数的方法,但本质上,优化和深度学习的目标不同。
优化关注的是最小化目标;深度学习是在给定有限数据量的情况下寻找合适的模型。
-
优化算法
-
gradient descent(梯度下降)
考虑一类连续可微实值函数f:R→Rf:\mathbb{R} \rightarrow \mathbb{R}f:R→R,利用泰勒展开,可以得到:
f(x+ϵ)=f(x)+ϵf′(x)+O(ϵ2)f(x + \epsilon ) = f(x) + \epsilon f'(x) + O(\epsilon ^2) f(x+ϵ)=f(x)+ϵf′(x)+O(ϵ2)
在一阶近似中,f(x+ϵ)f(x + \epsilon )f(x+ϵ) 可通过xxx处的函数值f(x)f(x)f(x)和一阶导数f′(x)f'(x)f′(x)得出。假设在负梯度方向上移动的ϵ\epsilonϵ会减少fff。为了简化问题,选择固定步长η>0\eta > 0η>0,然后取ϵ=−ηf′(x)\epsilon = - \eta f'(x)ϵ=−ηf′(x),将其带入泰勒展开式后,得到
f(x−ηf′(x))=f(x)−ηf′2(x)+O(η2f′2(x))f(x - \eta f'(x)) = f(x) - \eta f'^2(x) + O(\eta^2f'^2(x)) f(x−ηf′(x))=f(x)−ηf′2(x)+O(η2f′2(x))
若f′(x)≠0f'(x) \ne 0f′(x)=0,则ηf′2(x)>0\eta f'^2(x) > 0ηf′2(x)>0。另外,总是可以找到令η\etaη足够小使得高阶项变的不相关,因此
f(x−ηf′(x))<f(x)f(x - \eta f'(x)) < f(x) f(x−ηf′(x))<f(x)
这意味着,如果使用
x←x−ηf′(x)x \leftarrow x - \eta f'(x) x←x−ηf′(x)
来迭代x,函数f(x)f(x)f(x)的值可能会下降。因此,在梯度下降中,首先选用初始值xxx和η>0\eta > 0η>0,然后使用它们连续迭代xxx,直到停止条件达成。例如:当梯度∣f′(x)∣|f'(x)|∣f′(x)∣的幅度足够小或迭代次数达到某个值。
其中,步长η\etaη叫做学习率,是超参数,其决定目标函数能否收敛到局部最小值,以及何时收敛到最小值。
-
SGD(随机梯度下降)
深度学习中,目标函数通常是训练数据集中每个样本的损失函数的平均值。
给定nnn个样本,假设fi(x)f_i(x)fi(x)是关于索引iii的训练样本的损失函数,其中XXX是参数向量,得到目标函数:
f(X)=1n∑i=1nfi(X)f(X) = \frac{1}{n} \sum_{i=1}^{n} f_i(X) f(X)=n1i=1∑nfi(X)
XXX的目标函数的梯度为:
∇f(X)=1n∑i=1n∇fi(X)\nabla f(X) = \frac{1}{n} \sum_{i=1}^{n} \nabla f_i(X) ∇f(X)=n1i=1∑n∇fi(X)
如果采用梯度下降法,每个自变量迭代的计算代价为O(n)O(n)O(n),其随nnn线性增长,因此,当训练数据集规模较大时,每次迭代的梯度下降的计算代价将更高。SGD可降低每次迭代时的计算代价。在随机梯度下降的每次迭代中,对数据样本随机均匀采样一个索引iii,其中i∈{1,...,n}i \in \{ 1,...,n \}i∈{1,...,n},并计算梯度∇fi(X)\nabla f_i(X)∇fi(X)来更新XXX:
x←x−η∇fi(X)x \leftarrow x - \eta \nabla f_i(X) x←x−η∇fi(X)
其中,η\etaη是学习率。可以发现,每次迭代的计算代价从梯度下降的O(n)O(n)O(n)下降到了常数O(1)O(1)O(1)。
此外,随机梯度∇fi(x)\nabla f_i(x)∇fi(x)是对完整梯度∇f(x)\nabla f(x)∇f(x)的无偏估计。
E∇fi(X)=1n∑i=1n∇fi(X)=∇f(X)\mathbb{E} \nabla f_i(X) = \frac{1}{n} \sum_{i=1}^{n} \nabla f_i(X) = \nabla f(X) E∇fi(X)=n1i=1∑n∇fi(X)=∇f(X)
这意味着,平均而言,随机梯度是对梯度的良好估计。 -
minibatch-SGD(小批量随机梯度下降)
处理单个观测值需要我们执行许多单一矩阵-矢量(甚至矢量-矢量)乘法,这耗费很大,而且对应深度学习框架也要巨大的开销。这既适用于计算梯度以更新参数时,也适用于用神经网络预测。既,当执行w←w−ηtgt\mathbf{w} \leftarrow \mathbf{w} - \eta_t \mathbf{g}_tw←w−ηtgt时,消耗巨大,其中:
gt=∂wf(xt,w).\mathbf{g}_t = \partial_{\mathbf{w}} f(\mathbf{x}_{t}, \mathbf{w}). gt=∂wf(xt,w).
可以通过将其应用于一个小批量观测值来提高次操作的计算效率。也就是说,将梯度gtg_tgt替换为一个小批量而不是单个观测值。
gt=∂w1∣Bt∣∑i∈Btf(xi,w).\mathbf{g}_t = \partial_{\mathbf{w}} \frac{1}{|\mathcal{B}_t|} \sum_{i \in \mathcal{B}_t} f(\mathbf{x}_{i}, \mathbf{w}). gt=∂w∣Bt∣1i∈Bt∑f(xi,w).
分析gt\mathbf{g}_tgt的统计属性的影响:- 梯度的期望保持不变:xt\mathbf{x}_txt和小批量Bt\mathcal{B}_tBt的所有元素都是从训练集中随机抽出的。
- 方差显著降低:小批量梯度由正在被平均计算的b:=∣Bt∣b := |\mathcal{B}_t|b:=∣Bt∣个独立梯度组成,其标准差降低了b−12b^{-\frac{1}{2}}b−21。
实践中我们选择一个足够大的小批量,它可以提供良好的计算效率同时仍适合GPU的内存。
-
momentum(动量法)
-
泄露平均值
在小批量随机梯度下降中,定义某次时间ttt的梯度下降计算公式:
gt,t−1=∂w1∣Bt∣∑i∈Btf(xi,wt−1)=1∣Bt∣∑i∈Bthi,t−1.\mathbf{g}_{t, t-1} = \partial_{\mathbf{w}} \frac{1}{|\mathcal{B}_t|} \sum_{i \in \mathcal{B}_t} f(\mathbf{x}_{i}, \mathbf{w}_{t-1}) = \frac{1}{|\mathcal{B}_t|} \sum_{i \in \mathcal{B}_t} \mathbf{h}_{i, t-1}. gt,t−1=∂w∣Bt∣1i∈Bt∑f(xi,wt−1)=∣Bt∣1i∈Bt∑hi,t−1.
小批量随机梯度下降可以作为加速计算的手段,同时其也有很好的副作用,即平均梯度减小了方差。
vt=βvt−1+gt,t−1\mathbf{v}_t = \beta \mathbf{v}_{t-1} + \mathbf{g}_{t, t-1} vt=βvt−1+gt,t−1
其中,β∈(0,1)\beta \in (0, 1)β∈(0,1)。这将有效的将瞬间梯度替换为“过去“多个梯度的平均值。v\mathbf{v}v被称为动量,其累加了过去的梯度。其中,可以vt\mathbf{v}_tvt扩展到
vt=β2vt−2+βgt−1,t−2+gt,t−1=…,=∑τ=0t−1βτgt−τ,t−τ−1.\begin{aligned} \mathbf{v}_t = \beta^2 \mathbf{v}_{t-2} + \beta \mathbf{g}_{t-1, t-2} + \mathbf{g}_{t, t-1} = \ldots, = \sum_{\tau = 0}^{t-1} \beta^{\tau} \mathbf{g}_{t-\tau, t-\tau-1}. \end{aligned} vt=β2vt−2+βgt−1,t−2+gt,t−1=…,=τ=0∑t−1βτgt−τ,t−τ−1.
其中,较大的β\betaβ相当于长期平均值,较小的β\betaβ相当于梯度只是略有修正。新的梯度替换不在指向模型中下降最陡的方向,而是指向过去梯度的加权平均值的方向。- 在优化问题不佳的情况下(例如函数某处”很平“,导数很小),具有动量的梯度可以借用之前的梯度来进行“加速”。
- 其允许我们对随后的梯度计算平均值,以获得更稳定的下降方向。
-
动量法
对于minibatch-SGD,使用vt\mathbf{v}_tvt而不是梯度gt\mathbf{g}_tgt可以生成以下更新等式:
vt←βvt−1+gt,t−1,xt←xt−1−ηtvt.\begin{aligned} \mathbf{v}_t &\leftarrow \beta \mathbf{v}_{t-1} + \mathbf{g}_{t, t-1}, \\ \mathbf{x}_t &\leftarrow \mathbf{x}_{t-1} - \eta_t \mathbf{v}_t. \end{aligned} vtxt←βvt−1+gt,t−1,←xt−1−ηtvt.
注意,对于β=0\beta = 0β=0,我们恢复常规的梯度下降。 -
有效样本权重
vt=∑τ=0t−1βτgt−τ,t−τ−1\mathbf{v}_t = \sum_{\tau = 0}^{t-1} \beta^{\tau} \mathbf{g}_{t-\tau, t-\tau-1}vt=∑τ=0t−1βτgt−τ,t−τ−1。极限条件下,∑τ=0∞βτ=11−β\sum_{\tau=0}^\infty \beta^\tau = \frac{1}{1-\beta}∑τ=0∞βτ=1−β1。
即,不同于在梯度下降或者随机梯度下降中取步长η\etaη,我们选取步长η1−β\frac{\eta}{1-\beta}1−βη,同时处理潜在表现可能会更好的下降方向。这是集两种好处于一身的做法。
-
小结:
-
动量法用过去梯度的平均值来替换梯度,这大大加快了收敛速度。
-
对于无噪声梯度下降和嘈杂随机梯度下降,动量法都是可取的。
-
动量法可以防止在随机梯度下降的优化过程停滞的问题。
-
由于对过去的数据进行了指数降权,有效梯度数为11−β\frac{1}{1-\beta}1−β1。
-
动量法的实现非常简单,但它需要我们存储额外的状态向量(动量v\mathbf{v}v)。
-
-
AdaGrad
-
稀疏特征和学习率
需要明确:为了使训练模型获得良好的准确性,我们大多希望在训练的过程中降低学习率,速度通常为O(t−12)\mathcal{O}(t^{-\frac{1}{2}})O(t−21)或更低。 对于稀疏特征(即只在偶尔出现的特征)的模型训练,只有在不常见的特征出现时,与其相关的参数才会得到有意义的更新。 鉴于学习率下降,我们可能最终会面临这样的情况:常见特征的参数相当迅速地收敛到最佳值,而对于不常见的特征,我们仍缺乏足够的观测以确定其最佳值。 换句话说,学习率要么对于常见特征而言降低太慢,要么对于不常见特征而言降低太快。
解决此问题的一个方法是记录我们看到特定特征的次数,然后将其用作调整学习率。 即我们可以使用大小为ηi=η0s(i,t)+c\eta_i = \frac{\eta_0}{\sqrt{s(i, t) + c}}ηi=s(i,t)+cη0的学习率,而不是η=η0t+c\eta = \frac{\eta_0}{\sqrt{t + c}}η=t+cη0。在这里s(i,t)s(i, t)s(i,t)计下了我们截至ttt时观察到功能iii的次数。
AdaGrad算法 通过将粗略的计数器s(i,t)s(i, t)s(i,t)替换为先前观察所得梯度的平方之和来解决这个问题。它使用s(i,t+1)=s(i,t)+(∂if(x))2s(i, t+1) = s(i, t) + \left(\partial_i f(\mathbf{x})\right)^2s(i,t+1)=s(i,t)+(∂if(x))2来调整学习率。
这有两个好处:
- 不再需要决定梯度何时算足够大。
- 其会随梯度的大小自动变化。通常对应于较大梯度的坐标会显著缩小,而其他梯度较小的坐标则会得到更平滑的处理。
-
AdaGrad算法:
使用变量st\mathbf{s}_tst来累加过去的梯度方差:
gt=∂wl(yt,f(xt,w)),st=st−1+gt2,wt=wt−1−ηst+ϵ⋅gt.\begin{aligned} \mathbf{g}_t & = \partial_{\mathbf{w}} l(y_t, f(\mathbf{x}_t, \mathbf{w})), \\ \mathbf{s}_t & = \mathbf{s}_{t-1} + \mathbf{g}_t^2, \\ \mathbf{w}_t & = \mathbf{w}_{t-1} - \frac{\eta}{\sqrt{\mathbf{s}_t + \epsilon}} \cdot \mathbf{g}_t. \end{aligned} gtstwt=∂wl(yt,f(xt,w)),=st−1+gt2,=wt−1−st+ϵη⋅gt.
η\etaη是学习率,ϵ\epsilonϵ是一个为维持数值稳定性而添加的常数,用来确保不会除以000。最后,初始化s0=0\mathbf{s}_0 = \mathbf{0}s0=0。就像在动量法中需要跟踪一个辅助变量一样,在AdaGrad算法中,我们允许每个坐标有单独的学习率。与SGD算法相比,这并没有明显增加AdaGrad的计算代价,因为主要计算用在l(yt,f(xt,w))l(y_t, f(\mathbf{x}_t, \mathbf{w}))l(yt,f(xt,w))及其导数。
注意,在st\mathbf{s}_tst中累加平方梯度意味着st\mathbf{s}_tst基本上以线性速率增长(由于梯度从最初开始衰减,实际上比线性慢一些)。这产生了一个学习率O(t−12)\mathcal{O}(t^{-\frac{1}{2}})O(t−21),但是在单个坐标的层面上进行了调整。对于凸问题,这完全足够了。然而,在深度学习中,我们可能希望更慢地降低学习率。这引出了许多AdaGrad算法的变体。
-
小结:
-
AdaGrad算法会在单个坐标层面动态降低学习率。
-
AdaGrad算法利用梯度的大小作为调整进度速率的手段:用较小的学习率来补偿带有较大梯度的坐标。
-
在深度学习问题中,由于内存和计算限制,计算准确的二阶导数通常是不可行的。梯度可以作为一个有效的代理。
-
如果优化问题的结构相当不均匀,AdaGrad算法可以帮助缓解扭曲。
-
AdaGrad算法对于稀疏特征特别有效,在此情况下由于不常出现的问题,学习率需要更慢地降低。
-
在深度学习问题上,AdaGrad算法有时在降低学习率方面可能过于剧烈。
-
-
-
RMSProp
-
RMSProp算法
Adagrad算法的关键问题之一就是学习率按预定时间表O(t−12)\mathcal{O}(t^{-\frac{1}{2}})O(t−21)显著降低。 而且,Adagrad算法将梯度gt\mathbf{g}_tgt的平方累加成状态矢量st=st−1+gt2\mathbf{s}_t = \mathbf{s}_{t-1} + \mathbf{g}_t^2st=st−1+gt2。因此,由于缺乏规范化,没有约束力,st\mathbf{s}_tst持续增长,几乎上是在算法收敛时呈线性递增。
解决此问题的一种方法是使用st/t\mathbf{s}_t / tst/t。对gt\mathbf{g}_tgt的合理分布来说,它将收敛。遗憾的是,限制行为生效可能需要很长时间,因为该流程记住了值的完整轨迹。
另一种方法是按动量法中的方式使用泄漏平均值,即st←γst−1+(1−γ)gt2\mathbf{s}_t \leftarrow \gamma \mathbf{s}_{t-1} + (1-\gamma) \mathbf{g}_t^2st←γst−1+(1−γ)gt2,其中参数γ>0\gamma > 0γ>0。保持所有其它部分不变就产生了RMSProp算法。公式:
st←γst−1+(1−γ)gt2,xt←xt−1−ηst+ϵ⊙gt.\begin{aligned} \mathbf{s}_t & \leftarrow \gamma \mathbf{s}_{t-1} + (1 - \gamma) \mathbf{g}_t^2, \\ \mathbf{x}_t & \leftarrow \mathbf{x}_{t-1} - \frac{\eta}{\sqrt{\mathbf{s}_t + \epsilon}} \odot \mathbf{g}_t. \end{aligned} stxt←γst−1+(1−γ)gt2,←xt−1−st+ϵη⊙gt.
常数ϵ>0\epsilon > 0ϵ>0通常设置为10−610^{-6}10−6,以确保不会因除以零或步长过大而受到影响。鉴于这种扩展,现在可以自由控制学习率η\etaη,而不考虑基于每个坐标应用的缩放。就泄漏平均值而言,可以采用与之前在动量法中适用的相同推理。扩展st\mathbf{s}_tst定义可获得:
st=(1−γ)gt2+γst−1=(1−γ)(gt2+γgt−12+γ2gt−2+…,).\begin{aligned} \mathbf{s}_t & = (1 - \gamma) \mathbf{g}_t^2 + \gamma \mathbf{s}_{t-1} \\ & = (1 - \gamma) \left(\mathbf{g}_t^2 + \gamma \mathbf{g}_{t-1}^2 + \gamma^2 \mathbf{g}_{t-2} + \ldots, \right). \end{aligned} st=(1−γ)gt2+γst−1=(1−γ)(gt2+γgt−12+γ2gt−2+…,).
同之前一样,使用1+γ+γ2+…,=11−γ1 + \gamma + \gamma^2 + \ldots, = \frac{1}{1-\gamma}1+γ+γ2+…,=1−γ1。因此,权重总和标准化为111且观测值的半衰期为γ−1\gamma^{-1}γ−1。 -
小结
- RMSProp算法与Adagrad算法非常相似,因为两者都使用梯度的平方来缩放系数。
- RMSProp算法与动量法都使用泄漏平均值。但是,RMSProp算法使用该技术来调整按系数顺序的预处理器。
- 在实验中,学习率需要由实验者调度。
- 系数γ\gammaγ决定了在调整每坐标比例时历史记录的时长。
-
-
Adadelta
-
Adadelta算法
Adadelta是AdaGrad的另一种变体,主要区别在于其减少了学习率适应坐标的数量。
此外,广义上Adadelta被称为没有学习率,因为它使用变化量本身作为未来变化的校准。简而言之,Adadelta使用两个状态变量,st\mathbf{s}_tst用于存储梯度二阶导数的泄露平均值,Δxt\Delta\mathbf{x}_tΔxt用于存储模型本身中参数变化二阶导数的泄露平均值。
以下是Adadelta的技术细节。
首先获得泄露更新:
st=ρst−1+(1−ρ)gt2.\begin{aligned} \mathbf{s}_t & = \rho \mathbf{s}_{t-1} + (1 - \rho) \mathbf{g}_t^2. \end{aligned} st=ρst−1+(1−ρ)gt2.
与 RMSProp的区别在于,本算法使用重新缩放的梯度gt′\mathbf{g}_t'gt′执行更新,即
xt=xt−1−gt′.\begin{aligned} \mathbf{x}_t & = \mathbf{x}_{t-1} - \mathbf{g}_t'. \\ \end{aligned} xt=xt−1−gt′.
对于调整后的梯度gt′\mathbf{g}_t'gt′:
gt′=Δxt−1+ϵst+ϵ⊙gt,\begin{aligned} \mathbf{g}_t' & = \frac{\sqrt{\Delta\mathbf{x}_{t-1} + \epsilon}}{\sqrt{{\mathbf{s}_t + \epsilon}}} \odot \mathbf{g}_t, \\ \end{aligned} gt′=st+ϵΔxt−1+ϵ⊙gt,
其中Δxt−1\Delta \mathbf{x}_{t-1}Δxt−1是重新缩放梯度的平方gt′\mathbf{g}_t'gt′的泄漏平均值。首先将Δx0\Delta \mathbf{x}_{0}Δx0初始化为000,然后在每个步骤中使用gt′\mathbf{g}_t'gt′更新它,即
Δxt=ρΔxt−1+(1−ρ)gt′2,\begin{aligned} \Delta \mathbf{x}_t & = \rho \Delta\mathbf{x}_{t-1} + (1 - \rho) {\mathbf{g}_t'}^2, \end{aligned} Δxt=ρΔxt−1+(1−ρ)gt′2,
ϵ\epsilonϵ(例如10−510^{-5}10−5这样的小值)是为了保持数字稳定性而加入的。 -
小结
-
Adadelta没有学习率参数。相反,它使用参数本身的变化率来调整学习率。
-
Adadelta需要两个状态变量来存储梯度的二阶导数和参数的变化。
-
Adadelta使用泄漏的平均值来保持对适当统计数据的运行估计。
-
-
-
Adam算法
-
Adam算法:
Adam算法的关键组成部分之一是:使用指数加权移动平均值来估算梯度的动量和二次矩,即它使用状态变量:
vt←β1vt−1+(1−β1)gt,st←β2st−1+(1−β2)gt2.\begin{aligned} \mathbf{v}_t & \leftarrow \beta_1 \mathbf{v}_{t-1} + (1 - \beta_1) \mathbf{g}_t, \\ \mathbf{s}_t & \leftarrow \beta_2 \mathbf{s}_{t-1} + (1 - \beta_2) \mathbf{g}_t^2. \end{aligned} vtst←β1vt−1+(1−β1)gt,←β2st−1+(1−β2)gt2.
这里β1\beta_1β1和β2\beta_2β2是非负加权参数。常将它们设置为β1=0.9\beta_1 = 0.9β1=0.9和β2=0.999\beta_2 = 0.999β2=0.999。也就是说,方差估计的移动远远慢于动量估计的移动。注意,如果我们初始化v0=s0=0\mathbf{v}_0 = \mathbf{s}_0 = 0v0=s0=0,就会获得一个相当大的初始偏差。可以通过使用∑i=0tβi=1−βt1−β\sum_{i=0}^t \beta^i = \frac{1 - \beta^t}{1 - \beta}∑i=0tβi=1−β1−βt来解决这个问题。相应地,标准化状态变量由下式获得
v^t=vt1−β1tand s^t=st1−β2t.\hat{\mathbf{v}}_t = \frac{\mathbf{v}_t}{1 - \beta_1^t} \text{ and } \hat{\mathbf{s}}_t = \frac{\mathbf{s}_t}{1 - \beta_2^t}. v^t=1−β1tvt and s^t=1−β2tst.
有了正确的估计,我们现在可以写出更新方程。首先,我们以非常类似于RMSProp算法的方式重新缩放梯度以获得
gt′=ηv^ts^t+ϵ.\mathbf{g}_t' = \frac{\eta \hat{\mathbf{v}}_t}{\sqrt{\hat{\mathbf{s}}_t} + \epsilon}. gt′=s^t+ϵηv^t.
与RMSProp不同,我们的更新使用动量v^t\hat{\mathbf{v}}_tv^t而不是梯度本身。此外,由于使用1s^t+ϵ\frac{1}{\sqrt{\hat{\mathbf{s}}_t} + \epsilon}s^t+ϵ1而不是1s^t+ϵ\frac{1}{\sqrt{\hat{\mathbf{s}}_t + \epsilon}}s^t+ϵ1进行缩放,两者会略有差异。前者在实践中效果略好一些,因此与RMSProp算法有所区分。通常,选择ϵ=10−6\epsilon = 10^{-6}ϵ=10−6,这是为了在数值稳定性和逼真度之间取得良好的平衡。最后,简单更新:
xt←xt−1−gt′.\mathbf{x}_t \leftarrow \mathbf{x}_{t-1} - \mathbf{g}_t'. xt←xt−1−gt′.
回顾Adam算法,其设计灵感很清楚:首先,动量和规模在状态变量中清晰可见,其相当独特的定义使我们移除偏项(这可以通过稍微不同的初始化和更新条件来修正)。其次,RMSProp算法中两项的组合都非常简单。最后,明确的学习率η\etaη使我们能够控制步长来解决收敛问题。
-
Yogi
Adam算法也存在一些问题:即使在凸环境下,当st\mathbf{s}_tst的二次矩估计值爆炸时,它可能无法收敛。为此,有人为st\mathbf{s}_tst提出了改进的更新和参数初始化。论文中建议重写Adam算法更新如下:
st←st−1+(1−β2)(gt2−st−1).\mathbf{s}_t \leftarrow \mathbf{s}_{t-1} + (1 - \beta_2) \left(\mathbf{g}_t^2 - \mathbf{s}_{t-1}\right). st←st−1+(1−β2)(gt2−st−1).
每当gt2\mathbf{g}_t^2gt2具有值很大的变量或更新很稀疏时,st\mathbf{s}_tst可能会太快地“忘记”过去的值。一个有效的解决方法是将gt2−st−1\mathbf{g}_t^2 - \mathbf{s}_{t-1}gt2−st−1替换为gt2⊙sgn(gt2−st−1)\mathbf{g}_t^2 \odot \mathop{\mathrm{sgn}}(\mathbf{g}_t^2 - \mathbf{s}_{t-1})gt2⊙sgn(gt2−st−1)。这就是Yogi更新,现在更新的规模不再取决于偏差的量。
st←st−1+(1−β2)gt2⊙sgn(gt2−st−1).\mathbf{s}_t \leftarrow \mathbf{s}_{t-1} + (1 - \beta_2) \mathbf{g}_t^2 \odot \mathop{\mathrm{sgn}}(\mathbf{g}_t^2 - \mathbf{s}_{t-1}). st←st−1+(1−β2)gt2⊙sgn(gt2−st−1).
论文中,作者还进一步建议用更大的初始批量来初始化动量,而不仅仅是初始的逐点估计。 -
小结
-
Adam算法将许多优化算法的功能结合到了相当强大的更新规则中。
-
Adam算法在RMSProp算法基础上创建的,还在小批量的随机梯度上使用EWMA。
-
在估计动量和二次矩时,Adam算法使用偏差校正来调整缓慢的启动速度。
-
对于具有显著差异的梯度,我们可能会遇到收敛性问题。我们可以通过使用更大的小批量或者切换到改进的估计值st\mathbf{s}_tst来修正它们。Yogi提供了这样的替代方案。
-
-
-
算法小结
- Gradient Descent: 提供了优化模型的一种理论方法。
- SGD: 随机梯度下降在解决优化问题时比梯度下降更有有效。
- Minibatch-SGD:在一个小批量中使用更大的观测数据集,可以通过向量化提供额外的效率。这是高效的多机、多GPU和并行处理的关键。
- Momentum: 添加一种机制,用于汇聚过去历史梯度来加速收敛。
- Adagrad: 用过对每个坐标缩放实现高效的计算预处理器。
- RMSProp: Adagrad算法的一个变体,通过学习率的调整来分离每个坐标的缩放。
- Adadelta: Adagrad算法的一个变体,其减少了学习率适应坐标的数量。广义上Adadelta被称为没有学习率。
- Adam: 是2、3、4、5和6的集大成者。
-
相关文章:

深度学习优化算法总结
深度学习的优化算法 优化的目标 优化提供了一种最大程度减少深度学习损失函数的方法,但本质上,优化和深度学习的目标不同。 优化关注的是最小化目标;深度学习是在给定有限数据量的情况下寻找合适的模型。 优化算法 gradient descent…...

CMake详细使用
1、CMake简介CMake是一个用于管理源代码的跨平台构建工具可以方便地根据目标平台和编译工具产生对应的编译文件主要用于C/C语言的构建,但是也可以用于其它编程语言的源代码。如同使用make命令工具解析Makefile文件一样cmake命令工具依赖于一个CMakeLists.txt的文件该…...
【数据结构与算法】前缀树的实现
🌠作者:阿亮joy. 🎆专栏:《数据结构与算法要啸着学》 🎇座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根 目录👉…...
canvas 制作2048
效果展示 对UI不满意可以自行调整,这里只是说一下游戏的逻辑,具体的API调用不做过多展示。 玩法分析 2048 的玩法非常简单,通过键盘的按下,所有的数字都向着同一个方向移动,如果出现两个相同的数字,就将…...

playwright: 全局修改页面等待超时时间
等待超时时间默认是30s, 可以通过以下几个方法设置: browser_context.set_default_navigation_timeout()browser_context.set_default_timeout()page.set_default_navigation_timeout()page.set_default_timeout() set_default_navigation_timeout set_default_n…...

C++类和对象(中)
✨个人主页: Yohifo 🎉所属专栏: C修行之路 🎊每篇一句: 图片来源 I do not believe in taking the right decision. I take a decision and make it right. 我不相信什么正确的决定。我都是先做决定,然后把…...

Docker安装EalasticSearch、Kibana,安装Elasticvue插件
使用Docker快速安装部署ES和Kibana的前提:首先需要确保已经安装了Docker环境。 如果没有安装Docker的话,先在Linux上安装Docker。 有了Docker环境后,就可以使用Docker安装部署ES和Kibana了 一、安装ES 1、拉取EalasticSearch镜像 docker p…...

算法训练营 day39 贪心算法 无重叠区间 划分字母区间 合并区间
算法训练营 day39 贪心算法 无重叠区间 划分字母区间 合并区间 无重叠区间 435. 无重叠区间 - 力扣(LeetCode) 给定一个区间的集合 intervals ,其中 intervals[i] [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互…...
c/c++开发,无可避免的文件访问开发案例
一、缓存文件系统 ANSI C标准中的C语言库提供了fopen, fclose, fread, fwrite, fgetc, fgets, fputc, fputs, freopen, fseek, ftell, rewind等标准函数,这些函数在不同的操作系统中应该调用不同的内核API,从而支持开发者跨平台实现对文件的访问。 在Lin…...

MySQL学习笔记
MySQL学习笔记一、基础配置二、数据库操作三、表的操作1.创建表2.表选项3.查看表4.修改表5.删除表6.复制表7.检查优化修复表四、数据操作基础增删改查五、字符集编码六、数据类型(列类型)1.数值类型2.字符串类型3.日期时间类型4.枚举和集合七、列属性&am…...
ccs导入工程失败的处理方法
文章目录当导入CCS新工程时出现下述错误怎么办?方法一 从TI官网下载安装包进行安装,下载链接:软件下载完成 安装路径为上面的文件夹点击安装完成后,导入安装路径,并点击Refresh按钮,依据路径进行更新&#…...

探针台常见的故障及解决方法
症状、 可能原因、 解决方法 移动样品后画面变模糊 —显微镜不垂直,调垂直显微镜 样品台不水平 —调水平样品台 显微镜视场亮度不足,边缘切割或看不到像—转换器不在定位位置上 把转换器转到定位位置上 管镜转盘不在定位位置上 —把管镜转盘转到定…...

域内资源探测
✅作者简介:CSDN内容合伙人、信息安全专业在校大学生🏆 🔥系列专栏 :内网安全 📃新人博主 :欢迎点赞收藏关注,会回访! 💬舞台再大,你不上台,永远是…...
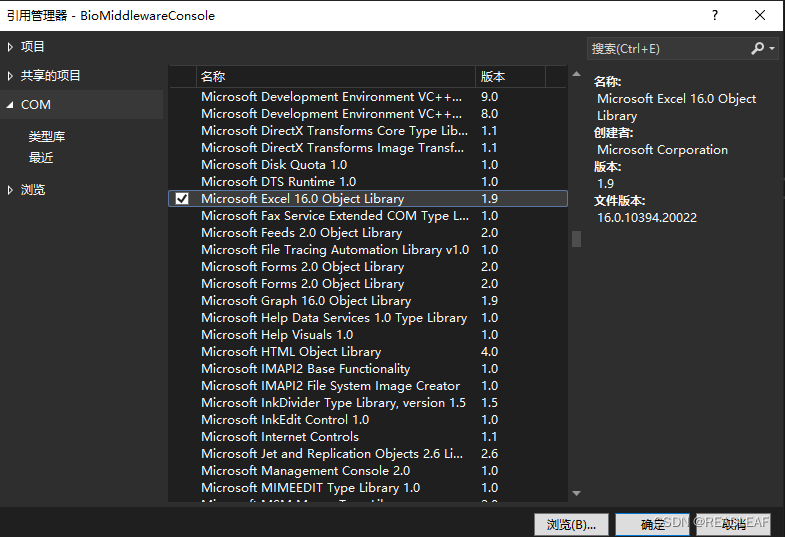
c# 将数据导出到EXCEL文件
第一步:项目中加入引用。 在鼠标右击项目,点击【添加】弹出菜单列表,选择【项目引用】弹出【引用管理器】对话框,选择【COM】-【Microsoft Excel 16.0 Object Library】,如图所示: 第二步,编辑…...
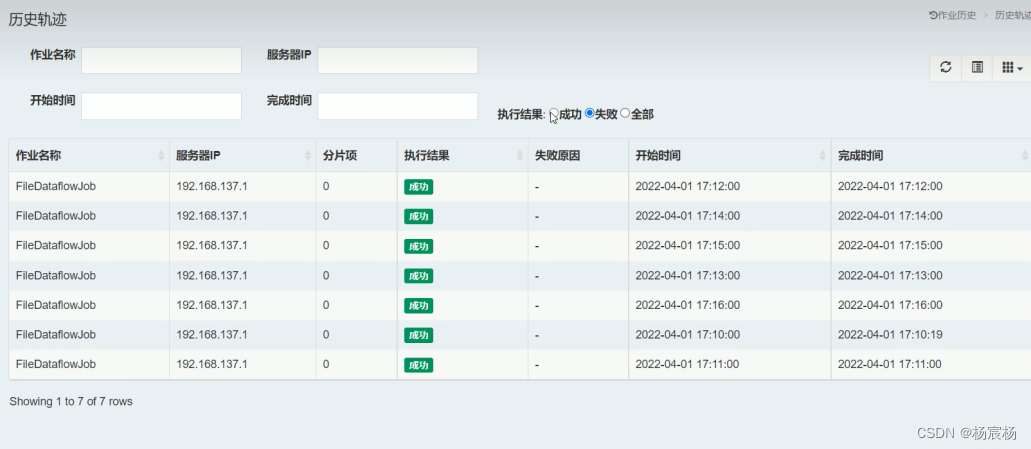
微服务 分片 运维管理
微服务 分片 运维管理分片分片的概念分片案例环境搭建案例改造成任务分片Dataflow类型调度代码示例运维管理事件追踪运维平台搭建步骤使用步骤分片 分片的概念 当只有一台机器的情况下,给定时任务分片四个,在机器A启动四个线程,分别处理四个…...

批量占满TEMP表空间问题处理与排查
批量占满TEMP表空间问题处理与排查应急处置问题排查查看占用TEMP表空间高的SQL获取目标SQL执行计划方法一:EXPLAIN PLAN FOR方法二:DBMS_XPLAN.DISPLAY_CURSOR方法三:DBMS_XPLAN.DISPLAY_AWR方法四:AUTOTRACE数据库跑批任务占满TE…...

Pytorch中的tensor和variable
Tensor与Variable pytorch两个基本对象:Tensor(张量)和Variable(变量) 其中,tensor不能反向传播,variable可以反向传播(forword)。 反向传播是为了让神经网络更新前面…...
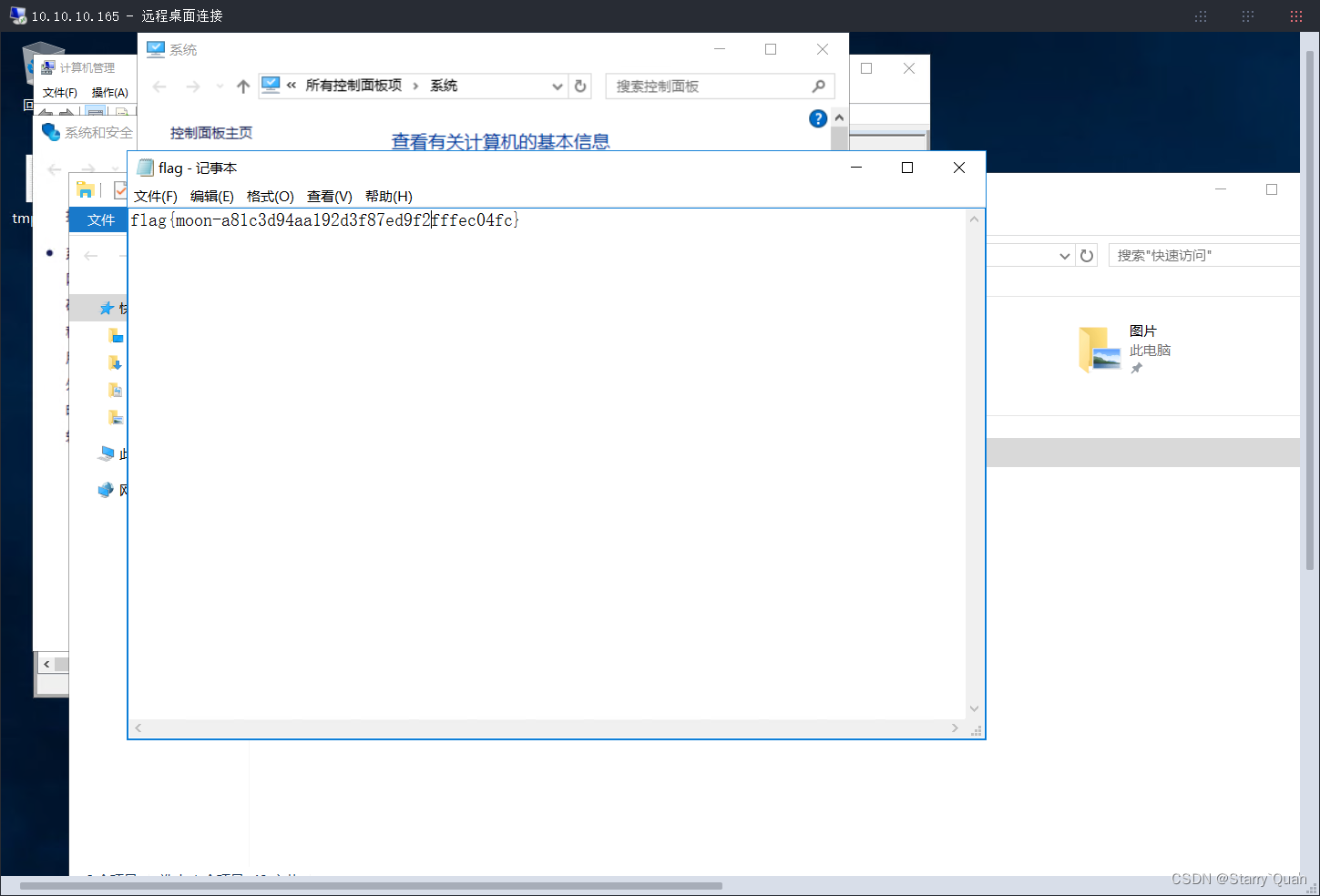
暗月内网渗透实战——项目七
首先环境配置 VMware的网络配置图 环境拓扑图 开始渗透 信息收集 使用kali扫描一下靶机的IP地址 靶机IP:192.168.0.114 攻击机IP:192.168.0.109 获取到了ip地址之后,我们扫描一下靶机开放的端口 靶机开放了21,80,999,3389,5985,6588端口…...

【Java 面试合集】描述下Objec类中常用的方法(未完待续中...)
描述下Objec类中常用的方法 1. 概述 首先我们要知道Object 类是所有的对象的基类,也就是所有的方法都是可以被重写的。 那么到底哪些方法是我们常用的方法呢??? cloneequalsfinalizegetClasshashCodenotifynotifyAlltoStringw…...

SQLSERVER 的 truncate 和 delete 有区别吗?
一:背景 1. 讲故事 在面试中我相信有很多朋友会被问到 truncate 和 delete 有什么区别 ,这是一个很有意思的话题,本篇我就试着来回答一下,如果下次大家遇到这类问题,我的答案应该可以帮你成功度过吧。 二࿱…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
