当前位置： 首页 > news >正文

线性代数（四）| 解方程 齐次性 非齐次性 扩充问题

news 2026/2/10 1:05:37

文章目录

  • 1 方程解的个数
  • 2 解方程步骤
    • 2.1 齐次性方程组
    • 2.2 非齐次方程组
  • 3 一些扩充问题

系数矩阵 增广矩阵

A m × n X = B A_{m×n}X=B Am×n​X=B

1 方程解的个数

m 代表有m个方程 n代表有n个未知数

系数矩阵的秩与增广矩阵的秩不同 无解

若相同 ，如系数矩阵的秩和未知数个数n相同，则有唯一解，若系数矩阵的秩小于未知数个数n，则有无穷多解

在这里插入图片描述

2 解方程步骤

2.1 齐次性方程组

（1） 写出系数矩阵

（2）初等变换到行简化阶梯矩阵

（3）写出同解方程组

（4）赋值写出基础解系

例题：求解方程组

在这里插入图片描述

在这里插入图片描述

2.2 非齐次方程组

齐次性方程组的通解加上非齐次性方程组的一个特解

（1） 写出增广矩阵

（2）初等行变换到行简化阶梯矩阵

（3）写出同解方程组代入特值求出一个特解

（4）去掉常量代入特值求得齐次性方程组的通解

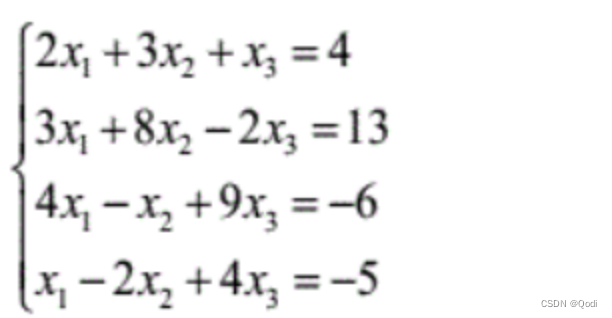
在这里插入图片描述

在这里插入图片描述

3 一些扩充问题

1、线性无关线性相关相结合的知识点

在这里插入图片描述

求齐次性方程组的通解加上一个非齐次性方程组的一个特解

相关文章：

线性代数（四）| 解方程 齐次性 非齐次性 扩充问题

文章目录 1 方程解的个数2 解方程步骤2.1 齐次性方程组2.2 非齐次方程组 3 一些扩充问题 系数矩阵 增广矩阵 A m n X B A_{mn}XB Amn​XB 1 方程解的个数 m 代表有m个方程 n代表有n个未知数 系数矩阵的秩与增广矩阵的秩不同 无解 若相同 ，如系数矩阵的秩和未知…...

编程日记 2023/11/15 3:39:39

快乐数问题

编写一个算法来判断一个数 n 是不是快乐数。 「快乐数」 定义为： 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。 如果这个过程 结果为 1&#xff…...

编程日记 2023/11/15 3:38:38

8 历史服务器配置

为了查看程序的历史运行情况&#xff0c;需要配置一下历史服务器 1、配置mapred-site.xml vim mapred-site.xml在该文件里面增加如下配置 //原先的配置不用删除 <!-- 历史服务器端地址 --> <property><name>mapreduce.jobhistory.address</name><…...

编程日记 2023/11/15 3:37:37

读书笔记：《精益数据分析》

《精益数据分析 . Lean Analytics Use Data to Build a Better Startup Faster》 加 . 阿利斯泰尔 . 克罗尔 本杰明 . 尤科维奇 著&#xff0c;韩知白 王鹤达 译 2023.7.27 ~ 2023.11.4 本以为是本纯数学的、介绍公式的数据分析用法的书&#xff0c;结果是&#xff1a;…...

编程日记 2023/11/15 3:36:36

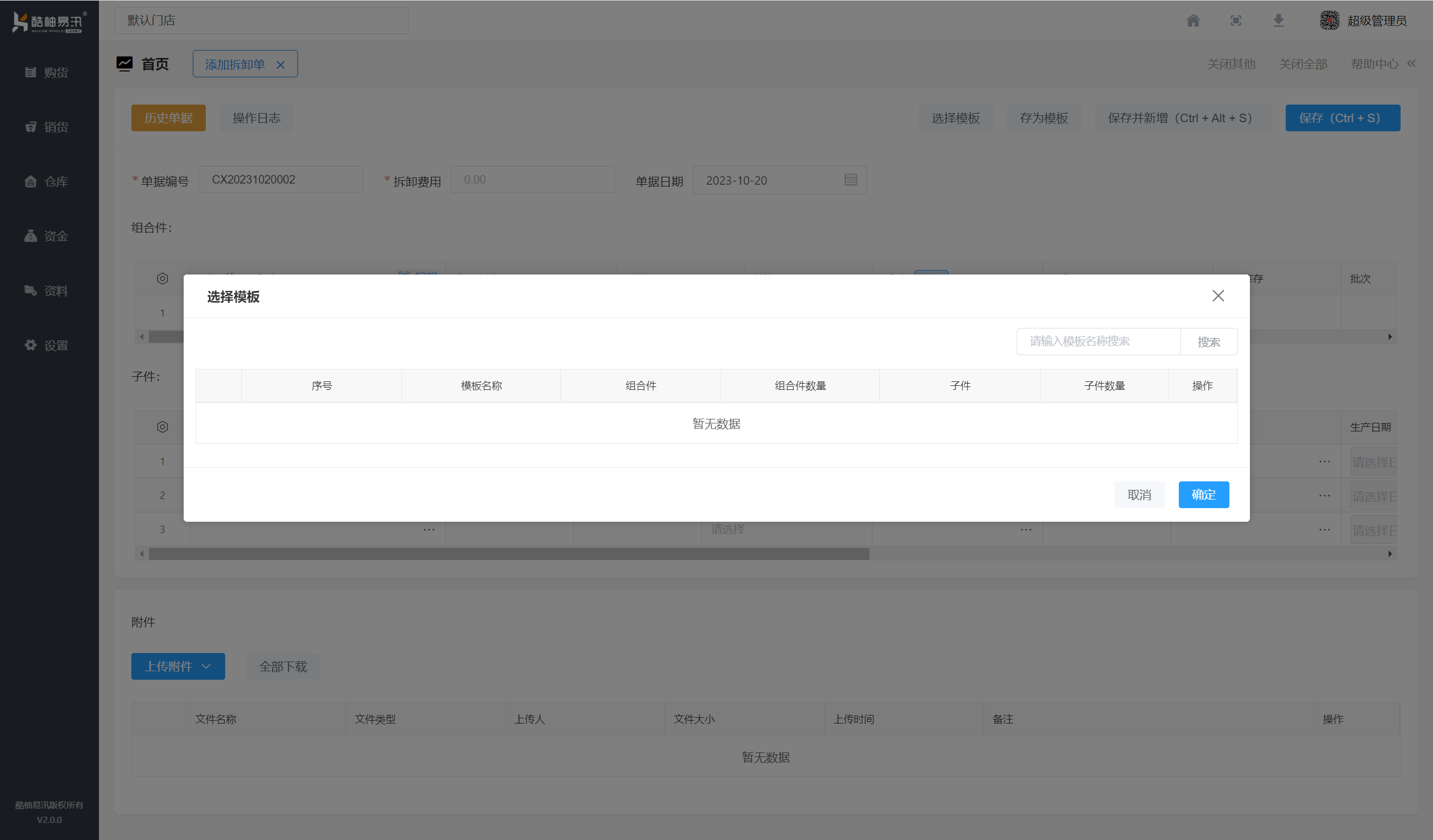
酷柚易汛ERP- 组装单与拆卸单操作

1、功能介绍 组装单用来处理企业组装等加工业务&#xff0c;拆卸单用来处理企业拆卸等加工业务&#xff0c;支持一对多的产品加工业务。 2、主要操作 2.1 新增组装单 打开【仓库】-【组装单】新增组装单。 录入组合件与子件&#xff0c;单据审核后&#xff0c;系统根据存货…...

编程日记 2023/11/15 3:35:34

yolov8训练

介绍 训练深度学习模型包括向其提供数据并调整其参数&#xff0c;以便其能够做出准确的预测。Ultralytics YOLOv8中的训练模式旨在充分利用现代硬件功能&#xff0c;对目标检测模型进行有效和高效的训练。本指南旨在涵盖使用YOLOv8强大的一组功能开始训练自己的模型所需的所有细…...

编程日记 2023/11/15 3:34:33

抖音短视频账号矩阵系统、短视频矩阵源码+无人直播源码开发可打包

抖音短视频账号矩阵系统、短视频矩阵源码无人直播源码开发可打包 矩阵系统源码主要有三种框架&#xff1a;Spring、Struts和Hibernate。Spring框架是一个全栈式的Java应用程序开发框架&#xff0c;提供了IOC容器、AOP、事务管理等功能。Struts框架是一个MVC架构的Web应用程序框…...

编程日记 2023/11/15 3:33:32

NI和EttusResearchUSRP设备之间的区别

NI和EttusResearchUSRP设备之间的区别 概述 USRP&#xff08;通用软件无线电外设&#xff09;设备是业界领先的商软件定义无线电&#xff08;SDR&#xff09;。全球数以千计的工程师使用USRPSDR来快速设计、原型设计和部署无线系统。它们以两个不同的品牌进行营销和销售&…...

编程日记 2023/11/15 3:32:31

WPF UI样式介绍

WPF&#xff08;Windows Presentation Foundation&#xff09;是微软的一个用于创建桌面客户端应用程序的UI框架。WPF使用XAML&#xff08;可扩展应用程序标记语言&#xff09;作为其界面设计语言&#xff0c;这使得开发者能够以声明性方式定义UI元素和布局。 在WPF中&#xf…...

编程日记 2023/11/15 3:31:30

【开源】基于Vue.js的校园失物招领管理系统的设计和实现

目录 一、摘要1.1 项目介绍1.2 项目详细录屏 二、研究内容2.1 招领管理模块2.2 寻物管理模块2.3 系统公告模块2.4 感谢留言模块 三、界面展示3.1 登录注册3.2 招领模块3.3 寻物模块3.4 公告模块3.5 感谢留言模块3.6 系统基础模块 四、免责说明 一、摘要 1.1 项目介绍 基于Vue…...

编程日记 2023/11/15 3:29:29

计算机视觉中目标检测的数据预处理

本文涵盖了在解决计算机视觉中的目标检测问题时&#xff0c;对图像数据执行的预处理步骤。 首先&#xff0c;让我们从计算机视觉中为目标检测选择正确的数据开始。在选择计算机视觉中的目标检测最佳图像时&#xff0c;您需要选择那些在训练强大且准确的模型方面提供最大价值的图…...

编程日记 2023/11/15 3:28:27

es 查询多个索引的文档

es 查询多个索引 第一种做法&#xff1a; 多个索引&#xff0c;用逗号隔开 GET /book_2020_09,book_2021_09/_search第二种做法&#xff1a; 可以用 * 模糊匹配。。比如 book* &#xff0c;表示查询所有 book开头的 索引。 GET /book*/_search GET /*book*/_search第二种做…...

编程日记 2023/11/15 3:25:23

用java把服务器某个目录日志实时打印出来

1.引入第三方包 <dependency><groupId>com.jcraft</groupId><artifactId>jsch</artifactId><version>0.1.55</version> </dependency>2.代码如下 import com.jcraft.jsch.ChannelExec; import com.jcraft.jsch.JSch; import …...

编程日记 2023/11/15 3:22:20

金融信贷行业如何准确——大数据精准定位获客渠道

通过大数据精准获客&#xff0c;不仅可以及时拦截网址浏览量&#xff0c;还可以访问移动贷款应用软件的高频活跃客户和新注册客户。此外&#xff0c;通过大数据进行准确的客户获取&#xff0c;还可以获得电话座机号码的实时通信记录&#xff0c;捕捉小程序应用程序和关键词搜索…...

编程日记 2023/11/15 3:21:19

LeetCode 面试题 16.21. 交换和

文章目录 一、题目二、C# 题解 一、题目 给定两个整数数组&#xff0c;请交换一对数值&#xff08;每个数组中取一个数值&#xff09;&#xff0c;使得两个数组所有元素的和相等。 返回一个数组&#xff0c;第一个元素是第一个数组中要交换的元素&#xff0c;第二个元素是第二…...

编程日记 2023/11/15 3:20:18

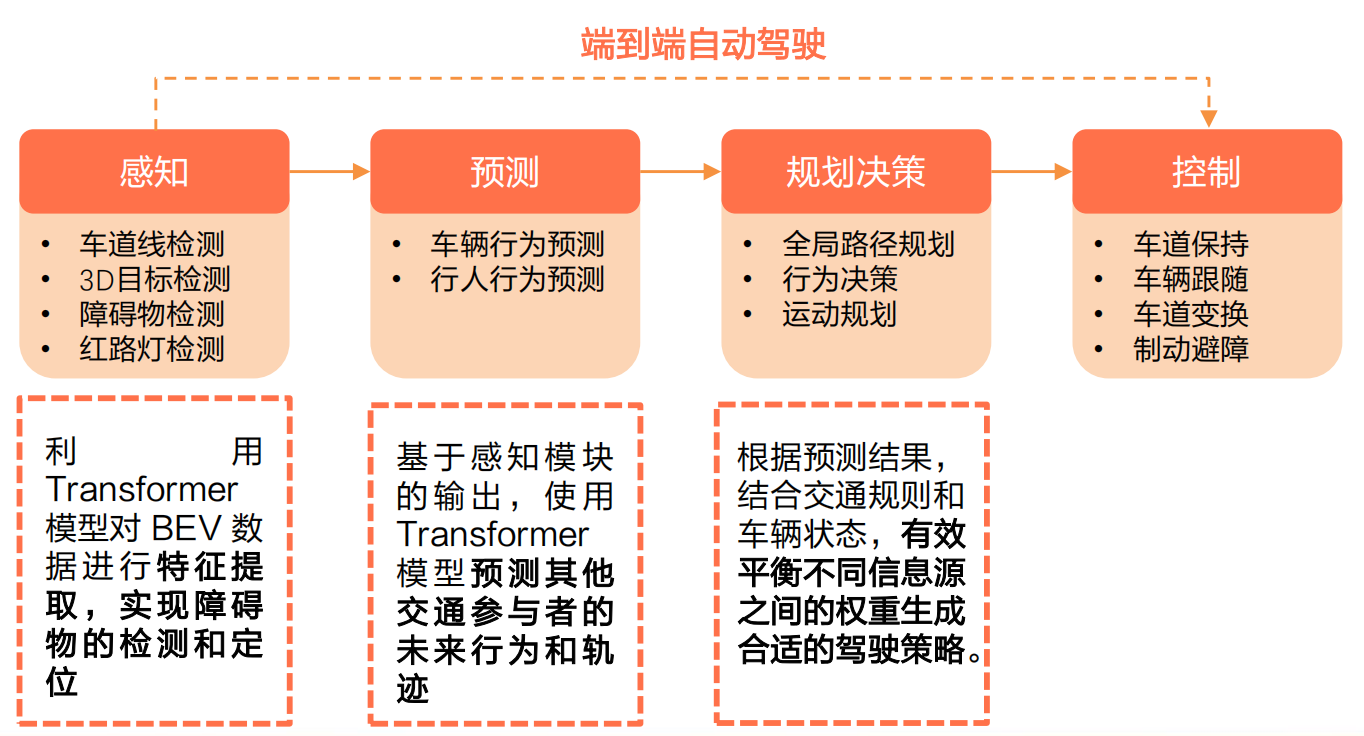
未来之路：大模型技术在自动驾驶的应用与影响

本文深入分析了大模型技术在自动驾驶领域的应用和影响&#xff0c;万字长文&#xff0c;慢慢观看~ 文中首先概述了大模型技术的发展历程&#xff0c;自动驾驶模型的迭代路径&#xff0c;以及大模型在自动驾驶行业中的作用。接着&#xff0c;详细介绍了大模型的基本定义、基础功…...

编程日记 2023/11/15 3:19:17

Skywalking流程分析_5(字节码增强)

SkyWalkingAgent.Transformer#transform 此方法就是进行字节码增强的过程 private static class Transformer implements AgentBuilder.Transformer {private PluginFinder pluginFinder;Transformer(PluginFinder pluginFinder) {this.pluginFinder pluginFinder;}Override…...

编程日记 2023/11/15 3:18:16

Windows conan环境搭建

Windows conan环境搭建 1 安装conan1.1 安装依赖软件1.1.1 python安装1.1.2 git bash安装1.1.3 安装Visual Studio Community 20191.1.3.1 选择安装的组件1.1.3.2 选择要支持的工具以及对应的SDK 1.1.4 vscode安装 1.3 验证conan功能1.4 查看conancenter是否包含poco包1.5 查看…...

编程日记 2023/11/15 3:17:14

如何使用Cpolar+Tipask，在ubuntu系统上搭建一个私人问答网站

文章目录 前言2.Tipask网站搭建2.1 Tipask网站下载和安装2.2 Tipask网页测试2.3 cpolar的安装和注册 3. 本地网页发布3.1 Cpolar临时数据隧道3.2 Cpolar稳定隧道&#xff08;云端设置&#xff09;3.3 Cpolar稳定隧道&#xff08;本地设置&#xff09; 4. 公网访问测试5. 结语 前…...

编程日记 2023/11/15 3:16:13

怎么在uni-app中使用Vuex(第一篇)

Vuex简介 vuex的官方网址如下 https://vuex.vuejs.org/zh/ 阅读官网请带着几个问题去阅读&#xff1a; vuex用于什么场景&#xff1f;vuex能给我们带来什么好处&#xff1f;我们为什么要用vuex?vuex如何实现状态集中管理&#xff1f; Vuex用于哪些场景&#xff1f; 组件之…...

编程日记 2023/11/15 3:15:12

web vue 项目 Docker化部署

Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段&#xff1a; 构建阶段&#xff08;Build Stage&#xff09;&#xff1a…...

编程新知 2025/8/12 16:28:43

【JVM】- 内存结构

引言 JVM&#xff1a;Java Virtual Machine 定义&#xff1a;Java虚拟机&#xff0c;Java二进制字节码的运行环境好处&#xff1a; 一次编写&#xff0c;到处运行自动内存管理&#xff0c;垃圾回收的功能数组下标越界检查&#xff08;会抛异常&#xff0c;不会覆盖到其他代码…...

编程新知 2026/1/30 13:40:43

抖音增长新引擎：品融电商，一站式全案代运营领跑者

抖音增长新引擎&#xff1a;品融电商&#xff0c;一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中&#xff0c;品牌如何破浪前行&#xff1f;自建团队成本高、效果难控&#xff1b;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

编程新知 2026/2/1 5:45:17

2.Vue编写一个app

1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

编程新知 2026/1/31 6:04:01

微信小程序云开发平台MySQL的连接方式

注&#xff1a;微信小程序云开发平台指的是腾讯云开发 先给结论&#xff1a;微信小程序云开发平台的MySQL&#xff0c;无法通过获取数据库连接信息的方式进行连接&#xff0c;连接只能通过云开发的SDK连接&#xff0c;具体要参考官方文档&#xff1a; 为什么&#xff1f; 因为…...

编程新知 2026/2/1 5:24:17

第 86 场周赛：矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词

Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵&#xff0c;其中每行&#xff0c;每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid&#xff0c;其中有多少个 3 3 的 “幻方” 子矩阵&am…...

编程新知 2026/2/7 13:27:36

10-Oracle 23 ai Vector Search 概述和参数

一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI&#xff0c;使用客户端或是内部自己搭建集成大模型的终端&#xff0c;加速与大型语言模型&#xff08;LLM&#xff09;的结合&#xff0c;同时使用检索增强生成&#xff08;Retrieval Augmented Generation &#…...

编程新知 2026/2/9 20:30:28

LLMs 系列实操科普（1）

写在前面&#xff1a; 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容&#xff0c;原视频时长 ~130 分钟&#xff0c;以实操演示主流的一些 LLMs 的使用&#xff0c;由于涉及到实操&#xff0c;实际上并不适合以文字整理&#xff0c;但还是决定尽量整理一份笔…...

编程新知 2026/1/31 11:35:24

作为测试我们应该关注redis哪些方面

1、功能测试 数据结构操作&#xff1a;验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化&#xff1a;测试aof和aof持久化机制&#xff0c;确保数据在开启后正确恢复。 事务&#xff1a;检查事务的原子性和回滚机制。 发布订阅&#xff1a;确保消息正确传递。 2、性…...

编程新知 2025/11/1 2:00:51

通过MicroSip配置自己的freeswitch服务器进行调试记录

之前用docker安装的freeswitch的&#xff0c;启动是正常的&#xff0c; 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

编程新知 2026/2/6 14:23:05