【Python】上市公司数据进行经典OLS回归实操
- 一、题目
- 二、数据合并、清洗、描述性统计
- 1、数据获取
- 2、数据合并
- 3、选择董监高薪酬作为解释变量的理论逻辑分析
- 三、多元回归模型的参数估计、结果展示与分析
- 1、描述性统计分析
- 2、剔除金融类上市公司
- 3、对所有变量进行1%缩尾处理
- 4、0-1标准化,所有解释变量
- 5、绘制热力图
- 6、逐步加入关键解释变量
- 7、制作显著性表格
- 8、经典logit回归
- 首先,一件非常崩溃的事情,昨天晚上使用jupyter notebook跑的数据、代码全部没了,非常难受。
- 不过好在自己
足够坚强,反思了一下,当时要关闭的时候显示未保存,但是明明自己保存了,所以还是自己的问题。其次,我懂得了以后使用jupyter notebook 会更加小心谨慎。 - 过一段重装一下,看看是什么原因导致无法正常保存。
一、题目

- 四个文件的资料已经放在Q群里面了
二、数据合并、清洗、描述性统计
1、数据获取
- 从CSMAR【国泰安金融数据库】数据库下载上市公司基本信息、个股日度收益率、公司董监高等高管个人资料(含个人特征、兼任信息、总经理变更等)、关联交易or股权质押or交叉持股情况、财务指标(包括比率结构、相对价值指标、盈利能力指标)
- 当然,我实际用到的数据没有那么多,就4个表格。
df1数据如下:
df2数据如下:
df3数据如下:

df4数据如下:
- df4的数据我只使用了报告期薪酬这列数据,与上面的三张表格的部分数据进行合并。
- 此外发现统计截止日期都是同一个日期,因此需要进行处理。
2、数据合并
from scipy.stats.mstats import winsorize
import statsmodels.api as sma
from sklearn.preprocessing import MinMaxScaler # min-max 标准化
import pandas as pd
import numpy as np
df1=pd.read_excel("比例结构.xlsx")
df2=pd.read_excel("相对价值指标.xlsx")
df3=pd.read_excel("盈利能力.xlsx")
df4=pd.read_excel("副本董监高个人特征文件.xlsx")
# 删除'报告期报酬总额'列为空的行
df4 = df4[df4['报告期报酬总额']>0]
import pandas as pd# 假设df1, df2, df3已经被创建并且包含了相应的列# 首先,合并df1和df2
data1 = pd.merge(df1[['Stkcd', '股票简称', '统计截止日期', '流动资产比率', '现金资产比率', '固定资产比率', '无形资产比率', '有形资产比率', '资产负债率','归属于母公司净利润占比', '主营业务利润占比']], df2[['Stkcd', '股票简称', '统计截止日期', '市盈率(PE)1', '市净率母公司(PB)', '托宾Q值B', '账面市值比A']], on=['Stkcd', '股票简称', '统计截止日期'], how='inner')# 然后,将df4与df3合并
data1 = pd.merge(data1, df3[['Stkcd', '股票简称', '统计截止日期', '销售费用率', '管理费用率', '总资产净利润率(ROA)A']], on=['Stkcd', '股票简称', '统计截止日期'], how='inner')# 现在df4包含了所有需要的列
# 缺失值直接去除
data1=data1.dropna()
data1
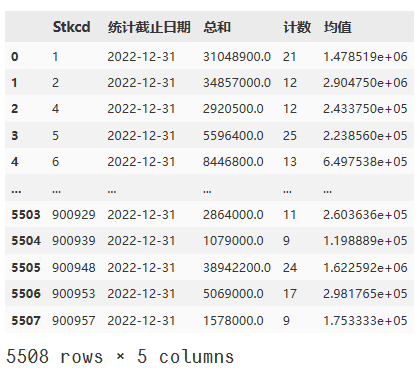
# 对df4的数据进行处理,使用groupby和agg进行聚合操作
df44 = df4.groupby(['Stkcd', '统计截止日期']).agg({'报告期报酬总额': ['sum', 'count']})# 重命名列名
df44.columns = ['总和', '计数']# 计算均值
df44['均值'] = df44['总和'] / df44['计数']# 重置索引以获得所需的结果
df44.reset_index(inplace=True)
df44 = pd.DataFrame(df44)
df44
# 然后,将df4与df3合并
data1 = pd.merge(data1, df44[['Stkcd', '均值']], on=['Stkcd'], how='inner')
data1
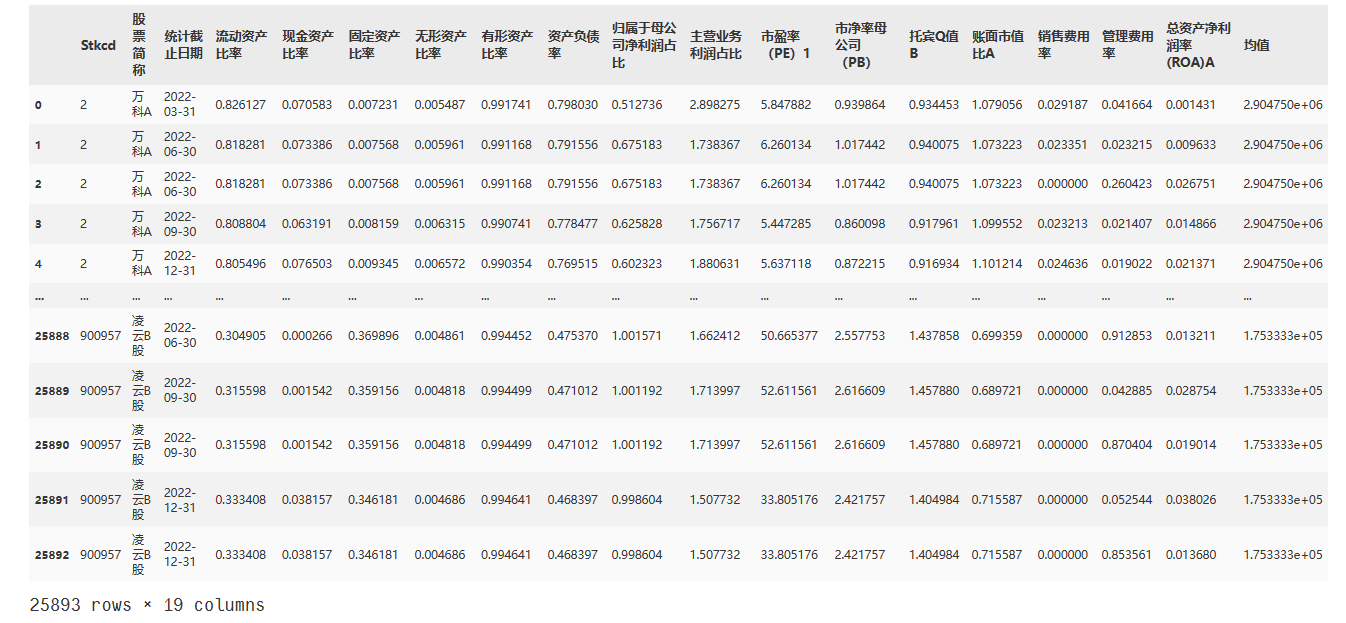
data1.rename(columns={'均值': '董监高报告期报酬均值'}, inplace=True)
data1.columns
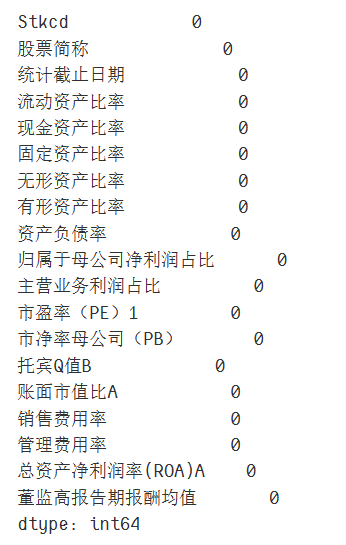
data1.isnull().sum()
被解释变量:
- 总资产净利润率(ROA)A :指的是企业总资产的净利润率,是一种衡量公司经营效率的财务指标。
解释变量:
-
流动资产比率:流动资产比率是指企业流动资产与总资产的比例,反映了企业流动性的程度。
-
现金资产比率:现金资产比率是指企业现金资产与总资产的比例,反映了企业现金储备的情况。
-
固定资产比率:固定资产比率是指企业固定资产与总资产的比例,反映了企业固定资产在总资产中的占比。
-
有形资产比率:有形资产比率是指企业有形资产与总资产的比例,有形资产指的是可以触摸和看到的资产,如土地、建筑物等。
-
无形资产比率:无形资产比率是指企业无形资产与总资产的比例,无形资产指的是无形的资产,如专利、商标等。
-
资产负债率:资产负债率是指企业负债总额与总资产的比例,反映了企业负债的程度。
-
管理费用率:管理费用率是指企业管理费用与营业收入的比例,反映了企业管理费用在营业收入中的占比。
-
销售费用率:销售费用率是指企业销售费用与营业收入的比例,反映了企业销售费用在营业收入中的占比。
-
归属于母公司净利润占比:归属于母公司净利润占比是指企业归属于母公司的净利润与净利润的比例,反映了母公司对净利润的占有程度。
-
主营业务利润占比:主营业务利润占比是指企业主营业务利润与净利润的比例,反映了主营业务对净利润的贡献程度。
-
董监高报告期报酬均值:董监高报告期报酬均值是指企业董事、监事和高级管理人员在报告期内的平均报酬水平。
3、选择董监高薪酬作为解释变量的理论逻辑分析
- 吴育辉(2010)以 2004—2008 年我国全部 A 股上研究对象,发现高管薪酬与公司 ROA 显著正相关。张燕红(2016)和蒋泽芳(2019)的研究结果也证明高管薪酬激励对企业经营业绩存在显著正向影响。
- [1] 吴育辉,吴世农.高管薪酬:激励还是自利[J].会计研究,2010(11):40-48+96-97.
- [2]张燕红.高管薪酬激励对企业绩效的影响[J].经济问题,2016(06):116-120.
- [3]蒋泽芳,陈祖英.高管薪酬、股权集中度与企业绩效[J].财会通讯,2019(18):64-68.
三、多元回归模型的参数估计、结果展示与分析
1、描述性统计分析
xVars =['流动资产比率', '现金资产比率', '固定资产比率', '有形资产比率', '无形资产比率','资产负债率', '管理费用率', '销售费用率', '归属于母公司净利润占比', '主营业务利润占比', '董监高报告期报酬均值']
yVar = ['总资产净利润率(ROA)A']
xyVars = yVar + xVars
perct = [0.005,0.01,0.02,0.03, 0.04, 0.05, 0.1,0.15,0.25]
perct += [1-a for a in perct]
perct += [0.5]
sorted(perct)
data1[xVars].describe(percentiles = perct)
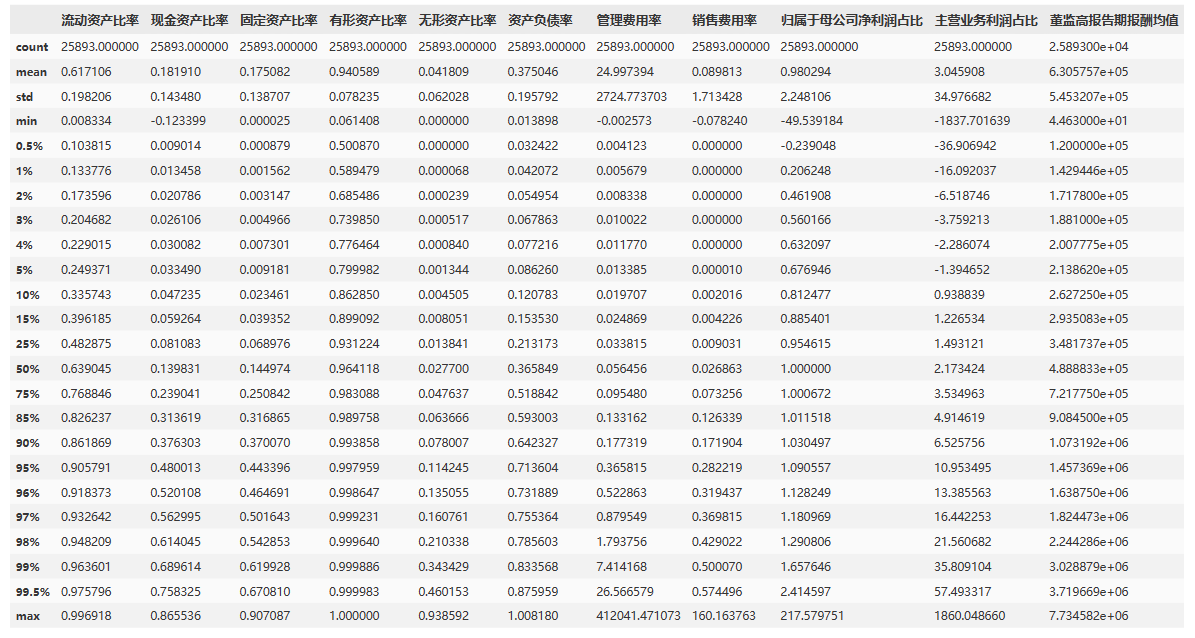
结合上面的描述性统计结果,可以看出:
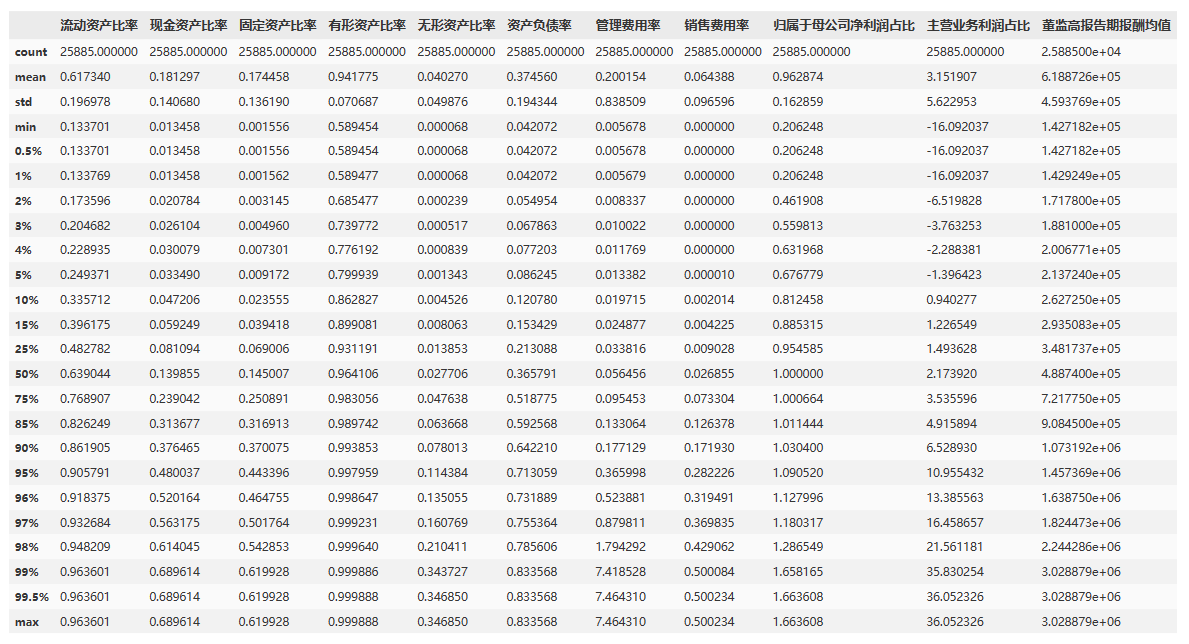
- 流动资产比率:流动资产比率最小值为0.008334,最大值为0.996918,中位数为0.639045。
- 现金资产比率:现金资产比率最小值为-0.123399,最大值为0.865536,中位数为0.139831。
- 固定资产比率:固定资产比率最小值为0.000025,最大值为0.907087,中位数为0.144974。
- 有形资产比率:有形资产比率最小值为0.061408,最大值为1,中位数为0.964118。
- 无形资产比率:无形资产比率最小值为0,最大值为0.938592,中位数为0.0277。
- 资产负债率:资产负债率最小值为0.013898,最大值为1.00818,中位数为0.365849。最大值接近1可能表示某些公司存在高度杠杆,这可能是金融机构的特点。因此,剔除上市公司当中的金融机构以减小金融机构对分析的影响。
- 管理费用率:管理费用率最小值为-0.002573,最大值为412041.4711,中位数为0.056456。
- 销售费用率:销售费用率最小值为-0.07824,最大值为160.163763,中位数为0.026863。
- 归属于母公司净利润占比:归属于母公司净利润占比最小值为-49.539184,最大值为217.579751,中位数为1。
- 主营业务利润占比:主营业务利润占比最小值为-1837.701639,最大值为1860.04866,中位数为2.173424。
- 董监高报告期报酬均值:董监高报告期报酬均值最小值为4.46E+01,最大值为7734582.353,中位数为4.89E+05。
2、剔除金融类上市公司
data1 = data1[~data1['股票简称'].str.contains('金融')]
data1
- 注:其实就减少了几条数据而已
3、对所有变量进行1%缩尾处理
cols_to_winsorize = ['流动资产比率', '现金资产比率', '固定资产比率', '有形资产比率', '无形资产比率','资产负债率', '管理费用率', '销售费用率', '归属于母公司净利润占比', '主营业务利润占比', '董监高报告期报酬均值']# 对每个变量进行缩尾处理
for col in cols_to_winsorize:data1[col] = winsorize(data1[col], limits=(0.01, 0.01))
data1[xVars].describe(percentiles = perct)
4、0-1标准化,所有解释变量
data1[xVars] = MinMaxScaler().fit_transform(data1[xVars])
data1[xVars].describe()
5、绘制热力图
import matplotlib.pyplot as plt
import seaborn as sns # 画热度图
plt.rcParams["font.sans-serif"] = ["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"] = False #该语句解决图像中的“-”负号的乱码问题
a = data1[xVars].corr()
plt.figure(figsize=(10, 8)) # 调整图的大小为10x8
sns.heatmap(a, vmin=-1, vmax=1, annot=True, fmt=".2f", cmap="coolwarm", annot_kws={"size": 12, "color": "red"})
plt.show()
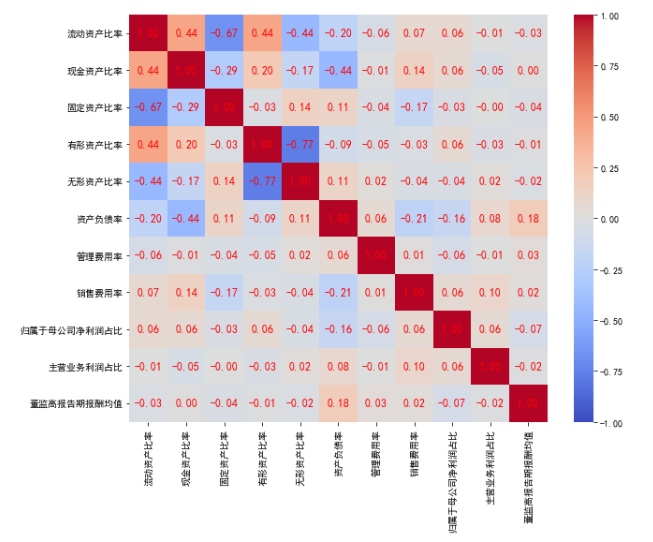
从解释变量之间的相关性分析可以看出:解释变量中(正/负)高相关性的变量需要从解释变量剔除
- “有形资产比率”与“无形资产比率”的相关系数为-0.77,考虑保留“无形资产比率”,同时删除“有形资产比率”
- “流动资产比率”与“固定资产比率”的相关系数为-0.67,考虑保留“流动形资产比率”,同时删除“固定资产比率”
xVars =['流动资产比率', '现金资产比率', '无形资产比率','资产负债率', '管理费用率', '销售费用率', '归属于母公司净利润占比', '主营业务利润占比', '董监高报告期报酬均值']
xd = data1[xVars]
xdcons = sma.add_constant(xd)
yd = data1[yVar]
# 参数估计
model = sma.OLS(yd, xdcons).fit()
model.summary2().tables[1]
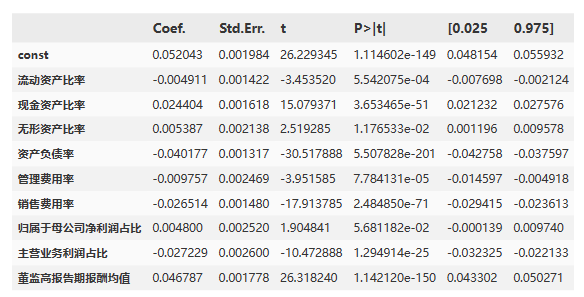
根据给出的回归系数和统计显著性水平,对每个解释变量进行分析:
-
流动资产比率(Coefficient: -0.004911, P-value: 0.000554):流动资产比率的增加与因变量的减少呈负相关关系,且统计上显著。
-
现金资产比率(Coefficient: 0.024404, P-value: 3.653465e-51):现金资产比率的增加与因变量的增加呈正相关关系,且统计上显著。
-
无形资产比率(Coefficient: 0.005387, P-value: 0.011765):无形资产比率的增加与因变量的增加呈正相关关系,但统计上显著性较低。
-
资产负债率(Coefficient: -0.040177, P-value: 5.507828e-201):资产负债率的增加与因变量的减少呈负相关关系,且统计上显著。
-
管理费用率(Coefficient: -0.009757, P-value: 7.784131e-05):管理费用率的增加与因变量的减少呈负相关关系,且统计上显著。
-
销售费用率(Coefficient: -0.026514, P-value: 2.484850e-71):销售费用率的增加与因变量的减少呈负相关关系,且统计上显著。
-
归属于母公司净利润占比(Coefficient: 0.004800, P-value: 0.056812):归属于母公司净利润占比的增加与因变量的增加呈正相关关系,但统计上显著性较低。
-
主营业务利润占比(Coefficient: -0.027229, P-value: 1.294914e-25):主营业务利润占比的增加与因变量的减少呈负相关关系,且统计上显著。
-
董监高报告期报酬均值(Coefficient: 0.046787, P-value: 1.142120e-150):董监高报告期报酬均值的增加与因变量的增加呈正相关关系,且统计上显著。
-
结论:流动资产比率、资产负债率、管理费用率、销售费用率和主营业务利润占比对因变量有显著影响,而现金资产比率、无形资产比率、归属于母公司净利润占比和董监高报告期报酬均值对因变量的影响可能较弱。
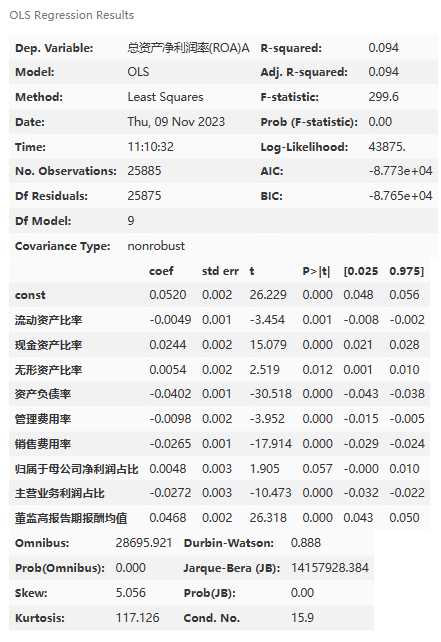
model.summary()
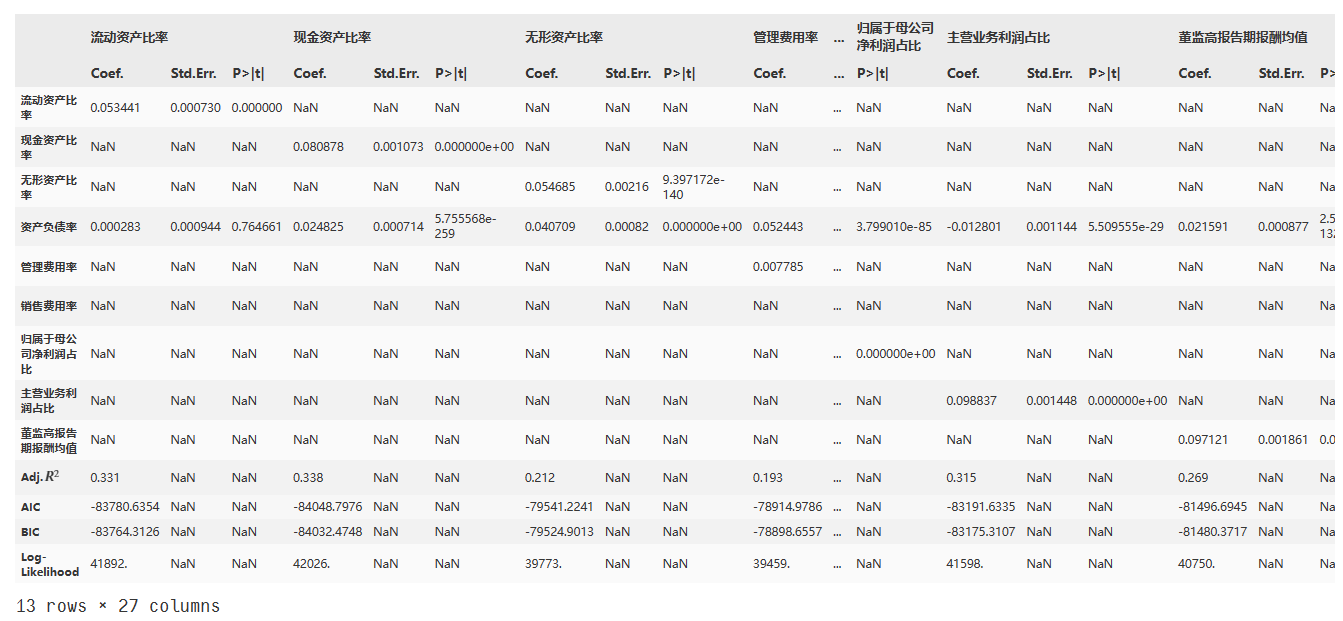
6、逐步加入关键解释变量
# 需要逐步加入的变量
xStepVars = ['流动资产比率', '现金资产比率', '无形资产比率', '管理费用率', '销售费用率', '归属于母公司净利润占比', '主营业务利润占比', '董监高报告期报酬均值']# 始终保留的变量(控制变量)
x0Vars = ['资产负债率']sts = ['Coef.', 'Std.Err.', 'P>|t|']
dst = ['Adj.$R^2$', 'AIC', 'BIC','Log-Likelihood']
step_res = pd.DataFrame(columns = pd.MultiIndex.from_product([xStepVars + ['整体回归'], sts]), # 最后加上一列,全部变量的整体回归index = xVars + dst )
for xsv in xStepVars:xns = [xsv] + x0Varsres = sma.OLS(yd, xdcons[xns]).fit()t_res = res.summary2().tables[1]t_res = t_res[sts]step_res[xsv] = t_res# 取出诊断统计量,放在 Coef. 列t_res = res.summary2().tables[0] for i in range(len(dst)):step_res[xsv, 'Coef.'][dst[i]] = t_res.iloc[i,3]# print(dst[i], ' = ', t_res.iloc[i + 1,3], '填充后 ', step_res[xsv, 'Coef.'][dst[i]])# 全部变量的整体回归结果
res = sma.OLS(yd, xdcons[xStepVars + x0Vars]).fit()
t_res = res.summary2().tables[1] # 取出系数估计结果
step_res['整体回归'] = t_res[sts] # 自动按照 index 匹配赋值# 取出诊断统计量,放在 Coef. 列
t_res = res.summary2().tables[0]
for i in range(len(dst)):step_res['整体回归', 'Coef.'][dst[i]] = t_res.iloc[i,3]
step_res
7、制作显著性表格
# 制作显著性表格
df = step_res
rows = df.indexdfres = pd.DataFrame(index = rows, columns = xStepVars + ['整体回归'])for xsv in xStepVars + ['整体回归']:coef = df[xsv].astype(float)['Coef.'].map(lambda x: '' if np.isnan(x) else ('%.3f') % x )pvs = df[xsv]['P>|t|'].map(lambda x: '***' if x<=0.01 else '**' if x<=0.05 else '*' if x<=0.1 else '')dfres[xsv] = coef + pvs
dfres.loc['Adj.$R^2$',:] = dfres.loc['Adj.$R^2$',:].map(lambda x: '' if np.isnan(float(x)) else ('%.3f%%') % (float(x)*100) )
dfres
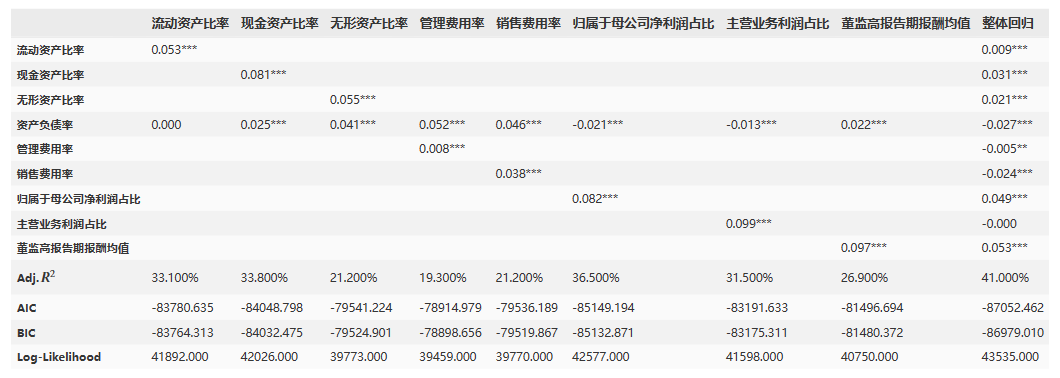
由上述显著性表格可知:
-
流动资产比率:流动资产比率与整体回归呈显著正相关。
-
现金资产比率:现金资产比率与整体回归呈显著正相关。
-
无形资产比率:无形资产比率与整体回归呈显著正相关。
-
资产负债率:资产负债率与整体回归呈显著负相关。
-
管理费用率:管理费用率与整体回归呈显著负相关。
-
销售费用率:销售费用率与整体回归呈显著负相关。
-
归属于母公司净利润占比:归属于母公司净利润占比与整体回归呈显著正相关。
-
主营业务利润占比:主营业务利润占比与整体回归呈显著正相关。
-
董监高报告期报酬均值:董监高报告期报酬均值与整体回归呈显著正相关。
8、经典logit回归
# 将因变量归一化
yd = MinMaxScaler().fit_transform(yd)
import statsmodels.api as sma# 将自变量和因变量赋值给Xbs和ybs
Xbs = xdcons[xStepVars + x0Vars]
ybs = yd# 为自变量添加常数列
Xbs_cons = sma.add_constant(Xbs)# 创建logit回归模型并拟合
lr = sma.Logit(ybs, Xbs_cons)
logit_res = lr.fit(method='lbfgs', maxiter=500)# 打印logit回归结果
logit_res.summary()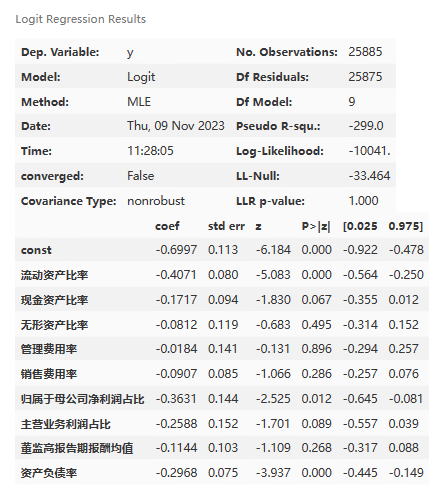
描述:
- No. Observations: 25885 - 观测样本的数量是25885。
- Model: Logit - 使用的模型是逻辑回归模型。
- Df Residuals: 25875 - 残差的自由度是25875。
- Method: MLE - 使用的估计方法是最大似然估计。
- Df Model: 9 - 模型的自由度是9,表示有9个自变量。
- Pseudo R-squ.: -299.0 - 伪R平方值为-299.0,表示模型拟合效果较差。 Time: 11:28:05 - 模型拟合的时间是上午11:28:05。
- Log-Likelihood: -10041. - 对数似然值为-10041.,表示模型的对数似然函数值。
- converged: False - 模型是否收敛,False表示模型未收敛。
- LL-Null: -33.464 - 空模型的对数似然值为-33.464。
- Covariance Type: nonrobust - 协方差类型为非鲁棒性。
- LLR p-value: 1.000 - 对数似然比检验的p值为1.000,表示模型的拟合效果不显著。
lr = sma.Logit(ybs, Xbs_cons)
# logit_res = lr.fit(method = 'lbfgs', maxiter = 500)
logit_res = lr.fit_regularized(method = 'l1', maxiter = 500, alpha = 1, trim_mode = 'size')
logit_res.summary()
res = logit_res.summary2().tables[1]
logit_res.summary2().tables[0]
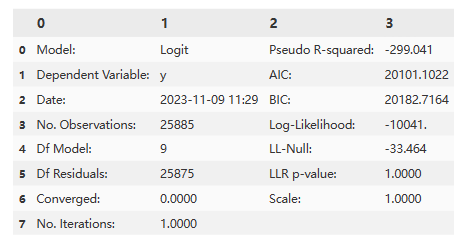
round(res.loc[xVars,:],4)
相关文章:

【Python】上市公司数据进行经典OLS回归实操
一、题目二、数据合并、清洗、描述性统计1、数据获取2、数据合并3、选择董监高薪酬作为解释变量的理论逻辑分析 三、多元回归模型的参数估计、结果展示与分析1、描述性统计分析2、剔除金融类上市公司3、对所有变量进行1%缩尾处理4、0-1标准化,所有解释变量5、绘制热…...
科研学习|科研软件——有序多分类Logistic回归的SPSS教程!
一、问题与数据 研究者想调查人们对“本国税收过高”的赞同程度:Strongly Disagree——非常不同意,用“0”表示;Disagree——不同意,用“1”表示;Agree--同意,用“2”表示;Strongly Agree--非常…...
微服务简单理解与快速搭建
分布式和微服务 含义 微服务架构 微服务架构风格是一种将一个单一应用程序开发为一组小型服务的方法,每个服务运行在自己的进程中,服务间通信采用轻量级通信机制(通常用HTTP资源API)。这些服务围绕业务能力构建并且可通过全自动部署机制独立部署。这些服…...

QColorDialog开发实例
文章目录 一、QColorDialog基本用法:二、QColorDialog详解三、QColorDialog接口说明静态函数成员函数 四、QColorDialog代码开发实例 QColorDialog 是 Qt 框架中用于选择颜色的对话框类。它提供了一个用户友好的界面,允许用户选择颜色。以下是 QColorDi…...

linux实现全局快捷键
文章目录 第一步:加载KF5GlobalAccel库第二步:代码实现2.1 定义一个QAction2.2 KGlobalAccel::self()注册快捷键3 源码地址有一个需求,就是在应用在后台运行时,用户可以通过快捷键将应用唤起。或者应用响应。 其实就是全局快捷键的功能。 这个功能利用了linux操作系统中的d…...

共享台球室小程序系统:智能化预约与管理
在当今数字化的时代,共享经济模式已经渗透到各个领域。其中,共享台球室作为一个结合了传统与现代元素的项目,越来越受到年轻人的喜爱。为了满足市场需求,我们设计了一款基于微信小程序的共享台球室预约与管理系统,通过…...
百度文心一言
1分钟了解一言是谁? 一句话介绍【文心一言】 我是百度研发的人工智能模型,任何人都可以通过输入【指令】和我进行互动,对我提出问题或要求,我能高效地帮助你们获取信息、知识和灵感哦 什么是指令?我该怎么和你互动&am…...

225.用队列实现栈(LeetCode)
思路 思路:用两个队列实现栈后进先出的特性 ,两个队列为空时,先将数据都导向其中一个队列。 当要模拟出栈时,将前面的元素都导入另一个空队列,再将最后一个元素移出队列 实现 实现: 因为C语言没有库可以…...
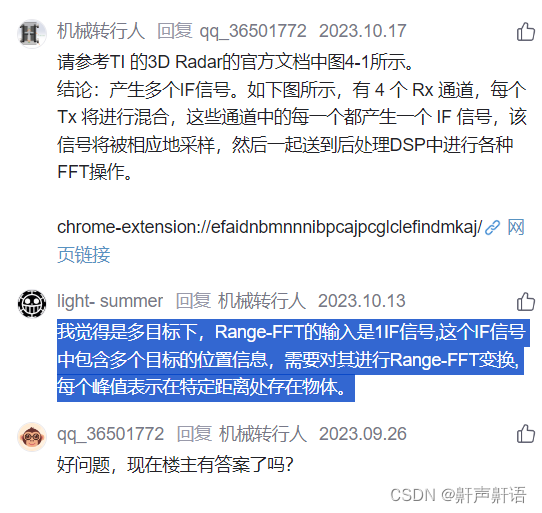
汽车FMCW毫米波雷达信号处理流程(推荐---基础详细---清楚的讲解了雷达的过程---强烈推荐)
毫米波雷达在进行多目标检测时,TX发射一个Chirp,在不同距离下RX会接收到多个反射Chirp信号(仅以单个chirp为例)。 雷达通过接收不同物体的发射信号,并转为IF信号,利用傅里叶变换将产生一个具有不同的分离峰值的频谱,每个峰值表示在特定距离处存在物体。 请问,这种多目标…...
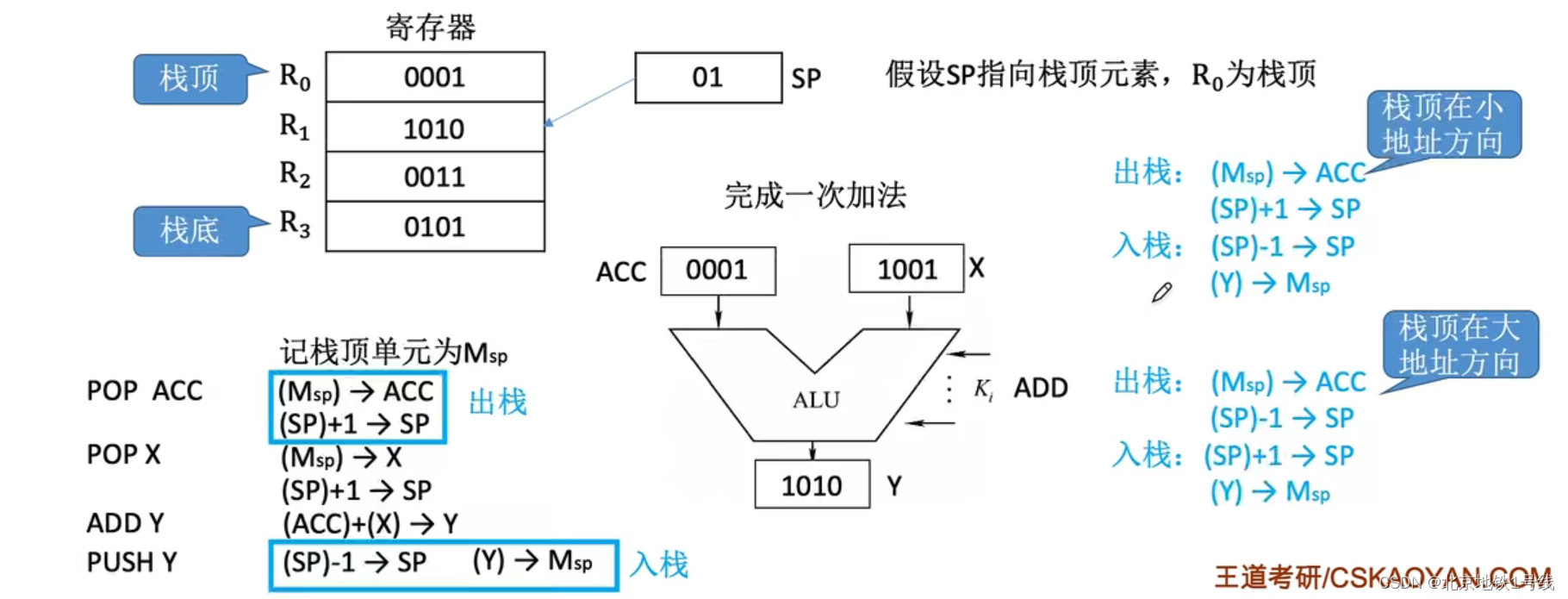
8.指令格式,指令的寻址方式
目录 一. 指令格式 二. 扩展操作码 三. 指令寻址 (1)指令寻址 (2)数据寻址 1.直接寻址 2.间接寻址 3.寄存器寻址 4.寄存器间接寻址 5.隐含寻址 6.立即寻址 7.基址寻址 8.变址寻址 9.相对寻址 10.堆栈寻址 一. 指令…...
k8s自定义Endpoint实现内部pod访问外部应用
自定义endpoint实现内部pod访问外部应用 endpoint除了可以暴露pod的IP和端口还可以代理到外部的ip和端口 使用场景 公司业务还还没有完成上云, 一部分云原生的,一部分是实体的 业务上云期间逐步实现上云,保证各个模块之间的解耦性 比如使…...
)
[100天算法】-分割等和子集(day 78)
题目描述 给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。注意:每个数组中的元素不会超过 100 数组的大小不会超过 200 示例 1:输入: [1, 5, 11, 5]输出: true解释: 数组可以分割成 [1, 5, 5] 和 [11].示例 2:输入:…...

共享台球室小程序系统的数据统计与分析功能
随着共享经济的繁荣发展,共享台球室作为一种新型的娱乐方式,越来越受到年轻人的喜爱。为了更好地满足用户需求和提高管理效率,我们设计了一款基于微信小程序的共享台球室预订与管理系统。该系统不仅具备基本的预订和管理功能,还集…...
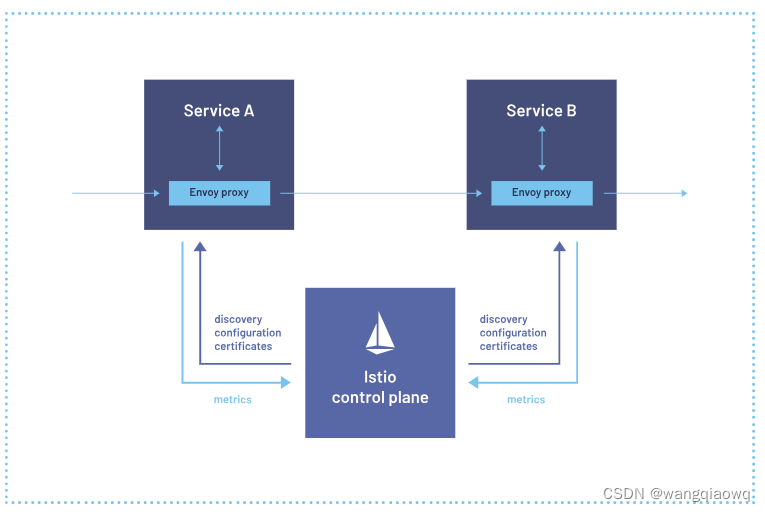
Istio学习笔记- 服务网格
Istio 服务网格 参考:Istio / Istio 服务网格 Istio 使用功能强大的 Envoy 服务代理扩展了 Kubernetes,以建立一个可编程的、可感知的应用程序网络。Istio 与 Kubernetes 和传统工作负载一起使用,为复杂的部署带来了标准的通用流量管理、遥…...

离散卡尔曼滤波器算法详解及重要参数(Q、R、P)的讨论
公开数据集中文版详细描述参考前文:https://editor.csdn.net/md/?not_checkout1&spm1011.2124.3001.6192神经元Spike信号分析参考前文:https://blog.csdn.net/qq_43811536/article/details/134359566?spm1001.2014.3001.5501神经元运动调制分析参考…...

伊朗黑客对以色列科技行业发起恶意软件攻击
最近,安全研究人员发现了一场由“Imperial Kitten”发起的新攻击活动,目标是运输、物流和科技公司。 “Imperial Kitten”又被称为“Tortoiseshell”、“TA456”、“Crimson Sandstorm”和“Yellow Liderc”,多年来一直使用“Marcella Flore…...

selenium报错:没有打开网页或selenium.common.exceptions.NoSuchDriverException
文章目录 问题解决方法 问题 当selenium的环境配置没有问题,但在使用selenium访问浏览器时并没有打开网页,或者出现selenium.common.exceptions.NoSuchDriverException报错信息(如下图所示)。 以上问题可能的原因是没有配置chrom…...

Java开源工具库使用之线上监控诊断库Arthas
文章目录 前言一、介绍1.1 功能1.2 原理 二、安装使用2.1 下载2.2 使用 三、常用3.1 实时查看3.2 追踪查看3.3 辅助命令3.4 热更新3.5 监控 四、实战4.1 CPU/内存占用过高4.2 接口耗时高4.3 找到类所在jar4.4 查找类的实例4.5 生成火焰图 参考 前言 在现代软件开发中ÿ…...
Nodejs操作缓存数据库-Redis
Hi I’m Shendi Nodejs专栏 Nodejs操作缓存数据库-Redis 在服务端开发中,缓存数据库也是不可或缺的,可以提高程序并发以及方便后续扩展,而目前最常用的莫过于Redis了 安装依赖 和之前的mysql一样,redis的依赖最常用的就是redis …...

Springboot项目全局异常处理
1.ErrorCode.java package com.hng.config.exception.error;/*** Author: 郝南过* Description: TODO* Date: 2023/11/14 10:56* Version: 1.0*/ public interface ErrorCode {String getCode();String getMessage(); }2.ErrorEnum.java package com.hng.config.exception.er…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
