C#,数值计算——函数计算,Ratfn的计算方法与源程序

1 文本格式
using System;
namespace Legalsoft.Truffer
{
public class Ratfn
{
private double[] cofs { get; set; }
private int nn { get; set; }
private int dd { get; set; }
public Ratfn(double[] num, double[] den)
{
this.cofs = new double[num.Length + den.Length - 1];
this.nn = num.Length;
this.dd = den.Length;
for (int j = 0; j < nn; j++)
{
cofs[j] = num[j] / den[0];
}
for (int j = 1; j < dd; j++)
{
cofs[j + nn - 1] = den[j] / den[0];
}
}
public Ratfn(double[] coffs, int n, int d)
{
this.cofs = Globals.CopyFrom(coffs);
this.nn = n;
this.dd = d;
}
public double get(double x)
{
double sumn = 0.0;
double sumd = 0.0;
for (int j = nn - 1; j >= 0; j--)
{
sumn = sumn * x + cofs[j];
}
for (int j = nn + dd - 2; j >= nn; j--)
{
sumd = sumd * x + cofs[j];
}
return sumn / (1.0 + x * sumd);
}
public static Ratfn pade(double[] cof)
{
int n = (cof.Length - 1) / 2;
double[,] q = new double[n, n];
double[,] qlu = new double[n, n];
double[] x = new double[n];
double[] y = new double[n];
for (int j = 0; j < n; j++)
{
y[j] = cof[n + j + 1];
for (int k = 0; k < n; k++)
{
q[j, k] = cof[j - k + n];
}
}
LUdcmp lu = new LUdcmp(q);
lu.solve( y, x);
for (int j = 0; j < 4; j++)
{
lu.mprove(y, x);
}
for (int k = 0; k < n; k++)
{
double sum = cof[k + 1];
for (int j = 0; j <= k; j++)
{
sum -= x[j] * cof[k - j];
}
y[k] = sum;
}
double[] num = new double[n + 1];
double[] denom = new double[n + 1];
num[0] = cof[0];
denom[0] = 1.0;
for (int j = 0; j < n; j++)
{
num[j + 1] = y[j];
denom[j + 1] = -x[j];
}
return new Ratfn(num, denom);
}
public static Ratfn ratlsq(UniVarRealValueFun fn, double a, double b, int mm, int kk, ref double dev)
{
const int NPFAC = 8;
const int MAXIT = 5;
const double BIG = 1.0e99;
const double PIO2 = 1.570796326794896619;
int ncof = mm + kk + 1;
int npt = NPFAC * ncof;
double[] bb = new double[npt];
double[] coff = new double[ncof];
double[] ee = new double[npt];
double[] fs = new double[npt];
double[] wt = new double[npt];
double[] xs = new double[npt];
double[,] u = new double[npt, ncof];
Ratfn ratbest = new Ratfn(coff, mm + 1, kk + 1);
dev = BIG;
for (int i = 0; i < npt; i++)
{
if (i < (npt / 2) - 1)
{
double hth = PIO2 * i / (npt - 1.0);
xs[i] = a + (b - a) * Globals.SQR(Math.Sin(hth));
}
else
{
double hth = PIO2 * (npt - i) / (npt - 1.0);
xs[i] = b - (b - a) * Globals.SQR(Math.Sin(hth));
}
fs[i] = fn.funk(xs[i]);
wt[i] = 1.0;
ee[i] = 1.0;
}
double e = 0.0;
for (int it = 0; it < MAXIT; it++)
{
for (int i = 0; i < npt; i++)
{
double power = wt[i];
bb[i] = power * (fs[i] + Globals.SIGN(e, ee[i]));
for (int j = 0; j < mm + 1; j++)
{
u[i, j] = power;
power *= xs[i];
}
power = -bb[i];
for (int j = mm + 1; j < ncof; j++)
{
power *= xs[i];
u[i, j] = power;
}
}
SVD svd = new SVD(u);
svd.solve(bb, coff);
double devmax = 0.0;
double sum = 0.0;
Ratfn rat = new Ratfn(coff, mm + 1, kk + 1);
for (int j = 0; j < npt; j++)
{
ee[j] = rat.get(xs[j]) - fs[j];
wt[j] = Math.Abs(ee[j]);
sum += wt[j];
if (wt[j] > devmax)
{
devmax = wt[j];
}
}
e = sum / npt;
if (devmax <= dev)
{
ratbest = rat;
//ratbest.CopyFrom(rat);
dev = devmax;
}
//Console.Write(" ratlsq iteration= ");
//Console.Write(it);
//Console.Write(" max error= ");
//Console.Write("{0,10}", devmax);
//Console.Write("{0}", "\n");
}
return ratbest;
}
}
}
2 代码格式
using System;namespace Legalsoft.Truffer
{public class Ratfn{private double[] cofs { get; set; }private int nn { get; set; }private int dd { get; set; }public Ratfn(double[] num, double[] den){this.cofs = new double[num.Length + den.Length - 1];this.nn = num.Length;this.dd = den.Length;for (int j = 0; j < nn; j++){cofs[j] = num[j] / den[0];}for (int j = 1; j < dd; j++){cofs[j + nn - 1] = den[j] / den[0];}}public Ratfn(double[] coffs, int n, int d){this.cofs = Globals.CopyFrom(coffs);this.nn = n;this.dd = d;}public double get(double x){double sumn = 0.0;double sumd = 0.0;for (int j = nn - 1; j >= 0; j--){sumn = sumn * x + cofs[j];}for (int j = nn + dd - 2; j >= nn; j--){sumd = sumd * x + cofs[j];}return sumn / (1.0 + x * sumd);}public static Ratfn pade(double[] cof){int n = (cof.Length - 1) / 2;double[,] q = new double[n, n];double[,] qlu = new double[n, n];double[] x = new double[n];double[] y = new double[n];for (int j = 0; j < n; j++){y[j] = cof[n + j + 1];for (int k = 0; k < n; k++){q[j, k] = cof[j - k + n];}}LUdcmp lu = new LUdcmp(q);lu.solve( y, x);for (int j = 0; j < 4; j++){lu.mprove(y, x);}for (int k = 0; k < n; k++){double sum = cof[k + 1];for (int j = 0; j <= k; j++){sum -= x[j] * cof[k - j];}y[k] = sum;}double[] num = new double[n + 1];double[] denom = new double[n + 1];num[0] = cof[0];denom[0] = 1.0;for (int j = 0; j < n; j++){num[j + 1] = y[j];denom[j + 1] = -x[j];}return new Ratfn(num, denom);}public static Ratfn ratlsq(UniVarRealValueFun fn, double a, double b, int mm, int kk, ref double dev){const int NPFAC = 8;const int MAXIT = 5;const double BIG = 1.0e99;const double PIO2 = 1.570796326794896619;int ncof = mm + kk + 1;int npt = NPFAC * ncof;double[] bb = new double[npt];double[] coff = new double[ncof];double[] ee = new double[npt];double[] fs = new double[npt];double[] wt = new double[npt];double[] xs = new double[npt];double[,] u = new double[npt, ncof];Ratfn ratbest = new Ratfn(coff, mm + 1, kk + 1);dev = BIG;for (int i = 0; i < npt; i++){if (i < (npt / 2) - 1){double hth = PIO2 * i / (npt - 1.0);xs[i] = a + (b - a) * Globals.SQR(Math.Sin(hth));}else{double hth = PIO2 * (npt - i) / (npt - 1.0);xs[i] = b - (b - a) * Globals.SQR(Math.Sin(hth));}fs[i] = fn.funk(xs[i]);wt[i] = 1.0;ee[i] = 1.0;}double e = 0.0;for (int it = 0; it < MAXIT; it++){for (int i = 0; i < npt; i++){double power = wt[i];bb[i] = power * (fs[i] + Globals.SIGN(e, ee[i]));for (int j = 0; j < mm + 1; j++){u[i, j] = power;power *= xs[i];}power = -bb[i];for (int j = mm + 1; j < ncof; j++){power *= xs[i];u[i, j] = power;}}SVD svd = new SVD(u);svd.solve(bb, coff);double devmax = 0.0;double sum = 0.0;Ratfn rat = new Ratfn(coff, mm + 1, kk + 1);for (int j = 0; j < npt; j++){ee[j] = rat.get(xs[j]) - fs[j];wt[j] = Math.Abs(ee[j]);sum += wt[j];if (wt[j] > devmax){devmax = wt[j];}}e = sum / npt;if (devmax <= dev){ratbest = rat;//ratbest.CopyFrom(rat);dev = devmax;}//Console.Write(" ratlsq iteration= ");//Console.Write(it);//Console.Write(" max error= ");//Console.Write("{0,10}", devmax);//Console.Write("{0}", "\n");}return ratbest;}}
}
相关文章:

C#,数值计算——函数计算,Ratfn的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { public class Ratfn { private double[] cofs { get; set; } private int nn { get; set; } private int dd { get; set; } public Ratfn(double[] num, double[] den) { …...

排序算法之-快速
算法原理 丛待排序的数列中选择一个基准值,通过遍历数列,将数列分成两个子数列:小于基准值数列、大于基准值数列,准确来说还有个子数列:等于基准值即: 算法图解 选出基准元素pivot(可以选择…...

[vim]Python编写插件学习笔记2 - 分离
0 环境 Windows 11 22H2gVim82 (D:/ProgramFiles/Vim)Python311 (D:/ProgramFiles/Python311)Vundle v0.10.2 阅读本文前,需要先了解前文: 《[vim]Python 编写插件学习笔记1 - 开始》 1 Python 与 vimscript 分离 前文编写 vim 插件的方式,是将 Pyt…...

【已解决】ModuleNotFoundError: No module named ‘kornia‘
问题描述 Traceback (most recent call last): File "main.py", line 47, in <module> import data_augmentation File "/media/visionx/monica/project/stable_signature/hidden/data_augmentation.py", line 15, in <module> im…...
预览PDF并显示当前页数
这里写目录标题 步骤实例实例效果图 步骤 1.安装依赖 npm install --save vue-pdf2.在需要的页面,引入插件 import pdf from vue-pdf3.使用 单页pdf可以直接使用 <pdf :src"获取到的pdf地址"></pdf>多页pdf通过循环实现 html标签部分 &l…...
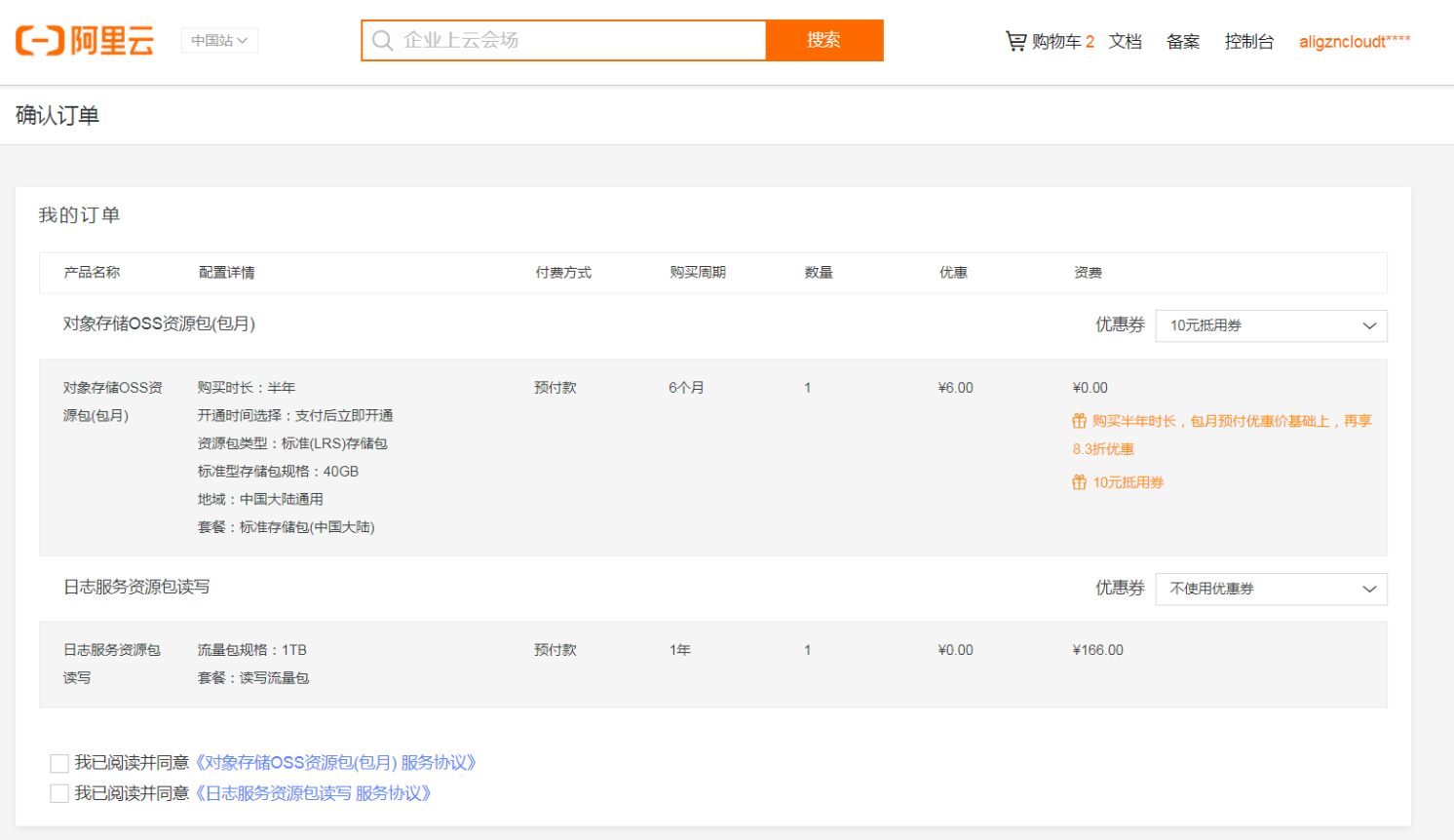
阿里云优惠券介绍、作用、领取入口及使用教程
阿里云是阿里巴巴集团倾力打造的云计算品牌,提供丰富多样的云计算产品及服务,为了吸引用户,阿里云经常推出各种优惠活动,其中就包括阿里云优惠券的发放。本文将为大家详细介绍阿里云优惠券的作用、领取入口以及使用教程。 一、阿里…...

Shell编程--流程控制
目录 1.条件结构1.1.文件测试(字符串)1.2.字符串比较1.3.数字条件比较1.4.文件条件判断 2.if多条件判断3.case语句 1.条件结构 测试:test 条件 条件为真返回 0,条件为假返回 1 语法:[ 条件 ] test 条件能够理解以下类型的表达式 1.1.…...
)
设计模式-模板方法模式(Template Method)
设计模式-模板方法模式(Template Method) 一、模板方法模式概述1.1 什么是模板方法模式1.2 简单实现模板方法模式1.3 使用模板方法模式的注意事项 二、模板方法模式的用途三、模板方法模式实现方式3.1 抽象类中定义模板方法,子类实现具体方法…...
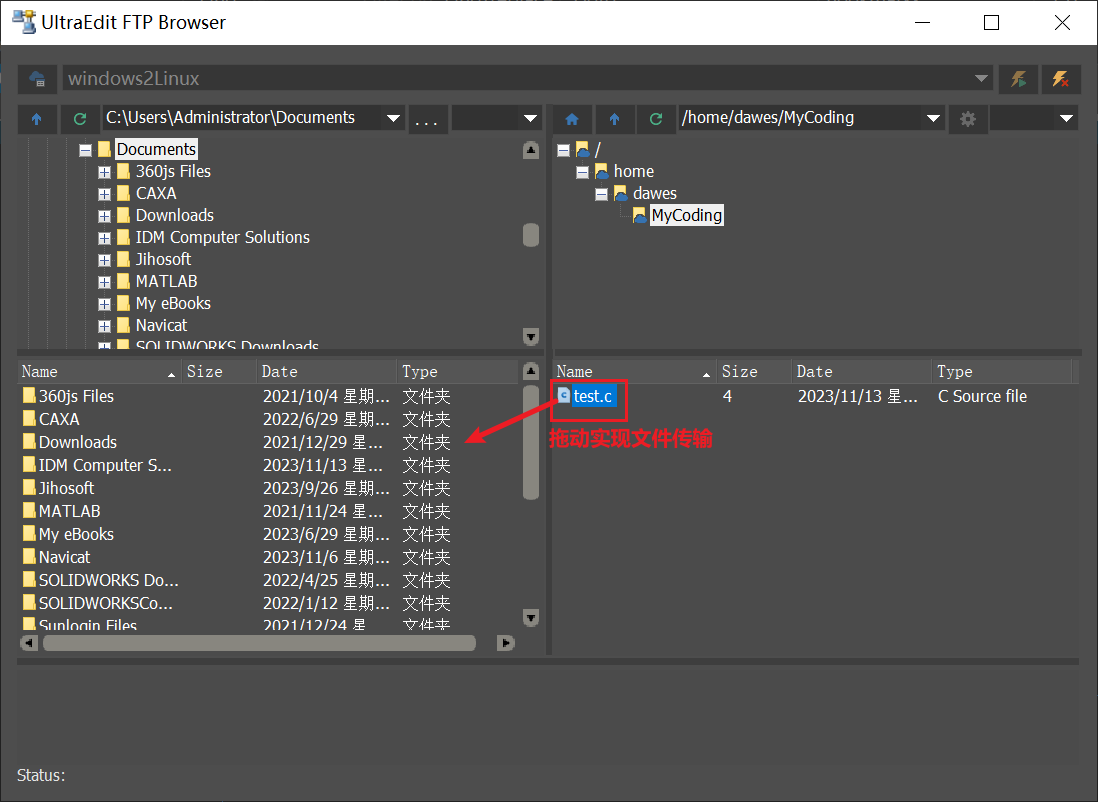
远程登录Linux方法(Linux平台相互远程;Windows远程登录Linux、远程编码、文件传输;无法远程登录的问题解决;c程序的编译)
在实际使用Linux系统过程中我们不可避免的需要远程登录Linux,这是因为未来大家使用Linux服务器的时候你所对应的那台Linux服务器不一定提供界面(服务器可能在外地)。本篇将会介绍远程登录Linux的方法。 文章目录 1. SSH介绍2. Linux平台相互远程及文件传输2.1 Linux…...

macOS 13.6 及后续系统安装 Asahi Linux 将破坏引导
导读Asahi Linux 是一个致力于为 Apple Silicon 设备带来 Linux 支持的项目,日前有用户反馈称,若在相关设备上安装了 macOS 13.6-14,再安装 Asahi Linux ,就会导致系统引导失败,出现“黑屏”情况。 目前 Asahi Linux 项…...
Python武器库开发-flask篇之flask框架的安装(二十一)
Flask介绍 Flask是一个基于Python开发并且依赖jinja2模板和Werkzeug WSGI服务的一个微型框架,对于Werkzeug本质是Socket服务端,其用于接收http请求并对请求进行预处理,然后触发Flask框架,开发人员基于Flask框架提供的功能对请求进…...

【CASS精品教程】打开cass提示base.dcl未找到文件的解决办法
打开cass 7.1时提示base.dcl未找到文件的解决办法。 文章目录 一、问题描述二、解决办法 一、问题描述 系统上安装了cad2006cass7.1,cass软件可以正常打开,但是在使用屏幕菜单绘制地图时,选择一个工具,提示base.dcl未找到文件&am…...

[vim]Python编写插件学习笔记3 - 命令行参数
0 环境 Windows 11 22H2gVim82 (D:/ProgramFiles/Vim)Python311 (D:/ProgramFiles/Python311)Vundle v0.10.2 阅读本文前,需要先了解前文: 《[vim]Python 编写插件学习笔记1 - 开始》 《[vim]Python 编写插件学习笔记2 - 分离》 1 前提说明 由于本…...

【仙逆】王林400年晋升元婴,复仇藤化元杀尽藤姓,高老畏罪自裁
Hello,小伙伴们,我是小郑继续为大家深度解析国漫资讯。 深度爆料仙逆第10集剧情解析,高启明,缥缈宗的元婴初期老祖,一生潜心研究推演之术,洞察先机,乃是宗门之人的精神支柱。藤化元曾为寻找王林父母所在之…...
云原生实战课大纲
1. 云原生是什么 原生应用(java,pyrhon) 上云的过程应用上云遇到的问题1.微服务的拆分 微服务的访问关系应用的架构云原生适合什么样的人去学具备什么样的前提条件云原生要学习什么docker k8s devlops server mesh jks k8s监控吧自己的微服务部署上…...

数据湖架构
数据湖架构介绍 数据湖(Data Lake)是一个存储大量结构化和非结构化数据的集中式数据存储库。 与传统的数据仓库不同,数据湖采用扁平化结构,将数据存储在原始形式下,不需要进行预处理或转化。这使得数据湖能够同时支持…...
Zabbix 5.0部署(centos7+server+MySQL+Apache)
环境 系统IPZABBIX版本主机名centos7192.168.231.2195.0zabbix-server 安装zabbix 我选择版本是zabbix-5.0 zabbix的官网是Zabbix :: The Enterprise-Class Open Source Network Monitoring Solution 安装Zabbix软件源 rpm -Uvh https://repo.zabbix.com/zabbix/5.0/rhel/7/…...
YOLO改进系列之注意力机制(CloAttention模型介绍)
CloAttention来自清华大学的团队提出的一篇论文CloFormer,作者从频域编码的角度认为现有的轻量级视觉Transformer中,大多数方法都只关注设计稀疏注意力,来有效地处理低频全局信息,而使用相对简单的方法处理高频局部信息。很少有方…...
)
openssl+AES开发实例(linux)
文章目录 一、AES介绍二、AES原理三、AES开发实例 一、AES介绍 AES(Advanced Encryption Standard)是一种对称密钥加密标准,它是一种对称加密算法,意味着相同的密钥用于加密和解密数据。AES 是 NIST(美国国家标准与技…...

FreeRTOS源码阅读笔记3--queue.c
消息队列可以应用于发送不定长消息的场合,包括任务与任务间的消息交换,队列是 FreeRTOS 主要的任务间通讯方式,可以在任务与任务间、中断和任务间传送信息,发送到 队列的消息是通过拷贝方式实现的,这意味着队列存储…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
