【分布式】CAP理论详解
一、CAP理论概述
在分布式系统中,CAP是指一组原则,它们描述了在网络分区(Partition)时,分布式系统能够提供的保证。CAP代表Consistency(一致性)、Availability(可用性)和Partition Tolerance(分区容错性)。
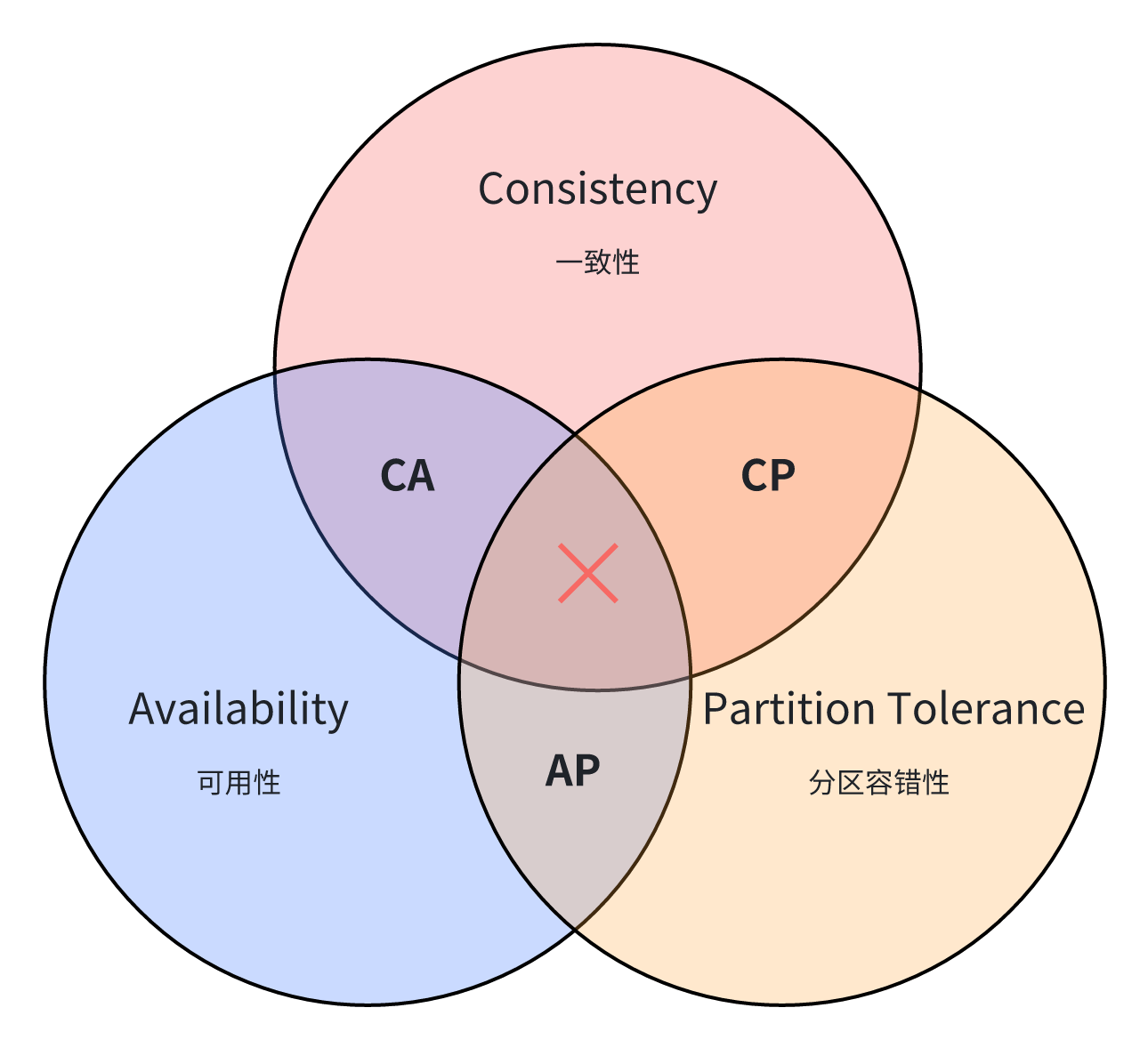
麻省理工学院的 Seth Gilbert 和 Nancy Lynch 以严谨的数学推理证明了 CAP 猜想。自此,CAP 正式从猜想变为分布式计算领域所公认的著名定理。这个定理里描述了一个分布式的系统中,涉及共享数据问题时,以下三个特性最多只能同时满足其中两个。
1.1、一致性(Consistency)
一致性(Consistency):代表数据在任何时刻、任何分布式节点中所看到的都是符合预期的。
简单来说,写入数据到分布式系统的某一个节点后,操作会立刻反应到整个分布式系统上。即任何时刻从任意一个节点读取的数据都必须是一样的。
要实现一致性,那么需要保证:当在分布式系统更新一个节点的数据时候,分布式系统会立马把这个数据同步到所有的节点上。要么所有节点都更新数据,要么都不更新。始终保持所有节点数据一致。
并且在这个数据同步期间,分布式系统不能对外提供服务,否则会违背一致性(因为可能会访问到尚未同步的节点,此时读到的数据就不一致了)。
举个例子,当对节点 A 执行操作 set x = 1; 之后,x 的新值会立刻同步到所有的节点上,保证所有的节点上 x 值都被更新为 1。
1.2、可用性(Availability)
可用性(Availability):代表系统不间断地提供服务的能力。
即任何时刻对于分布式系统节点的访问都会返回成功的结果,而不会是超时或者失败。可用性强调的是一定能读到数据,至于读取到的数据是新值还是旧值都不影响,但一定要能成功访问。
1.3、分区容忍性(Partition Tolerance)
分区容忍性(Partition Tolerance):代表分布式系统在面对网络分区(Network Partition)时仍然能够正常运行的能力。网络分区是指系统中的节点之间无法互相通信或通信延迟非常高的情况。
在分布式系统中,由于网络的不可靠性和不稳定性,网络分区是常见的情况。例如,一个由多个节点组成的分布式系统可能由于网络故障、服务器故障或网络拥塞等原因导致节点之间无法彼此通信。
分区容错性的目标是使分布式系统能够在网络分区的情况下仍然保持运行和提供服务。这意味着即使网络分区发生,系统的各个节点仍然能够正常处理请求、进行数据读写操作,并向用户提供结果。
二、为什么说CAP不能同时满足
2.1、举例一
我们都听过分布式系统中 CAP 是无法同时满足的,但是很多时候都是只有一个模糊概念,所以我就从一个简单例子说起吧。
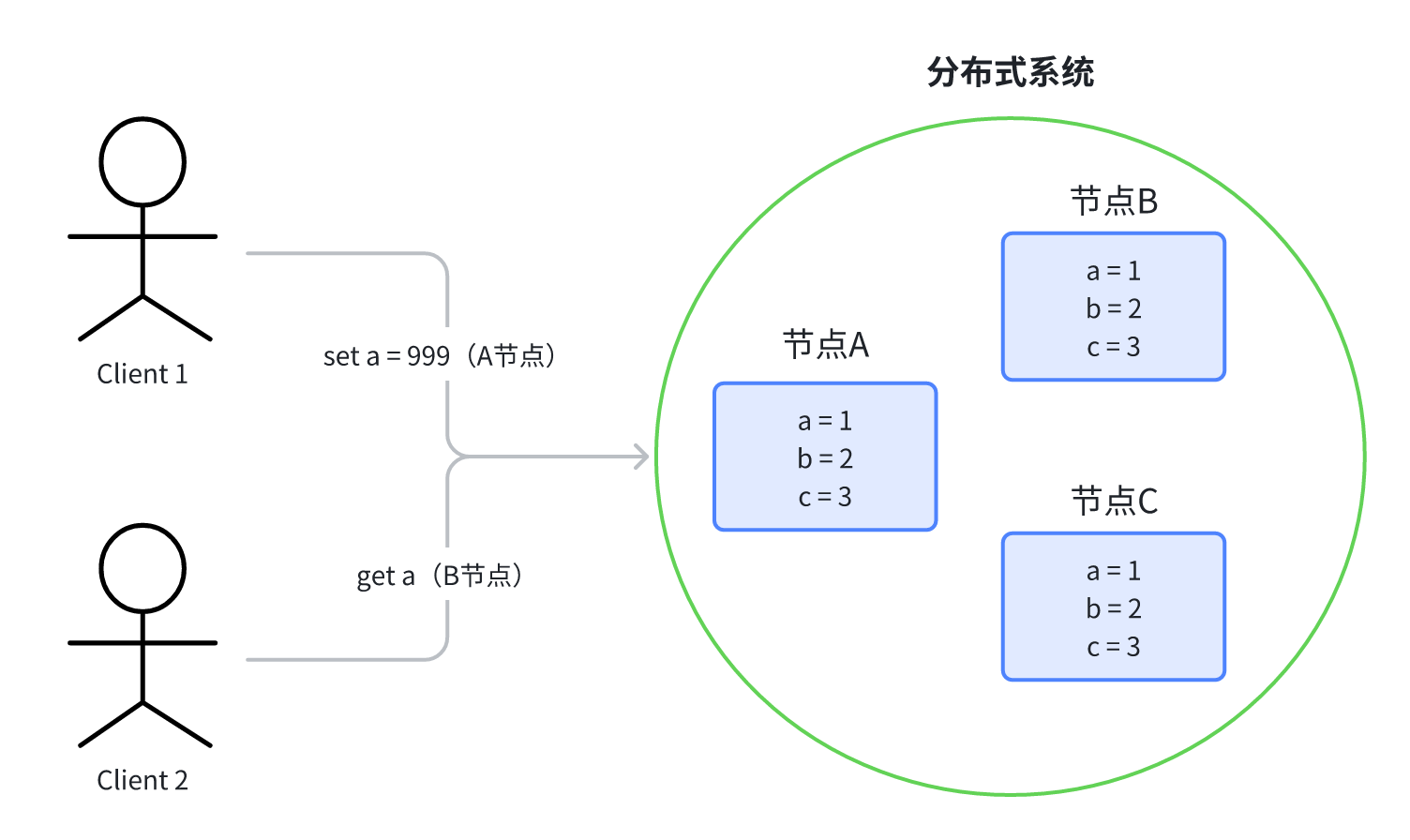
有一个很简单的程序,就存了几个键值对。我们在多台机器上都部署这个程序,整体对外提供服务,这就成了一个简单的分布式系统。每一个运行的程序称为一个节点,如图所示:
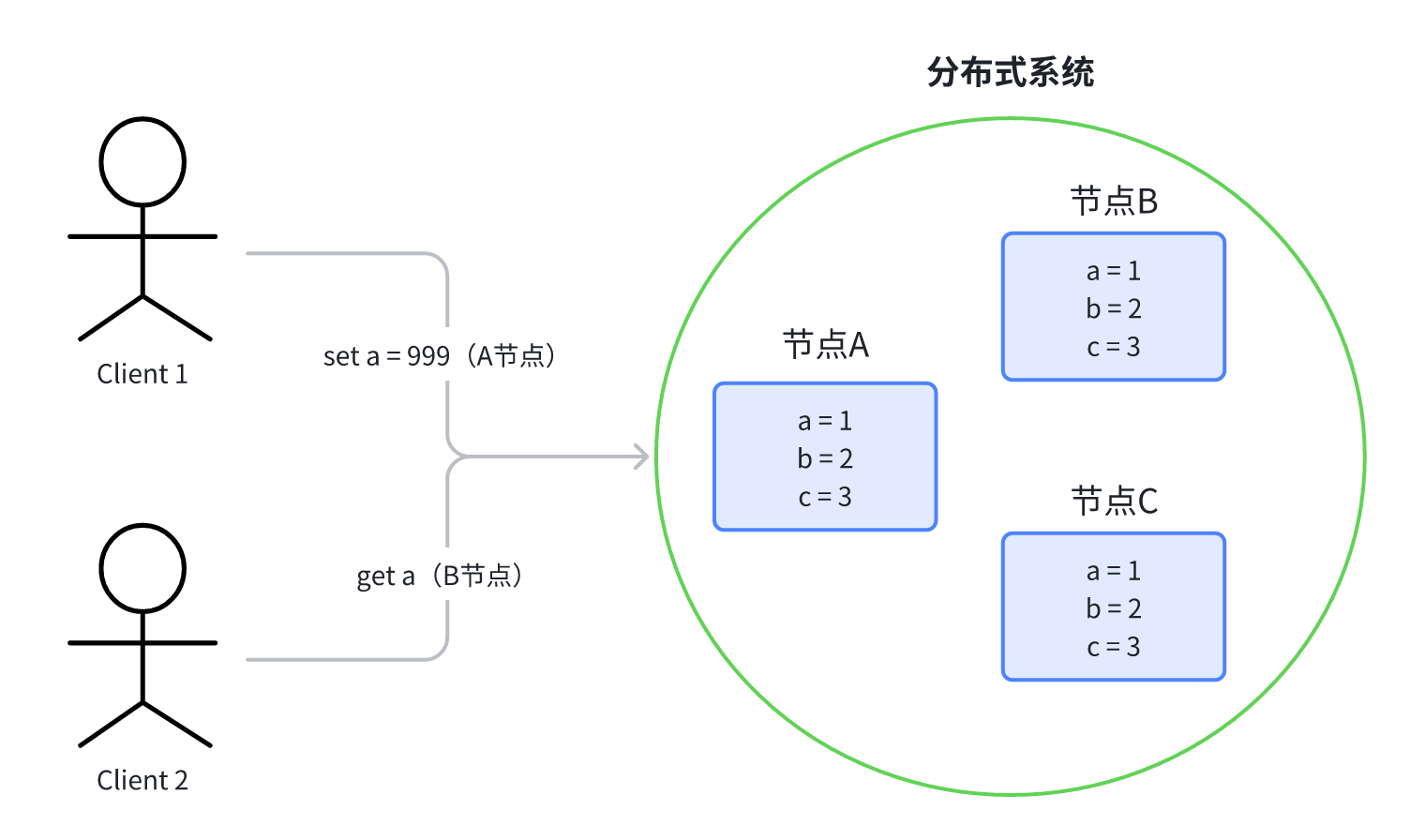
此时,某个客户端 Client1 连接了节点 A,向节点 A 发起请求: SET a = 999;
然后某个客户端 Client2 连接了节点 B,发送请求:GET a; 立马读取 a 的值。
先假设现在我们要满足 Consistency 一致性。前面提过,需要保证:当在分布式系统更新一个节点的数据时候,分布式系统会立马把这个数据同步到所有的节点上。要么所有节点都更新数据,要么都不更新。始终保持所有节点数据一致。
怎么保证这一点呢?有两个方案:
方案一:数据全部都只存放在一个节点上。其他节点全部从这个节点上读取数据。
很容易理解,所有数据都在一个节点上,那么就根本不需要 "把数据同步到其他节点" 这一步操作了,其他所有节点读写数据请求都会被转发到这个节点上来执行。所以它一定满足Consistency一致性。
在这个例子中即只有节点 A保存了所有数据,其他节点数据全是空的,Client2的请求会被转发到节点 A 上,因此得到的a 都是 999。一致性得到保证。
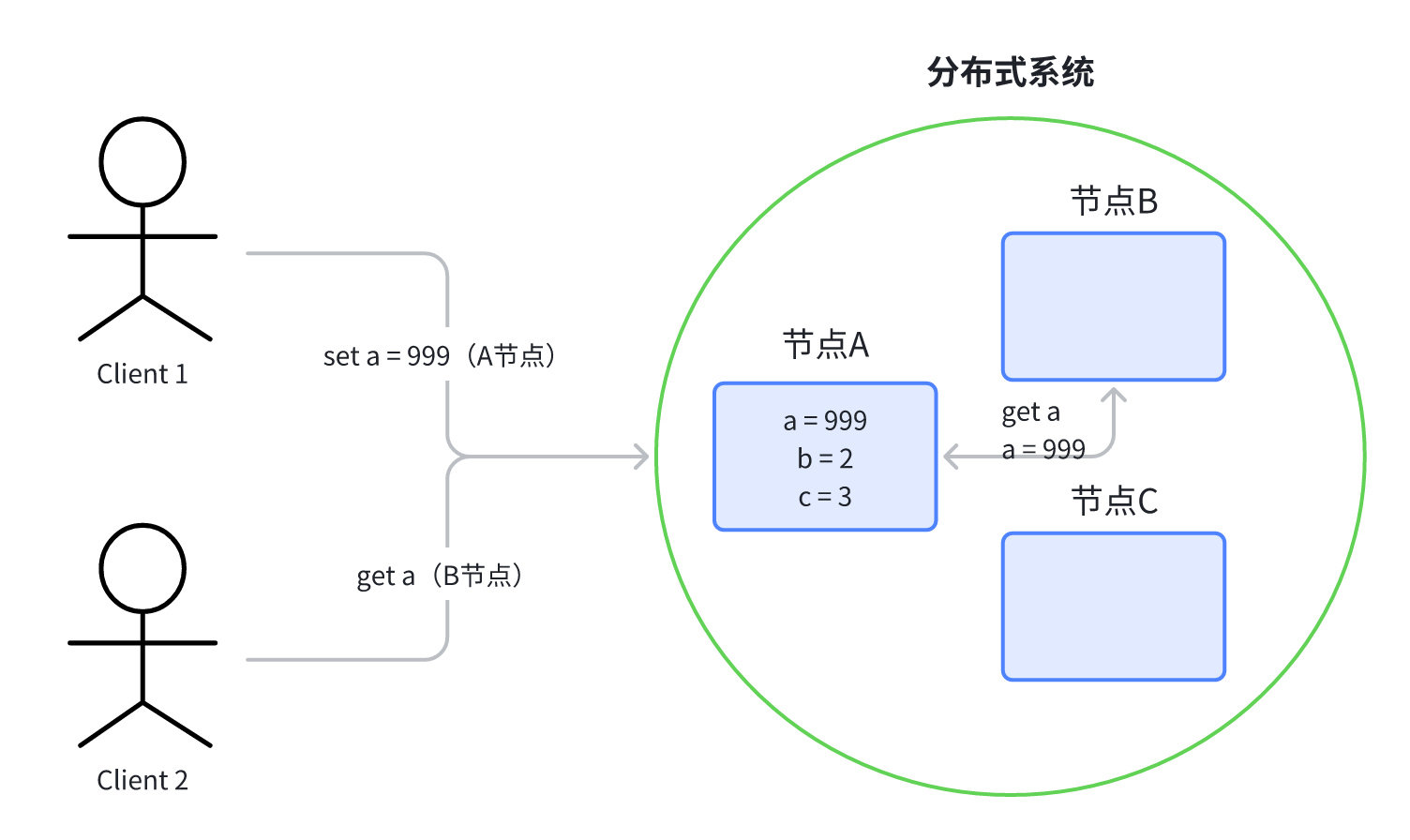
另外,由于只有一份数据,没有数据同步这一步骤,因此分布式系统在任何时间都是能对外提供服务的。下一个请求能够立马得到成功的响应。所以 Availability 可用性 也是满足的。
然而,这个系统满足 Partition-tolerance 分区容错性 吗? 遗憾的是并不满足:
很简单,因为数据全部存在节点 A 上。假设节点 B 与节点 A 的网络通信因为某种原因中断了(这是很有可能的),此时发生分区。节点 B 就无法对外提供服务了,因为他无法从节点 A 拿到数据。这违背了分区容错性的定义。所以不满足分区容错性。
综上,这个系统满足 Consistency 一致性 和 Availability 可用性,但是不满足 Partition-tolerance 分区容错性。这属于 CA。
方案二:每个节点都存放数据。
在这种方案下,要保证一致性,那么必须要将数据修改立刻同步到每一个节点。然而同步数据总得需要时间,在这个时间段内,分布式系统不能对外响应,否则会违背一致性。
当在节点 A 执行 SET a = 999 的操作后,节点 A 需要将这个操作同步到其他的节点上,保证数据的一致性。
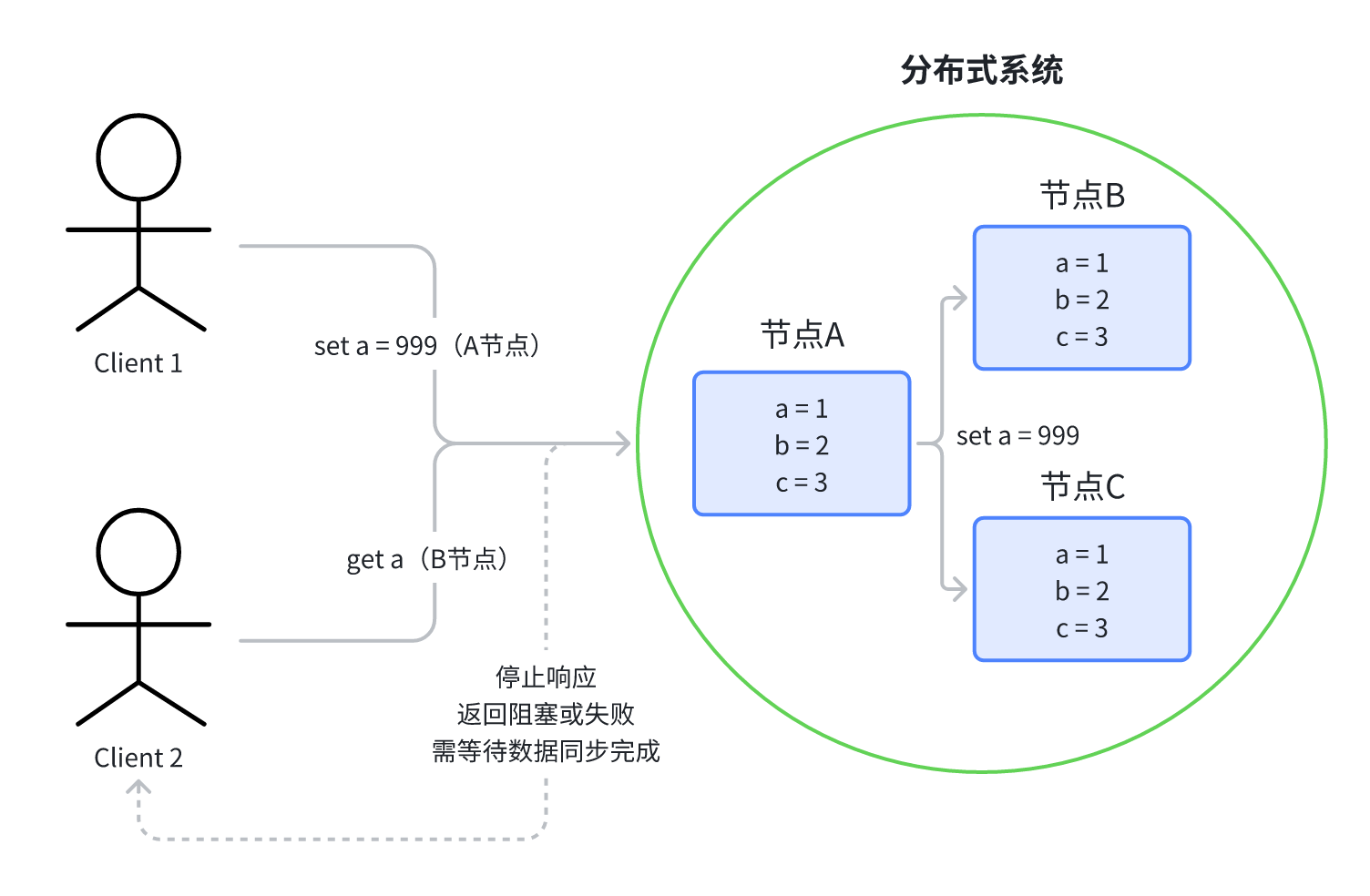
Consistency 一致性 满足之后,每个节点都是完全相同的数据备份。此时就算某个节点 A 与其他节点的通信中断,此时产生了两个分区 单独的节点A 是一个分区, 其他所有节点 是另外一个分区。但是这两个分区都有完整的数据,因此都可以对外提供服务。也就是说满足了 Partition-tolerance 分区容错性。
那可用性满足吗?并不。
在节点数据同步的过程中,整个分布式系统不能对外提供服务。因此在这个过程中的请求都无法得到响应,所以 Availability 可用性 无法满足。Client2 的请求会超时,而不是立马返回成功,因此可用性不成立。
综上,这个属于 CP。
另外,假设我不选择 Consistency 一致性 的时候,能同时满足 Availability 可用性 和 Partition-tolerance 分区容错性 吗?
可以。 因为不需要满足一致性了,实际上每个节点的数据都有自己的副本,但是这些副本的值并不一定完全相同,因为没有数据同步。对于 Client1 来说 GET a 得到的是 999. 而对于 Client2 来说 GET a 是 1。
此时就算发生网络分区,每个节点都还是能对外服务的。所以满足 Partition-tolerance 分区容错性。
而且任一时刻的请求也能正常得到响应,因为没有数据同步的过程,自然任何时候都能处理请求了,所以也满足 Availability 可用性。 这个就是 AP。
至此,我们已经可以得到结论。分布式系统中 CAP 三者是不能完全同时满足的,只能够3选2了。
通常,在分布式系统中 Partition-tolerance 分区容错性 是我们不得不选择的。 很容易理解,不选择分区容错性,就等于数据只放在一个节点A上。那这个分布式系统的意义好像也不大,搞来搞去鸡蛋还是放在一个篮子里了。这个节点 A一旦挂了整个系统毫无疑问直接挂掉,这对生产环境来说通常是难以接受的。
2.2、举例二
单纯只列概念,CAP 是比较抽象的。假设 蔚来商城 的服务拓扑如图所示,一个来自最终用户的交易请求,将交由账号、商家和仓库服务集群中某一个节点来完成响应:
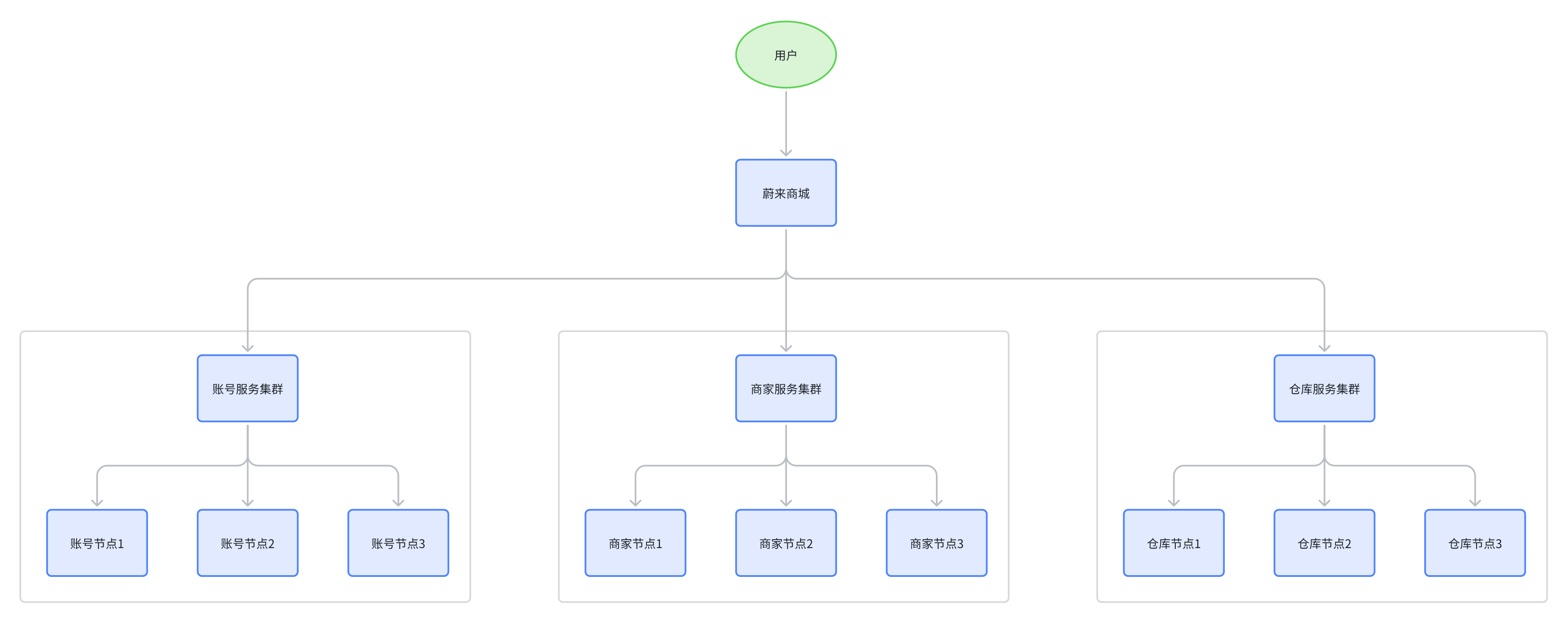
在这套系统中,每一个单独的服务节点都有自己的数据库,假设某次交易请求分别由“账号节点 1”、“商家节点 2”、“仓库节点 N”联合进行响应。当用户购买一件价值 100 元的商品后,账号节点 1 首先应给该用户账号扣减 100 元货款,它在自己数据库扣减 100 元很容易,但它还要把这次交易变动告知本集群的节点 2 到节点 N,并要确保能正确变更商家和仓库集群其他账号节点中的关联数据,此时将面临以下可能的情况。
-
如果该变动信息没有及时同步给其他账号节点,将导致有可能发生用户购买另一商品时,被分配给到另一个节点处理,由于看到账号上有不正确的余额而错误地发生了原本无法进行的交易,此为一致性问题。
-
如果由于要把该变动信息同步给其他账号节点,必须暂时停止对该用户的交易服务,直至数据同步一致后再重新恢复,将可能导致用户在下一次购买商品时,因系统暂时无法提供服务而被拒绝交易,此为可用性问题。
-
如果由于账号服务集群中某一部分节点,因出现网络问题,无法正常与另一部分节点交换账号变动信息,此时服务集群中无论哪一部分节点对外提供的服务都可能是不正确的,整个集群能否承受由于部分节点之间的连接中断而仍然能够正确地提供服务,此为分区容忍性。
以上还仅仅涉及了账号服务集群自身的 CAP 问题,对于整个 Fenix's Bookstore 站点来说,它更是面临着来自于账号、商家和仓库服务集群带来的 CAP 问题,譬如,用户账号扣款后,由于未及时通知仓库服务中的全部节点,导致另一次交易中看到仓库里有不正确的库存数据而发生超售。又譬如因涉及仓库中某个商品的交易正在进行,为了同步用户、商家和仓库的交易变动,而暂时锁定该商品的交易服务,导致了的可用性问题,等等。
三、舍弃 C、A、P 时所带来的不同影响
由于 CAP 定理已有严格的证明,来分析如果舍弃 C、A、P 时所带来的不同影响。
-
如果放弃分区容忍性(CA without P),意味着我们将假设节点之间通信永远是可靠的。永远可靠的通信在分布式系统中必定不成立的,这不是你想不想的问题,而是只要用到网络来共享数据,分区现象就会始终存在。在现实中,最容易找到放弃分区容忍性的例子便是传统的关系数据库集群,这样的集群虽然依然采用由网络连接的多个节点来协同工作,但数据却不是通过网络来实现共享的。
-
如果放弃可用性(CP without A),意味着我们将假设一旦网络发生分区,节点之间的信息同步时间可以无限制地延长,此时,问题相当于退化到前面“全局事务”中讨论的一个系统使用多个数据源的场景之中,我们可以通过 2PC/3PC 等手段,同时获得分区容忍性和一致性。
-
如果放弃一致性(AP without C),意味着我们将假设一旦发生分区,节点之间所提供的数据可能不一致。选择放弃一致性的 AP 系统目前是设计分布式系统的主流选择,因为 P 是分布式网络的天然属性,你再不想要也无法丢弃;而 A 通常是建设分布式的目的,如果可用性随着节点数量增加反而降低的话,很多分布式系统可能就失去了存在的价值,除非银行、证券这些涉及金钱交易的服务,宁可中断也不能出错,否则多数系统是不能容忍节点越多可用性反而越低的。目前大多数 NoSQL 库和支持分布式的缓存框架都是 AP 系统,以 Redis 集群为例,如果某个 Redis 节点出现网络分区,那仍不妨碍各个节点以自己本地存储的数据对外提供缓存服务,但这时有可能出现请求分配到不同节点时返回给客户端的是不一致的数据。
到这里,不知道你是否对“选择放弃一致性的 AP 系统目前是设计分布式系统的主流选择”这个结论感到一丝无奈,“事务”原本的目的就是获得“一致性”,而在分布式环境中,“一致性”却不得不成为通常被牺牲、被放弃的那一项属性。但无论如何,我们建设信息系统,终究还是要确保操作结果至少在最终交付的时候是正确的,这句话的意思是允许数据在中间过程出错(不一致),但应该在输出时被修正过来。
总之适合业务场景的方案才是最好的方案。
相关文章:

【分布式】CAP理论详解
一、CAP理论概述 在分布式系统中,CAP是指一组原则,它们描述了在网络分区(Partition)时,分布式系统能够提供的保证。CAP代表Consistency(一致性)、Availability(可用性)和…...
AI歌姬,C位出道,基于PaddleHub/Diffsinger实现音频歌声合成操作(Python3.10)
懂乐理的音乐专业人士可以通过写乐谱并通过乐器演奏来展示他们的音乐创意和构思,但不识谱的素人如果也想跨界玩儿音乐,那么门槛儿就有点高了。但随着人工智能技术的快速迭代,现在任何一个人都可以成为“创作型歌手”,即自主创作并…...

ZooKeeper基本知识
1.什么是ZooKeeper ZooKeeper是一个开源的分布式协调服务,它提供了一个高性能、高可靠的分布式协调基础,用于构建分布式系统。 具体来说,ZooKeeper通常用于以下几个方面: 配置管理:分布式系统通常需要集中管理配置信…...
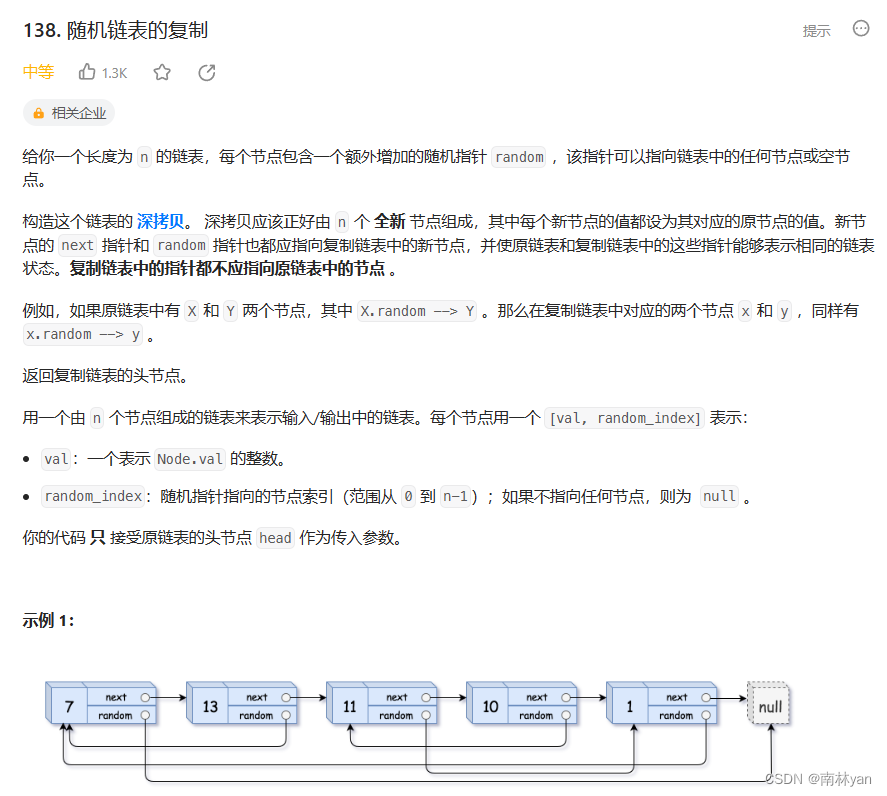
leetcode:138. 随机链表的复制
一、题目: 138. 随机链表的复制 - 力扣(LeetCode) 函数原型: struct Node* copyRandomList(struct Node* head) 二、思路 本题是给出一个单链表,单链表的每个结点还额外有一个随机指针,随机指向其他结点&am…...
)
SpringBoot 全局异常之参数校验(1)
文章目录 前言背景依赖校验类型@NotBlank、@NotNull和@NotEmpty的区别@Valid和@Validated区别异常处理方式一 @RequestParam全局异常处理(ConstraintViolationException)请求示例方式二 @RequestBody(推荐)全局异常处理(MethodArgumentNotValidException)请求示例方式三(…...
QT windows与linux之间sokcet通信中文乱码问题解决方法
QT windows与linux之间sokcet通信中文乱码问题解决方法 linux发送与接收都转码utf-8: tcpClient ->write( send_msg.toUtf8());//解决乱码,发送转码 接收: QByteArray buffer tcpClient->readAll(); if(!buffer.isEmpty()) { // ui->plain…...

Java实现DXF文件转换成PDF
代码实现 public static void dxfToPdf(){// 加载DXF文件String inputFile "input.dxf";CadImage cadImage (CadImage) Image.load(inputFile);// 设置PDF输出选项PdfOptions pdfOptions new PdfOptions();pdfOptions.setPageWidth(200);pdfOptions.setPageHeigh…...

揭秘Vue中的nextTick:异步更新队列背后的技术原理大揭秘!
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 ⭐ 专栏简介 📘 文章引言 一、N…...

PHP使用文件缓存实现html静态化
<?php // 动态生成的内容 $content "<html><body><h1>time:".date("Y-m-d H:i:s")."</h1></body></html>"; // 静态文件保存路径和文件名 $staticFilePath "file.html"; if(file_exists($s…...
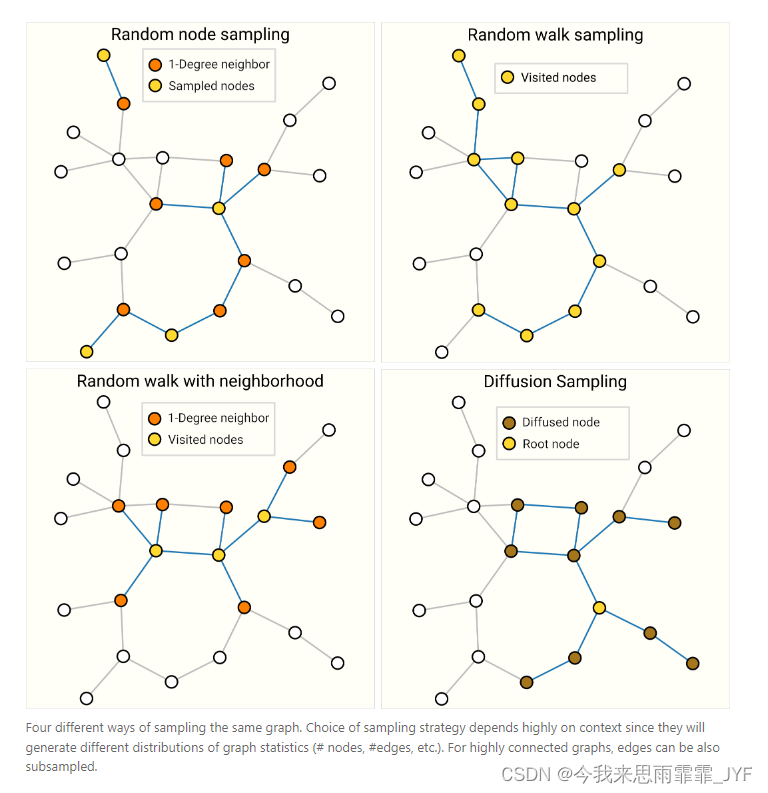
A Gentle Introduction to Graph Neural Networks
A Gentle Introduction to Graph Neural Networks----《图神经网络入门》 图神经网络信息传递积累 图在我们身边随处可见,现实世界中的物体通常是根据它们与其他事物的联系来定义的。一组物体以及它们之间的联系可以很自然地用图来表示。十多年来,研究人…...
详解[ZJCTF 2019]NiZhuanSiWei 1(PHP两种伪协议、PHP反序列化漏洞、PHP强比较)还有那道题有这么经典?
题目环境: <?php $text $_GET["text"]; $file $_GET["file"]; $password $_GET["password"]; if(isset($text)&&(file_get_contents($text,r)"welcome to the zjctf")){echo "<br><h1>&…...

bazel build使用【未完】
1. install install的作用:将生成的目标、文件复制到指定的安装目录中,可以是可执行文件、库文件、 配置文件等 若有一个c可执行文件,可以使用install将其安装到标准的可执行路径中,以便于直接运行,而无需指定完整的文…...
11-13 /11-14代理模式 AOP
调用者 代理对象 目标对象 代理对象除了可以完成核心任务,还可以增强其他任务,无感的增强 代理模式目的: 不改变目标对象的目标方法的前提,去增强目标方法 分为:静态代理,动态代理 静态代理 有对象->前提需要有一个类,那么我们可以事先写好一个类&a…...
Ubuntu 创建并发布 Django 项目
Ubuntu 创建并发布 Django 项目 升级操作系统和软件 sudo apt updatesudo apt -y dist-upgrade 安装 python3-pip sudo apt -y install python3-pip安装 django pip install -i https://pypi.tuna.tsinghua.edu.cn/simple djangosudo apt -y install python3-django创建 dj…...

SQL Server进阶知识
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开心好久好久😎 📚系列专栏:Java全栈,…...

TFHEpp 使用记录
TFHEpp 使用记录 使用HE3DB错误randen 使用 需要使用 编译器gcc > 10 (unicode 编码) sudo apt-get install -y build-essential g-10 apt-utils ca-certificates git cmake libgmp-dev libfftw3-devgit clone https://github.com/virtualsecureplatform/TFHEpp cd TFHEp…...
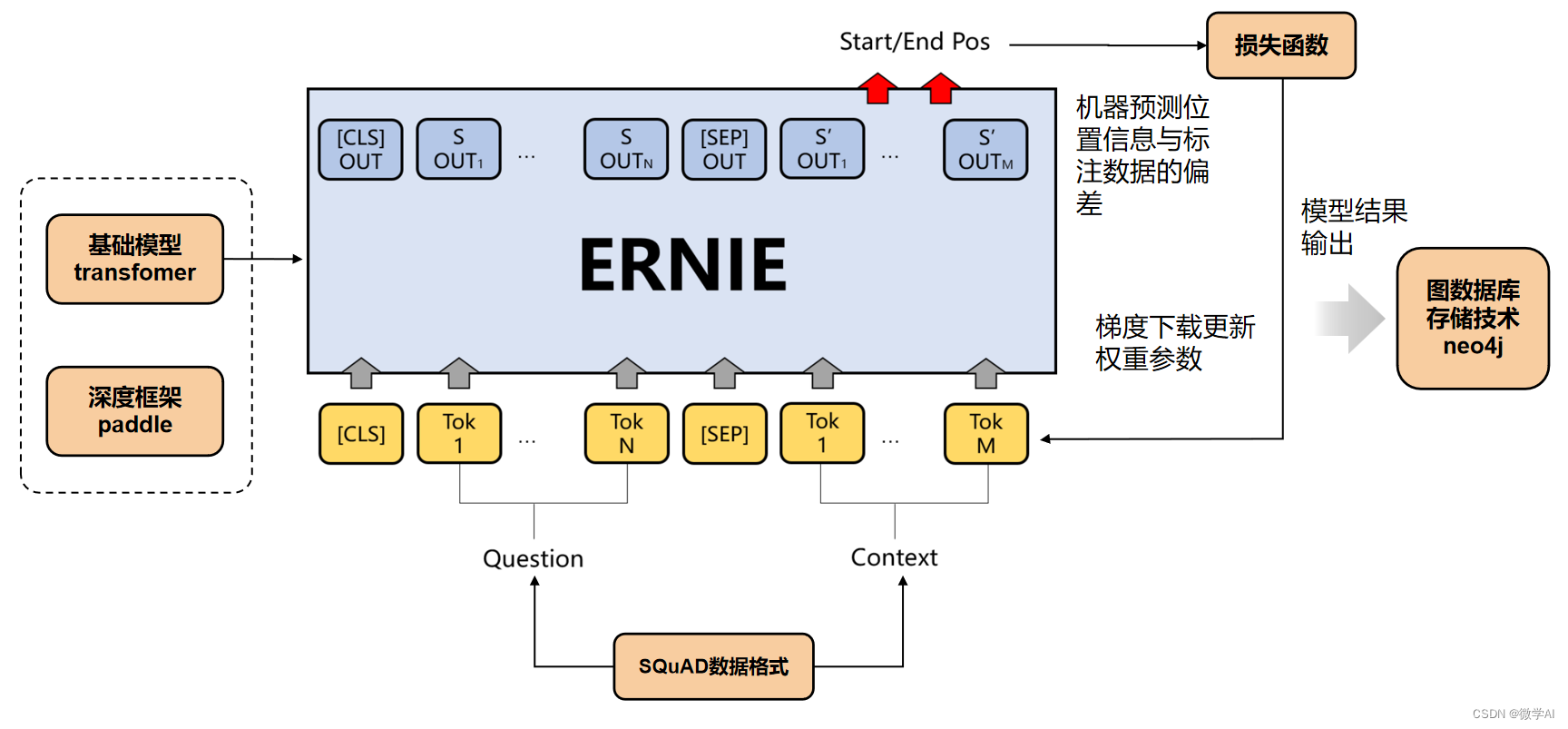
大模型的实践应用6-百度文心一言的基础模型ERNIE的详细介绍,与BERT模型的比较说明
大家好,我是微学AI,今天给大家讲一下大模型的实践应用6-百度文心一言的基础模型ERNIE的详细介绍,与BERT模型的比较说明。在大规模语料库上预先训练的BERT等神经语言表示模型可以很好地从纯文本中捕获丰富的语义模式,并通过微调的方式一致地提高各种NLP任务的性能。然而,现…...

vue:如何把后端传过来的数组的其中一个对象加入新的属性
加入我们是更改数组中的第一个对象,在vue中可以使用$set方法将属性插入到第一个对象中作为属性。 Script部分: <script>export default {data() {return {boxes: [//模拟后端传过来的数组{id:1,name:张三},{id:2,name:李四},{id:3,name:王五},{i…...

数据库数据恢复—MSSQL报错“附加数据库错误823”如何恢复数据?
数据库故障&分析: MSSQL Server数据库比较常见的报错是“附加数据库错误823”。如果数据库有备份,只需要还原备份即可;如果无备份或者备份不可用,则需要使用专业的数据恢复手段去恢复数据。 MSSQL Server数据库出现“823”的报…...

如何使用 Java 设计一个简单的成绩计算程序
简介 本文将介绍如何使用 Java 设计一个简单的成绩计算程序。该程序可以读取学生的成绩并计算出平均分、最高分和最低分等。通过这个例子,我们将展示如何使用面向对象的思想和一些常用的 Java 功能来解决实际问题。 需求分析 在开始编写程序之前,我们…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
